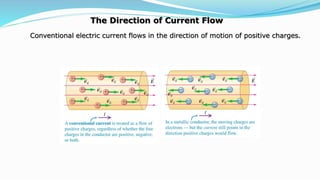
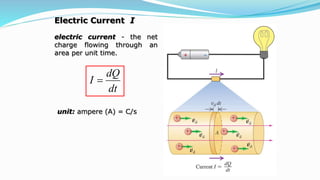
This document discusses electric current and its characteristics. It defines electric current as the net flow of electric charge through an area per unit time. It also defines current density as the amount of electric charge flowing per unit area of a conductor. The document explains that electric current occurs when an electric field is established in a conductor, causing electric charges to drift through the material. It also discusses resistivity, resistance, and how both increase with temperature. Finally, it defines electromotive force and distinguishes it from terminal voltage.

2. Electric Current: Motion of Electric Charges
• If there is no electric field in a conductor, there is no electric current.1
1If there is no current, it does not mean that all electric charges are at rest. Free electrons
move randomly at high speeds (in the order of 106 m/s)
• If an electric field is established in the conductor, an electric force, F = qE,
acts on the charges and accelerates them.2
2The electric charges actually move very slowly because they frequently collide with the particles
of the material. The drift velocity vd of the charges is in the order of 10-4 m/s.
• The electric force does work on the charges resulting in an increase in the
charges’ kinetic energy.3
3Instead of accelerating the charges to high speeds, most of the resulting kinetic energy are
transferred to the particles of the material – the temperature of the material increases.

3. The Direction of Current Flow
Conventional electric current flows in the direction of motion of positive charges.

4. Electric Current I
electric current - the net
charge flowing through an
area per unit time.
unit: ampere (A) = C/s
dt
dQ
I 

5. Current Density J
Current density is the amount of electric charges flowing
per unit area of a conductor.
dt
nAvd
The number of particles within
the unit volume dV = Avd dt is
If each particle has a charge
q, the charge in the unit
volume is
 
dt
nAv
q
dQ d

d
nqAv
dt
dQ
I 
 d
nqv
A
I
J 
 unit: A/m2

6. Resistivity 
In a conductor, the current density J is directly
proportional to the electric field E.
J
E


Ohm’s Law: In a conductor, the current density J is directly
proportional to the electric field E.4
where  is a constant called the
resistivity of the material in m.
4valid for ohmic materials.

7. Resistivities at Room Temperature (20oC)

8. Resistivity and Temperature
The resistivity of a metallic conductor increases with
temperature. Over a small range of temperature (about
100Co),
   
 
o
o T
T
T 

 

 1
where: o - resistivity at room temperature To
 - resistivity at temperature T
 - temperature coefficient
Temperature Coefficients

9. Resistance
Consider a conductor of uniform cross-section A, length
L and carrying a constant current.
L
V
E 
The electric field E and current
density J are uniform.
Recall Ohm’s Law: J
E 

A
I
L
V


A
L
I
V


I
V
R 
A
L
R 

A
I
J 

10. Resistance and Temperature
The resistance R of a metallic conductor increases with
temperature. Over a small range of temperature (about
100Co),
   
 
o
o T
T
R
T
R 

 
1
where: Ro - resistance at room temperature To
R - resistance at temperature T
 - temperature coefficient

11. Electromotive Force  and Terminal Voltage
In a complete circuit a source of emf  is required for
steady flow of current.
emf – the voltage across the source when not connected to a
closed circuit.
terminal voltage Vab – the voltage across the terminals of
the source when connected in a closed circuit.
internal resistance r – the resistance inside the source of
emf.