Tài liệu này trình bày các kiến thức cơ bản về thống kê và khai phá dữ liệu, chủ yếu sử dụng Excel để tính toán các chỉ số thống kê như trung bình, phương sai và độ lệch chuẩn. Nó cũng giải thích mối tương quan giữa các biến và ứng dụng của hồi quy tuyến tính đơn giản để phân tích mối quan hệ giữa các dữ liệu. Tài liệu cung cấp hướng dẫn từng bước để tính toán và biểu diễn dữ liệu bằng biểu đồ trong Excel.


























































![59
Biểu đồ tương tự như biểu đồ đã hoàn thành trong Excel (không có tiêu đề).
Python có khả năng tạo ra nhiều loại đồ thị tuyệt vời.
3. Hồi quy tuyến tính đơn giản
Ví dụ 1.5.1. đã giới thiệu hồi quy tuyến tính đơn giản, điều này sẽ được tạo
lại bằng Python.
3.1. Ví dụ về hồi quy tuyến tính đơn giản
Chúng ta muốn kiểm tra xem có mối quan hệ giữa độ dày của miếng bọt
biển và độ thấm hút chất lỏng của nó hay không. Chúng tôi đã thiết kế một thí
nghiệm với các mức độ dày khác nhau của bọt biển, với lượng chất lỏng được hấp
thụ. Kết quả được ghi trong bảng 4.3.
Bảng 4.3: Dữ liệu hồi quy tuyến tính đơn giản.
Trong Python, các bước sau sẽ được tiến hành: Tạo mảng, trong cuốn sách
này, chúng tôi sẽ định nghĩa mảng là một biến có thể lưu trữ danh sách các giá trị.
Tạo hồi quy tuyến tính đơn giản; Tạo đồ thị có trục và tiêu đề được gắn nhãn
Chương trình 4-12 dưới đây: Tạo mảng của chúng ta.
np.array, nói với Python rằng chúng ta muốn tạo mảng bằng cách sử dụng
các số liệu bên trong ([…]).
Bây giờ, chúng ta có hai mảng: đầu vào x và đầu ra y. Để hồi quy hoạt động
trong Python, chúng ta cần sửa đổi x thành hai chiều, một cột, nhưng nhiều hàng.
Đó là lý do tại sao chúng ta cần định hình lại lệnh ((- 1,1)). Mảng cho phép chúng
ta thao tác dữ liệu dễ dàng hơn.](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-59-320.jpg)











![71
Từ lệnh info (), chúng ta có thể thấy rằng mẫu khung dữ liệu có:
+ 13508 obs (hàng);
+ 16 biến (cột);
+ Tên của tất cả các biến (phân biệt chữ hoa chữ thường);
+ Các biến là số nguyên (int64) hoặc number (float64).
Điều này đã cho chúng ta hiểu rõ hơn về dữ liệu mà lệnh head () không thể
truyền tải.
5.3 Thao tác dữ liệu
Có thể sửa đổi dữ liệu và chỉ chọn các giá trị cụ thể tạo thành một cột là kỹ
năng quan trọng đối với bất kỳ nhà phân tích / nhà khoa học quyết định nào.
5.3.1. Equal to
Nếu chúng ta muốn tạo một khung dữ liệu mới chỉ chứa những khách hàng
đã phá sản (target = 1), thì chúng ta sẽ viết một chương trình nhỏ. Trong Python,
nếu muốn một biến có giá trị bằng nhau, thì chúng ta sẽ sử dụng hai dấu bằng ‘==’.
Chương trình 5-4: Equal to
Mã đã được chia nhỏ như sau:
+ targ1 - tên của khung dữ liệu mới được tạo;
+ mẫu - tên của khung dữ liệu mà chúng ta sẽ sử dụng;
+ [sample $ target - thông báo cho Python biết khung dữ liệu và biến chúng
ta muốn sử dụng;
+ == 1 - như đã đề cập trước đây, trong Python, chúng ta sẽ sử dụng '==' có
nghĩa là bằng;
+ ] - chỉ định phần cuối của lệnh.
Trong Python, tên cột và khung dữ liệu phân biệt chữ hoa chữ thường, do
đó 'Target' sẽ không hoạt động, ngược lại ' target 'không. Lệnh info () đã được đưa
vào để hoàn thiện, nhưng chúng ta không cần phải chạy nó. Nếu chúng ta nhìn vào](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-71-320.jpg)




![76
Chương trình 5-10: Thao tác dữ liệu biến ký tự
1) char1 = bosh [bosh.boom == "EXAMPLE"]:
a. Chúng ta có thể sử dụng dấu ngoặc kép hoặc đơn, nhưng bạn phải nhớ sử
dụng chúng và không trộn lẫn chúng, v.d. “EXAMPLE’ sẽ không hoạt động.
2) Tương tự như số 1, nhưng sử dụng số khác.
3) Một lần nữa, như được hiển thị trước đó với phiên bản số, nhưng các từ
được bao quanh bởi dấu ngoặc kép.
4) Nhiều hoặc câu lệnh:
a. Điều này chứng tỏ rằng chúng ta có thể sử dụng nhiều câu lệnh ‘or’.
5) Điều này sử dụng một cách rút gọn từ việc viết ra cùng một biến nhiều
lần. Trong trường hợp này, chúng ta có thể sử dụng lệnh
‘isin’, lệnh này cung cấp cho chúng ta kết quả tương tự
như trong 5.
Hình 5.8 dưới đây, trình bày kết quả sử dụng các
biến đặc trưng:
Câu lệnh isin có thể được sử dụng cho các giá trị
số cũng như đặc trưng. Khi xử lý các biến đặc trưng, phải
nhớ rằng nó có phân biệt chữ hoa chữ thường. Chẳng
hạn: từ ví dụ trước, char1 = bosh [bosh.boom ==
"EXAMpLE"] sẽ không hoạt động.](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-76-320.jpg)
![77
5.4 Thao tác với khung dữ liệu trong Python
5.4.1 Cập nhật giá trị null
Khi làm việc với dữ liệu, nó hiếm khi sẵn sàng để sử dụng (sạch). Khi đó,
chúng ta sẽ làm sạch dữ liệu để làm cho nó có thể sử dụng được. Từ hình 5.2, quan
sát thấy rằng có một số giá trị bị thiếu cho CCJ_go Government và CCJ_private.
(NA). Ba nguyên nhân phổ biến của việc thiếu giá trị là:
Không xác định;
Tệp dữ liệu được nhập không chính xác;
Tỷ lệ đối sánh không thành công.
Các biến CCJ_go Government và CCJ_private chứa các giá trị bị thiếu vì
chúng chưa bao giờ có bất kỳ CCJ nào. Đối với các cột này, chúng ta thay thế các
giá trị bị thiếu bằng 0. Đoạn mã dưới đây minh họa cách nó được hoàn thành.
Đoạn mã trên:
+ sample['CCJ_government'] =
chỉ định khung dữ liệu và cột chúng tôi đang sửa đổi / tạo.
+ sample['CCJ_government'].
chỉ định khung dữ liệu và cột mà chúng tôi đang điều tra.
+ fillna(0)
Thay đổi NA thành không.
Điều này sau đó được lặp lại cho CCJ_private.](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-77-320.jpg)
![78
Kiểm tra kết quả bằng cách nhấp đúp vào mẫu.
5.4.2 Tạo cột mới
Khả năng tạo cột mới là kỹ năng quan trọng đối với nhà phân tích. Đôi khi,
chúng ta có thể muốn thêm một giá trị duy nhất vào khung dữ liệu hoặc tạo một
cột mới dựa trên thông tin đã có trong khung dữ liệu. Ví dụ đầu tiên là tạo một cột
mới với giá trị 1 được gọi là số đếm, trong mẫu khung dữ liệu.
Chương trình 5-12: Tạo một cột mới.
Đây là một trong những tình huống mà việc viết ra những gì chúng ta sẽ làm
dài hơn bản thân mã. Chỉ cần nhớ ghi khung dữ liệu trước, sau đó là tên cột với
[‘..’] Như thường lệ, hãy nhớ chạy mã. Nếu chúng ta muốn thêm cột ngày vào
khung dữ liệu của mình thì chúng ta chỉ cần sử dụng pandas library và to_datetime
command.
Phần tiếp theo liên quan đến việc tạo một biến (cột) mới dựa trên các giá trị
từ các biến khác nhau trong khung dữ liệu, mẫu. Một cột mới có tên là "totalbank"
sẽ được tạo, cột này tổng hợp tổng số dư ngân hàng trong khung dữ liệu.](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-78-320.jpg)

![80
Cột mới của chúng ta có lưu trữ ‘Inf’ bên trong nó, cũng như nan. Điều này
có nghĩa là vô hạn, vì chúng ta đã chia một số cho không. Một cách đơn giản để
giải quyết vấn đề này là chỉ tính tỷ lệ này khi số tiền tiết kiệm được không bằng 0.
Điều này dẫn đến việc sử dụng lệnh where. Thay vì đưa ra lý thuyết, cuốn sách
này sẽ chứng minh cách chúng được sử dụng với một ví dụ.
Program 5-16: Sử dụng lệnh
+ sample['amtowesav'] <-
This is the name of our new column within the data frame.
+ np.where(sample.savings !=0, sample.amount_owed / sample.savings, 0)
np.where – lệnh mới, hoạt động rất giống với lệnh Excel 'IF’;
savings != 0, - thông báo cho Python biết rằng bất cứ khi nào lưu không
bằng 0, thì hãy làm như sau:
sample.amount_owed / sample.savings - tính toán chúng tôi muốn đã
hoàn thành;
0)) – tất cả where savings không bằng 0, thì đặt 0 vào cột ‘amtowesav’.
Tiếp theo là dấu ngoặc.](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-80-320.jpg)
![81
Từ phần trên, chúng ta có thể thấy rằng ‘amtowesav’ có một chuỗi dài các
số thập phân. Chỉ để hoàn chỉnh, nhưng không cần thiết, chúng ta có thể làm tròn
con số này thành một chữ số thập phân.
Chương trình 5-17: Làm tròn số
Nếu muốn có 3 chữ số thập phân, thì chỉ cần thay thế ‘1’ bằng ‘3’. Chỉ là
một lưu ý cuối cùng về biến mới. Phần tiếp theo yêu cầu tạo một cột mới được gọi
là bảng lương, sử dụng các giá trị trong cột tiền lương.
+ sample['wageband'] <
Yêu cầu Python tạo một cột mới có tên là wageband trong khung dữ liệu.
+ sample np.where(
Lệnh chỉ định tiêu chí của cột mới dựa trên dữ liệu có sẵn.
+ sample.wages<100, 'low', Nếu mức lương thấp hơn 100, thì đặt "low"
trong cột mới " wageband". Các dấu phẩy ngược sẽ không xuất hiện trong cột.
+ np.where(sample.wages<1000, 'medium',
Nếu tiền lương dưới 1000, thì hãy đặt 'medium'. Lưu ý rằng nó sẽ không
ghi đè quy tắc đầu tiên, (dưới 100) vì nó sẽ xử lý lệnh này theo thứ tự. Ngoài ra,
chúng ta chưa sử dụng dấu ngoặc đóng!](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-81-320.jpg)





![87
e. Mock_date.
Phần 4– tạo khung dữ liệu giả.
Chương trình 6-5: Chọn cột Từ đoạn mã trên
Chúng ta đã tạo một khung dữ liệu gọi là mockdata, chỉ sử dụng các cột đã
chọn (trong dấu phẩy ngược) trong [[…]]
Nếu chúng ta xem tất cả các nhiệm vụ đó cùng một lúc, thì điều đó có thể
khiến bạn nản lòng. Do khả năng chia nhỏ các nhiệm vụ thành các phần có thể
quản lý được, việc tạo khung dữ liệu cuối cùng (mockdata) của chúng ta trở nên
dễ dàng hơn. Bước tiếp theo liên quan đến việc chọn một mẫu ngẫu nhiên từ
mockdata và gọi nó là mockdata1. Lệnh được gọi là sample.
Con số (1000) thông báo cho Python biết tổng số hàng (quan sát) mà chúng
tôi yêu cầu. Trong trường hợp này, chúng ta đang yêu cầu Python cung cấp cho
1000 hàng ngẫu nhiên từ mô hình khung dữ liệu. Khung dữ liệu cuối cùng được
tạo sẽ được gọi là mocksamp.
Điều này sẽ chỉ chứa 3 cột từ mẫu khung dữ liệu:
- Id
- Wages
- Mortgage](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-87-320.jpg)
![88
Chương trình 6-6: Tạo mocksamp.
Như trước đây, việc chọn cột từ khung dữ liệu chủ yếu liên quan đến việc
đặt tên khung dữ liệu bên ngoài [[..]] và trong dấu ngoặc, liệt kê các cột muốn
trong dấu phẩy ngược được phân tách bằng dấu phẩy.
6.2 Hợp nhất các tập dữ liệu
Phần này sẽ chỉ xem xét việc kết hợp hai khung dữ liệu và sẽ tập trung vào
ba loại kết hợp khác nhau:
Full/Outer
Exclusive
Appending/concatenating
6.2.1 Full/Outer Join
Kết nối đầy đủ sử dụng tất cả dữ liệu từ cả hai tập dữ liệu và khi có dữ liệu
ở một phần chứ không phải ở phần kia, thì nó sẽ điền các giá trị này là ‘missing'.
Khi giải thích các phép nối, chúng ta có xu hướng sử dụng các vòng kết nối.
Kết hợp đầy đủ có nghĩa là chúng ta sẽ sử dụng tất cả dữ
liệu từ mocksamp và mockdata1, ngay cả khi có các quan sát
trong một tập dữ liệu và không có quan sát nào trong khác.
Sao chép và chạy mã bên dưới.
1) Lệnh ở đây là: pd.merge
a. Điều này cho Python biết bạn muốn hợp nhất các khung dữ liệu với
nhau
i. mocksamp 1. điều này cung cấp cho khung dữ liệu một bí danh được
gắn nhãn ‘x’.
ii. mockdata1](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-88-320.jpg)





![94
Phần trên cho Python biết rằng nếu target bằng 1, thì cột bị phá sản bằng
“CÓ”, còn lại đối với tất cả các hàng khác, hãy phá sản bằng “KHÔNG”. Đối với
bước 3, chúng ta sẽ tóm tắt theo nhóm.
Chương trình 7-4: Tạo một biến và khung dữ liệu mới.
We have completed simple statistics before, program7-4 takes it to the next
level
+ sum_exe.groupby(['bankrupt']).
sử dụng khung dữ liệu sum_exe
groupby(['bankrupt']). – phân đoạn các thống kê sau theo biến bankrupt .
+ sum()[["count", "CCJ_government"]]
sum() – thêm (sum) trường tiếp sau
count – Cộng tất cả số 1
CCJ-government – thêm tất cả ccj_government figures.
Lập bảng kết quả để dễ tham khảo tạo ra: Bảng 7.1: Bảng kết quả
1) bankrupt
a. Biến được phân đoạn để phân tích
2) count
a. Đây là biến được sử dụng như được chỉ định trong câu lệnh tóm tắt và
cho bạn biết số hàng / quan sát đã được sử dụng từ khung dữ liệu](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-94-320.jpg)




![99
7.4. Tạo báo cáo thông tin quản lý đơn giản (MI)
Cuối cùng, các nhà quản lý cần những số liệu sâu sắc để có thể đưa ra các
quyết định thông minh. Phần tiếp theo này sẽ mở rộng kiến thức của chúng ta, hơn
nữa để tạo ra một báo cáo đơn giản và hữu ích. Điều này sẽ đòi hỏi phải viết một
lượng mã đáng kể và tạo các khung dữ liệu mới, sử dụng các kinh nghiệm trước
đây của chúng ta được đề cập đến trong cuốn sách này.
7.4.1. Ví dụ về báo cáo MI đơn giản
Tạo một báo cáo chi tiết, theo bankruptcy và cho tất cả:
+ Tổng số người
+ Mức lương trung bình
+ Số CCJ tư nhân và chính phủ
+ Số dư ngân hàng trung bình
+ Tiết kiệm trung bình.
Trước khi đưa ra giải pháp, vui lòng tìm kèm theo một đoạn mã có liên
quan. Nếu như chúng ta muốn tóm tắt và tính toán trung bình trong một dòng mã,
sau đó chúng tôi có thể sử dụng.
Chương trình 7-8: Tổng kết và tính trung bình
+ summar1 = sum_exe7_1.groupby(['bankrupt']).
Phần này sẽ quen thuộc.
+ agg({'count':'sum', 'wages':'mean').
Trước đây, chúng ta đã sử dụng tổng bên ngoài dấu ngoặc, nhưng bằng
cách sử dụng agg, với các lệnh liên quan, chúng ta có thể tính toán tổng và giá trị
trung bình.
+ reset_index()
trong các ví dụ trước của chúng tôi, cột bankrup xuất hiện trong cột chỉ mục,
điều này khó xác định. Bằng cách sử dụng lệnh này, chúng ta sẽ có một cột được
gọi là chỉ mục.](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-99-320.jpg)













![113
+ X: tổng thu nhập hàng năm của người mua (tính bằng 1.000 giây);
+ Y: số tiền vay tín dụng mà người mua nhận được (tính bằng 1.000 giây).
Điều này rõ ràng sẽ hữu ích cho nhân viên bán hàng nếu biết cách nhiều tín
dụng mà một người mua tiềm năng có thể được thuyết phục để nộp đơn, dựa trên
kiến thức về thu nhập của họ. Trong ví dụ này, chúng ta sẽ sử dụng một thư viện
khác cho hồi quy của mình, vì nó cung cấp nhiều thống kê hơn trong kết quả của
nó.
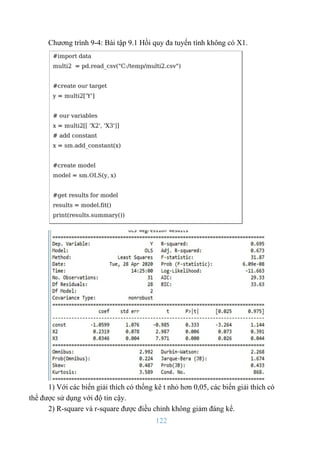
1.3.2 Giải pháp hồi quy tuyến tính trong Python
Chương trình 8-2: Hồi quy tuyến tính đơn giản - Bài tập.
1) Đầu tiên, chúng ta cần kích hoạt một thư viện mới và nhập dữ liệu
2) y = reg01 ['Y'] - từ khung dữ liệu reg01, chúng ta cần tạo một chuỗi (một
mảng) chỉ với các biến mục tiêu y
3) Giai đoạn tiếp theo liên quan đến việc tạo dữ liệu với biến mà chúng ta
muốn t sử dụng để dự đoán y. Mô hình gói trong Python không bao gồm một lệnh
chặn trong kết quả của nó, trừ khi một biến đã được tạo. Trong trường hợp này,](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-113-320.jpg)
![114
chúng tôi đã sử dụng sm.add_constant (x). Kết quả tương tự có thể đạt được với x
[‘const’] = 1.
4) Mô hình dựa trên bình phương nhỏ nhất thông thường (OLS), trong đó
sử dụng mọi thứ trong khung dữ liệu x, để dự đoán y.
5) Bằng cách gọi .fit (), chúng ta nhận được các kết quả thay đổi. Đối tượng
này nắm giữ nhiều thông tin về mô hình hồi quy.
6) In kết quả đầy đủ của chúng ta, như thể hiện trong hình 8.3.
Dưới đây là mô tả ngắn gọn về một số kết quả:
+ R-Square - R-Squared là tỷ lệ phương sai trong biến phụ thuộc có thể
được giải thích bằng các biến độc lập. R-square là thống kê để đo lường mức độ
phù hợp của mô hình với dữ liệu thực tế đã được tính toán trước đó.
+ Bình phương R được điều chỉnh - Trong nhiều mô hình hồi quy, bình
phương rsquared sẽ tăng lên khi có nhiều biến hơn được đưa vào mô hình. Đây là
sự điều chỉnh của bình phương R phạt việc bổ sung các yếu tố dự đoán không liên
quan vào mô hình. Bình phương R đã điều chỉnh được tính bằng công thức 1 - ((1
- Rsq) (N - 1) / (N - k - 1)) trong đó k là số yếu tố dự đoán.
+ F-Statistic - Mô hình bình phương trung bình chia cho Sai số bình phương
trung bình. Đây là một chỉ báo tốt về việc có mối quan hệ giữa yếu tố dự đoán và
các biến phản ứng hay không. Thống kê F càng xa 1 thì càng tốt.
+ coef - giá trị mô hình của chúng tôi, được tính toán thủ công trước đây.](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-114-320.jpg)


















![134
+ tier_2 = -0.675443;
+ tier_3 = -1.340204;
+ tier_4 = -1.551464;
+ const = -3.989979.
Using ID 1, Tier=3 as an example:
Sự khác biệt là do làm tròn số.
Lặp lại cho ID 3, trong đó tier = 1.
Một lần nữa, sự khác biệt là do làm tròn, điều này không đáng quan tâm.
Tuy nhiên, như đã đề cập trước đây, chúng ta muốn xác suất chứ không phải điểm
số. Vì vậy có thể tự tính toán hoặc nhờ Python thực hiện.
Chương trình 10-4: Sản xuất mô hình logistic xác suất.
Chương trình 10-4 chuyển tỷ số thành xác suất
Nếu chọn lấy các xác suất ngay lập tức, thì chúng ta có thể sử dụng Chương
trình 10-5:
Sản xuất mô hình logistic xác suất- phiên bản2
+ logistic1['pred_y1']=
điều này cho Python biết rằng chúng ta muốn tạo một biến mới trong
khung dữ liệu đã ghi được gọi là pred_y1.](https://image.slidesharecdn.com/phantichdulieuthongkevapython-211225221906/85/Phan-tich-du_lieu_thong_ke_va_python-134-320.jpg)












