Документ представляет собой пособие для учителей, содержащее задания для внеклассной работы по математике для учащихся 9-11 классов. Основное внимание уделяется развитию навыков решения нестандартных задач с использованием вычислительной техники и микрокалькуляторов, что обеспечивает более глубокое понимание математических методов и принципов. В пособии излагаются различные методы решения, позволяющие организовать как индивидуальную, так и коллективную работу учащихся.













![1) Найти дробные корни уравнения lgx + sinx=A 1.
Выпускник средней школы знает, что на (0;1)
функция y = gx и y = smx возрастающие. Но он, как
правило, не видит, какое это отношение имеет к реше
нию уравнения.
2) Решить уравнение cos(cosVl — *) Н—~ =
Л
= 1 + cosl.
На основании теоремы о производной сложной
функции ясно, что функция у = cos (cos,a/1 — х) убы
вающая (функция у — —х убывающая, y = AJx воз
растающая, у = cos* убывающая). Отсюда понятно, что
функция F(x) = cos(cos,a/ — х)-------------->определенная на
пи
(0; 1 ], убывающая. Поэтому данное уравнение имеет не
более одного корня. Так как Т7(1) = 1 _+_ cos 1, то для
решения уравнения не требуется вообще никаких
вычислений. Но в школьных учебниках и конкурсных
сборниках задач по математике ученик не видит такого
применения важнейших общих свойств функций. Поэто
му он считает это уравнение очень сложным.
3) Решить уравнение д/777* — 2250 + /77*3+ 108 =
= 6.
Школьник, не приученный смотреть на уравнение
с функциональной точки зрения, эту задачу не решает,
даже если он отлично знает все названные выше
свойства производной. Естественный подход к этой за
даче выглядит следующим образом:
Ле вая часть уравнения определена на 1-2^^ +50) • . ч
На этом промежутке непрерывные неотрицательные
функции у = 111 х — 2250 и у — Их3 + 108 возрастаю
щие. Функции у = л[х и у = л[х возрастающие. Поэтому
и сложные функции Р(х) = ~[111х— 2250 и К(х) =
= AJllx3+ 108 возрастающие. Функция F(x) = Р[х) +
+ К[х) непрерывная и возрастающая. Поэтому данное
уравнение имеет не более одного корня *0. При помощи
МК легко находим, что х0 = 3.
13](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-14-320.jpg)










![местами, то получим 36 и 72. При такой замене первый
множитель увеличился более чем на 10 %, а второй —
уменьшился менее чем на 4 %. Итак, получаем еще
одно приближение к ответу 91 • 36 • 54 • 72 • 80.
После замены множителя 36 на 63 получаем
91 -63 -54 -72 - 80.
Замечаем, что если поменять местами цифры 1 и 0,
то вместо множителей 91 и 80 получаем 90 и 81. Но
9 0 * 8 1 > 9 1 *80. Поэтому получаем еще одно прибли
жение к ответу: 90 • 63 • 54 • 72 • 81.
Замечаем, что сумма цифр каждого из множителей
в последнем произведении равна 9. Наверное, это
произведение и будет ответом на вопрос задачи. В са-
момделе, 90 • 63 • 54 • 72 • 81 = 95(6 • 7 • 8 • 9 -10).Ни
один из полученных в скобках сомножителей нельзя
больше увеличить, так как все они- должны быть
различными.
О т в е т . 90 • 63 • 54 • 72 • 81 = 1785641760.
З а д а ч а 8. Найдите целую часть числа
Ып + У я + 1 + Уга + 2 )2,
если п — натуральное число.
Р е ш е н и е . Обозначим
(Уга + У га + 1 + Уга 4~ 2 )2 = /(«), (1)-
[(Уга+У« +1 + Уга +2 )2]=ф (п).
Для получения гипотезы выполним математическое
моделирование, т. е. составим таблицу некоторых зна
чений функций f(n) и ф(п):
п f ( n ) <р(я) п f ( n ) ф ( п )
1 17,191508 17 11 107,87477 107
2 26,484036 26 12 116,88442 116
3 35,618441 35 13 125,89270 125
4 44,696680 44 14 134,89999 134
5 53,748090 53 15 143,90615 143
6 62,784516 62 16 152,91167 152
7 71,811721 71 17 161,91659 161
8 80,832771 80 18 170,92097 170
9 89,849589 89 19 179,92493 179
10 98,863327 98 20 188,92851 188
24](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-25-320.jpg)
![Таблица подсказывает, что
[(д/я + д/я + 1 + д/я + 2 )2] = 9я -f 8. (2)
Таблица приводит также к предположению, что
9я -f- 8 <с(д/я -f д/я"Ь 1 Н- д/я 4" 2) <С (9я —f~ 8) —(— 1. (3)
Для обоснования полученных гипотез преобразуем
функцию /(я) следующим образом:
/(я) = (д/я + д/я—+ 1 + д/я + 2 )2 = я + (я -f- 1) + (я -f-
—2) —|—2д/я • д/я -f- Т -f- 2 д/я • д/я -f- 2 -f- 2 д/я -)- 1X
X д/я +2 = 3/t —|— 3 —|— 2(д/я • д/я + 1 -f- д/я • д/я -f- 2 -f-
+ д/я + 1 • д/я + 2 ).
На основании теоремы о средних величинах
0,5(а + й)>д/а& (а, Ь > 0) получаем:
2д/я • д/я+ 1 < 2я + 1,
2дГп • д/я + 2 < 2я + 2,
2д/я+ 1 • д/я + 2 < 2я + 3.
Таким образом, /(я) С 9я + 9.
Теперь докажем неравенство
(УЛ + У«+ 1 +У« + 2)2>9« + 8. (4)
Исследуем при помощи производной функцию
/(*) = (д/х + л]х + 1 + -yjx+ 2)2 — 9* — 8
для х а 1. Находим:
/'(х) = 2д/х -J- д[х+ 1 + д1х+ 2 )/—!_ -f- ^ -
' 2д/л: 2дх+1
+ТАг)-9=-6+(л/А+л/А) +
+(лШ+лЯг)+(лШ+лШ>
Так как каждое значение выражения в круглой скоб
ке не меньше 2, то /'(*)> 0. Отсюда ясно, что /(я) —
25](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-26-320.jpg)
![возрастающая функция, и для доказательства неравен
ства (4) достаточно проверить его справедливость
при п = 1.
Таким образом, доказано, что
(Ы" + +1 + л/п + 2)2) =9п +8.
З а д а ч а 9. Найдите целую часть выражения
если число 1981 входит в него п раз (п а 2).
Р е ш е н и е . При помощи микрокалькулятора полу
чаем:
а, = -л/1981 да 44,508426;
52 = д/1981 + д/1981 да 45,005648;
а3 = д/1981 + д/1981 + л/1981 да 45,01 1 1 73;
а4 =4/1981 + д/1981 + д/1981 + -у/1981 да
да 45,01 1234;
а5 да 45,01 1234.
Отсюда появляется предположение, что целая часть
числа а равна 45, т. е. [а] =45.
Проверим это предположение следующим образом:
Допустим, что
у 1981 + д/1981 +-+У1981 + д/1981 >46.
Тогда д/1981 + ... + д/1981 + д/1981 > 135 и
1981 + ... + д/1981 + д/1981 > 1 352.
Продолжая этот процесс, приходим к очевидному
неверному неравенству. Поэтому [а] =45.
З а д а ч а 10.
Найдите все натуральные числа п такие, что сумма
S(n) цифр десятичной записи числа 2п равна 5.
Р е ш е н и е . Для поиска решения составим таблицу
значений выражения 2/г:
26](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-27-320.jpg)











![**7******* 112547Г
****** ]Д8781
_ 110177*
10037**
9799**
8783**
_ 10163**
10037**
_12 547*
12 547*
0
Из первых трех строчек ясно, что в 3-й строчке
третья цифра слева 6 или 7. Непосредственной провер
кой убеждаемся, что это будет только в том случае, если
Д = 3 или Д = 5 соответственно.
Легко проверить, что Д Ф 3. Итак, Д = 5. Теперь
очевидно, что Г = 3.
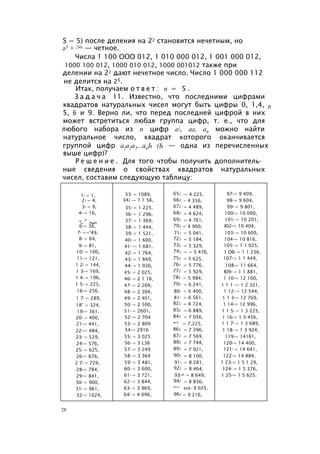
Окончательно находим: при делении числа
7375428413 на 125473 получаем 58781.
Задание 3. РЕШЕНИЕ УРАВНЕНИЙ
И НЕРАВЕНСТВ В ЦЕЛЫХ ЧИСЛАХ
З а д а ч а 1. При каких натуральных п (п л 2)
верно равенство
У 17д/5 + 38 + V 17д/5 - 38 = У~20? (1)
Р е ш е н и е . При помощи микрокалькулятора на
ходим:
17д/5 + 38 да 38,013154 + 38 да 76,013154 > 1;
17д/5 — 38 да 0,013154 < 1; д/20л 4,4721359.
Отсюда ясно, что положительная функция f(n) =
= д717д/5 + 38 является убывающей, и
а функция (р(п) =д/17 д/б — 38 — возрастающая, и
,ф(я) < 1. Для обнаружения некоторых свойств функции
я|?(ат) = f(n) + ф(я) выполним математический экспери
мент (составим таблицу значений функции ty(n) :
39](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-40-320.jpg)







![Логарифмируем обе части уравнения (2):
lg 9,242639 »lg 10,071065, отсюда
^ 1,038598.
Итак, — 1,038598. Но как найти т и я?
п
Очевидно, что т и п — это не однозначные нату
ральные числа, потому что даже 9:8 >> 1,038598 ... .
Продолжаем поиск при помощи микрокалькулятора:
10:9 > 1,038598 ... , 11:10 > 1,038598 ... , 12:11 >
> 1,038598 ..., , 26:25 > 1,038598 ..., 27:26 «
« 1,0384615 ..., 28*27 < 1,038598 ... .
Итак, появилась гипотеза, что m ="27 и п = 26. Но
как ее обосновать или опровергнуть?
Необходимо проверить справедливость равенства
(5 + 3 ~ [ 2 ) 2 7 = (3 + 5 д/2)26 или
5 + З д / 2 26------- 1 - И Л И
( 3 + 5 д/2~ ' 5-f 3 л ] 2
/ (5 + 3 л/2) (5Л2 — 3) 26._ 15-3л/2~) ИЛИ
' (5лЛ+3)(5л/2-3) ' (5 + 3 V2) (5 — 3д/2)
л 16Я22-+ 15 Л2665 -5 3-V3 у2
Но равенство (3) не может быть точным, потому
что в левой его части коэффициент при л [ 2 положитель
ный, а в правой части — отрицательный.
Теперь понятно, как доказать, что только пара (0; 0)
является целочисленным решением уравнения (1). Пре
образуем уравнение (1) следующим образом:
/ 5 -f* 3 ~ [ 2 п 1
Л3 + 5 V2~A (5 + 3'
Л 116у2/2 +151 5 у _ / 5 — 3 ~а/2~ т — п
)
Коэффициент -д/2 в левой части последнего равенст
ва положительный, а в правой части — отрицательный.](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-48-320.jpg)



![Проверяем эту гипотезу:
(1 + X + JT + ... + х п ~ ] ) ( + х + х2 + ... + х п + *) =
= ((1 + X + Х " + ... -f- хп) — х п ) • ((1 4" X + X " 4" ... -f-
+ х п ) - - х п + ' ) = { + х + х 2 + . . . + х п ) 2 + х п + 1 { + * +
+ *2 + ... + х п ) - х п { + х + х 2 + ... + х п ) - =
= ( + х + х 2 + ... + x n f + x n + ' + х п + 2 + ... +
+ X 2 n + 1 - х п - х п + 1 - х п + 2 - ... — x 2 n — x 2 n + 1 =(1 +
+ х + х2 + х3 + ... + х п ) 2 - х п .
Задание 5. ЗАДАЧИ ПО ПЛАНИМЕТРИИ
З а д а ч а 1. В треугольнике A B C величины углов
В и С равны по 40°. Докажите, что если отрезок B D —
биссектриса угла В , то B D + D A = В С .
П е р в о е р е ш е н и е . Угол В D C равен 120° (рис. 1).
Поэтому B C > B D и на стороне В С можно отложить
отрезок B E , равный B D . Теперь докажем, что Е С — A D .
Имеем А В Л Е = A B E D = 8 0 ° . Поэтому / L E D C =
= 2 0 ° — 80° = 40° = Z . D C E и Е С = E D . Кроме того,
г L A D E = 1 4 0 ° , и так как А А В Е = 4 0 ° , то Z . A D E +
+ Z. А В Е = 180°. Поэтому четырехугольник A B E D
вписывается в окружность. Отсюда следует, что
A A E D = 2 0 ° и Z . D A E = 20°. Таким образом, A D =
= D E — Е С и Е С = A D . Итак, В С = B E + Е С = B D +
+ D A .
В т о р о е р е ш е н и е . Рассмотрим треугольник
В С М , для которого D — точка пересечения биссектрис
(рис. 2). Строим D E A - B M и D F - L C M . Замечаем, что
Z. D G F = Z. D A E = 80° и D E — D F . Отсюда следует,
что треугольники D A E и D G F равны. Поэтому
D G = D A . Отсюда B D -f D A = B D + D G = B G = В С ,
так как A B C G = Z - B G C .
Т р е т ь е р е ш е н и е . Через точку D проводим
прямую, параллельную прямой В С (рис. 3). На стороне
В С откладываем отрезок B N t равный отрезку B D .](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-52-320.jpg)





![сы внутренних углов лежат на высотах треугольни
ка A B C .
Р е ш е н и е . Пусть точка М есть пересечение высот
А А , В В 1 и СС1 остроугольного треугольника A B C .
Углы А С М и А В М прямые. Поэтому точки С и В
принадлежат окружности, диаметром которой является
отрезок A M . Углы С А М и С В В равны, потому что
они вписаны в одну и ту же окружность и опираются
на хорду М С ] .
Углы С В М и С А М прямые. Поэтому точки В и A
лежат на окружности с диаметром М С . Значит, углы
В В А и В С С 1 равны.
Из треугольников А В А и С В С следует, что
Z . B A A { = / - В С С = 90° — Z . A B C .
Таким образом, углы В В С и В В А равны. Отсюда
ясно, что луч В В есть биссектриса угла С В А .
Аналогично доказывается, что лучи А А и С С яв
ляются биссектрисами углов С А В и В С А .
З а д а ч а 6. Пятиугольник A B C D E вписан в окруж
ность. Расстояния от вершины А до прямых В С , CD,
D E равны соответственно а , b , с.
Найдите расстояние /г от точки А до прямой B E .
Р е ш е н и е . Построим произвольную окружность и
впишем в нее какой-нибудь пятиугольник A B C D E
(рис. 5). Из вершины А опустим перпендикуляры
А Н , А К , A M , А Р соответственно на прямые В С ,
B E , CD, D E .
Измерив масштабной линейкой отрезки А Н , Л/(, уШ,
А Р , получаем гипотезу, что h : a = c : b .
Построим еще какой-нибудь пятиугольник, вписан
ный в окружность, и, выполнив соответствующие
измерения, снова получаем, что h a & c b .
Рис. 5
56](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-58-320.jpg)

















![Рис. 1
* В
1:
-/
}1 ~ о
11
с Я 7
1
1/
L
Рис. 2
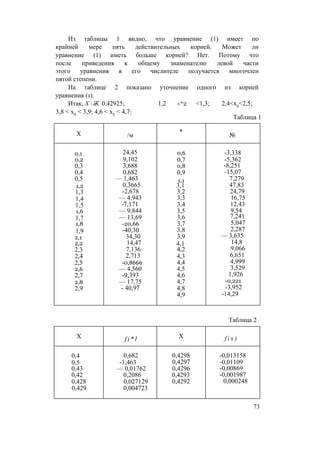
Выражения х и |3 — 2х| обращаются в нуль со
ответственно в точках 0 и 1,5. Графиком функции f ( x )
является ломаная. Для ее построения вычисляем:
/(0) = —2; /(1,5) = 4; /(-1)= -4; /(2) = 4 (точка -1
лежит левее точки 0, а точка 2 расположена правее
точки 1,5)/
Прямая D E , очевидно, параллельна оси абсцисс.
Поэтому график функции /(х), т. е. ломаная A B D E
пересекает ось абсцисс только в одной точке С . Из
подобия прямоугольных треугольников О С В и F C D
следует О С = 0,5. Получаем о т в е т : (0,5; + оо).
З а д а ч а 4. Решите неравенство
7
U— 1| —3
> U + 2I. (1)
Р е ш е н и е . Строим графики функций /(*)= U +
+ 2 | | , ср(х) = х — 11 — 3, f>(x) = 7:ф(х)(рис. 3). Графики
этих функций легко строятся без применения произ
водной, так как они монотонные на соответствующих
промежутках.
Прямые х = — 2 и х = 4 являются вертикальными
асимптотами графика функции г|)(х).
Для определения абсцисс точек В и С решаем со
ответственно уравнения
Получаем £(5; 7) и C ( — ~[l — 2 f A J l ) . С помощью
рисунка 3 получаем о т в е т : [ — V 7 — 2; —2), (4; 5].
З а д а ч а 5. Решите неравенство х — 2 А д [ х .
75](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-77-320.jpg)
![Р е ш е н и е . Строим графики функций /(х) = х — 2
и ц ( х ) = л / х (рис. 4). После этого становится понятным,
что уравнение х — 2 = л [ х имеет только один положи
тельный корень Х о > 2, а решением данного неравенства
является промежуток [0; хо], так как данное неравенство
определено только для неотрицательных чисел.
Решив уравнение х — 2 = л [ х путем возведения его
обеих положительных частей в квадрат, получаем
х0 = 4.
Здесь надо заметить следующее:
Во-первых, уравнение (х— 2)2 = х не равносильно
уравнению х — 2=А~[х. Первое из них имеет корни
1 и 4, а второе — только 4. Из рисунка ясно, почему
число 1 является посторонним корнем для уравнения
х — 2 =л[х (точка А есть пересечение графиков функ
ц и й / ( х ) = х — 2 И ф|(х) =---------- [х).
Во-вторых, предварительно построенные графики
функций /(х) и ф(х) снимают вопрос о посторонних
корнях соответствующих уравнений и неравенств.
З а д а ч а 6. Назовите множество решений нера
венства
"Л7 + х а> 5 — х. (1)
Р е ш е н и е . Строим графикинепрерывных монотон
ных функций:
f ( x ) = а 7 + х и ф(х) — 5 — х.
Функция /(х) определена на промежутке [ — 7; + оо),
непрерывна и монотонно возрастает. Она изменяется
от 0 до + оо. Функция ф(х) определена для всех дейст
вительных чисел, она монотонно убывает от + оо до
76](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-78-320.jpg)
![— оо. Поэтому уравнение l - - x = 5 — х имеет един
ственное решение лго- Легко заметить, что Х о = 2. С по
мощью графика находим о т в е т : (2; + оо).
З а д а ч а 7. Решите неравенство ~ y j x — 1 +
-f- ~ J х + 14 л 3.
Р е ш е н и е . Левая часть неравенства определена
на промежутке [1; +оо). Функция f i ( x ) = J J x — 1 не
прерывная и монотонная (на указанном промежутке
возрастает от 0 до -f-oo). Функция /г(*) = л / х 14
непрерывная и монотонная (на промежутке [1; + оо)
возрастает от ~f5’ j x o + оо), поэтому непрерывная
функцияf ( x ) = f ] ( x ) + f - 2( x ) на полуинтервале [1; + оо)
возрастает от "Л15 до + оо*. Так как тосу-
ществует единственная точка х 0 такая, что f ( x о) — 3.
Очевидно,Х о — 2 . О т в е т , х л 2 .
З а д а ч а 8. Решите неравенство
^ .Vf-.+ l < 1. (1)
1 — 2 “/3 — х
Р е ш е н и е . Выражение 2 ~ у х определено на
полуинтервале [ — 1; +оо). Выражение 1 — 2 ~ / з — х
определено и отлично от нуля на промежутках (— о о ;
2,75) и (2,75; 3], поэтому неравенство (1) определено
на промежутках [ — 1 ; 2,75) и (2,75; 3].
Строим графики функций: f ( x ) = 2л]х + 1 и ф(х) =
= 1 — 2л] 3 — х на промежутках ( — 1 ; 2,75) и (2,75; 3].
Так как на полуинтервале [ — 1 ; 2,75) функцияf ( x )
неотрицательна, то л О на этом промежутке и
полуинтервал [— 1; 2,75) является решением неравен
ства ( 1 ).
Функцииf ( x ) и ф(х) на полуинтервале (2,75; 3] поло
жительные и возрастающие: "У 15 С f ( x ) л 4; 0 <
< ф(х) л 1. Поэтому на промежутке (2,75; 3] f ( х >
> 1 > 1
О т в е т . [ — 1; 2,75).
З а д а ч а 9. Решите уравнение
log3*=i+^r- 0)
13](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-79-320.jpg)
![Р е ш е н и е . Строим графики
функций f ( x ) = log3*, <р(х) =
= 1 + 2 Г А Т (Рис- 5)-
На полуинтервале (— оо; 0]
функция f ( x ) не определена,
поэтому на этом промежутке
нет решений уравнения (1).
На интервале (0; 0,5) функ
ция ф(х) положительна, а фун
кция f ( x ) отрицательна, поэтому
и здесь нет решений уравне
ния ( 1 ) .
В точке лг = 0,5 функция ф(х) не определена.
На полуинтервале (0,5; 1] функция /(*)> — 2, а
функция ф(лг)< —2.
На интервале (1; 2) функция f i x ) положительна,
а функция ф(х) отрицательна.
В точке х = 2 функция ф(л:) = 0, а функция f ( x )
положительна.
На полуинтервале (2; 3] функция .ф(лг) < 0,4, а функ
ция f ( x ) > 0,4.
Наконец, на промежутке (3; + оо) функция ф(х) < 1,
а функция f ( x ) > > 1.
Таким образом, уравнение (1) не имеет решений.
Задание 8. ИРРАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
И НЕРАВЕНСТВА
З а д а ч а 1. Решите уравнение ~2х + 5 = 8 —
— у * — г
П е р в о е р е ш е н и е . Преобразуем уравнение к
виду:
•д/2* + 5+ л]х — 1 = 8.
Функция f ( x ) = -j2x + 5 +Ул; — 1 определена для
х л , непрерывная и возрастающая. Очевидно,
f ( ) = - v <,8. Поэтому существует единственный ко
рень Х .
Находим значение функции f { x ) при некоторых
значениях х: /(2) = 4, /(5) » 6, /(17) = -[9 + 4 > 8.
После чего ясно, что 5 < * i < 17. Нетрудно заметить,
что /(10) = 8.
78](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-80-320.jpg)
![В т о р о е р е ш е н и е . Возводим обе части уравне
ния в квадрат. Получаем:
2* + 5 = (8 — У* — I)2 или
1 бУ* — 1 = 58 — х.
Возводим в квадрат обе части последнего уравнения
После приведения подобных членов получаем:
х2 - 372* + 3620 = 0.
Корни этого уравнения: х = 10, *2 = 362.
Каждое новое уравнение было следствием преды
дущего. Поэтому в процессе решения уравнения (1)
могли появиться посторонние корни. Следовательно,
полученные корни нуждаются в проверке:
/(Ю) = 8, /(362) = 46.
Отсюда ясно, что уравнение (1) имеет единствен
ный корень * = 10.
З а д а ч а 2. Решите уравнение____________
~] Зх —1 = 3 —{- л] х — 1. (1)
П е р в о е р е ш е н и е . После возведения обеих ча
стей уравнения (1) в квадрат получаем:
3* 1 = 9 6 У* — -J- (* — 1)
или
6 -у/х — 1 = 2 х - 7 . (2)
Уравнение (2) после возведения его обеих частей в
квадрат преобразуется к виду: 4*2 — 64* + 85 = 0.
Его корни: *i = 0,5(16 + зУГЁГ) ~ 14,539; *2 = 0,5(16 —
— зУнГ)« 1,4615.
Проверка (при помощи микрокалькулятора) пока
зывает, что только число *i является его решением.
В т о р о е р е ш е н и е. Найдем наибольшее значение
функции /(*) = 3 +У* — 1 — Уз* + 1 при помощи
производной:
1 2
/'(*)=
5
Решив уравнение /'(*) = 0, получим *— у. Очевидно,
^ f I — 1 и /(1)= 1, НО У > *2. Поэтому только число
*1 является решением уравнения ( 1 ).
79](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-81-320.jpg)

![Строим графики функ- у
цийf ( x ) и ф(х) (рис. 1).
Что дает внимательное
изучение таблиц и графи
ков функций /(х) и ф(х)?
Во-первых, становится
ясным, что решением дан
ного уравнения является _
число 1.
Во-вторых, на отрезке
[1,5; 9] функция /(х) непо
ложительная, а функция
ф(х) положительная. Поэтому на этом промежутке
решений уравнение (1) не имеет.
В-третьих, на интервале (9; + оо) функции /(х) и
ф(х) положительны.
Графики этих функций подсказывают, что на интер
вале (9; + оо) целесообразно заменить выражение
- У х '— 9 на д/х — 3. Очевидно, л / х — 3 >> д/х — 9 на
(9; +оо). Правую же часть уравнения (1) уменьшим,
вычтя из него 6.
Итак, попытаемся доказать, что на интервале (9;
+ оо) верно неравенство
.-у/х — 3 < ( х — З)3. (2)
После возведения обеих частей неравенства (2) в куб
получаем:
(х-3)[(х-3)8- 1]>0. (3)
На промежутке (9; + оо) неравенство (3) верно. Значит,
на этом промежутке верно неравенство (1) и, следова
тельно, неравенство ф(х) ;>/(х).
Таким образом, показано, что на промежутке
[1,5; + оо) уравнение (1) решений не имеет.
На промежутке (1; 3] функция /(х) вогнутая, а функ
ция ф(х) — выпуклая. Поэтому на этом промежутке
график функции f ( x ) лежит под хордой А С , а график
функции ф(х) лежит над хордой А В (рис. 1). Отсюда
ясно, что и на полуинтервале (1; 3] уравнение (1) реше
ний не имеет.
На интервале (—оо; 1) график функции f ( x ) нахо
дится над прямой А В , а график функции ф(х) лежит
под прямой А В . Поэтому и на промежутке (—оо; 1)
уравнение (1) решений не имеет.
81](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-83-320.jpg)
![Таким образом, только число 1 является действи
тельным корнем уравнения ( 1 ).
З а д а ч а 4. Решите неравенство
~{jx2 + 2х + 10 + х4 Л 62 — 32х. (1)
Р е ш е н и е . Так как г2 + 2х + 10 = (х + 1 )2 + 9 > 0
при любом значении л:, то данное неравенство опре
делено при любом действительном значении х. Иссле
дуем некоторые свойства непрерывной функции
f (х) = ~J{x -f- 1 )2 -f- 9 -j- х4 -j- 32х— 62. (2)
Если х Л О , то непрерывная функция f ( x ) — возра
стающая. Поэтому уравнение f ( x ) = 0 имеет не больше
одного неотрицательного корня х . Но /(0) < 0 и
/(2) > 0, поэтому 0 < х < 2.
Неравенство д/(х + I)2 + 9 > 0 верно при любом
значении х . Поэтому уравнение f ( x ) = 0 не имеет корней
для тех значений х , которые являются решениями не
равенства х 4 + 3 2 х — 62 л 0.
Получаем х 4 + 3 2 х — 62 = х(х3 + 32) — 62. Если
х < — 4, то х3 + 32 < — 32 и х(х3 + 3 2 ) > 128. Поэтому
при х < — 4 верно неравенство х + 3 2 х — 62 > 0.
Теперь ясно, что отрицательные корни уравнения
/(jc) = 0 могут принадлежать только интервалу ( — 4; 0).
При помощи программируемого микрокалькулятора
составляем таблицу значений функции f ( x ) :
X — 4 -3,5 -3 — 2/5 -2 — 1,5 -1 -0,5 0
f i x ) 68 -22 -75 — 101 -108 -103 -91 -76 -60
На основании этой таблицы можно предположить,
что на отрезке [ — 3,5; 0] уравнение f ( x ) = 0 не имеет
корней. Но как это доказать?
Очевидно,
д/э <7(х+ 1)2 + 9<л/(-3,5+ 1)2 + 9.
Отсюда
1,73<-ЭД* + 1)2 + 9< 1,98. (3)
Выясним, как изменяется функция ф(х) = х4 +
+ 32х —62 на отрезке [ — 3,5; 0]. Находим ф'(х) =
82](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-84-320.jpg)
![= 4х3 + 32. Решив уравнение 4г3 + 32 = 0, получаем
х = — 2. Вычисляем:
ф(— 2) = - 110; Ф(0)= -62; ф(-3,5)« -23,9375. (4)
Из условий (3) и (4) ясно, что на всем отрезке
[ — 3,5; 0] функция /(лс)<0.
На отрезке [ — 4; —3,5] непрерывные функции
у = ~](х + 1)2+ 9 и ф(дс) убывающие. И так как
/(— 4) « 68 > 0, а /(— 3,5)« — 22 < 0, то на интервале
( — 4; —3,5) существует единственный корень Х 2 урав
нения f ( x ) = 0.
Для уточнения значений корней х и Х 2 составим
при помощи микрокалькулятора таблицу значений
функции f ( x ) :
л; № X /М
0 -60,22 — 4 68,06
2 20,06 -3 -75,1
1,5 -7,00 -3,5 -21,96
1,6 -2,25 -3,7 9,02
1,7 2,76 -3,65 0,6897
1,65 0,9754 -3,64 -0,92905
1,64 — 0,287 — 3,645 — 0,12166
1,643 — 0,13743 -3,646 0,04029
1,644 — 0,087508
1,645 — 0,037553
1,646 0,012434
Итак, х ж — 3,6455; Х2~ 1,6455.
Легко заметить, что х + Х « — 2, Х Х 2 ~ — 6.
Решив систему уравнений: х--Х2= ------------------- 2, *1X2=— 6,
получим гипотезу:
*1 = — -/7 — 1, х2 = -ф — 1.
Непосредственной подстановкой х и Х 2 в уравнении
f ( x ) = 0 убеждаемся в справедливости этой гипотезы.
З а д а ч а 5. Решите неравенство
2л2х + 8 + -Л303 - 5* > 7. (1)
Р е ш е н и е . Исследуем на экстремум и монотонность
непрерывную функцию
/(*)' = 2л2х + 8 + -Л303 - 5х. (2)
83](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-85-320.jpg)



![П е р в о е р е ш е н и е . Решаем неравенство (1) отно
сительно параметра:
х 2 — а х — х + а + 1 > О,
х 2 — х + 1 > а х — а,
а ( х — 1) С х2 — х + 1. (2)
Так как х < 1, т. е. - 1 1, то х - 1 <0 и из
неравенства (2) получаем (для х — 1 Ф 0!):
Строим график функции а ( х ) = х + ~ f на — 1
< JC < 1
Для этого вычисляем:
«'(*) = - -(Г=тг=0-
Корнем этого уравнения, принадлежащим полуинтер
валу [— 1; 1], является только 0. Вычисляем: а(0) = — 1;
а ( — 1) = — 1,5; а(1) = — оо.
С помощью графика получаем о т в е т :
— 1 < С а < С + о о .
В т о р о е р е ш е н и е . График функции а ( х ) можно
построить при помощи микрокалькулятора (и без по
мощи производной!). При помощи микрокалькулятора
легко обнаруживаем, что нужное нам наибольшее
значение функция а ( х ) достигает в точке х = 0. После
этого остается доказать, что
А это уже совсем простое дело.
З а д а ч а 4. Решите уравнение
х ~ { + а х = 1 (1)
и неравенства x ~ l + а х >1 (2)
x ~ l + а х < 1 (3)
относительно х ( а — параметр) и выполните исследова
ние свойств их решений.
Р е ш е н и е . Очевидно, х Ф 0. Решаем сначала урав
нение (1) и неравенства (2) и (3) относительно
параметра а :
х — 1
а =
(4)
87](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-89-320.jpg)
![Из неравенства (2) получаем:
cl > х - $ если х>>0; (5)
а С х-д_ если х < 0 . (6)
Из неравенства (3) получаем:
если (7)
а > если х < 0 . (8)
Исследуем функцию а =— т X
(1 - 1 ). Эта
функция является квадратичной относительно х ~ По
этому ясно, что она принимает наибольшее значение
в точке х_1=0,5, т. е. при х = 2 .
Обозначим X ] и х2 — корни уравнения ( 1 ), причем
Х < *2.
Построим график функции а = х ~ х —х ~ 2 . С по
мощью его можно ответить на следующие во
просы:
1. Почему график функции а = х ~ 1 —х ~ 2 пересе
кает ось абсцисс только в одной точке?
2. Почему график этой функции не пересекает ось
ординат?
3. При каких значениях параметра а уравнение (1)
не имеет решений?
О т в е т , а > 0,25.
4. При каких значениях параметра а уравнение (1)
имеет только одно решение?
О т в е т . При а = 0.
5. При каких значениях параметра а уравнение (1)
имеет наибольшее число корней?
О т в е т . 0 < а < 0,25; а < 0.
6. При каком значении а положительный корень
уравнения (1) будет наименьшим?
О т в е т , а — 0,25.
7. Как изменяются корни уравнения ( 1 ), если
а < 0 и неограниченно уменьшается?
О т в е т . Оба корня уравнения (1) стремятся к нулю.
8. Сравните х и х2, если а < 0.
Решив уравнение (1) относительно х у получаем:](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-90-320.jpg)



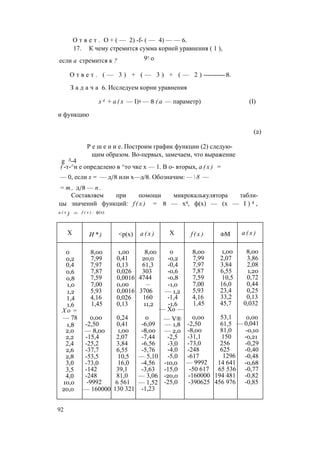
![С помощью таблицы строим графики этих функций
(рис. 2).
Выясним свойства функций f ( x ) , ф(х) и а ( х ) видны
из таблицы и графиков. Какие из обнаруженных свойств
мы сможем обосновать?
Функция f ( x ) принимает наибольшее значение в
точке 0, и /(0) = 8. Она изменяется от — оо до 8. Ее
график пересекает ось абсцисс в точках т и п и сим
метричен относительно оси ординат.
Функция <р(х) неотрицательна; ф( 1) = 0. Она изме
няется от 0 до + о о . Ее график симметричен относи
тельно прямой а = 1.
Функция а ( х ) есть частное функций f ( x ) и ф(х).
На промежутке [т; 0] функции f ( x ) и ф(х) положи
тельны; функция f ( x ) возрастает от 0 до 8, а функция
ф(х) убывает. Поэтому функция а ( х ) = - А щ на этом
промежутке возрастает от 0 до 8.
Таблица и графики функций указывают на то, что
отрицательная функция а ( х ) на (— о о ; т ) больше — 1 и
монотонно возрастает до 0.
Докажем, что если х < С т у то а ( х ) > —1.
Очевидно,
Поэтому если бу
дет доказано не
равенство
то тем самым
докажем, что
а ( х ) > — 1. Но
если х < — 1.
Поэтому верно и
неравенство
а ( х ) > — 1,
если х<С т <С — 1.
93](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-95-320.jpg)


![Таблица 1
X т фМ а ( х ) X я т ф(х) . Ф )
-1,0 5,0 — 1,0 5,0
-1,2 5,6 50 55,6 -0,8 4,4 -30,0 -25,6
— 1,4 6,4 15 21,4 -0,6 4,0 -15,0 -11,0
— 1,6 7,2 10 17,2 -0,4 3,6 — 10,0 -6,4
-1,8 8,0 7,5 15,5 -0,2 3,2 -7,5 -4,3
-2,0 9,0 6,0 15,0 0,0 3,0 -6,0 -3,0
-2,2 10,0 5,0 15,0 0,2 2,8 -5,0 -2,2
-2,4 11,2 4,3 15,5 0,4 2,7 -4,3 -1,6
-2,6 12,4 3,8 16,2 0,5 2,5 — 4,0 -1,5
-2,8 13,7 3,3 17,0 0,8 2,9 -3,3 -1,4
-3,0 15,0 3,0 18,0 1,0 3,0 -3,0 0,0
-3,2 16,4 2,8 19,2 1,2 3,2 -2,7 0,5
-3,4 18,0 2,5 20,5 1,4 3,6 -2,5 М
-3,6 19,6 2,3 21,9 1,6 ' 4,0 -2,3 1,7
-3,8 21,2 2,1 23,3 1,8 4,4 -2,1 2,3
— 4,0 23,0 2,0 25,0 2,0 5,0 -2,0 3,0
Строим графики функций /(*), ср(х) и а ( х ) (рис. 3).
В таблице 2 уточнено наименьшее значение функции
а ( х ) на отрезке [ — 3; —2]: а(хо) ~ 14,961944; х 0 ~
& -2,0785:
Таблица 2
а { х ) X а ( х )
— 2,0 15,0 — 2,06 14,96398
-2,2 15,04 -2,08 14,961955
-2,15 14,99 -2,075 14,96202
-2,05 14,967 -2,085 14,962179
-2,03 14,976 -2,081 14,961977
-2,07 14,9624 — 2,079 14,961945
Используя таблицы 1, 2 и рисунок 3, ответьте на
следующие вопросы:
1. Назовите наименьшее значение функции f ( x ) .
2. Чему равно наибольшее значение функции f ( x )
на отрезке [0; 2].
3. Назовите наименьшее значение функции f ( x ) на
полуинтервале ( — 1 ; 0].
4. Назовите наименьшее значение функции f ( x ) на
интервале (— 1; 1).
5. На каком промежутке функцияf ( x ) убывает?
96](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-98-320.jpg)
![6. На каком проме
жутке функция f ( x ) воз
растает?
7. Докажите, что фун
кция ф(х) на интервале
( — 4; —1) возрастает.
8. Назовите прибли
женное значение х, при
котором верно равенство
f { x ) == ф(х).
9. Почему уравнение
f ( x ) = ф(х) имеет только
одно решение?
10. Верно ли, что фун
кция ф(х) возрастающая?
11. Чему равно наи
большее значение функ
ции ф(х) на полуинтервале
(-1; 2]?
12. В скольких точках
график функции ф(х) пе
ресекает ось ординат?
13. Почему график
функции ф(х) не пересека
ет оси абсцисс?
14. Докажите неравенство а ( х 14, если — 2 , 2 А
< л < — 2, 0.
Р е ш е н и е . Непрерывная функция f ( x ) на отрезке
[ — 2,2; —2,0] убывает от 10 до 9 (см. таблицу 1).
Непрерывная функция ф(х) на этом отрезке возрастает
от 5 до 6. Но а ( х ) = f ( x ) + ф(А). Поэтому на отрезке
[ — 2,2; —2,0] функция а ( х ) не может быть меньше
14(9 + 5=14).
15. Докажите, что уравнение /(х) = ф(х) не имеет
положительных корней.
16. Имеет ли корни уравнение а ( х ) = ф(х)?
Р е ш е н и е . Не имеет, потому что а ( х ) = ф(х) + f ( x )
и /(*) > 0.
17. Почему функция а ( х ) возрастает на промежутке
[0; 0,5]?
Р е ш е н и е . На этом промежутке f ( x ) убывает от
3 до 2,5, а функция ф(х) возрастает от —6 до —4.
Поэтому а ( х ) возрастает.
18. При каких значениях параметра а уравнение
х 3 + (2 — а ) х — а — 3 = 0 не имеет корней?
4 А. Б. Василевский 97](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-99-320.jpg)

![Как изменяются cos х , 2 s i n x + 5, ^"+5 и -
— 2,5,если х увеличивается от 0,5л до л? Докажите,
что на отрезке [0,5л; л] уравнение (3) имеет един
ственный корень.
З а д а ч а 4. Докажите, что уравнение
3 tg 2л: — 4 tg Зл: = tg2 З х tg 2 х (1)
Уе имеет корней, принадлежащих интервалу л0;
Р е ш е н и е . Если 0 < С х < у , то функции tg 2 х и
i g 3 x положительные и возрастающие. Отсюда ясно,
что на л0; левая часть уравнения (1) отрицатель
на, а правая положительна.
З а д а ч а 5. Уравнение
3 tg 2л: — 4tg3* = tg23xtg2x (1)
преобразовали следующим образом:
tg 2 х = —, (2)
' 3 — tg2 Злг w
tg 2х 3 З х _ Зл_ ■ (3)
Какие два из уравнений ( 1 ), (2), (3) равносильны
между собой?
З а д а ч а 6. Сколько решений имеет уравнение
arcsin 2 х + arcsin х — (1)
Р е ш е н и е . Функция f ( x ) = arcsin 2 х определена на
отрезке [ — 0,5; 0,5], а функция ф(х) = arcsin х опреде
лена на отрезке [ — 1; 1]. Поэтому левая часть уравне
ния (1) определена на отрезке [ — 0,5; 0,5].Монотон
ная и непрерывная функция у = arcsin 2 х + arcsin х
изменяется на отрезке [ — 0,5; 0,5] от л—5. —JL ) до
(я . я 2 2т т я _ 2т - г
Т ' Т )’ т' е‘ от J n до Т71' Т <TJt* Поэтому
уравнение (1) имеет единственное решение.
З а д а ч а 7. Уравнение
1 + cos 2х cos Зх = 0,5 sin2 Зх (1)
99](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-101-320.jpg)

![Рассмотрев таблицу, можно предположить, что на
отрезке [0; 2л] уравнение имеет только один корень
X i = а в остальных точках этого отрезка функция
f ( x ) положительная.
Наименьшее значение правой части уравнения (1)
равно "У2 Ав точках х = ~ и * ~ у Выясним, чему
равно наибольшее значение левой части этого данного
уравнения. Для этого исследуем функцию ф(х) =
= sin х + cos х. Находим ф'(х) = cos х — sin х. Оче
видно, ф'(х) = 0, если х — Вычисляем ф а у а = 2.
Итак, уравнение (1) на отрезке [0; 2л] имеет един
ственный корень х =
З а д а ч а 9. Уравнение
4 sin4 З х — 3 cos х + 5 = 0 (1)
преобразовали к виду:
COS X =1!-1_о—. (2)
В каких пределах изменяются функции /(х) = cos х
/ ч 4 sin4 З х 4- 5
И <р{*) =.............з ?
Сколько решений имеет уравнение ( 1 ) ?
О т в е т . Уравнение (1) не имеет действительных
корней.
З а д а ч а 10. Неравенство
л/2х + 5 а 8 — д/х — 1 (1)
преобразовали к виду:
д/2х + 5 + д/х 1 а 8. (2)
Докажите, что функция /(х) == д/2х + 5 +д/лс ~ 1
возрастающая. Почему уравнение д/2х + 5 + д/х — 1 ==
— 8 имеет единственный корень х = 10? Назовите все
решения неравенства (2).
О т в е т. х а 10.
З а д а ч а 11. Докажите, что уравнение д/х + 3-f-
— 2 = 7 имеет единственный корень Х.
101](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-103-320.jpg)
![Р е ш е н и е . Функцияf ( x ) = л / х + 3 -f л/Зл: — 2
Л . 2
определена для лг л —, возрастающая, непрерывная,
/(■|-) = < 7. Легко заметить, что лч = 6.
З а д а ч а 12. Уравнение
-/22 —л; —/10 —* = 2 (1)
преобразовали следующим образом:
(-V22 — х — -/10 — х ) (~/22 — х + ~/10 — л:) 2-
~у/22 — л: + “д/lO — х
* (22 — х ) — (10 - х ) _д.
л22 - л: + -т/Ю - л:
-V ^------------- .---------- = 1- (2)
”у22 — л; + "у 10 — х
Для каких значений х определена функция f ( x ) =
= “/ 22 — лс + ЛЮ — х ?
Докажите, что функции f ( x ) и ф(лг)== монотонные.
В каких пределах изменяются функции f ( x ) и ф(л:)?
Сколько решений имеют уравнения (2) и (1)? Назо
вите целое число, которое является решением уравне
ний (2) и (1).
З а д а ч а 13. Найдите наименьшее значение функ
ции
t|)(jc) = -/15 — 12 cosx + "л7 — 4д/з sin х (1)
на отрезке [0; 0,5я].
Р е ш е н и е . Т а к к а к | c o s x | л 1 и | s i n x | < 1 , то
функция я|)(лг) определена на всем отрезке [0; 0,5л1.
Для поиска свойств функций f ( x ) = A J 15 — 12 cos х ,
ф(х)= у7 — sin лг, ^ф(х) = f ( x ) -j- ф(лг) составляем
при помощи микрокалькулятора таблицу их значений:
102](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-104-320.jpg)
![* о
/<*) <рМ <р(х)
0 1,7320508 2,6457513 4,3778021
5 1,7451827 2,5290645 4,2742472
10 1,7839021 2,4076816 4,1915837
15 1,8463179 2,2818523 4,1281702
20 1,9296859 2,1518401 4,0815260
25 2,0308387 2,0179237 4,0487624
30 2,1465542 1,8803984 4,0269526
35 2,2738018 1,7395827 4,0133843
40 2,4098684 1,5958185 4,0056869
45 2,5523945 1,4494896 4,0018841
50 2,6993608 1,3010333 4,0003941
55 2,8490493 1,1509769 4,0000262
60 3,0000020 0,9999989 4,0000001
65 3,1509650 0,84906731 4,0000323
70 3,3008723 0,69972737 4,Q003597
75 3,4487928 0,55485998 4,0036527
80 3,5939145 0,42077535 4,0146899
85 3,7355228 0,31330512 4,0488279
90 3,8729833 0,26794924 4,1409325
На основании таблицы можно высказать предполо
жение, что на отрезке [0; 0,5я] функция i|?(x)>4, при
чем ) — 4-
Итак, попытаемся доказать, что
-л/15 — 12 cos х+ "А7 — 4А3 sin 4. (2)
Пусть д/7 — 4-/з sin x = t .
7 /2 I ( 7 /22
Отсюда sinx = —, cosx = - / l------------------------------ а— и нера-
4 д/3 v
венство (2) принимает вид:
V l 5 - V 3 - V 4 8 - ( 7 - / 2 ) 2 > 4 - A . (3)
Обе части неравенства (3) неотрицательны, поэтому
после возведения его обеих частей в квадрат получаем
равносильное неравенство
15 — д/3 • л/48 — (7 — /2)2 >(4 - О2
ИЛИ
-/3'У48-(7-/2)2<8А- 1 -/2.
Отсюда /4 — 4/3 + 6/2 — 4/ + 1 а 0.
103](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-105-320.jpg)

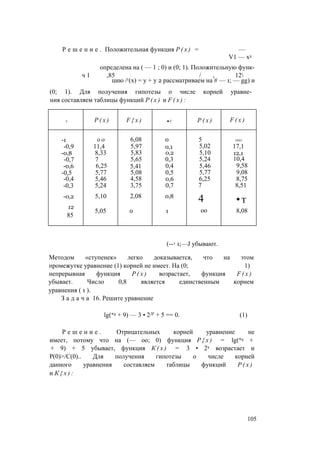
![X Р ( х ) К ( х ) X Р ( х ) К { х )
0 5,954 3 1,6 6,062 9,09
0,2 5,956 3,45 1,8 6,087 10,4
0,4 5,961 3,95 2 6,113 12
0,6 5,971 4,55 2,2 6,141 13,8
0,8 5,984 5,22 2,4 6,169 15,8
1 6 6 2,6 6,197 18,2
1,2 6,018 6,89 2,8 6,226 20,9
1,4 6,039 7,92 3 5,255 24
Теперь можно сделать предположение, что если
х > 2 , то lg(x2 + 9)<2* (это неравенство легко дока
зывается при помощи производной). После этого ста
новится ясным, что все корни данного уравнения при
надлежат отрезку [0; 2]. Число 1 является корнем
уравнения.
Из таблицы ясно, что отрезкам [0; 0,8] и [1,2; 2] не
могут принадлежать корни уравнения (1).
Для доказательства того, что 1 является единствен
ным корнем уравнения (1), составляем таблицы функ
ций Р ’ ( х ) и к ’ ( х ) :
Р ’ ( х ) К ’ ( х ) Р ’ ( х ) К ’ ( х )
0,8 0,072 3,6 1,1 0,093 4,4
0,9 0,079 3,8 1,2 0,099 4,7
1 0,080 4,1
Теперь ясно, что на интервале (0,8; 1,2) функция
у = р ( х ) — К ( х ) убывает.
З а д а ч а 17. Вычислите наименьший корень Х о урав
нения
л;2 — ->Jlg х + 100 = 0 (1)
(с относительной погрешностью не более 10“390 %).
Р е ш е н и е . Уравнение (1) определено на [10” 00;
+ оо). Пусть Р ( х ) = х 2 —A f ' g A c + 100. Очевидно,
Р(Ю-юо)> 0; Р( 1 ) < 0 ; />(0,1) <0.
Заменим уравнение (1) равносильным ему уравне
нием л:4 = lg л; + 100. Обозначим: М ( х ) = х F ( x ) =
= l g x + 1 0 0 . Находим М ’ ( х ) = 4x3
t F ’ ( x ) = 1 : ( х In 10).
106](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-108-320.jpg)









![куба пересекают плоскость КРН? Найдите отношение
отрезков, на которые плоскость КРНделит эти ребра.
Р е ш е н и е . Пусть грань ВВ|С|С куба параллельна
плоскости проекции. За направление проектирования
принимаем прямую РК. Получаем параллельную
проекцию куба, на которой отрезок Н изображает
сечение куба плоскостью КРН (рис. 14).
Из этого чертежа ясно, что секущая плоскость
пересекает ребра АВ, ВВ, AD, DD, В|С|, C|D| со
ответственно в точках Я, М Г, К, Р, F, т. е. в сечении
получаем шестиугольник HMPFKT.
На чертеже строим отрезки М/? и НТ| параллельные
отрезку AD. По условию задачи ВР = РС—30 и
KD = 0,25DD = 15. Поэтому ВЕ=Ъ, ££ = 45 и
АЕ = 30. Далее, ВТ .ТЕ = ВН: НА = 2:у т. е. =
= 30 и ТЕ =15.
Из подобия треугольников ВТ'Н и ВЕА получаем
НТ'.АЕ = 2:3 и НТ — 20. Из подобных треугольни
ков МНТ'и имеем: МТМВ = НТ :ВР =
= 20:30 = 2:3, т. е. ВМ.МВ, = 7:3 и МТ = 0У2ВВ] =
= 12, MB = 42, ЕМ= 3.
Из подобных треугольников и PDTследует
iW7’:7 P = £Af:PD = 3:15=1:5, т. е. AT TD = 7:5.
Треугольники и CiPDi подобны. Поэтому
DF:FC = BH.HR = ВТ': ТМ = 30:12 = 5:2.
З а д а ч а 23. Докажите, что во всяком треуголь
нике его медианы пересекаются в одной точке.
Р е ш е н и е . Всякий треугольник„/о можно считать
изображением правильного треугольника. Утверждение
задачи для правильного треугольника верно, потому
что в этом треугольнике медианы являются его бис
сектрисами.
З а д а ч а 24. Дан произвольный треугольник ABC.
ВМ= В А, АК — 4" АС, СР =— СВ. Докажите,
о о 3
что центры тяжестей треугольников ABC и МКРсовпа
дают.
Р е ш е н и е . Треугольник ABC принимаем за изобра
жение правильного треугольника. Тогда и треугольник
МКР будет изображением правильного треугольника.
Центры вращений этих треугольников совпадают.
А так как у правильного треугольника центр вращения
и центр тяжести совпадают, то утверждение задачи
доказано.
З а д а ч а 2 5. Докажите, что в четырехугольнике
J16](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-118-320.jpg)









![Рис. 4 Рис 5
Решив систему этих уравнений, получаем:
fe = 2:3, п =1:6, 77Л,=( 1, -1, -2) и ЯЛ,=Уб.
Ч е т в е р т о е р е ш е н и е . Пусть прямая А|Нпере-
секает плоскость XOYв точке Р(х, у, 0). Тогда
а7Г-ак = 0, (1)
А,Р-АВ=0. (2)
Так как AiP = (x— 1, у — 6, 7); АК = (0, 6, — 3);
АВ i = (6, 6, 0), то уравнения (1) и (2) преобразуются
к виду:
6(у — 6) — 21 = 0, 6(х-1) + 6(*/-6) = 0.
Решив систему этих уравнений, находим Р( —2,5; 9,5;
0). Из прямоугольного треугольника АНА| получаем
(рис. 5):
А [Н= | AiAcos ; АА|Н| = I Л,Л-
А Л ••AiP
|л7р]
1 Жа ЛАхТГ 1
(-2; -4; 4)-(-3,5; 3,5; 7)
Уз,52 + 3,52 + 72
-т/Е
П я т о е р е ш е н и е . Пусть НМ =А Н и М(х,у, г).
Тогда ЛМ2 = ЛЛ], Ш2 = АТ*, BtM2 = Afil По
лучаем ссингему уравнений:
•(х+1)2 + (1/-2)2 + (2 + 3)2 = 36, (1)
(х+1)2 + (у-8)2 + (2 + 6)2 = 9, (2)
. ( х — 5)2 --(у— 8)2 + (z+ З)2 = 36.
1 s
(3)
Выполнив почленное вычитание уравнений (1) из
(3), (2) из (3), получаем:
— 12* + 24 — 12// +60 = 0,
— 12х +24 —6z —27 = 27.
Отсюда у = — х 7 и z = — 2х
нение (1) принимает вид:
(*+1)2 + (-* + 5)2 + (-2*
5. После этого урав-
2)2 = 36.
126](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-128-320.jpg)

















![Из подобных прямоугольных треугольников D}C}E
и DFE получаем DE:DE = DCDF. Отсюда (1 —
— DE):DE = } :( — х) и DE = (1 - х):{2 - х| EDX =
= 1:(2 — х). Очевидно, МН = КЕи НС = ЕС].
Из прямоугольных треугольников МАК, KDEи
EDiCi находим: МК = хл]2; KE=-yJ(1 -
Итак, (2
Р(х) = *д/2 + 2д/( i - х)2 + +
или
р (х) - хд/2 + +-+г[( 1-дг)+1| =
= ХЛ/ 2 + 2 (2 -*) =
хд/2 -(- 2дЛ(2 — x)2 -f-T. (2)
Попытаемся и в этом случае доказать, что Р(х)
меньше периметра диагонального сечения BDD|B|
куба ABCDA[BCD, т. е.
хд/2 + 2 V(2- х)2 +1 < 2 + 2д/2, если 0 < х < 1 . (3)
Еслинеравенство (3) верно, то верны иследую-
щие неравенства (если 0 < * < С 1 ) :
2д/(2 -х)2 + 1 < (2 + 2д/2) - хд/2;
4(4 —4х + х2 + 1 )<(2 + 2д/2)2 — 2х(2 +
2д/2~)д/2 -|- 2х2;
х2-2х(2-72) + (4-4д/2)<0. (4)
Находим корни уравнения, соответствующего нера
венству (4):
х=2 —2Л[2 *2 = 2.
Так как 2 —2д//2<0 и 2> 1, то неравенство (4)
верно, если 0<х< 1. Поэтому доказано и неравенство
( 3 ) , если О С х С1.
Мы уже рассмотрели несколько сечений куба. И во
всех этих случаях доказали, что их периметры не пре-
144](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-146-320.jpg)





![является параллелограммом. Для вычисления площади
параллелограмма необходимо знать длины смежных
сторон АК и КС и угол ф — zl А|КС. Из прямоугольных
треугольников КАА | и КВ Сполучаем:
*с~у/|!+(т)’—#-
Известно, что А|С = ~/з. По теореме косинусов из
треугольника К4|С находим:
Л,/(2 + KC2~AiC2 -2 Л1-с.
COS ф 2Л1/С. /сс -д/Тзо" л *
Теперь ясно, что угол А|КСтупой.
Вычисляем:
Sin? = VI -0054=л1 -4=Vi
Sak-cm — Л i/C • /(С sin ф —
— #-#'У 1 —ум-
Задание 14. ТРИГОНОМЕТРИЧЕСКИЕ
У Р А В Н Е Н И Я И НЕРАВЕНСТВА
З а д а ч а 1. Докажите, что все решения уравнения
(2У2 cos 2 5° - 1) tg х°—(2-#ят 2 5°- l) tg 3x° (1)
— целые числа.
Р е ш е н и е . Основной период уравнения (1) равен
180°. Поэтому сначала исследуем это уравнение на
отрезке [ — 90°; 90°].
Преобразуем уравнение (1) к виду:
tg Зх" 2*2 cos 2 5° — 1 /сух
tg 2д/2 sin 25° - 1
При помощи микрокалькулятора получаем:
2д/2 cos 25° - 1 л 8)0034! 08 л 8 (3)
2д/2 sin 25° - 1
150](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-152-320.jpg)
![Находим:
to- Зл'° ^n лх' 3 sin х" — 4 sin3 х_
° cosЗх" 4 cos3 х°-
n 3 — 4 sin2 х°
4 cos3 х" — 3 cos х" cos х(4 cos2 х"— 3)
о 3 — 4 sin2 х"
sin х°(3 — 4 sin2 х)
— lg-t 4(I----- sin'*')--- 3 —л (4>
(5)
Решив уравнение ( 5 ) , получим:
sin2 лг° ж zo «0,17857142, sin х° « 0,42257711 или
snx° ж—0,42257711. Отсюда *о ~ ±24,997398° ж
ж ±25°.
Выполненные вычисления представляют возмож
ность предположить, что корнями уравнения ( 1 ) , при
надлежащими отрезку [ — 90°; 9 0 ° ] , являются —25°, 0°
и 2 5°.
Проверяем полученную гипотезу. Очевидно, 0°
является решением уравнения (1 ).
Пусть х° — 2 5°. Докажем справедливость равенства
(2д/2 • cos 25° — 1)tg 25° —(2-/2sin250 — l)tg 75°. (1)
Если равенство (1) верно, то
(2д/2 • cos 25° — l)sin 25° cos 75° —
— (2д/2 sin 25° — 1) sin 75° cos 25°;
2 д/2 • cos 25° sin 25° cos 75° — 2 д/2 sin 25° cos 25° sin 75° —
— sin 25° cos 75° — sin 75° cos 25°;
д/2 sin 50° cos 75° — д/2 sin 50° sin 75° — — sin 50°;
V2(cos 75° - sin 75°) — -1; 1 —д/2Ып 75° — sin 15°);
Отсюда ясно, что равенство (1) верно.
Так как t g ( - 2 5 ° ) — -tg25° и tg( — 75°) — —tg75°,
то верно и равенство
1 —/j^/2°-2 750os+£-^i-- sin
75° - 15°
1 — д/2. 2—л.0,5.
(2д/2 • cos 2 5° - l) tg( —2 5°) —
— (2д/2 sin 25° - l ) t g ( —75°).
151](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-153-320.jpg)

![П е р в о е р е ш е н и е . Так как функция arcsinx
определена на отрезке [ — 1 ; 1], то функция arcsin2x
определена на отрезке [ — 0,5; 0,5]. Поэтому монотонная
(возрастающая) и непрерывная функция f{x) =
= arcsin 2x + arcsin x определена на отрезке [ — 0,5;
0,5]. Находим:
/( — 0,5) = arcsin(— 1) + arcsin( —0,5) =
Л 2
1Г ~
-Т Я.
/(0,5) = arcsin 1 -f- arcsin 0,5 = 0,5я + у = у я.
Теперь понятно, что уравнение (1) имеет единст
венный корень Ху причем 0<Сх С 0,5.
При помощи микрокалькулятора найдем прибли
женное значение х с точностью до 10" . Для этого
составляем следующую таблицу значений функции
f(x). Заметим, что 1,0471975:
X fix) X №
0 0 0,3279 1,0470982
0,5 2,0943951 0,32735 1,0472834
0,3 0,9481938 0,32733 1,0472093
0,35 1,1329686 0,32732 1,0471723
0,33 1,0571224 0,327325 1,0471908
0,328 1,049692 5 0,327327 1,0471982
0,327 1,0459873 0,3273265 1,0471963
0,3275 1,0478391
О т в е т . х| ж 0,3273227.
В т о р о е р е ш е н и е . Находим косинус от обеих
частей уравнения ( 1 ) :
cos(arcsin 2х+ arcsin х)= cosy.
Отсюда
~] — 4х2 • д/l — х2 — 2х-х = 0,5.
Решив это иррациональное уравнение, получаем:
*.=0,5уЬ *2 = -0,5
Полученное решение нуждается в проверке. Пусть
153](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-155-320.jpg)

![Наименьшее общее кратное чисел я и 1,5я равно Зя.
Поэтому основной период уравнения (1) равен Зя.
Пусть Т = [0; Зя].
Очевидно, х = Оявляется решением уравнения ( 1 ) .
На интервале (-|я; -|-я) функция у = cos -j.x отри
цательна. Поэтому другие корни уравнения (1) сле
дует искать только на интервалах Л0; -g-я) и (-g-я;
3
При помощи микрокалькулятора сначала найдем
приближенные значения корней уравнения ( 1 ) . Для
этого составляем таблицу значений функции f(x) =
= cos2 x— cos—-хна интервалах Л0; -g-я) и (-g-л;
у я ) , т. е. на интервалах ( 0 ° ; 67,5°) и (202,5°; 270°).
..
/«
Пх)
0 0 202,5 0,85355342
3 — 0,00080306 207 0,6893642
6 — 0,00119426 210 0,57635189
9 -0,00261932 213 0,4614465
12 — 0,00448897 216 0,345491 55
15 -0,00667995 219 0,22934931
18 — 0,00903692 222 0,1 1 38931
21 -0,01 137519 225 0,00000002
24 — 0,01312438 228 -0,11145712
27 -0,01512438 231 — 0,21961736
30 — 0,01604446 234 -0,32363903
33 -0,01597149 237 -0,42270819
36 -0,01462203 240 -0,5160445
39 — 0,01170562 243 — 0,60290965
42 -0,00692866 246 — 0,68261345
45 0,00000002 249 -0,75452006
48 0,00936458 252 — 0,81805397
51 0,02143757 255 -0,87270535
54 0,03647455 258 — 0,91803444
57 0,0547098 261 -0,95367586
60 0,07635185 264 -0,97934187
63 0,10157893 267 — 0,99482505
66 0,1305352 270 — 1
67,5 0,14644661
Из таблицы легко усматриваются следующие ги
потезы :
155](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-157-320.jpg)
![1. Корнями уравнения, принадлежащими отрезку
[0; Зя], являются числа: 0; 0,25я; 1,25я. Непосредствен
ная проверка подтверждает эту гипотезу.
2. На интервале А0; улЛ наименьшее значение
функция f(x) достигает в точке х0 ж у, а на интервале
(у я; ) (функция f(x) монотонно убывает. Для про
верки этой гипотезы находим:
f'(x)----- 2 cos х sin х + у sin у х =
■ / . 4 . 4
= — sin 2x4- у sin у х.
Решив уравнение f'(x) = 0, получаем
Итак, решениями уравнения (1) являются числа
3kn 0,25я + 3пл 1,25я + Зят (к, п, т— целые числа).
Задание 15. ЗАДАЧИ НА РАЗВЕРТКАХ
МНОГОГРАННИКОВ
З а д а ч а 1. На рисунке 1 изображена треугольная
пирамида DABC, а на рисунке 2 дана ее развертка.
DH — высота пирамиды. Отрезки DK, DM, DP —
апофемы боковых граней.
Почему на рисунке 2 лежат на одной прямой точки:
Я, Ри £>,; Я, Ми D2; Я, /С и D3?
Выполнив необходимые измерения на развертке и
вычисления, определите (с точностью, которая задается
разверткой): 1) длину высоты DH| 2) величину (в гра
д у с а х ) угла прямой CD с плоскостью ABC; 3) величину
D
156](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-158-320.jpg)








![= MO.AO = h:-yj2 = 4^]3:л=2-^, то tg АКСА =
i
2Тб’
Из трехгранного угла СКАВ находим t g ( p = Л/3:6.
З а д а ч а 7. Основание пирамиды HABCD — квад
рат ABCD, ребро ЯЛ перпендикулярно плоскости осно
вания. АВ = 3, НА = 4. Докажите, что в пирамиду
можно вписать сферу, и найдите ее радиус.
Для сравнения приведем два решения этой задачи.
П е р в о е р е ш е н и е . Сначала найдем радиус сфе
ры. Потом докажем ее существование. Для этого при
меним формулу 3v = = Sr. Очевидно, V = у 3 • 3 • 4 = 12;
ИВ = 5; 3(Л£С£) = 9; S(BAH) = S(HAD) = 0,5 • 3 • 4 =
= 6; S(HBC) = S(HDC) = 0,5 • 3 • 5 = 7,5. Поэтому S =
= 9 + 2 • 6 + 2 • 7,5 = 36. Получаем г — 1.
Плоскости АВН, ЛЯД и ЛВД взаимно перпенди
кулярны. Поэтому точка О, отстоящая на 1 от этих
плоскостей, есть вершина куба АВ’ CD’ ABOD
(рис. 8). Докажем, что точка О отстоит на 1 от пло
скостей НВС и HDC.
Так как прямая В0 параллельна прямой ВС, то
расстояние от точек В| и О до плоскости НВС одина
ково. Плоскости АВН и ВНС перпендикулярны. Поэто
му расстояние от Si до плоскости НВС равно расстоя
нию от В| до прямой ВН.
Таким образом, задача свелась к доказательству
того, что точка В| есть центр окружности, вписанной
в прямоугольный треугольник НАВ. Так как площадь
165](https://image.slidesharecdn.com/vasiyev-140521021007-phpapp01/85/PDF-167-320.jpg)










