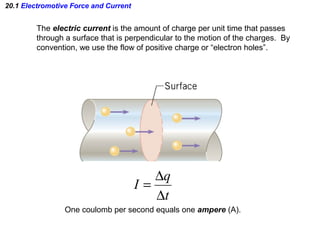
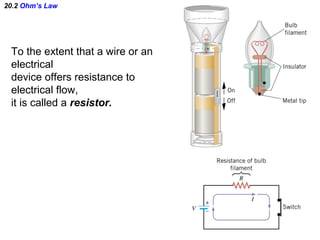
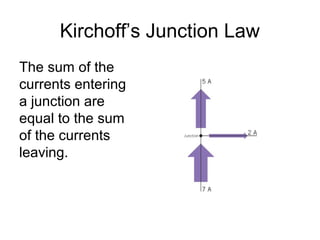
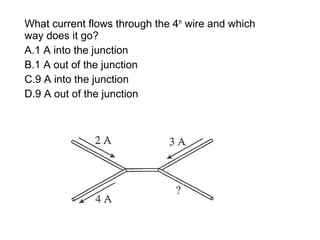
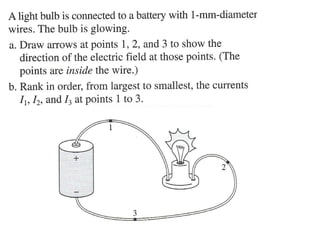
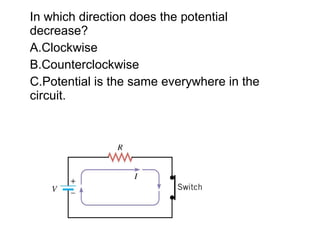
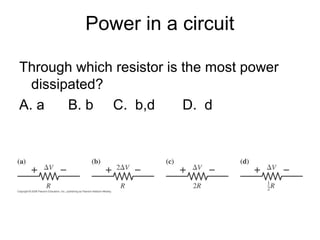
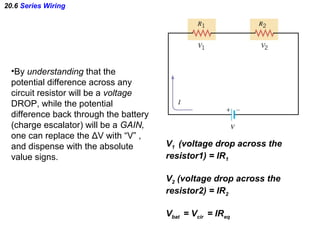
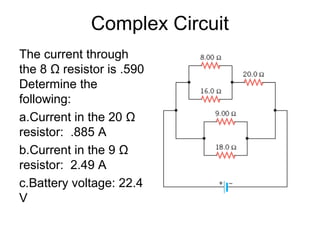
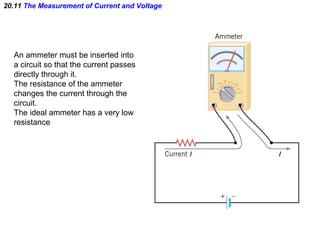
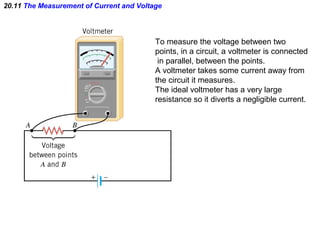
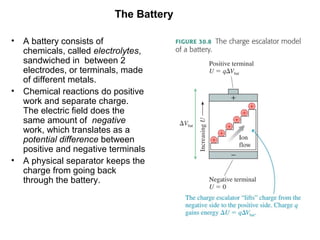
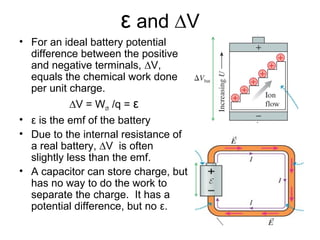
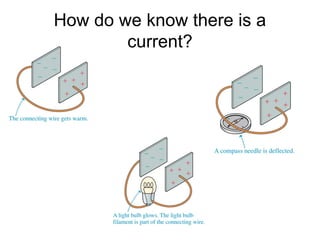
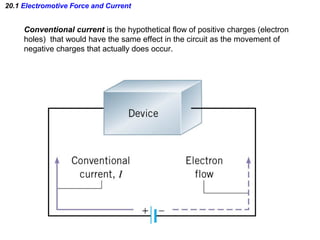
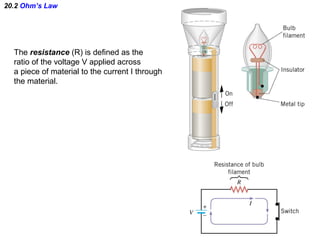
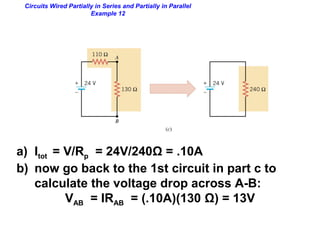
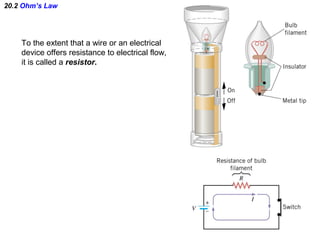
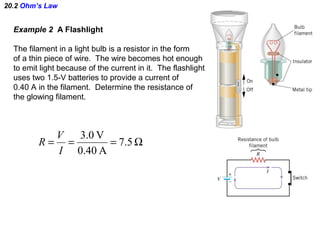
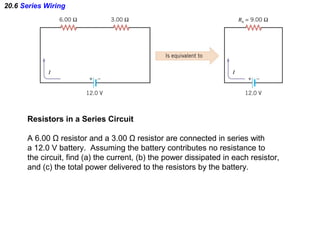
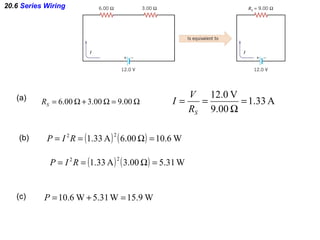
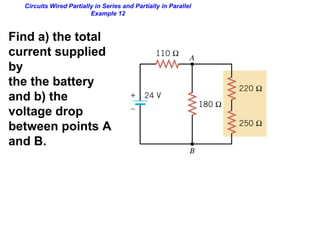
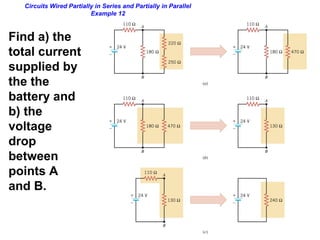
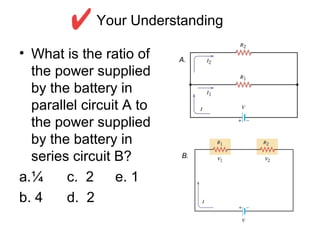
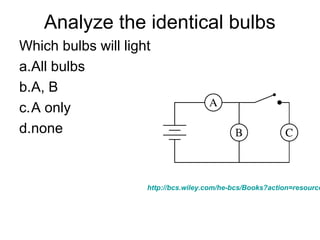
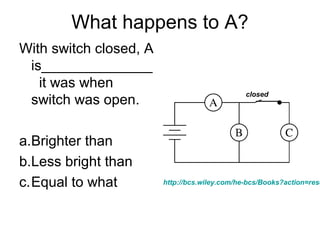
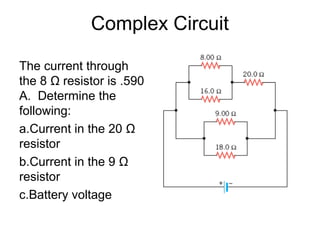
This document discusses electric circuits and Ohm's law. It provides examples of calculating current, resistance, voltage, and power in both series and parallel circuits. Key points covered include: - Ohm's law defines the relationship between voltage, current, and resistance in a circuit. - Components in series experience the same current but their voltages add up. The total resistance is the sum of the individual resistances. 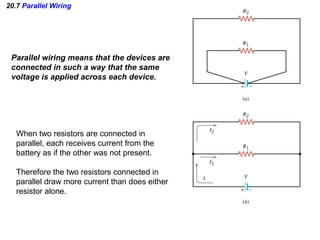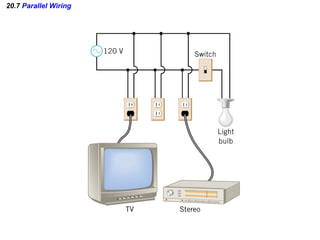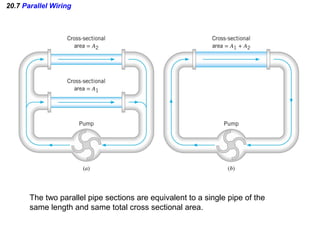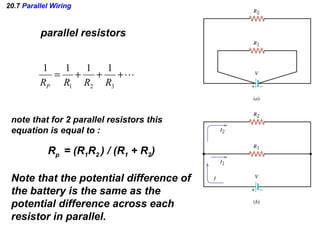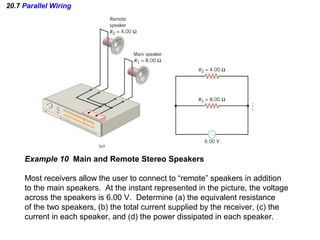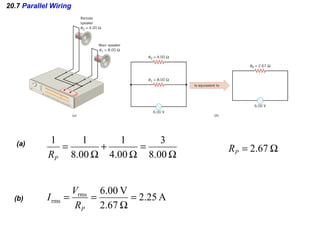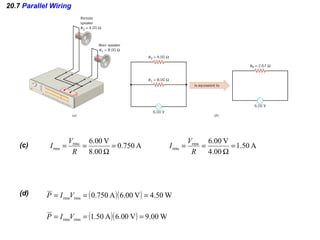- Components in parallel experience the same voltage but their currents combine. The total resistance is lower than any individual resistance. - Power is calculated as the product of voltage and current, and describes how much energy is used by components in a circuit.

1. Electric Circuits

2. Ohm’s Law
The relationship between the potential
difference in a circuit and the resulting
current.
IRVI
R
V
=∆=
∆
or

3. 20.1 Electromotive Force and Current
The electric current is the amount of charge per unit time that passes
through a surface that is perpendicular to the motion of the charges.
http://phet.colorado.edu/en/simulation/signal-circuit

4. 20.1 Electromotive Force and Current
The electric current is the amount of charge per unit time that passes
through a surface that is perpendicular to the motion of the charges. By
convention, we use the flow of positive charge or “electron holes”.
t
q
I
∆
∆
=
One coulomb per second equals one ampere (A).

5. 20.2 Ohm’s Law
To the extent that a wire or an
electrical
device offers resistance to
electrical flow,
it is called a resistor.

6. Kirchoff’s Junction Law
The sum of the
currents entering
a junction are
equal to the sum
of the currents
leaving.

7. What current flows through the 4th
wire and which
way does it go?
A.1 A into the junction
B.1 A out of the junction
C.9 A into the junction
D.9 A out of the junction

9. In which direction does the potential
decrease?
A.Clockwise
B.Counterclockwise
C.Potential is the same everywhere in the
circuit.

10. Ohm’s Law in the Cell
The resistance between the walls of a biological cell is 1.00
x 1010
Ω.
(a)What is the current when the potential difference
between the walls is 95 mV?
(b)If the current is composed of Na+
ions (q = +e), how
much charge moved between the cell walls in 0.2 s?

11. Ohm’s Law in the Cell
Suppose that the resistance between the walls of a
biological cell is 1.00 x 1010
Ω.
(a)What is the current when the potential difference
between the walls is 95 mV? 9.5 x 10-12
A
(b)If the current is composed of Na+
ions (q = +e), how
much charge moved between the cell walls in 0.2 s? 1.9
x 10-12
C

12. Power in a circuit
Through which resistor is the most power
dissipated?
A. a B. b C. b,d D. d

13. Power rating of a household applicance
• Commercial and residential electrical systems are set up
so that each individual appliance operates at a potential
difference of 120 V.
• Power Rating or Wattage is the power that the appliance
will dissipate at a potential difference of 120 V (e.g. 100
W bulb, 1000 W space heater).
• Power consumption will differ if operated at any other
voltage.
• Energy is often expressed as kilowatt-hours, for metering
purposes.

14. kW-h
How much energy in a kilowatt-hour?
A)1000 Joules
B)0.28 Joules
C)3.6 million Joules
D)60,000 Joules

15. Resistors in Series
• Series wiring means that the resistors are connected so that there is
the same current through each resistor.
• The potential difference through each resistor is :
|∆VR |= IR
• The equivalent resistor (Rs ) is made by adding up all resistors in
series in the circuit.
∆Vbat = |∆Vcircuit |= IRs

16. 20.6 Series Wiring
•By understanding that the
potential difference across any
circuit resistor will be a voltage
DROP, while the potential
difference back through the battery
(charge escalator) will be a GAIN,
one can replace the ΔV with “V” ,
and dispense with the absolute
value signs.
V1 (voltage drop across the
resistor1) = IR1
V2 (voltage drop across the
resistor2) = IR2
Vbat = Vcir = IReq

17. 20.6 Series Wiring
Resistors in a Series Circuit
A 6.00 Ω resistor and a 3.00 Ω resistor are connected in series with
a 12.0 V battery. Assuming the battery contributes no resistance to
the circuit, find (a) the current, (b) the power dissipated in each resistor,
and (c) the total power delivered to the resistors by the battery.

18. 20.6 Series Wiring
(a)
(b)
(c)
Ω=Ω+Ω= 00.900.300.6SR A33.1
00.9
V0.12
=
Ω
==
SR
V
I
( ) ( ) W6.1000.6A33.1
22
=Ω== RIP
( ) ( ) W31.500.3A33.1
22
=Ω== RIP
W9.15W31.5W6.10 =+=P

19. Series Resistors
What is the value of R (3rd
resistor in circuit)?
a. 50 Ω b. 25Ω c. 10 Ω d. 0

20. 20.7 Parallel Wiring
Parallel wiring means that the devices are
connected in such a way that the same
voltage is applied across each device.
When two resistors are connected in
parallel, each receives current from the
battery as if the other was not present.
Therefore the two resistors connected in
parallel draw more current than does either
resistor alone.

21. 20.7 Parallel Wiring

22. 20.7 Parallel Wiring
The two parallel pipe sections are equivalent to a single pipe of the
same length and same total cross sectional area.

23. 20.7 Parallel Wiring
parallel resistors
+++=
321
1111
RRRRP
note that for 2 parallel resistors this
equation is equal to :
Rp = (R1R2 ) / (R1 + R2)
Note that the potential difference of
the battery is the same as the
potential difference across each
resistor in parallel.

24. 20.7 Parallel Wiring
Example 10 Main and Remote Stereo Speakers
Most receivers allow the user to connect to “remote” speakers in addition
to the main speakers. At the instant represented in the picture, the voltage
across the speakers is 6.00 V. Determine (a) the equivalent resistance
of the two speakers, (b) the total current supplied by the receiver, (c) the
current in each speaker, and (d) the power dissipated in each speaker.

25. 20.7 Parallel Wiring
(a)
Ω
=
Ω
+
Ω
=
00.8
3
00.4
1
00.8
11
PR
Ω= 67.2PR
(b) A25.2
67.2
V00.6rms
rms =
Ω
==
PR
V
I

26. 20.7 Parallel Wiring
A750.0
00.8
V00.6rms
rms =
Ω
==
R
V
I(c) A50.1
00.4
V00.6rms
rms =
Ω
==
R
V
I
(d) ( )( ) W50.4V00.6A750.0rmsrms === VIP
( )( ) W00.9V00.6A50.1rmsrms === VIP

27. Circuits Wired Partially in Series and Partially in Parallel
Example 12
Find a) the total
current supplied
by
the the battery
and b) the
voltage drop
between points A
and B.

28. Circuits Wired Partially in Series and Partially in Parallel
Example 12
Find a) the
total current
supplied by
the the
battery and
b) the
voltage
drop
between
points A
and B.

29. Circuits Wired Partially in Series and Partially in Parallel
Example 12
a) Itot = V/Rp = 24V/240Ω = .10A
b) now go back to the 1st circuit in part c to
calculate the voltage drop across A-B:
VAB = IRAB = (.10A)(130 Ω) = 13V

30. Your Understanding
• What is the ratio of
the power supplied
by the battery in
parallel circuit A to
the power supplied
by the battery in
series circuit B?
a.¼ c. 2 e. 1
b. 4 d. 2
A.
B.

31. Analyze the identical bulbs
Which bulbs will light
a.All bulbs
b.A, B
c.A only
d.none
http://bcs.wiley.com/he-bcs/Books?action=resource

32. What happens to A?
With switch closed, A
is______________
it was when
switch was open.
a.Brighter than
b.Less bright than
c.Equal to what http://bcs.wiley.com/he-bcs/Books?action=reso
closed

33. Complex Circuit
The current through
the 8 Ω resistor is .590
A. Determine the
following:
a.Current in the 20 Ω
resistor
b.Current in the 9 Ω
resistor
c.Battery voltage

34. Complex Circuit
The current through
the 8 Ω resistor is .590
Determine the
following:
a.Current in the 20 Ω
resistor: .885 A
b.Current in the 9 Ω
resistor: 2.49 A
c.Battery voltage: 22.4
V

35. 20.11 The Measurement of Current and Voltage
An ammeter must be inserted into
a circuit so that the current passes
directly through it.
The resistance of the ammeter
changes the current through the
circuit.
The ideal ammeter has a very low
resistance

36. 20.11 The Measurement of Current and Voltage
To measure the voltage between two
points, in a circuit, a voltmeter is connected
in parallel, between the points.
A voltmeter takes some current away from
the circuit it measures.
The ideal voltmeter has a very large
resistance so it diverts a negligible current.

37. • A battery consists of
chemicals, called electrolytes,
sandwiched in between 2
electrodes, or terminals, made
of different metals.
• Chemical reactions do positive
work and separate charge.
The electric field does the
same amount of negative
work, which translates as a
potential difference between
positive and negative terminals
• A physical separator keeps the
charge from going back
through the battery.
The Battery

38. ε and ∆V
• For an ideal battery potential
difference between the positive
and negative terminals, ∆V,
equals the chemical work done
per unit charge.
∆V = Wch /q = ε
• ε is the emf of the battery
• Due to the internal resistance of
a real battery, ∆V is often
slightly less than the emf.
• A capacitor can store charge, but
has no way to do the work to
separate the charge. It has a
potential difference, but no ε.

39. How do we know there is a
current?

40. 20.1 Electromotive Force and Current
If the charges move around the circuit in the same direction at all times,
the current is said to be direct current (dc).
If the charges move first one way and then the opposite way, the current is
said to be alternating current (ac).

41. EOC #3
A fax machine uses 0.110 A of current in its normal mode
of operation, but only 0.067 A in the standby mode. The
machine uses a potential difference of 120 V.
(a)In one minute (60 s!), how much more charge passes
through the machine in the normal mode than in the
standby mode?
(b)How much more energy is used?

42. EOC #3
A fax machine uses 0.110 A of current in its normal mode
of operation, but only 0.067 A in the standby mode. The
machine uses a potential difference of 120 V.
(a)In one minute (60 s!), how much more charge passes
through the machine in the normal mode than in the
standby mode? .043 C/s x 60 s = 2.6 C
(b)How much more energy is used? 2.58 C x 120 J/C = 310
J

43. 20.1 Electromotive Force and Current
Conventional current is the hypothetical flow of positive charges (electron
holes) that would have the same effect in the circuit as the movement of
negative charges that actually does occur.

44. 20.2 Ohm’s Law
The resistance (R) is defined as the
ratio of the voltage V applied across
a piece of material to the current I through
the material.

45. 20.2 Ohm’s Law
To the extent that a wire or an electrical
device offers resistance to electrical flow,
it is called a resistor.

46. 20.2 Ohm’s Law
Example 2 A Flashlight
The filament in a light bulb is a resistor in the form
of a thin piece of wire. The wire becomes hot enough
to emit light because of the current in it. The flashlight
uses two 1.5-V batteries to provide a current of
0.40 A in the filament. Determine the resistance of
the glowing filament.
Ω=== 5.7
A0.40
V0.3
I
V
R