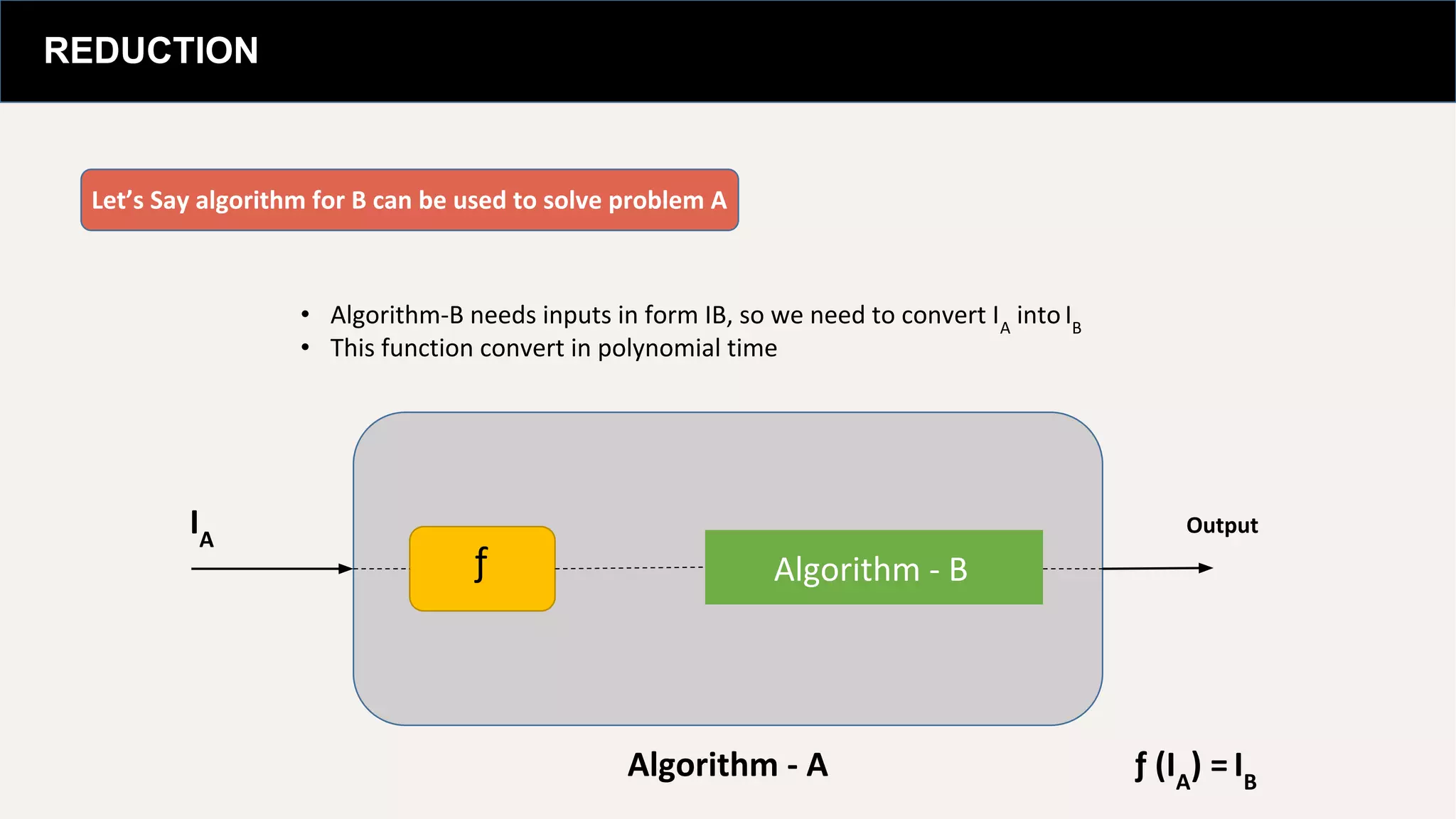
NP-hard problems are those that can be solved if there exists an NP-complete problem that can be reduced to them in polynomial time. Various algorithms can handle these problems, including reductions that convert one problem's instance into another for solution. Applications of NP-hard problems include areas like cryptography, scheduling, and data mining, with examples like the traveling salesman problem highlighting their complexity.

1. NP-Hard
❑NP-Hard problems(say X) can be solved if and only if there is a
NP-Complete problem(say Y) that can be reducible into X in
polynomial time.
❑To solve this problem, it do not have to be in NP .
❑Do not have to be a Decision problem.
❑Example: Halting problem, Vertex cover problem, etc.
Definition

2. Polynomial Time Algorithms
Linear Search n
Binary search Log(n)
Insertion sort
Merge sort nlog(n)
Matrix multiplication
Non-Polynomial Time Algorithms
0/1 knapsack problem
TSP
Sum of subset
Graph coloring
Hamiltonian Cycle

3. REDUCTION
Problem - A Problem - B
Input : IA
Input : IB
Algorithm - A Algorithm - B
Let’s Say algorithm for B can be used to solve problem A

4. REDUCTION
Let’s Say algorithm for B can be used to solve problem A
• Algorithm-B needs inputs in form IB, so we need to convert IA
into IB
• This function convert in polynomial time
Algorithm - B
ƒ
IA
Output
Algorithm - A ƒ (IA
) = IB

5. REDUCTION
Problem - A Problem - B
A≤ B
Problem A is Reducible to problem B, if there is function which convert
instance of A into instance of B and solution of that instance provide
solution to problem A.
Cost = Conversion Cost + algorithm B Cost
= Polynomial + Algorithm B Cost

6. Applications
• Approximate computing
• Configuration
• Cryptography
• Data mining
• Decision support
• Phylogenetics
• Planning
• Process monitoring and control
• Rosters or schedules
• Routing/vehicle routing
• Scheduling
NP-hard problems are often tackled with rules-based languages in areas including:

7. Data Mining
Data mining is the process of sorting through large data sets to identify
patterns and relationships that can help solve business problems
through data analysis.

8. Travelling salesman problem
The TSP is classified as NP-hard because it has no “quick” solution and
the complexity of calculating the best route will increase when you add
more destinations to the problem.

9. Routing/vehicle routing
Routing represents the entire process of planning delivery routes for
the vehicles in a fleet. The goal is to create the most cost-effective
route by minimizing the distance and traveled time necessary to reach
a set of planned stops.