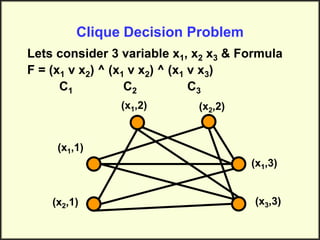
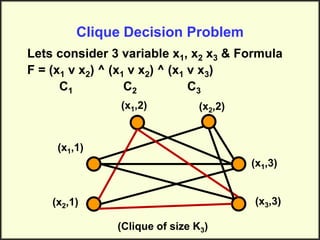
This document discusses NP-hard and NP-complete problems. It begins by describing problems that have an exponential upper bound but a polynomial lower bound, suggesting they are intractable though tractability is also possible. NP-complete problems share this property and are all reducible to each other. Examples of NP-complete problems discussed include the traveling salesman problem, map coloring, and scheduling problems. The clique decision problem is then described and an example is worked through to show finding a clique of size 3, demonstrating it is NP-hard. Finally, it is noted that if an algorithm can be found for an NP-hard problem, it becomes NP-complete.

1. Topic
NP- Hard/NP-Complete Problems
Zohra Naim- M77
Mehwish Basheer- M29

2. Problems that Cross the Line
• What if a problem has:
– An exponential upper bound
– A polynomial lower bound
• We have only found exponential algorithms, so it
appears to be intractable.

3. NP-Complete Problems
• The upper bound suggests the
problem is intractable
• The lower bound suggests the
problem is tractable
• The lower bound is linear: O(N)
• They are all reducible to each other
– If we find a reasonable algorithm
(or prove intractability) for one,
then we can do it for all of them!

4. Example NP-Complete Problems
• Path-Finding (Traveling salesman)
• Map coloring
• Scheduling and Matching (bin packing)
• 2-D arrangement problems
• Planning problems (pert planning)
• Clique

5. Traveling Salesman

6. 5-Clique

7. Map Coloring

8. Class Scheduling Problem
• With N teachers with certain hour
restrictions M classes to be scheduled,
can we:
– Schedule all the classes
– Make sure that no two teachers teach
the same class at the same time
– No teacher is scheduled to teach two
classes at once

9. Certificates
• Returning true: in order to show that the
schedule can be made, we only have to
show one schedule that works
– This is called a certificate.
• Returning false: in order to show that
the schedule cannot be made, we must
test all schedules.

10. Determinism vs. Nondeterminism
• Nondeterministic algorithms produce an
answer by a series of “correct guesses”
• Deterministic algorithms (like those that a
computer executes) make decisions
based on information.

11. NP-Complete
“NP-Complete” comes from:
– Nondeterministic Polynomial
– Complete - “Solve one, Solve them all”
There are more NP-Complete problems than
provably intractable problems.

12. NP-Complete
for any NP-Complete problem:
– Raise the lower bound
(via a stronger proof)
– Lower the upper bound
(via a better algorithm)

13. Clique Decision Problem
1. Lets consider 3 variable x1, x2 x3 & Formula
2. F = (x1 v x2) ^ (x1 v x2) ^ (x1 v x3) then assign classes
1. C1 C2 C3
3. Plot the points for each class w.r variables
4. Connect the points in such a way that the variables
i.e x1 and its bar x1 can not be connected.
5. Find the max clique size i.e ki
6. Check if the problem can be solved

14. Clique Decision Problem
Lets consider 3 variable x1, x2 x3 & Formula
F = (x1 v x2) ^ (x1 v x2) ^ (x1 v x3)
C1 C2 C3
(x1,1)
(x2,1)
(x1,2) (x2,2)
(x1,3)
(x3,3)

15. Clique Decision Problem
Lets consider 3 variable x1, x2 x3 & Formula
F = (x1 v x2) ^ (x1 v x2) ^ (x1 v x3)
C1 C2 C3
(x1,1)
(x2,1)
(x1,2) (x2,2)
(x1,3)
(x3,3)

16. Clique Decision Problem
Lets consider 3 variable x1, x2 x3 & Formula
F = (x1 v x2) ^ (x1 v x2) ^ (x1 v x3)
C1 C2 C3
(x1,1)
(x2,1)
(x1,2) (x2,2)
(x1,3)
(x3,3)
(Clique of size K3)

17. Clique Decision Problem
Lets consider 3 variable x1, x2 x3 & Formula
F = (x1 v x2) ^ (x1 v x2) ^ (x1 v x3)
C1 C2 C3
(x1,1)
(x2,1)
(x1,2) (x2,2)
(x1,3)
(x3,3)
Now
x1 x2 x3
0 1 1
1 = true
O = false
(Clique of size K3)

18. Clique Decision Problem
0 or 1 1 or 0 0 or 1
F = (x1 v x2) ^ (x1 v x2) ^ (x1 v x3)
C1 = 1 C2 = 1 C3 = 1
C1^C2^C3 = 1^1^1= 1
• Hence proved that CDP is a NP-Hard problem
• If we can make its algorithm successfully then it
will be called NP- Complete
x1 x2 x3
0 1 1
1 = true
O = false

19. Questions?