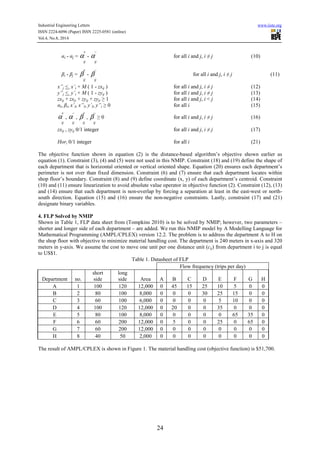
This paper introduces a new mixed integer programming (NMIP) approach for solving the Facility Layout Problem (FLP), aimed at optimizing departmental placements while accommodating unequal dimensions. The NMIP formulation addresses limitations of classic mixed integer programming by eliminating certain parameters that often lead to infeasibility in real-world applications, enhancing practicality for facility layout design. Extensive testing on existing problems demonstrates that NMIP effectively minimizes material handling costs, achieving a significant reduction in overall operational expenses.