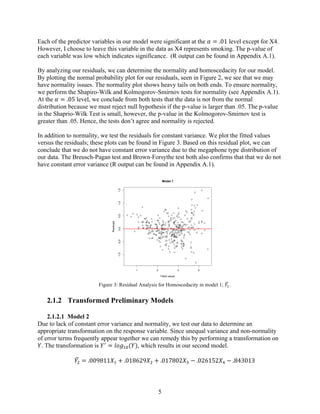
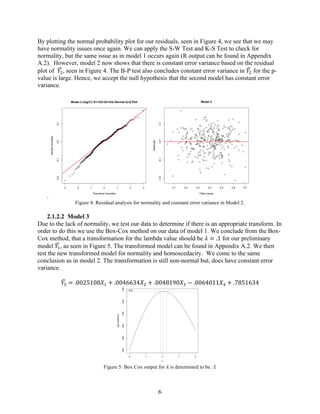
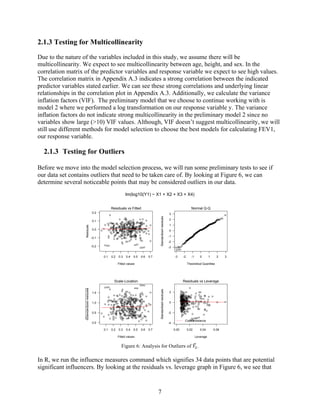
1) The document describes analyzing a dataset containing measurements from 654 youth to build a regression model for predicting forced expiratory volume (FEV1) based on age, height, sex, and smoking status. 2) The preliminary model showed issues with non-normality and non-constant variance. Various transformations were tested, with the best being a log transformation of FEV1 (model 2). 3) Tests for multicollinearity and outliers were also run, with some correlation between predictors but no significant outliers found that required removal from the dataset.

1. 1
Forced Expiratory Volume Regression Model
Katie Ruben
February 29, 2016
Forced expiratory volume (FEV1) is the volume of air forcibly expired in the first second of
maximal expiration after a maximal inspiration. FEV1 is a significant parameter for identifying
restrictive and obstructive respiratory diseases like asthma. It is a useful measure of how quickly
full lungs can be emptied. A common clinical technique to measure this quantity is through
Spirometry. Spirometry measures the rate at which the lung changes volume. The volume of the
capacity of a lung is measured in liters. Results received from a spirometry test are dependent on
the effort and cooperation between patients and examiners. These results depend heavily on the
technicality of implementation as well as personal attributes of the patient [2]. Personal attributes
that will help determine an accurate FEV1 score will be the patient's age, height, sex, and
indication of being a smoker or non-smoker.
The data used during this simulation comes from the Journal of Statistics Education Archive [3].
The data set consists of 4 variables, some of which are directly measured and some that are
qualitative in nature.
The data set is composed of a sample population consisting of 654 youth, male and female, aged
between 3 and 19 years old from the East Boston area in the late 1970’s [5]. This data set
contains 4 variables of measurement of children including age (years), height (inches), sex
(male/female), and their self indication about being a smoker (yes/no). An investigation of the
relationship between a child’s FEV1 and their current smoking status will be sought. It is
important to note that the younger the child, the lower their FEV1 lung capacity will be due to
the stature of their body alone. Therefore, in a normal case, the older the child is, the higher the
lung capacity as their body grows.
Another good measure of lung capacity is looking at the ratio between FEV1 and FVC. Forced
vital capacity (FVC) is the maximum total volume of air expired after a maximal deep breath in,
which takes 6 seconds to fully expire. A normal ratio value for a person without pulmonary
obstruction is between 80% and 120% [1]. A percentage lower than 80% is indicative of
obstructive lung functions. Since a predicted FVC value is not provided in the data set, one could
use known formulas to calculate this value for male and female children based off of their
personal attributes [4]. However, in using the data provided to calculate the predicted FVC value
will result in using the parameters for each child twice. Once in the predicted FVC formula and
once again when I perform a regression analysis. This would not be a good idea. Therefore, I will
exclude the the FEV1 to FVC ratio from my analysis, but it is good background information in
interpreting a person’s lung function.
In order to analyze this data, I will use our predictor variables to construct a linear regression
model for predicting FEV1 values. Upon initial fittings, I will analyze the model and look for
any initial predicting issues. Additionally, I will interpret the analysis of the data in order to

2. 2
describe the meaning of FEV1 to each of the predictor variables dependent on the multiple
regression model chosen. I can determine the correlation between each of the predictor variables
and my regression fittings by looking at plots of each predictor variable and the fitted FEV1
calculated. Additionally, I can compute the correlation matrix to begin an initial evaluation of
strongly correlated variables in the data. I will look into determining if there are any
multicollinearity problems in our data. After determining the most necessary and possibly
unnecessary variables, I will try to find an appropriate regression model for the predictor
variables provided in the data set. Further, I will test for any possible outliers in the data that
would be significantly influencing the regression. In the case that we find significant outliers, I
will remove this data and try to create a new regression.
In this analysis of data, I will use multiple regression techniques to try to find the best fit for our
given data set. We will test for multicollinearity problems, the significance of our regression
coefficients, and assess for possible outliers.

3. 3
1 Background
Forced expiratory volume (FEV1) is the volume of air forcibly expired in the first second of
maximal expiration after a maximal inspiration. FEV1 is a significant parameter for identifying
restrictive and obstructive respiratory diseases like asthma. It is a useful measure of how quickly,
full lungs can be emptied. A common clinical technique to measure this quantity is through
Spirometry. Spirometry measures the rate at which the lung changes volume. The volume of the
capacity of a lung is measured in liters. Results received from a spirometry test are dependent on
the effort and cooperation between patients and examiners. These results depend heavily on the
technicality of implementation as well as personal attributes of the patient [2]. Personal attributes
that will help determine an accurate FEV1 score will be the patient's age, height, sex, and
indication of being a smoker or non-smoker.
VARIABLE DESCRIPTION
𝒀 FEV1 (liters)
𝑿 𝟏 Age (years)
𝑿 𝟐 Height (inches)
𝑿 𝟑 Sex (male or female)
𝑿 𝟒 Smoker (yes or no)
Table 1: Variable Descriptions
For our model prediction analysis, we use a data set containing four variables. This data set is
from The Journal of Statistical Education and publically shared by Michael Kahn [3] with the
approval of Bernard Rosner who published the data in 1999 in Fundamentals of Biostatistics [5].
The data set is composed of a sample population consisting of 654 youth, male and female, aged
between 3 and 19 years old from the East Boston area in the late 1970’s. An investigation of the
relationship between a child’s FEV1 and their current smoking status will be sought as well as
any other comparisons between predictor variables. The variable descriptions can be found in
table 1. The indication of smoking for predictor variable 𝑋4, is qualitative data about each child.
The child made an indication if they, themselves were smokers or not while the data was being
collected.
It is important to note that the younger the child, the lower their FEV1 lung capacity will be due
to the stature of their body alone. Therefore, in a normal case, the older the child is, the higher
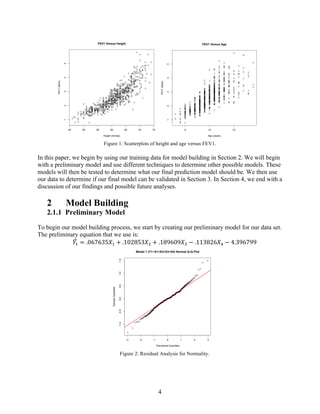
the lung capacity as their body grows. As seen in Figure 1, the taller the child is then the higher
their FEV1. In addition, Figure 1 shows that in general as the child gets older their FEV1
increase however further investigation is needed into the interpretation of the FEV1 versus age
scatterplot. There may exist other factors that result in a drop of FEV1 as the children reach
puberty. We aim to find our best linear regression model for predicting FEV1 based off of our
four predictor variables; age, height, sex, and indication of smoking. In our model building
process we will want to determine if we can predict FEV1 using less measurements.

4. 4
Figure 1: Scatterplots of height and age versus FEV1.
In this paper, we begin by using our training data for model building in Section 2. We will begin
with a preliminary model and use different techniques to determine other possible models. These
models will then be tested to determine what our final prediction model should be. We then use
our data to determine if our final model can be validated in Section 3. In Section 4, we end with a
discussion of our findings and possible future analyses.
2 Model Building
2.1.1 Preliminary Model
To begin our model building process, we start by creating our preliminary model for our data set.
The preliminary equation that we use is:
𝑌* = .067635𝑋* + .102853𝑋6 + .189609𝑋8 − .113826𝑋: − 4.396799
Figure 2: Residual Analysis for Normality.
45 50 55 60 65 70 75
12345
FEV1 Versus Height
Height (inches)
FEV1(liters)
5 10 15
12345
FEV1 Versus Age
Age (years)
FEV1(liters)
-3 -2 -1 0 1 2 3
-1.0-0.50.00.51.01.5
Model 1 (Y1~X1+X2+X3+X4) Normal Q-Q Plot
Theoretical Quantiles
SampleQuantiles

5. 5
Each of the predictor variables in our model were significant at the 𝛼 = .01 level except for X4.
However, I choose to leave this variable in the data as X4 represents smoking. The p-value of
each variable was low which indicates significance. (R output can be found in Appendix A.1).
By analyzing our residuals, we can determine the normality and homoscedacity for our model.
By plotting the normal probability plot for our residuals, seen in Figure 2, we see that we may
have normality issues. The normality plot shows heavy tails on both ends. To ensure normality,
we perform the Shapiro-Wilk and Kolmogorov-Smirnov tests for normality (see Appendix A.1).
At the 𝛼 = .05 level, we conclude from both tests that the data is not from the normal
distribution because we must reject null hypothesis if the p-value is larger than .05. The p-value
in the Shaprio-Wilk Test is small, however, the p-value in the Kolmogorov-Smirnov test is
greater than .05. Hence, the tests don’t agree and normality is rejected.
In addition to normality, we test the residuals for constant variance. We plot the fitted values
versus the residuals; these plots can be found in Figure 3. Based on this residual plot, we can
conclude that we do not have constant error variance due to the megaphone type distribution of
our data. The Breusch-Pagan test and Brown-Forsythe test both also confirms that that we do not
have constant error variance (R output can be found in Appendix A.1).
Figure 3: Residual Analysis for Homoscedacity in model 1; 𝑌*.
2.1.2 Transformed Preliminary Models
2.1.2.1 Model 2
Due to lack of constant error variance and normality, we test our data to determine an
appropriate transformation on the response variable. Since unequal variance and non-normality
of error terms frequently appear together we can remedy this by performing a transformation on
𝑌. The transformation is 𝑌<
= 𝑙𝑜𝑔*@(𝑌), which results in our second model.
𝑌6 = .009811𝑋* + .018629𝑋6 + .017802𝑋8 − .026152𝑋: − .843013
1 2 3 4
-1.0-0.50.00.51.01.5
Model 1
Fitted values
Residuals

6. 6
By plotting the normal probability plot for our residuals, seen in Figure 4, we see that we may
have normality issues once again. We can apply the S-W Test and K-S Test to check for
normality, but the same issue as in model 1 occurs again (R output can be found in Appendix
A.2). However, model 2 now shows that there is constant error variance based on the residual
plot of 𝑌6, seen in Figure 4. The B-P test also concludes constant error variance in 𝑌6 for the p-
value is large. Hence, we accept the null hypothesis that the second model has constant error
variance.
.
Figure 4: Residual analysis for normality and constant error variance in Model 2.
2.1.2.2 Model 3
Due to the lack of normality, we test our data to determine if there is an appropriate transform. In
order to do this we use the Box-Cox method on our data of model 1. We conclude from the Box-
Cox method, that a transformation for the lambda value should be 𝜆 = .1 for our preliminary
model 𝑌*, as seen in Figure 5. The transformed model can be found in Appendix A.2. We then
test the new transformed model for normality and homoscedacity. We come to the same
conclusion as in model 2. The transformation is still non-normal but, does have constant error
variance.
𝑌8 = .0025108𝑋* + .0046634𝑋6 + .0048190𝑋8 − .0064011𝑋: + .7851634
Figure 5: Box Cox output for 𝜆 is determined to be . 1
-3 -2 -1 0 1 2 3
-0.2-0.10.00.1
Model 2 (log(Y)~X1+X2+X3+X4) Normal Q-Q Plot
Theoretical Quantiles
SampleQuantiles
0.1 0.2 0.3 0.4 0.5 0.6 0.7
-0.2-0.10.00.1
Model 2
Fitted values
Residuals
-2 -1 0 1 2
-550-500-450-400-350-300
λy
log-Likelihood
95%

7. 7
2.1.3 Testing for Multicollinearity
Due to the nature of the variables included in this study, we assume there will be
multicollinearity. We expect to see multicollinearity between age, height, and sex. In the
correlation matrix of the predictor variables and response variable we expect to see high values.
The correlation matrix in Appendix A.3 indicates a strong correlation between the indicated
predictor variables stated earlier. We can see these strong correlations and underlying linear
relationships in the correlation plot in Appendix A.3. Additionally, we calculate the variance
inflation factors (VIF). The preliminary model that we choose to continue working with is
model 2 where we performed a log transformation on our response variable y. The variance
inflation factors do not indicate strong multicollinearity in the preliminary model 2 since no
variables show large (>10) VIF values. Although, VIF doesn’t suggest multicollinearity, we will
still use different methods for model selection to choose the best models for calculating FEV1,
our response variable.
2.1.3 Testing for Outliers
Before we move into the model selection process, we will run some preliminary tests to see if
our data set contains outliers that need to be taken care of. By looking at Figure 6, we can
determine several noticeable points that may be considered outliers in our data.
Figure 6: Analysis for Outliers of 𝑌6.
In R, we run the influence measures command which signifies 34 data points that are potential
significant influencers. By looking at the residuals vs. leverage graph in Figure 6, we see that
0.1 0.2 0.3 0.4 0.5 0.6 0.7
-0.2
-0.1
0.0
0.1
0.2
Fitted values
Residuals
Residuals vs Fitted
224
323 44
-3 -2 -1 0 1 2 3
-3
-2
-1
0
1
2
3
Theoretical Quantiles
Standardizedresiduals
Normal Q-Q
224
32344
0.1 0.2 0.3 0.4 0.5 0.6 0.7
0.0
0.5
1.0
1.5
Fitted values
Standardizedresiduals
Scale-Location
224
323 44
0.00 0.02 0.04 0.06
-4
-2
0
2
Leverage
Standardizedresiduals
Cook's distance
Residuals vs Leverage
44323
224
lm(log10(Y1) ~ X1 + X2 + X3 + X4)

8. 8
point 323, 44, and 224 are labeled values. Note that the scale on the leverage axis is extremely
small. Hence, in reality none of these data points are truly that far apart in order to skew our
regression model. I will test these three values using the influence measures of DEFITS, Cook’s
Distance, H-matrix, and DFBETA.
n DEFITS Cook’s
Distance
Hat
Matrix
DFBETA
Intercept
DFBETA
X1
DFBETA
X2
DFBETA
X3
DFBETA
X4
323 -0.53721 5.62e-02 0.02865 -3.94e-01 -1.17e-02 3.16e-01 -2.51e-01 -1.05e-01
224 -0.51478 5.12e-02 0.02091 0.02865 -3.46e-03 -2.71e-01 2.75e-01 2.10e-01
44 -0.55968 6.12e-02 0.03405 1.21e-01 1.14e-01 -1.39e-01 1.52e-01 -4.51e-01
Table 1: Potential Outliers
If the DEFITS value is greater than 1, we conclude that the point is influential. Above, these
three points are not influential according to this criterion.
In order to assess influential points based off of the COOKS distance, I will need to find the F-
distribution for 𝐹 5,327 − 5 = 𝐹(5,322) for each of the COOK values. If the percentile value
is less than 10 or 20 percent, then the case has little apparent influence on the fitted values. When
n=323, we get that .0562 is the .2th
percentile of the distribution. When n=224, we get that .0512
is the .16th
percentile of the distribution. When n=44, we get that .0612 is the .25th
percentile of
the distribution. Since all of these percentile values are less than 10 or 20 percent, we conclude
again that these cases are non-influential.
In order to assess if outliers exists in relation to the ℎGG, I will look to see if ℎGG >
6I
J
. If this
occurs then it suggests that the value corresponding to ℎGG may be an outlier. In this data set,
6I
J
=
6∗L
86M
= .030581. Based on the cases of interest in the chart above, we see that case 44 would
be considered an outlier. However, the other influence measures do not suggest this point as an
outlier.
In order to assess influential points based off of DFBETAS we look to see if the
absolute value of number presented for each case exceeds 1. If it exceeds 1 then that case might
be an influential point. Again, none of these points leads to an outlier.
The code used in R to get the output for this list of influential measures is located in Appendix
A.1. The additional, potential influential points can be assessed by looking at the code.
2.2 Model Selection
Now we will use multiple methods to determine possible subsets of predictor variables to use in
a new model based off of preliminary model 2. We will discuss our selection methods and new
potential models below.

9. 9
Using R’s leaps package, we can find appropriate subsets to use for model prediction. Using the
scale of CP Mallow values, shown in Appendix A.4, we find the same best possible subset of
variables as presented in 𝑌6. Thus, we look for other model selections.
We use the same method but, use adjusted R-squared scale to determine the subset collection
now (shown in Appendix A.4). This method yields the subsets {𝑋*, 𝑋6}, {𝑋*, 𝑋6, 𝑋8, }, and
{𝑋*, 𝑋6, 𝑋:}. Note, that all three of these subsets have the same adjusted R-squared value. I want
to find multiple subsets of prediction models to compare which model is better. Using these two
new subsets, we get the following three new models:
𝑌6,* =. 0079265𝑋*+.0192128𝑋6 − .8537001
𝑌6,6 =. 0090268𝑋* + .0192252𝑋6 − .0293616𝑋: − .8623788
𝑌6,8 =. 0089099𝑋* + .0185659𝑋6 + .0193566𝑋8 − .8336753
In addition, we used the forward and backward AIC stepwise method in R. The model that we
come up with in R has the same subset of variables as presented in 𝑌6. This can be seen in the R
output in Appendix A.4. Since, our data set only contains four variables, this is not uncommon
for the predicted model to be the same as our preliminary model if all of the variables are
important to the calculation of the response.
With each method, we have varying subsets of predictor variables. In order to determine the best
model, we compute 𝑅QRS
6
, 𝑉𝐼𝐹, 𝐴𝐼𝐶, 𝐵𝐼𝐶, and PRESS for each model. We aim to find a model
with the smallest 𝑉𝐼𝐹, 𝐴𝐼𝐶, 𝐵𝐼𝐶, and PRESS as well as the largest 𝑅QRS
6
; these values are
highlighted in the Table 2.
Model 𝑅QRS
6
𝑉 𝐼𝐹 𝐴𝐼𝐶 𝐵𝐼𝐶 𝑃𝑅𝐸𝑆𝑆
𝑌6 .813 1.941479 -1813.209 -1794.259 1.280946
𝑌6,* .8072 2.561182 -1805.266 -1793.896 1.309714
𝑌6,6 .8099 2.150455 -1808.889 -1793.73 1.297981
𝑌6,8 .811 2.144651 -1810.701 -1795.541 1.288214
Table 2: Four potential FEV1 Models
As seen in the Table 2, each model yields around the same 𝑅QRS
6
. From the mean VIF values, we
see that there is no serious multicollinearity problem since no values are greater than 10.
Additionally, the AIC and BIC values for each model do not vary significantly. From the table,
we see that 𝑌6 appears to be the best in four of the five tests performed in Table 2. Thus, we will
use this as our final FEV1 model. This model is the transformed preliminary model we had
initial constructed. We have just verified that this model has the greatest potential for predicting
accurately FEV1 values. We will validate our final model in Section 3. Make note that since no
predictor variables are being dropped, we will not need to conduct a partial F test. However, if
we were to drop a variable for our final model selection, we would want to ensure that it is
sufficient to do so. In order to ensure it is sufficient, we would run a generalized F test on our full

10. 10
model with our reduced model. An example of this has been provided in Appendix A.2 section
2.2.1. Thus, from our model selection process, we finalize that our final model will be:
𝑌6 = .009811𝑋* + .018629𝑋6 + .017802𝑋8 − .026152𝑋: − .843013
The final model was formed using our training data; we proceed with the validation of this model
using the validation data in the Section 3.
3 Model Validation
In order to determine the prediction ability of our final model, we use our validation data. We
use the remaining data from our set to validate the final model to predict FEV1. For the
remaining data, we run the linear regression for the model using all of the predictor variables,
{𝑋*, 𝑋6, 𝑋8, 𝑋:}. Our regression yields the summary output found in Figure 7 for the validation
data.
Figure 7: Summary of Final Model regressed with validation data (right).
Summary of Final Model regressed with model data (left).
When re-estimating the model with the validation data we have 𝑀𝑆𝑃𝑅 = .004169. By
comparing this value to the MSE based on the model-building data we see that the values are
fairly close. In the model-building data regression model, 𝑀𝑆𝐸 = .003847. This is a good
indication that the selected regression model is not seriously biased and gives an appropriate
indication of the the predictive ability of the model. Any R outputs corresponding to Section 3,
model validation, are located in Appendix A.5. The results of both summaries in Figure 7, are
consistent and hence our model seems to validate our validation data with our model data. The
coefficients for the corresponding predictor variables are very similar. This would lead us to
believe that our model is accurately predicting FEV1. Additionally, for our validation model, we
see that we do have a strong correlation; our adjusted R-squared is about 81% for both sets of
data regressed with the chosen model. Thus, our model is a good fit for our data.

11. 11
Figure 8: Final Regression Model on Full Data Set
Now that the data has been validated, we have used the entire data set to estimate the final
regression model. As you can see in Figure 8, the coefficients of each predictor variable are close
to the coefficients for the regression performed on the model and validation data sets. Our final
model is:
𝑌6 = .0101569𝑋* + .0185860𝑋6 + .0127332𝑋8 − .0200069𝑋: − .8442677
4 Discussion
The goal of this analysis was to predict FEV1 values in children of varying age, height, sex, and
indication of being a smoker. We started with 327 children in our data that was set aside strictly
for modeling the regression. We wanted to find a model that would predict FEV1 based off of
this subset of participants from our whole dataset. Keep in mind, the whole data set contained
654 participants.
We began our analysis with training data and created a preliminary model that included four
variables. We tested our residuals for normality and homogeneity. Next, we determined that we
did not have normality or constant error variance. In order to attempt to fix this problem, we
performed several different transformations on our response variable. In both of the
transformations performed, we found that we would get constant error variance but, still have
non-normality. We decided to continue with the model that took the log transformation on the
response variable.
We had expected that there would be multicollinearity issues with our data set by strictly looking
at the correlation scatterplot provided in Appendix A.3. However, when we calculated the VIF
value, no such issues arose. We also tested our preliminary model for outliers by looking at a
variety of influence measures. We were able to conclude that no strong indication of an outlier
existed from these influence measures.
From our model selection process, we found a model that would estimate FEV1. Our final model
actually consisted of all of the four predictor variables. Again, this is not unusual since each of
these predictor variables were significant. Using our final model, that was produced from the
modeling data set, we used our validation data to determine the validity of our model. We found

12. 12
that our final model had a high adjusted R-squared, indicating that our model is an appropriate
fit. Further indication that our model was appropriate came from the comparison of MSPR and
MSE as discussed in Section 3 of this paper.
In order to further improve this model, we should try to account for the normality issues. If we
can appropriately transform the data, we could potentially create a model with a better fit.
Although our initial fit is good, there is room for improvement. We are interested in finding if
there are interaction variables that could produce a better fit for our regression model. An
example of such an interaction variable could consist of looking at X1 times X4 or any other
variation. We could also look at transforming our predictor variables by taking the square, cubic,
etc. of each and do some comparisons of models.
In the end, the analysis of this data has shown us that the FEV1 value for the children in this data
set is dependent on all four predictor variables. In addition, we can draw the conclusion that
FEV1 is affected by age, height, sex, and smoking. Individual correlations between FEV1 and
the predictor variables can be sought; however, the purpose of this analysis was to use multiple
linear regression.
Reflection on Project:
If I were to do another project like this, I would have chosen a data set with more than four
predictor variables. It would have been more interesting to see which variables I would add or
drop if I had 10 or more predictor variables. However, I have learned the process of model
selection from this small subset of predictor variables in the data set I have chosen.

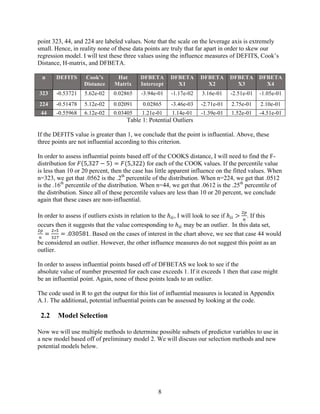
13. 13
Appendix
A Reference for Model Building
A.1 Preliminary Model
Model One: Y1~x1+x2+x3+x4:
s1
Call:
lm(formula = Y1 ~ X1 + X2 + X3 + X4)
Residuals:
Min 1Q Median 3Q Max
-1.31452 -0.22975 0.00576 0.24448 1.49585
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -4.396799 0.310140 -14.177 < 2e-16 ***
X1 0.067625 0.012641 5.350 1.68e-07 ***
X2 0.102853 0.006546 15.713 < 2e-16 ***
X3 0.189609 0.046818 4.050 6.43e-05 ***
X4 -0.113826 0.081545 -1.396 0.164
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.4089 on 322 degrees of freedom
Multiple R-squared: 0.7784, Adjusted R-squared: 0.7756
F-statistic: 282.7 on 4 and 322 DF, p-value: < 2.2e-16
Tests
for
Normality:
𝐻@:Residuals are normally distributed.
𝐻Q:Residuals are not normally
distributed.
Significance level ∝=. 𝟎𝟓
>ks.test(residuals(m1),"pnorm", mean=0,
sd=sd(residuals(m1)))
KS-Test:
One-sample Kolmogorov-Smirnov test
data: residuals(m1)
D = 0.054421, p-value = 0.2875 >.05
alternative hypothesis: two-sided
>shapiro.test(residuals(m1))
Shapiro Test:
Shapiro-Wilk normality test
data: residuals(m1)
W = 0.9889, p-value = 0.01356 <.05
Tests
for
Constant
Error
Variance:
𝐻@:Residuals have constant variance. (accept if 𝑝 − 𝑣𝑎𝑙𝑢𝑒 >. 𝟎𝟓
𝐻Q:Residuals do not have constant variance.
Significance level ∝=. 𝟎𝟓
Brown Forsythe Test:
In order to split my data into two groups, I looked at the age of my participants. Group one contains 155
observations for their Age<=9 and group two contains 172 observations for their Age>=10.
library(car)
data.BF1<- modeldata[order(modeldata[,1]),]
X1.newBF1<-data.BF1[,1]
X2.newBF1<-data.BF1[,3]
X3.newBF1<-data.BF1[,4]
X4.newBF1<-data.BF1[,5]
Y.newBF1<-data.BF1[,2]
z.BF1<-residuals(lm(Y.newBF1~X1.newBF1+X2.newBF1+X3.newBF1+X4.newBF1))
g1<-rep(0,155)
g2<-rep(1,172)
group<-as.factor(c(g1,g2))
leveneTest(z.BF1,group)
Levene's Test for Homogeneity of Variance (center = median)
Df F value Pr(>F)
group 1 20.906 6.867e-06 ***
325
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
BP Test:
library(lmtest)
bptest(Y1~X1+X2+X3+X4,studentize = FALSE)
Breusch-Pagan test
data: Y1 ~ X1 + X2 + X3 + X4
BP = 48.145, df = 4, p-value = 8.803e-10

14. 14
A.2 Transformed Model
2.2.1 Model 2
Generalized F-Test Example:
The F-value is large so this suggests that we would not want want to drop the predictor variable
X4.
Tests
for
Normality:
𝐻@:Residuals are normally distributed.
𝐻Q:Residuals are not normally
distributed.
Significance level ∝=. 𝟎𝟓
Tests
for
Constant
Error
Variance:
𝐻@:Residuals have constant variance. (accept if 𝑝 − 𝑣𝑎𝑙𝑢𝑒 >
. 𝟎𝟓
𝐻Q:Residuals do not have constant variance.
Significance level ∝=. 𝟎𝟓 Outliers

15. 15
2.2.2 Model 3
-3 -2 -1 0 1 2 3
-0.04-0.020.000.020.04
Model 3 Q-Q Plot
Theoretical Quantiles
SampleQuantiles
1.05 1.10 1.15
-0.04-0.020.000.020.04
Model 3
Fitted values
Residuals
Tests
for
Normality:
𝐻@:Residuals are normally distributed.
𝐻Q:Residuals are not normally distributed.
Significance level ∝=. 𝟎𝟓
Tests
for
Constant
Error
Variance:
𝐻@:Residuals have constant variance. (accept if 𝑝 − 𝑣𝑎𝑙𝑢𝑒 >
. 𝟎𝟓
𝐻Q:Residuals do not have constant variance.
Significance level ∝=. 𝟎𝟓

16. 16
A.3 Multicollinearity
V1-Age, V2-FEV, V3-Height, V4-Sex, V5-Smoker
> vif(lm(Y.new1~X1+X2+X3+X4))
X1 X2 X3 X4
2.797353 2.717221 1.071498 1.179844

17. 17
A.4 Model Selection
Forward AIC Backward AIC
Cp
(Intercept)
X1
X2
X3
X4
1400
1300
1300
410
400
360
350
30
30
29
28
13
9.3
7.5
5
adjr2
(Intercept)
X1
X2
X3
X4
0.027
0.054
0.089
0.58
0.58
0.61
0.61
0.8
0.8
0.8
0.8
0.81
0.81
0.81
0.81
Calculations to Compare Models:

18. 18
A.5 Model Validation
Validation Model
Final Model

19. 19
References
[1] Barreiro, T. J., D.O., & Perillo, I., M.D. (2004, March). An Approach to Interpreting
Spirometry. Retrieved February 10, 2016, from http://www.aafp.org/afp/2004/0301/p1107.html
[2] Kavitha, A., Sujatha, C. M., & Ramakrishnan, S. (2010). Prediction of Spirometric Forced
Expiratory Volume (FEV1) Data Using Support Vector Regression. Measurement Science
Review, 10(2). Retrieved February 8, 2016, from
http://www.measurement.sk/2010/S1/Kavitha.pdf
[3] Michael, K. (2005). An Exhalent Problem for Teaching Statistics. Retrieved February 10,
2016, from http://www.amstat.org/publications/jse/v13n2/datasets.kahn.html
Journal of Statistics Education Volume 13, Number 2 (2005),
www.amstat.org/publications/jse/v13n2/datasets.kahn.html
[4] Knudson, RJ, et. al. The Maximal Expiratory Flow-Volume Curve Normal Standards,
Variability, and Effects of Age. Am. Rev. Respir. Dis. 113:589-590, 1976. Retrieved February 8,
2016, from http://cysticfibrosis.com/forums/topic/fev1/
[5] Rosner, B. (1999), Fundamentals of Biostatistics, 5th ed., Pacific Grove, CA: Duxbury.