This document provides an overview of morphology in computational linguistics. It discusses topics like morphemes, inflectional versus derivational morphology, and morphological processes. It also describes how morphology is handled in natural language processing, including the use of finite state automata and transducers to model morphological rules and mappings between surface forms and underlying representations.

1. Morphology
See
Harald Trost “Morphology”. Chapter 2 of R Mitkov (ed.) The
Oxford Handbook of Computational Linguistics, Oxford
(2004): OUP
D Jurafsky & JH Martin: Speech and Language Processing,
Upper Saddle River NJ (2000): Prentice Hall, Chapter 3
[quite technical]

2. 2
Morphology - reminder
• Internal analysis of word forms
• morpheme – allomorphic variation
• Words usually consist of a root plus affix(es),
though some words can have multiple roots, and
some can be single morphemes
• lexeme – abstract notion of group of word forms
that ‘belong’ together
– lexeme ~ root ~ stem ~ base form ~ dictionary
(citation) form

3. 3
Role of morphology
• Commonly made distinction: inflectional vs
derivational
• Inflectional morphology is grammatical
– number, tense, case, gender
• Derivational morphology concerns word
building
– part-of-speech derivation
– words with related meaning

4. 4
Inflectional morphology
• Grammatical in nature
• Does not carry meaning, other than grammatical
meaning
• Highly systematic, though there may be
irregularities and exceptions
– Simplifies lexicon, only exceptions need to be listed
– Unknown words may be guessable
• Language-specific and sometimes idiosyncratic
• (Mostly) helpful in parsing

5. 5
Derivational morphology
• Lexical in nature
• Can carry meaning
• Fairly systematic, and predictable up to a point
– Simplifies description of lexicon: regularly derived
words need not be listed
– Unknown words may be guessable
• But …
– Apparent derivations have specialised meaning
– Some derivations missing
• Languages often have parallel derivations which
may be translatable

6. 6
Morphological processes
• Affixes: prefix, suffix, infix, circumfix
• Vowel change (umlaut, ablaut)
• Gemination, (partial) reduplication
• Root and pattern
• Stress (or tone) change
• Sandhi

7. 7
Morphophonemics
• Morphemes and allomorphs
– eg {plur}: +(e)s, vowel change, yies, fves, um a, , ...
• Morphophonemic variation
– Affixes and stems may have variants which are
conditioned by context
• eg +ing in lifting, swimming, boxing, raining, hoping, hopping
– Rules may be generalisable across morphemes
• eg +(e)s in cats, boxes, tomatoes, matches, dishes, buses
• Applies to both {plur} (nouns) and {3rd sing pres} (verbs)

8. 8
Morphology in NLP
• Analysis vs synthesis
– what does dogs mean? vs what is the plural of dog?
• Analysis
– Need to identify lexeme
• Tokenization
• To access lexical information
– Inflections (etc) carry information that will be needed
by other processes (eg agreement useful in parsing,
inflections can carry meaning (eg tense, number)
– Morphology can be ambiguous
• May need other process to disambiguate (eg German –en)
• Synthesis
– Need to generate appropriate inflections from
underlying representation

9. 9
Morphology in NLP
• String-handling programs can be written
• More general approach
– formalism to write rules which express
correspondence between surface and
underlying form (eg dogs = dog +{plur})
– Computational algorithm (program) which can
apply those rules to actual instances
– Especially of interest if rules (though not
program) is independent of direction: analysis
or synthesis

10. 10
Role of lexicon in morphology
• Rules interact with the lexicon
– Obviously category information
• eg rules that apply to nouns
– Note also morphology-related subcategories
• eg “er” verbs in French, rules for gender agreement
– Other lexical information can impact on morphology
• eg all fish have two forms of the plural (+s and )
• in Slavic languages case inflections differ for inanimate and
animate nouns)

11. 11
Problems with rules
• Exceptions have to be covered
– Including systematic irregularities
– May be a trade-off between treating
something as a small group of irregularities or
as a list of unrelated exceptions (eg French
irregular verbs, English fves)
• Rules must not over/under-generate
– Must cover all and only the correct cases
– May depend on what order the rules are
applied in

12. 12
Tokenization
• The simplest form of analysis is to reduce
different word forms into tokens
• Also called “normalization”
• For example, if you want to count how
many times a given ‘word’ occurs in a text
• Or you want to search for texts containing
certain ‘words’ (e.g. Google)

13. 13
Morphological processing
• Stemming
• String-handling approaches
– Regular expressions
– Mapping onto finite-state automata
• 2-level morphology
– Mapping between surface form and lexical
representation

14. 14
Stemming
• Stemming is the particular case of
tokenization which reduces inflected forms
to a single base form or stem
• (Recall our discussion of stem ~ base form
~ dictionary form ~ citation form)
• Stemming algorithms are basic string-
handling algorithms, which depend on
rules which identify affixes that can be
stripped

15. 15
Finite state automata
• A finite state automaton is a simple and intuitive
formalism with straightforward computational
properties (so easy to implement)
• A bit like a flow chart, but can be used for both
recognition (analysis) and generation
• FSAs have a close relationship with “regular
expressions”, a formalism for expressing strings,
mainly used for searching texts, or stipulating
patterns of strings

16. 16
Finite state automata
• A bit like a flow chart, but can be used for
both recognition and generation
• “Transition network”
• Unique start point
• Series of states linked by transitions
• Transitions represent input to be
accounted for, or output to be generated
• Legal exit-point(s) explicitly identified

17. 17
Example
Jurafsky & Martin, Figure 2.10
• Loop on q3 means that it can account for
infinite length strings
• “Deterministic” because in any state, its
behaviour is fully predictable
q0 q1 q2 q3 q4
b a
a !
a

18. 18
Non-deterministic FSA
Jurafsky & Martin, Figure 2.18
• At state q2 with input “a” there is a choice of
transitions
• We can also have “jump” arcs (or empty
transitions), which also introduce non-
determinism
q0 q1 q2 q3 q4
b a
a !
a
2.19
ε

19. 19
An FSA to handle morphology
q0 q1 q2
q6
q3
f x
o e
c
q5
q4
s
r
q7
y
i
Spot the deliberate mistake: overgeneration

20. 20
Finite State Transducers
• A “transducer” defines a relationship (a
mapping) between two things
• Typically used for “two-level morphology”,
but can be used for other things
• Like an FSA, but each state transition
stipulates a pair of symbols, and thus a
mapping

21. 21
Finite State Transducers
• Three functions:
– Recognizer (verification): takes a pair of strings and
verifies if the FST is able to map them onto each
other
– Generator (synthesis): can generate a legal pair of
strings
– Translator (transduction): given one string, can
generate the corresponding string
• Mapping usually between levels of
representation
– spy+s : spies
– Lexical:intermediate foxNPs : fox^s
– Intermediate:surface fox^s : foxes

22. 22
Some conventions
• Transitions are marked by “:”
• A non-changing transition “x:x” can be
shown simply as “x”
• Wild-cards are shown as “@”
• Empty string shown as “ε”

23. 23
An example
based on Trost p.42
s p y:i +:e s
#:ε #:ε
t o y +:0 s
#:ε #:ε
s h e +:e s
#:ε #:ε
l f:v
w i f:v e s
#:ε #:ε
#spy+s# : spies
#toy+s# : toys

24. 24
Using wild cards and loops
s p y:i +:e s
#:0 #:0
t o y +:0 s
#:0 #:0
@
#:0 y:i +:e
y
+:0
s #:0
Can be collapsed into a single FST:

25. 25
Another example (J&M Fig. 3.9, p.74)
q0
q6
q5
q4
q3
q2
q1
q7
f o x
c a t
d o g
g o o s e
s h e e p
m o u s e
g o:e o:e s e
s h e e p
m o:i u:εs:c e
N:ε
N:ε
N:ε
P:^ s #
S:#
S:#
P:#
lexical:intermediate

26. 26
q0
q1
f o x
c a t
d o g
q0 q1
f s1 s2
s3 s4
s5 s6
c
d
o
a
o
x
t
g

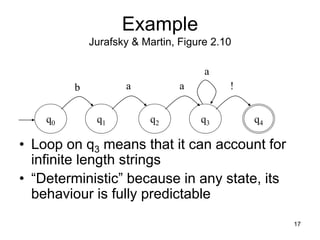
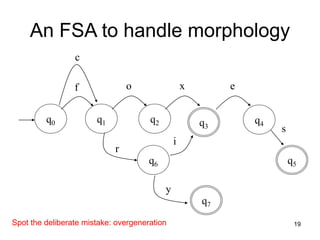
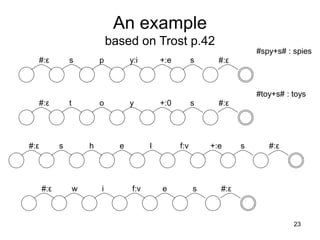
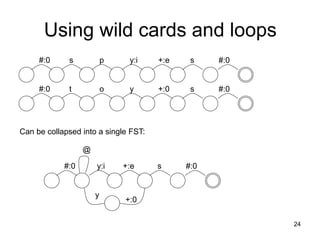
27. 27
q0
q6
q5
q4
q3
q2
q1
q7
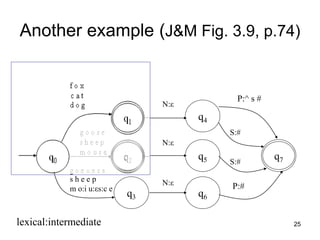
g o o s e
s h e e p
m o u s e
g o:e o:e s e
s h e e p
m o:i u:εs:c e
N:ε
N:ε
N:ε
P:^ s #
S:#
S:#
P:#
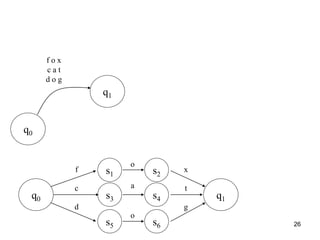
[0] f:f o:o x:x [1] N:ε [4] P:^ s:s #:# [7]
[0] f:f o:o x:x [1] N:ε [4] S:# [7]
[0] c:c a:a t:t [1] N:ε [4] P:^ s:s #:# [7]
[0] s:s h:h e:e p:p [2] N:ε [5] S:# [7]
[0] g:g o:e o:e s:s e:e [3] N:ε [5] P:# [7]
f o x N P s # : f o x ^ s #
f o x N S : f o x #
c a t N P s # : c a t ^ s #
s h e e p N S : s h e e p #
g o o s e N P : g e e s e #
f o x
c a t
d o g

28. 28
Lexical:surface mapping
J&M Fig. 3.14, p.78
ε  e / {x s z} ^ __ s #
f o x N P s # : f o x ^ s #
c a t N P s # : c a t ^ s #
q5
q4
q0 q2 q3
q1
^: ε
#
other
other
z, s, x
z, s, x
#, other z, x
^:ε
s ^:ε
ε:e s
#

29. 29
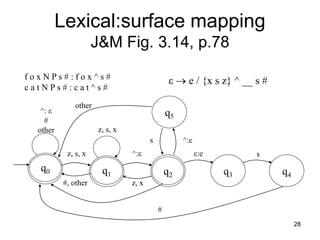
f o x ^ s # f o x e s #
c a t ^ s # : c a t ^ s #
q5
q4
q0 q2 q3
q1
^: ε
#
other
other
z, s, x
z, s, x
#, other z, x
^:ε
s ^:ε
ε:e s
#
[0] f:f [0] o:o [0] x:x [1] ^:ε [2] ε:e [3] s:s [4] #:# [0]
[0] c:c [0] a:a [0] t:t [0] ^:ε [0] s:s [0] #:# [0]

30. 30
FST
• But you don’t have to draw all these FSTs
• They map neatly onto rule formalisms
• What is more, these can be generated
automatically
• Therefore, slightly different formalism

31. 31
FST compiler
http://www.xrce.xerox.com/competencies/content-analysis/fsCompiler/fsinput.html
[d o g N P .x. d o g s ] |
[c a t N P .x. c a t s ] |
[f o x N P .x. f o x e s ] |
[g o o s e N P .x. g e e s e]
s0: c -> s1, d -> s2, f -> s3, g -> s4.
s1: a -> s5.
s2: o -> s6.
s3: o -> s7.
s4: <o:e> -> s8.
s5: t -> s9.
s6: g -> s9.
s7: x -> s10.
s8: <o:e> -> s11.
s9: <N:s> -> s12.
s10: <N:e> -> s13.
s11: s -> s14.
s12: <P:0> -> fs15.
s13: <P:s> -> fs15.
s14: e -> s16.
fs15: (no arcs)
s16: <N:0> -> s12.
s0
s3
s2
s1
s4
c
d
f
g