Gale Pooley, profile picture
Uploaded byGale Pooley
KEY, PPTX744 views

Monopoly

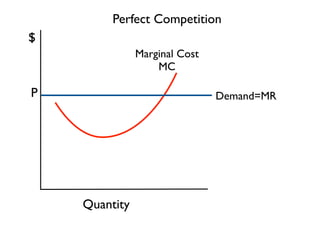
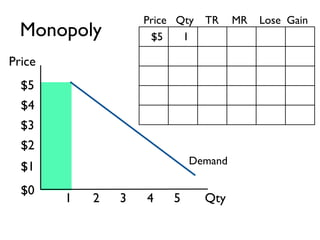
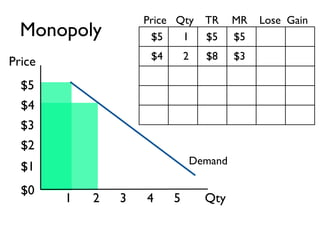
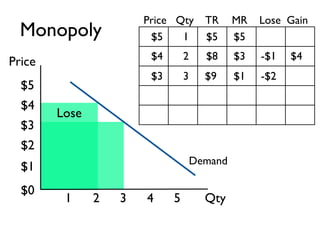
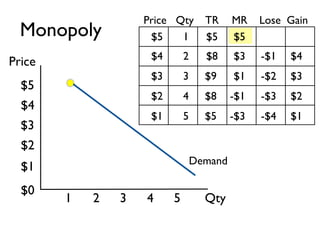
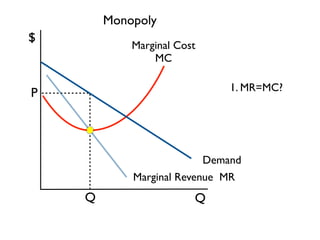
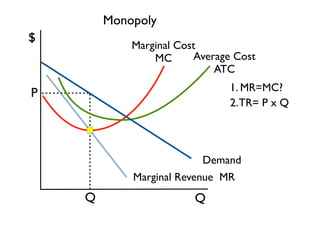
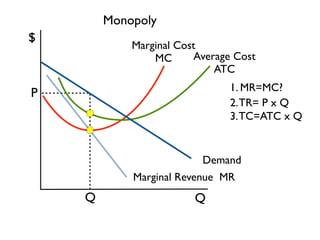
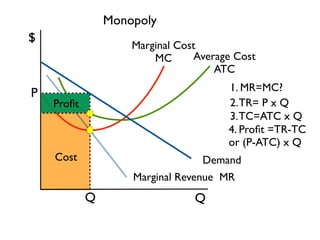
The document discusses the key differences between perfect competition and monopoly market structures. Under perfect competition, there are many small firms producing an identical product, while a monopoly has a single firm producing a unique product with barriers to entry. A monopoly faces a downward-sloping demand curve and must lower prices to increase quantity sold, unlike perfect competition where firms are price takers.

Embed presentation

Download as KEY, PPTX
1 / 116
2 / 116
3 / 116
4 / 116
5 / 116
6 / 116
7 / 116
8 / 116
9 / 116
10 / 116
11 / 116
12 / 116
13 / 116
14 / 116
15 / 116
16 / 116
17 / 116
18 / 116
19 / 116
20 / 116
21 / 116
22 / 116
23 / 116
24 / 116
25 / 116
26 / 116
27 / 116
28 / 116
29 / 116
30 / 116
31 / 116
32 / 116
33 / 116
34 / 116
35 / 116
36 / 116
37 / 116
38 / 116
39 / 116
40 / 116
41 / 116
42 / 116
43 / 116
44 / 116
45 / 116
46 / 116
47 / 116
48 / 116
49 / 116
50 / 116
51 / 116
52 / 116
53 / 116
54 / 116
55 / 116
56 / 116
57 / 116
58 / 116
59 / 116
60 / 116
61 / 116
62 / 116
63 / 116
64 / 116
65 / 116
66 / 116
67 / 116
68 / 116
69 / 116
70 / 116
71 / 116
72 / 116
73 / 116
74 / 116
75 / 116
76 / 116
77 / 116
78 / 116
79 / 116
80 / 116
81 / 116
82 / 116
83 / 116
84 / 116
85 / 116
86 / 116
87 / 116
88 / 116
89 / 116
90 / 116
91 / 116
92 / 116
93 / 116
94 / 116
95 / 116
96 / 116
97 / 116
98 / 116
99 / 116
100 / 116
101 / 116
102 / 116
103 / 116
104 / 116
105 / 116
106 / 116
107 / 116
108 / 116
109 / 116
110 / 116
111 / 116
112 / 116
113 / 116
114 / 116
115 / 116
116 / 116
Microeconomics Monopoly and Anti-Trust Policy
Perfect Monopoly Competition Number of Firms Many One Type of Product Identical Unique Ease of Entry Easy Blocked Demand D = MR D > MR Commodities Utilities Examples Rice Government Apples
Perfect Monopoly Competition Number of Firms Many One Type of Product Identical Unique Ease of Entry Easy Blocked Demand D = MR D > MR Commodities Utilities Examples Rice Government Apples
Perfect Monopoly Competition Number of Firms Many One Type of Product Identical Unique Ease of Entry Easy Blocked Demand D = MR D > MR Commodities Utilities Examples Rice Government Apples
Monopoly
Monopoly Only Seller No Close Substitutes
Barriers to Entry
Barriers to Entry Government Protection Key Resource Network Externalities Economies of Scale
Patents Copyrights
Patents 20 Years Copyrights Lifetime plus 70 Years
Franchise
Franchise Exclusive Legal Provider
New Drugs
New Drugs 10 Years of Testing before Approval 10 Years of Monopoly
Network Externalities
Network Externalities The more who use it The more valuable it becomes
Natural Monopoly
Natural Monopoly One firm can supply entire market at a lower average cost than two or more firms
Natural Monopoly
Natural Monopoly The more I make the lower my costs Large Fixed Costs
Is competition always good?
Is competition always good? Sometimes it can lead to higher prices
Monopoly Output and Price
Monopoly Output and Price Lower Price: Good: Sell More Bad: Less Revenue Per Unit
Perfect Competition
Perfect Competition $ Quantity
Perfect Competition $ P Demand=MR Quantity
Perfect Competition $ Marginal Cost MC P Demand=MR Quantity
Perfect Competition $ Marginal Cost MC P Demand=MR Quantity
Perfect Competition $ Marginal Cost MC P Demand=MR Quantity Q
Perfect Competition $ Marginal Cost MC P Demand=MR Total Revenue Quantity Q
Perfect Competition $ Marginal Cost MC Average Cost ATC P Demand=MR Total Revenue Quantity Q
Perfect Competition $ Marginal Cost MC Average Cost ATC P Demand=MR Total Revenue Quantity Q
Perfect Competition $ Marginal Cost MC Average Cost ATC P Demand=MR Total Cost Quantity Q
Perfect Competition $ Marginal Cost MC Average Cost ATC P Demand=MR Profit Total Cost Quantity Q
Perfect Competition
Perfect Competition Demand
Perfect Competition Demand MR
Perfect Competition Demand = MR
Monopoly Demand MR
Monopoly MR Demand
Monopoly Demand MR
Perfect Competition Monopoly Q D TR MR D TR MR 1 2 3 4 5 Monopoly: To get more Quantity must lower price
Perfect Competition Monopoly Q D TR MR D TR MR 1 2 3 4 5 Monopoly: To get more Quantity must lower price
Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
Perfect Competition Demand
Perfect Competition Demand = MR
Monopoly Demand MR
Price Qty TR MR Lose Gain Monopoly Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 Price $5 Lose $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $5 Lose $4 $3 Gain $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $5 Lose $4 $3 Gain $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $5 Lose $4 $3 Gain $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $5 $4 Lose $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $4 Lose $3 $2 Gain Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $4 $3 Lose $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $3 Lose $2 Demand Gain $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $3 $2 Lose Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Lose Demand $1 Gain $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty Marginal Revenue MR
Monopoly $ Q
Monopoly $ Demand Q
Monopoly $ Demand Marginal Revenue MR Q
Monopoly $ Marginal Cost MC Demand Marginal Revenue MR Q
Monopoly $ Marginal Cost MC 1. MR=MC? Demand Marginal Revenue MR Q
Monopoly $ Marginal Cost MC 1. MR=MC? Demand Marginal Revenue MR Q
Monopoly $ Marginal Cost MC 1. MR=MC? Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC 1. MR=MC? P Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC 1. MR=MC? P 2. TR= P x Q Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q Cost Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P Profit 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P Profit 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost Consumer MC Average Cost Surplus ATC 1. MR=MC? P Profit 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost Consumer MC Average Cost Surplus ATC 1. MR=MC? P Profit 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
Monopoly $ Marginal Cost Consumer MC Average Cost Surplus ATC Deadweight 1. MR=MC? P Loss Profit 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
Antitrust Laws
Antitrust Laws Collusion Felony

More Related Content

PPT
Microeconomics: Introduction and basic concepts
byPie GS
 
PDF
101 lecture 15 monopoly
byGale Pooley
 
KEY
Market structure review
byGale Pooley
 
PPTX
Econ210 Lecture 7 Slides
byguest567ade
 
DOCX
Microeconomics
byvivek Thota
 
PPTX
Monopoly --in microeconomics
byNilormi Das
 
PDF
Hen 368 lecture 9 structure, conduct, performance, and market analysis
byGale Pooley
 
PDF
Micro 15
byGale Pooley
 
Microeconomics: Introduction and basic concepts
byPie GS
 
101 lecture 15 monopoly
byGale Pooley
 
Market structure review
byGale Pooley
 
Econ210 Lecture 7 Slides
byguest567ade
 
Microeconomics
byvivek Thota
 
Monopoly --in microeconomics
byNilormi Das
 
Hen 368 lecture 9 structure, conduct, performance, and market analysis
byGale Pooley
 
Micro 15
byGale Pooley
 

Similar to Monopoly

PDF
101 lecture 15 monopoly
byGale Pooley
 
PDF
101 lecture 17 oligopoly
byGale Pooley
 
PDF
Micro 14
byGale Pooley
 
PPT
Monopoly
byagjohnson
 
PDF
101 lecture 16 monopolistic competition
byGale Pooley
 
PPTX
Graphical analysis
byJanine Bitonio
 
PPT
09 monopoly
byNepDevWiki
 
PPT
Monopoly SFLS online
byianhorner3
 
PPS
Ch 15 micro 1
byabanki
 
PPT
Markets me vi unit
byKanteti Sarvani
 
PPT
Monopoly decisions
byagjohnson
 
PDF
Micro 17.pdf
byGale Pooley
 
PPTX
040813
bypannomion
 
PDF
Perfectcompetition
bydomsr
 
PPTX
Long run for monopoly
byChris Bell
 
PPT
Market structure
byOnline
 
PPT
Lecture 5 27.02.13
byDan Curtis
 
PDF
Micro 18.pdf
byGale Pooley
 
PDF
Chapter 15
bysdugfvna
 
PPTX
Eca iii – the price system perfect competition
bySyed Mohammad Ashiqullah
 
101 lecture 15 monopoly
byGale Pooley
 
101 lecture 17 oligopoly
byGale Pooley
 
Micro 14
byGale Pooley
 
Monopoly
byagjohnson
 
101 lecture 16 monopolistic competition
byGale Pooley
 
Graphical analysis
byJanine Bitonio
 
09 monopoly
byNepDevWiki
 
Monopoly SFLS online
byianhorner3
 
Ch 15 micro 1
byabanki
 
Markets me vi unit
byKanteti Sarvani
 
Monopoly decisions
byagjohnson
 
Micro 17.pdf
byGale Pooley
 
040813
bypannomion
 
Perfectcompetition
bydomsr
 
Long run for monopoly
byChris Bell
 
Market structure
byOnline
 
Lecture 5 27.02.13
byDan Curtis
 
Micro 18.pdf
byGale Pooley
 
Chapter 15
bysdugfvna
 
Eca iii – the price system perfect competition
bySyed Mohammad Ashiqullah
 

More from Gale Pooley

PDF
The Economic History of the United States 15
byGale Pooley
 
PDF
The Economic History of the United States 13
byGale Pooley
 
PDF
The Economic History of the United States 12
byGale Pooley
 
PDF
The Economic History of the United States 11
byGale Pooley
 
PDF
The Economic History of the United States 10
byGale Pooley
 
PDF
The Economic History of the United States 9
byGale Pooley
 
PDF
The Economic History of the United States 8
byGale Pooley
 
PDF
The Economic History of the United States 7
byGale Pooley
 
PDF
The Economic History of the United States 6
byGale Pooley
 
PDF
The Economic History of the United States 5
byGale Pooley
 
PDF
The Economic History of the United States 4
byGale Pooley
 
PDF
The Economic History of the United States 3
byGale Pooley
 
PDF
The Economic History of the United States 2
byGale Pooley
 
PDF
The Economic History of the United States 1
byGale Pooley
 
PDF
The Economic History of the United States 18
byGale Pooley
 
PDF
The Economic History of the United States 17
byGale Pooley
 
PDF
The Economic History of the United States 16
byGale Pooley
 
PDF
The Economic History of the United States 14
byGale Pooley
 
PDF
The Economic History of the United States 13
byGale Pooley
 
PDF
The Economic History of the United States 12
byGale Pooley
 
The Economic History of the United States 15
byGale Pooley
 
The Economic History of the United States 13
byGale Pooley
 
The Economic History of the United States 12
byGale Pooley
 
The Economic History of the United States 11
byGale Pooley
 
The Economic History of the United States 10
byGale Pooley
 
The Economic History of the United States 9
byGale Pooley
 
The Economic History of the United States 8
byGale Pooley
 
The Economic History of the United States 7
byGale Pooley
 
The Economic History of the United States 6
byGale Pooley
 
The Economic History of the United States 5
byGale Pooley
 
The Economic History of the United States 4
byGale Pooley
 
The Economic History of the United States 3
byGale Pooley
 
The Economic History of the United States 2
byGale Pooley
 
The Economic History of the United States 1
byGale Pooley
 
The Economic History of the United States 18
byGale Pooley
 
The Economic History of the United States 17
byGale Pooley
 
The Economic History of the United States 16
byGale Pooley
 
The Economic History of the United States 14
byGale Pooley
 
The Economic History of the United States 13
byGale Pooley
 
The Economic History of the United States 12
byGale Pooley
 

Monopoly

  • 1.
    Microeconomics Monopoly and Anti-Trust Policy
  • 4.
    Perfect Monopoly Competition Number of Firms Many One Type of Product Identical Unique Ease of Entry Easy Blocked Demand D = MR D > MR Commodities Utilities Examples Rice Government Apples
  • 5.
    Perfect Monopoly Competition Number of Firms Many One Type of Product Identical Unique Ease of Entry Easy Blocked Demand D = MR D > MR Commodities Utilities Examples Rice Government Apples
  • 6.
    Perfect Monopoly Competition Number of Firms Many One Type of Product Identical Unique Ease of Entry Easy Blocked Demand D = MR D > MR Commodities Utilities Examples Rice Government Apples
  • 7.
  • 8.
    Monopoly Only Seller No Close Substitutes
  • 9.
  • 10.
    Barriers to Entry GovernmentProtection Key Resource Network Externalities Economies of Scale
  • 11.
  • 12.
    Patents 20 Years Copyrights Lifetime plus 70 Years
  • 13.
  • 14.
  • 15.
  • 16.
    New Drugs 10Years of Testing before Approval 10 Years of Monopoly
  • 17.
  • 18.
    Network Externalities The morewho use it The more valuable it becomes
  • 19.
  • 20.
    Natural Monopoly One firm can supply entire market at a lower average cost than two or more firms
  • 21.
  • 22.
    Natural Monopoly Themore I make the lower my costs Large Fixed Costs
  • 23.
  • 24.
    Is competition always good? Sometimes it can lead to higher prices
  • 25.
  • 26.
    Monopoly Output and Price Lower Price: Good: Sell More Bad: Less Revenue Per Unit
  • 27.
  • 28.
  • 29.
    Perfect Competition $ P Demand=MR Quantity
  • 30.
    Perfect Competition $ Marginal Cost MC P Demand=MR Quantity
  • 31.
    Perfect Competition $ Marginal Cost MC P Demand=MR Quantity
  • 32.
    Perfect Competition $ Marginal Cost MC P Demand=MR Quantity Q
  • 33.
    Perfect Competition $ Marginal Cost MC P Demand=MR Total Revenue Quantity Q
  • 34.
    Perfect Competition $ Marginal Cost MC Average Cost ATC P Demand=MR Total Revenue Quantity Q
  • 35.
    Perfect Competition $ Marginal Cost MC Average Cost ATC P Demand=MR Total Revenue Quantity Q
  • 36.
    Perfect Competition $ Marginal Cost MC Average Cost ATC P Demand=MR Total Cost Quantity Q
  • 37.
    Perfect Competition $ Marginal Cost MC Average Cost ATC P Demand=MR Profit Total Cost Quantity Q
  • 38.
  • 39.
  • 40.
  • 41.
  • 42.
    Monopoly Demand MR
  • 43.
    Monopoly MR Demand
  • 44.
    Monopoly Demand MR
  • 45.
    Perfect Competition Monopoly Q D TR MR D TR MR 1 2 3 4 5 Monopoly: To get more Quantity must lower price
  • 46.
    Perfect Competition Monopoly Q D TR MR D TR MR 1 2 3 4 5 Monopoly: To get more Quantity must lower price
  • 47.
    Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
  • 48.
    Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
  • 49.
    Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
  • 50.
    Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
  • 51.
    Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
  • 52.
    Perfect Competition Monopoly Q D TR MR D TR MR 1 $3 $3 $3 $5 $5 $5 2 $3 $6 $3 $4 $8 $3 3 $3 $9 $3 $3 $9 $1 4 $3 $12 $3 $2 $8 -$1 5 $3 $15 $3 $1 $5 -$3 Monopoly: To get more Quantity must lower price
  • 53.
  • 54.
  • 55.
    Monopoly Demand MR
  • 56.
    Price Qty TR MR Lose Gain Monopoly Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 57.
    Price Qty TR MR Lose Gain Monopoly $5 1 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 58.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 59.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 60.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 61.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 62.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 63.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 64.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 65.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 Price $5 Lose $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 66.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $5 Lose $4 $3 Gain $2 Demand $1 $0 1 2 3 4 5 Qty
  • 67.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $5 Lose $4 $3 Gain $2 Demand $1 $0 1 2 3 4 5 Qty
  • 68.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $5 Lose $4 $3 Gain $2 Demand $1 $0 1 2 3 4 5 Qty
  • 69.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 70.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 71.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 72.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 73.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $5 $4 Lose $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 74.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $4 Lose $3 $2 Gain Demand $1 $0 1 2 3 4 5 Qty
  • 75.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 76.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 77.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 78.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 79.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $4 $3 Lose $2 Demand $1 $0 1 2 3 4 5 Qty
  • 80.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $3 Lose $2 Demand Gain $1 $0 1 2 3 4 5 Qty
  • 81.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 82.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 83.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 84.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 85.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $3 $2 Lose Demand $1 $0 1 2 3 4 5 Qty
  • 86.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Lose Demand $1 Gain $0 1 2 3 4 5 Qty
  • 87.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 88.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 89.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 90.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 91.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty
  • 92.
    Price Qty TR MR Lose Gain Monopoly $5 1 $5 $5 $4 2 $8 $3 -$1 $4 Price $3 3 $9 $1 -$2 $3 $5 $2 4 $8 -$1 -$3 $2 $4 $1 5 $5 -$3 -$4 $1 $3 $2 Demand $1 $0 1 2 3 4 5 Qty Marginal Revenue MR
  • 93.
  • 94.
    Monopoly $ Demand Q
  • 95.
    Monopoly $ Demand Marginal Revenue MR Q
  • 96.
    Monopoly $ Marginal Cost MC Demand Marginal Revenue MR Q
  • 97.
    Monopoly $ Marginal Cost MC 1. MR=MC? Demand Marginal Revenue MR Q
  • 98.
    Monopoly $ Marginal Cost MC 1. MR=MC? Demand Marginal Revenue MR Q
  • 99.
    Monopoly $ Marginal Cost MC 1. MR=MC? Demand Marginal Revenue MR Q Q
  • 100.
    Monopoly $ Marginal Cost MC 1. MR=MC? P Demand Marginal Revenue MR Q Q
  • 101.
    Monopoly $ Marginal Cost MC 1. MR=MC? P 2. TR= P x Q Demand Marginal Revenue MR Q Q
  • 102.
    Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q Demand Marginal Revenue MR Q Q
  • 103.
    Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q Demand Marginal Revenue MR Q Q
  • 104.
    Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q Demand Marginal Revenue MR Q Q
  • 105.
    Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q Demand Marginal Revenue MR Q Q
  • 106.
    Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q Demand Marginal Revenue MR Q Q
  • 107.
    Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q Cost Demand Marginal Revenue MR Q Q
  • 108.
    Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
  • 109.
    Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
  • 110.
    Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P Profit 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
  • 111.
    Monopoly $ Marginal Cost MC Average Cost ATC 1. MR=MC? P Profit 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
  • 112.
    Monopoly $ Marginal Cost Consumer MC Average Cost Surplus ATC 1. MR=MC? P Profit 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
  • 113.
    Monopoly $ Marginal Cost Consumer MC Average Cost Surplus ATC 1. MR=MC? P Profit 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
  • 114.
    Monopoly $ Marginal Cost Consumer MC Average Cost Surplus ATC Deadweight 1. MR=MC? P Loss Profit 2. TR= P x Q 3. TC=ATC x Q 4. Profit =TR-TC or (P-ATC) x Q Cost Demand Marginal Revenue MR Q Q
  • 115.
  • 116.

Editor's Notes

  • #2 \n
  • #3 \n
  • #4 \n
  • #5 \n
  • #6 \n
  • #7 \n
  • #8 \n
  • #9 \n
  • #10 \n
  • #11 \n
  • #12 \n
  • #13 \n
  • #14 \n
  • #15 \n
  • #16 \n
  • #17 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #18 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #19 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #20 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #21 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #22 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #23 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #24 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #25 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #26 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #27 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #28 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #29 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #30 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #31 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #32 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #33 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #34 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #35 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #36 Perfect Competition\n\nIn this video we’re going to talk about Perfect Competition.\n\nFirst we’ll draw and label our price-quantity graph.\n\nThen we’ll draw the demand curve.\n\nRemember that under perfect competition there is one price level for all individual sellers. This means the demand curve is flat. This also means the marginal revenue curve is the same as the demand curve. So price and demand and marginal revenue are all on the same line.\n\nSo the first question we want to answer is “At what level should we produce to maximize profits?” We always answer this question with the equation MR=MC.\nSo we need to see a marginal cost curve. This curve is a “U-shape” to indicate that costs typically tend to decline and then increase. \n\nNow that we have a MR and a MC curve we can pin-point the intersection. \n\nThe next step is to draw a vertical line down to the Quantity axis. This line will point to the quantity we should produce to maximize profits. \n\nWe can then calculate Total Revenue. This is P times Q, or this area.\n\nThe next step is to calculate Total Costs. Total Costs are calculated as ATC x Q. We need the ATC curve to do this. Once we know the ATC then we pin-point the intersection of the ATC curve and the vertical line we drew. Then we daw a horizontal line from this point over to the price axis. The area below this line represents our total costs. \n\nNow we can calculate profits. The equation is TR -TC, or another way is (Price-ATC) x Q. \n\nLet’s quickly review. We start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. We then look at the Average Total Cost curve and pinpoint where it crosses our line and then draw a horizontal line. The area below this line is Total Cost and the area above is profit. \n\nLets look at another example.\n\nWe start with a flat demand curve which is also our marginal revenue curve. We then add a marginal cost curve. Using MR=MR we pinpoint the profit maximizing location and draw a line down to quantity. This are is total revenue. In this case the ATC curve is above the price line. If this is the case we will be looking for the location that minimizes losses. We pinpoint where ATC crosses our line and then draw a horizontal line. The area is Total Cost. Since Total Costs are larger than Total Revenue, this area represents our losses. Remember that using MC=MR we can figure out where our losses are minimized. \n\nAlright, now you know how to analyze Perfect Competition. \n\nDon’t forget you can rewind this video to make sure you understand how the graph works.\n
  • #37 \n
  • #38 \n
  • #39 \n
  • #40 \n
  • #41 \n
  • #42 \n
  • #43 \n
  • #44 \n
  • #45 \n
  • #46 \n
  • #47 \n
  • #48 \n
  • #49 \n
  • #50 \n
  • #51 \n
  • #52 \n
  • #53 \n
  • #54 \n
  • #55 \n
  • #56 \n
  • #57 \n
  • #58 \n
  • #59 \n
  • #60 \n
  • #61 \n
  • #62 \n
  • #63 \n
  • #64 \n
  • #65 \n
  • #66 \n
  • #67 \n
  • #68 \n
  • #69 \n
  • #70 \n
  • #71 \n
  • #72 \n
  • #73 \n
  • #74 \n
  • #75 \n
  • #76 \n
  • #77 \n
  • #78 \n
  • #79 \n
  • #80 \n
  • #81 \n
  • #82 \n
  • #83 \n
  • #84 \n
  • #85 \n
  • #86 \n
  • #87 \n
  • #88 \n
  • #89 \n
  • #90 \n
  • #91 \n
  • #92 \n
  • #93 \n
  • #94 \n
  • #95 \n
  • #96 \n
  • #97 \n
  • #98 \n
  • #99 \n
  • #100 \n
  • #101 \n
  • #102 \n
  • #103 \n
  • #104 \n
  • #105 \n
  • #106 \n
  • #107 \n
  • #108 \n
  • #109 \n
  • #110 \n
  • #111 \n
  • #112 \n
  • #113 \n
  • #114 \n
  • #115 \n
  • #116 \n
  • #117 \n
  • #118 \n
  • #119 \n
  • #120 \n
  • #121 \n
  • #122 \n
  • #123 \n
  • #124 \n
  • #125 \n
  • #126 \n
  • #127 \n
  • #128 \n
  • #129 \n
  • #130 \n
  • #131 \n
  • #132 \n
  • #133 \n
  • #134 \n
  • #135 \n
  • #136 \n
  • #137 \n
  • #138 \n
  • #139 \n
  • #140 \n
  • #141 \n
  • #142 \n
  • #143 \n
  • #144 \n
  • #145 \n
  • #146 \n
  • #147 \n
  • #148 \n
  • #149 \n
  • #150 \n
  • #151 \n
  • #152 \n
  • #153 \n
  • #154 \n
  • #155 \n
  • #156 \n
  • #157 \n
  • #158 \n
  • #159 \n
  • #160 \n
  • #161 \n
  • #162 \n
  • #163 \n
  • #164 \n
  • #165 \n
  • #166 \n