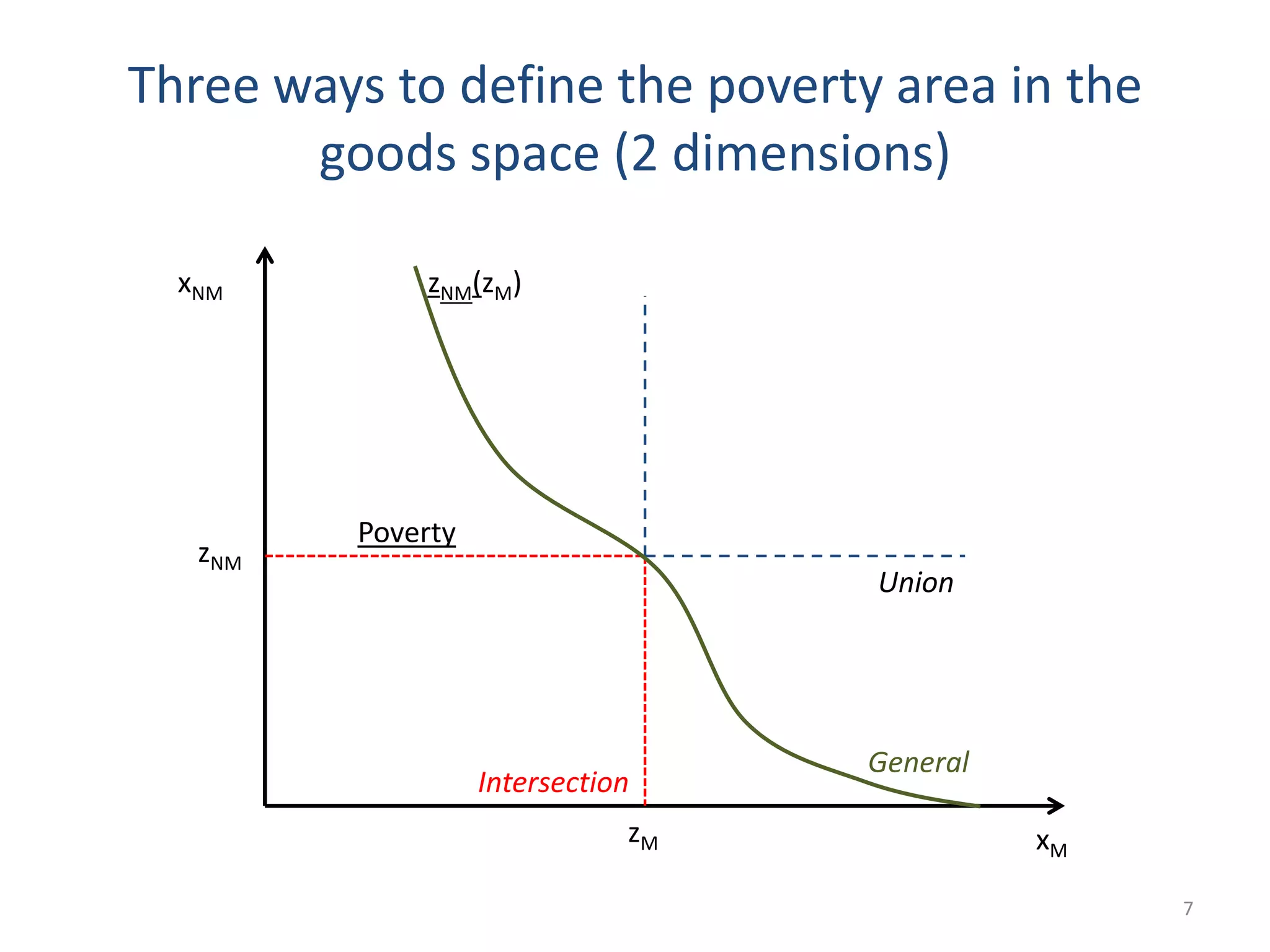
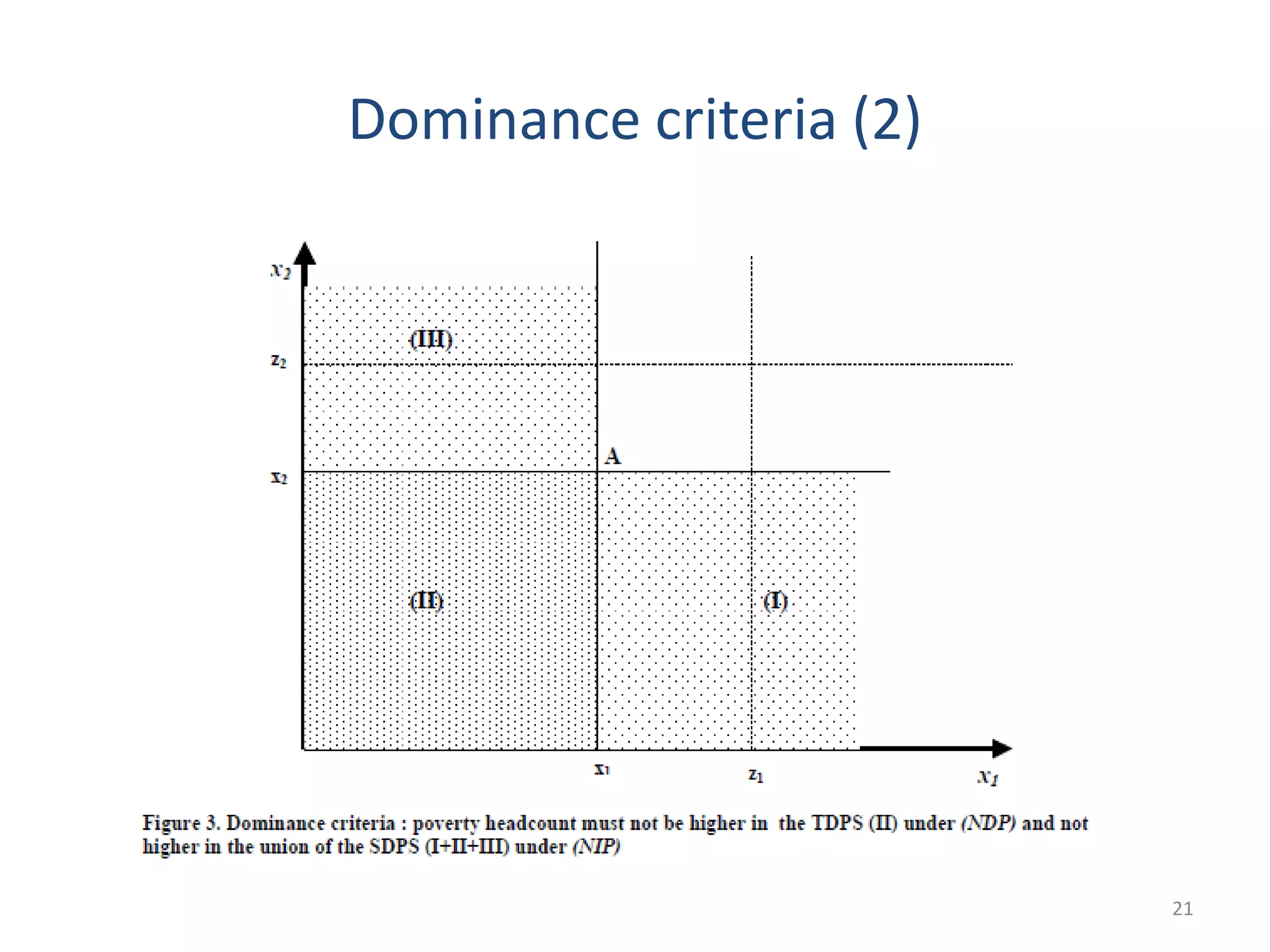
The document discusses multi-dimensional poverty measurement, highlighting the complexities and various approaches, including the capability approach, statistical methods, and the counting approach. It evaluates existing measures, questions the effectiveness of aggregating dimensions into single indicators, and emphasizes the importance of understanding different dimensions of poverty. The conclusion reflects ongoing debates and the necessity for appropriate frameworks and measures in understanding poverty.

1. Multi-Dimensional Poverty
Measurement: where do we stand?
François Bourguignon
Paris School of Economics
Monash University, May 2013
1
Centre for Development Economics
presents

2. Multi-Dimensional Poverty
Measurement: where do we stand?
François Bourguignon
Paris School of Economics
Monash University, May 2013
2
Centre for Development Economics
presents

3. State of play
• Sen's impulse through the capability approach and the HDI
• Income imperfectly correlated with other dimensions of well-
being
• "Poverty is multi-faceted"
– How to measure it? Does it make sense to aggregate all its
dimensions into a single indicator? Isn't income poverty
sufficient?
– Does measurement yield information on how to reduce it?
• This presentation as a contribution to the debate
3

4. State of play (2)
The various approaches to measurement
• Purely statistical approaches (fuzzy sets, entropy, distance,..)
• Extension of normative poverty measures to two (or more)
dimensions (Tsui, 2002, Bourguignon-
Chakravarty, 2003, 2007, Duclos et al., 2006, ...)
• Counting approach and 'dual cut-off' presented as an alternative
(Alkire-Foster, 2011)
Practically:
• Increasing use of the dual cut-off approach, much less of the
normatively grounded measures
• At the same time, strong criticisms of the counting approach and of
the goal of summarizing multi-dimensional poverty into one single
number (Ravallion, 2011)
• Where do we stand as of now? Where should we go?
4

5. Outline
1. What kind of poverty do we want to measure?
2. A basic analytical framework
3. "Adding-up" dimensions: back to unidimensional
measures
4. Generalizing FGT and dominance criteria
5. Counting approach and the AF measure
6. Conclusion
5

6. 1) What kind of poverty do we want to
measure?
1) Individual welfare
• Utility depends on: a) Market goods; b) Non-market goods (health
status, environment, security, ..)
• Poverty = inability to consume a minimum basket
• Market goods: monetary expenditure threshold (standard 'income'
poverty, price aggregation)
• Non-market goods: no price available, a minimum has to be
specified for each one of them …
• … or a locus in the space of goods (Duclos et al.)
• To what extent does non-market good consumption depend also
on income? (Imperfect correlation = preference heterogeneity ?)
6

7. Three ways to define the poverty area in the
goods space (2 dimensions)
7
xM
zM
xNM
zNM
Poverty
zNM(zM)
Union
Intersection
General

8. What do we want to measure? (cont'd)
2) The capability approach
• Set of possible functionings defined by:
assets, education, health, access to markets, justice, …
• Poverty defined by low levels of these capability determinants
• No price available to aggregate (except for wealth): minimum
endowment in each dimension or minimum of some
combination of them
3) Implications of the capability/well being distinction: make sure
that the framework underpinning the choice of multiple
dimensions is consistent.
– Money income and housing quality or money income and education
are inconsistent (except across countries for the latter).
8

9. 2. Basic analytical framework: sequential
aggregation
• N individuals (i), J dimensions (j), "attributes" of i : xi.= (xij)
• Relative shortfall or deprivation in dimension j:
where zj = poverty line in dimension j
• Aggregate shortfall, or poverty intensity, for individual i:
• Aggregating across individuals, a poverty measure in the
sense of π is simply:
9
)/1,0( jijij zxMaxy
0)0(;0)(:)( .. iji yy
N
i
iy
N
P
1
. )(
1

10. Basic analytical framework (2)
A simple decomposition
• Poverty headcount in the sense of π:
• Average intensity of poverty among the poor:
• Therefore:
10
N
i
iyI
N
H
1
. 0)(
1
0)(
.
.
)(
1
iy
iy
H
P
PHP

11. Basic analytical framework (3)
Remarks:
• Order of aggregation steps:
– One might aggregate first the shorfalls across individuals and then
across dimensions: yet, this would be missing the joint distribution of
the various dimensions
• Comparing two distributions (yA and yB )
– Pπ comparison:
– Dominance criterion: e.g. A dominates B in the sense of Π.
11
withinallforBPAP ())()(
)(/)( BPAP

12. 3. "Adding-up" dimensions: back to
unidimensional measures
Case where the function π is linear:
Then:
However:
Instead, Hπ is the proportion of people with at least one deprivation
(Union)
Multidimensional poverty thus appears as some linear combination
of unidimensional poverty measures
Roughly speaking: there is more poverty in A than in B if
unidimensional poverty is on average higher in A than in B
12
0,)(
1
. jij
J
j
ji byby
j
J
j
j PGbP .
1
j)dimensionin(headcount
1
J
j
z
j
j
HH

13. "Adding-up" dimensions (2)
The additive separability case:
Then:
The overall poverty index is a combination of unidimensional
poverty indices defined on the poverty intensity functions fj.
Example:
13
0(),0)0(,0,)()( '
1
. jjjijj
J
j
ji ffbyfby
j
f
J
j
j j
PbP .
1
0)( j
jj
ijijj forPPyyf
jjf
j

14. "Adding-up" dimensions (3)
Weight-dominance in the separability case:
Equivalent to:
In the additive separability case, there is less multi-
dimensional poverty in A than in B for all possible weights iff
poverty is smaller in A than in B for each dimension.
14
jallforbBPbBPAPbAP j
j
f
J
j
j
j
f
J
j
j jj
0)(.)()(.)(
11
jBPAP j
f
j
f jj
)()(

15. "Adding-up" dimensions (4)
Overall dominance in the additive separability case:
Equivalent to:
Overall (first-order) dominance of A over B requires (first-order)
unidimensional poverty dominance in all dimensions.
The same result applies for second-order dominance
IN SUMMARY: The additive separability of π makes multidimensional
poverty analysis equivalent to unidimensional poverty analysis in
each dimension.
The cross distribution of attributes does not matter!!
15
jfffbBPbBPAPbAP jjjjf
J
j
jf
J
j
j jj
0();0)0(:,0)()()()( '
11
jzvBHAH j
vv
jj
,)()( 11

16. "Adding-up" dimensions (5)
• Effect of a monotonically increasing transformation of an additively
separable individual poverty intensity function
It is now the case that:
• Taking a linear approximation leads to:
The joint distribution of the J attributes now matters
16
0()',0,0,)(
1
. jj
J
j
ji byby j
ij
jk
ijik
J
j i k
kjj yyb
N
bP )('
1
1
j
J
j
j j
PbP .
1

17. 4. Generalizing FGT and dominance criteria
• In the case J=2, an interesting particular specification is:
which generalizes the familiar FGT or Pα measure: the α-
power of the β-power mean of the two shortfalls
(Bourguignon and Chakravarty).
• β determines the substitutability between the shortfalls of the
two attributes in defining the overall poverty intensity; α
measures the aversion to poverty; b the relative weight of the
two attributes.
17
1,0;0,)1(
1
2
,,
1
bybby
N
P
i
i
b
i

18. Generalizing FGT (2)
• In the case where the second attribute is discrete (0/1) with
z2=1 this measure becomes:
where nk is the proportion of the population with yi2 = k (=0/1).
Multidimensional poverty is a weigthed average of attribute 1's
Pα for the non-poor in attribute 2 and a 'modified Pα' for the
others.
The 'modified Pα' increases the poverty intensity for any
shortfall yi1 but at the declining rate with yi1.
18
11
1
2
10
2
11
1
1
1
0
i
ii
y
i
b
b
yy
nN
n
yP
N
n

19. Generalizing FGT (3)
• In the case where the two attributes are discrete (0/1) with
z2=1 the generalized FGT becomes:
where nkm is the number of individuals with yi1 = k (=0/1) and
yi2 = m (=0/1) .
19
/
01
/
1011 )1(.
1
bnbnn
N

20. Dominance criteria (1)
• (Bourguignon-Chakravarty, 2007, in the case J=2)
Let:
Theorem 1 (Union): Pπ(A) ≤ Pπ(B) for all π( ) in Π+ iff:
where is the two-dimensioned headcount
Theorem 2 (Intersection): Pπ(A) ≤ Pπ(B) for all π( ) in Π- iff:
20
0;0,:(.,.)
0;0,:(.,.)
2121
2121
yyyy
yyyy
2,1)()()()()()( 21212121
12211221 jzvBHBHBHAHAHAH jj
vvvvvvvv
21
12
vv
H
2,1)()(;2,1),()( 2121
1212 jzvBHAHjBHAH jj
vvvvv
j
v
j
jj

21. Dominance criteria (2)
21

22. Generalized FGT and dominance criteria (end)
• Π+ and Π- in the case of generalized FGT (Pα,β,b)
• Interestingly enough, this condition does not depend only on
the substitutability parameter β but also on the poverty
aversion parameter α.
• Other dominance result (Duclos et al., 2006), idem theorem 2
(intersection) for general shape of the poverty domain.
• Difficulty of using generalized FGT for J>2. Should the
susbtitutability be the same for all dimensions? Possibly of
using nested CES functions.
22
1/)1(() 21
iffybby ii

23. 5. Counting approach and the AF measure
• One of the first approaches used in poverty measurement:
counting the number of deprivation
• Recently formalized by Alkire and Foster (2011) as 'dual
cutoff':
– First cutoff : poverty threshold in each dimension
– Second cutoff: poor = individuals deprived in k dimensions or more
(out of J)
• Interestingly enough, the AF measure can be obtained as a
non-linear transformation of the generalized FGT (along the
lines of Atkinson, 2003)
23

24. Counting approach (2)
• Basic property:
• Counting the number of deprivations among J:
• Dual cutoff: poor if at least k deprivations
• Headcount:
24
0)()1(0)(01,0 0 yiffyLimthenandyIf
0)(
1
.. kycI
N
H i
i
J
j
iji yyc
1
0. lim)(

25. Counting approach (3)
• Simple poverty intensity = average proportion of deprivations
• And, after introducing weights, for the various dimensions
• Poverty intensity = non-linear monotonic transformation of
additively separable function of shortfalls
• Poverty intensity = non-linear monotonic transform of poverty
intensity in Generalized FGT (α = β)
25
i
iiii ij
yLimycwithkycIyc
J
y )()().(
1
)( ....0
i
jiii
j
j
ib ij
ybLimycwithkycIyc
b
y )()().(
1
)( ....

26. Counting approach (4)
• Full dual cutoff AF measure:
• Generalized AF measure:
But properties are different because poverty intensity is not
anymore a monotonic transform of a (single) additively separable
function of shortfalls.
• Because of this, and because of non-differentiability and
discontinuities, differences are expected in comparison with
generalized FGT (Datt, 2013)
26
i
jiii
i
j
j
b ij
ybLimycwithkycIyc
bN
AF 0... )()().(
1
i
jiiij
i j
ijj
j
j
G ij
ybLimycwithkycIyLimyb
bN
AF 0..0 )()(.
1

27. Conclusion
General points
• Many indicators available to describe the average distance in
between an observation and a reference frontier (or point)
called 'poverty' in a multidimensional space
• Preference for those with an economic/normative
interpretation and generalizing known uni-dimensional
concepts
• Experience with application of available measures is key. Too
early to make judgements
• Overall context matters: what it is that we try to measure (e.g.
space of outcomes/capability)
27

28. Conclusion(2)
More specific points
• Common structure between straight generalizations of one-
dimensional measure, FGT type, and 'counting approach' (AF)
• Yet, properties likely to differ because more or less non-
linearity in transformation of a basic poverty-intensity (or
distance) function
• Nice decomposability properties in case of additive separable
function but covariance/copula not in the picture
• Decomposability properties lack transparency in other
cases, except with dominance criteria
• Policy application requires such decomposability w.r.t.
marginal distributions and copula
28

29. Conclusion(3)
Work is still ongoing…
After all, it took us a fair amount of time to master one-
dimensional poverty measurement!
29

30. 30