The Digital Signature Standard (DSS) was designed by NIST and NSA in the early 1990s to be a US government approved digital signature scheme. It uses the Digital Signature Algorithm (DSA) which creates 320-bit signatures with 512-1024 bit security, making it smaller and faster than RSA. DSA is based on the discrete logarithm problem and uses public and private keys to generate signatures for verification in a similar way to the ElGamal and Schnorr signature schemes.

1. Digital Signature Standard (DSS)
 US Govt approved signature scheme
 Designed by NIST & NSA in early 90's
 Published as FIPS-186 in 1991
 Revised in 1993, 1996 & then 2000
 Uses the SHA hash algorithm
 DSS uses a Digital Signature Algorithm (DSA) based
on the ElGamal scheme with some ideas from the
Schnorr scheme
VIT/SCOPE/BCSE-309L/CNS/MODULE 5 1

2. DSS vs RSA Signatures
VIT/SCOPE/BCSE-309L/CNS/MODULE 5 2

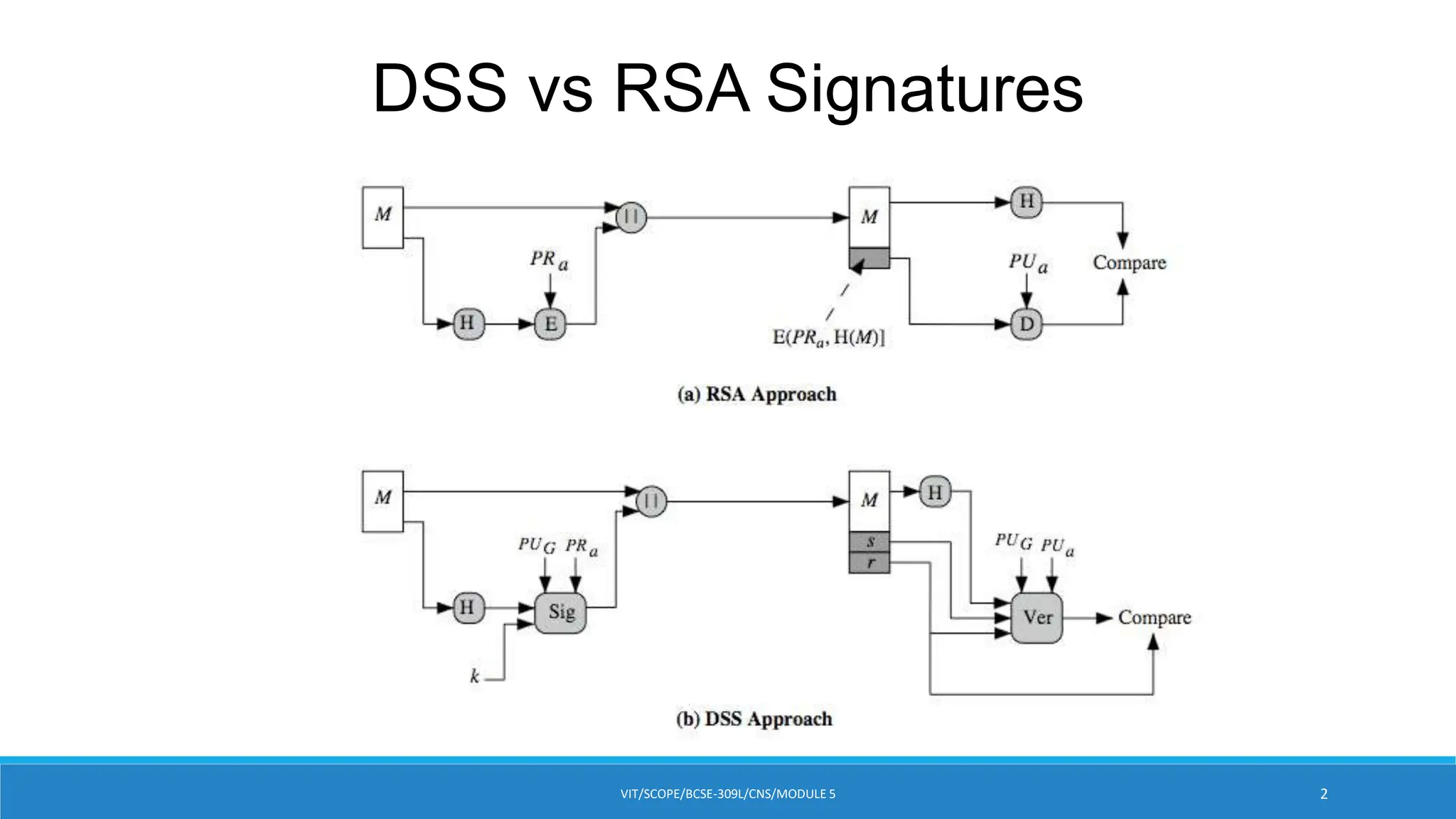
3. © 2020 PEARSON EDUCATION, INC., HOBOKEN, NJ. ALL RIGHTS RESERVED.
Figure 13.2 Two Approaches to Digital Signatures
M
H
| |
PR a
(a) RSA Approach
M
E(PRa, H(M)]
E D
H
Compare
PUa
M
H
| |
PR a
PUG
M
Sig Ver
H
Compare
k
s
r
PUa
PUG
(b) DSA Approach

4. Digital Signature Algorithm (DSA)
 Creates a 320 bit signature with 512-1024 bit security
 Smaller and faster than RSA
 DSA is digital signature only unlike RSA which is a public-
key technique
 Security depends on difficulty of computing discrete
logarithms
 Variant of ElGamal & Schnorr schemes
VIT/SCOPE/BCSE-309L/CNS/MODULE 5 4

5. DSA Key Generation
 Global public key values: p,q,g
 Choose 160-bit prime number q
 Choose a large prime p with 2L-1 < p < 2L
• where L= 512 to 1024 bits and is a multiple of 64
• such that q is a 160 bit prime divisor of (p-1)
 Choose g = h(p-1)/q where 1<h<p-1 and h(p-1)/q mod p > 1
 Users choose private key & compute public key:
 Choose random private key: x<q
 Compute public key: y = gx mod p
VIT/SCOPE/BCSE-309L/CNS/MODULE 5 5

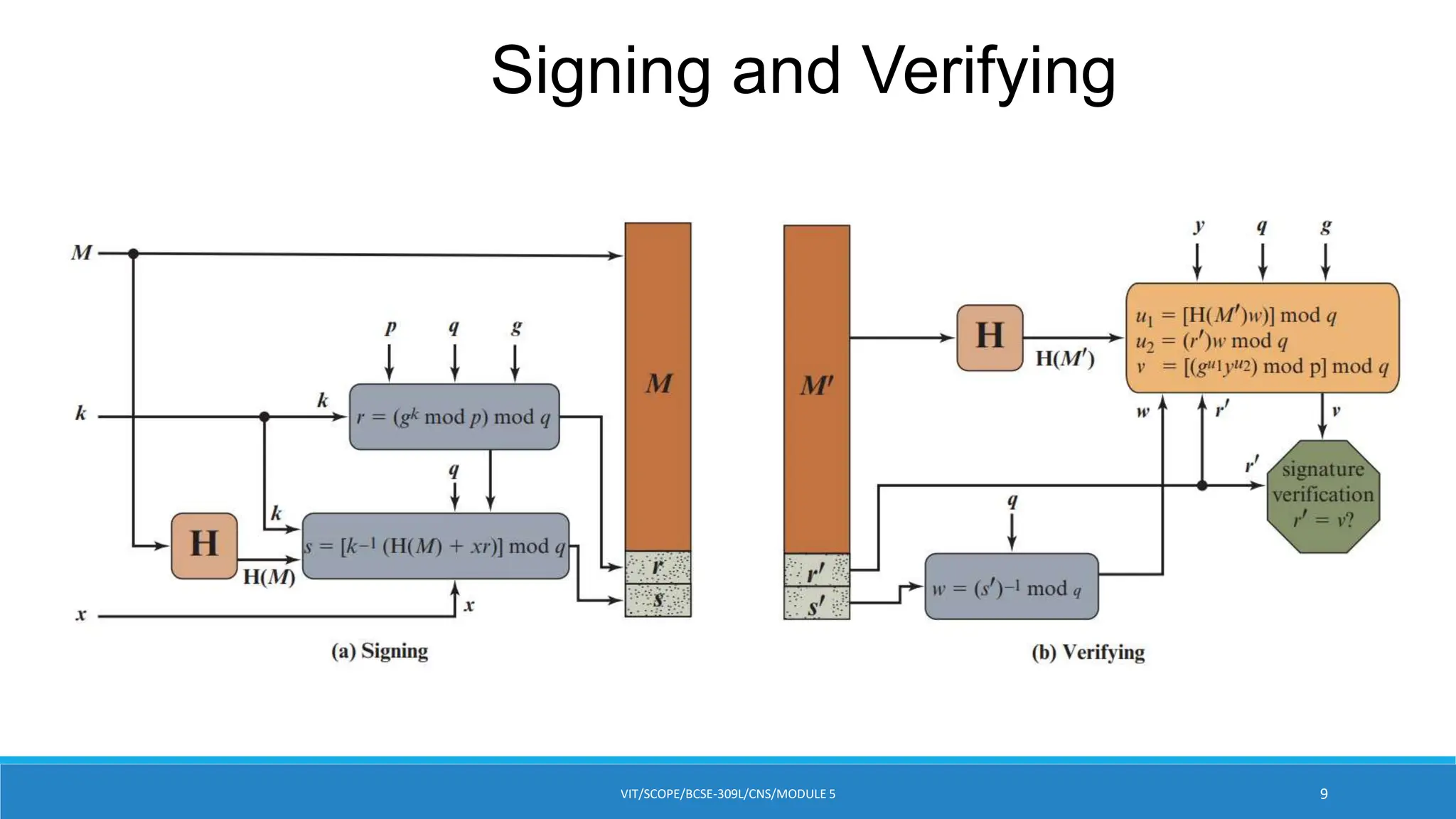
6. DSA Signature Creation
 To sign a message M the sender:
 Generates a random signature key k, k<q
o k must be random, be destroyed after use, and never be reused.
 Then computes signature pair:
r = (gk mod p)mod q
s = [k-1(H(M)+ xr)] mod q
 Sends signature (r,s) with message M
VIT/SCOPE/BCSE-309L/CNS/MODULE 5 6

7. DSA Signature Verification
 Having received M & signature (r,s)
 To verify a signature, recipient computes:
◦ w = s-1 mod q
◦ u1= [H(M)w ]mod q
◦ u2= (rw)mod q
◦ v = [(gu1 yu2)mod p ]mod q
 If v=r then signature is verified
VIT/SCOPE/BCSE-309L/CNS/MODULE 5 7

8. © 2020 PEARSON EDUCATION, INC., HOBOKEN, NJ. ALL RIGHTS RESERVED.

9. DSA Signing and Verifying
VIT/SCOPE/BCSE-309L/CNS/MODULE 5 9