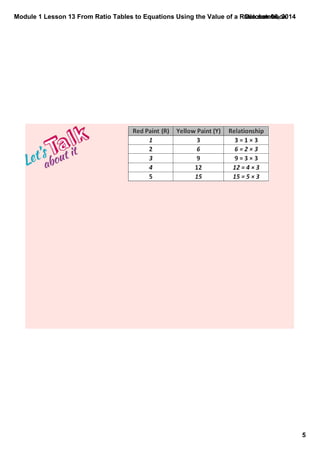
This document provides lesson materials for a math class on ratios and using ratio tables to write equations. It includes examples of setting up ratio tables and writing equations to model relationships based on given ratios. Students are asked to complete similar practice problems for homework involving setting up ratio tables and writing equations for scenarios about mixing paint, military exercises, observing cars on a road trip, and a running training program. The value of the ratio is discussed as appearing in both the ratio table and the corresponding equation relating the variables.

1. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
1
October 06, 2014
Monday Exit Ticket Lesson 13
Tuesday Problem Set Lesson 13
Wednesday Problem Set Lesson 14
Thursday Problem Set Lesson 15
Friday
Half Day of School (dismiss 4th period)
Complete Review Packet
Mid­Module
Assessment
Wednesday

2. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
2
October 06, 2014
Module 1
Ratios and Unit Rates
Topic B: Collections of Equivalent Ratios
Lesson 13: From Ratio Tables
to Equations Using the Value of a Ratio

3. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
3
October 06, 2014
Exercise 1
Jorge is mixing a special shade of orange paint.
He mixed 1 gallon of red paint with 3 gallons of yellow paint.
Based on this ratio, which of the following statements are true?
of a 4­gallon
mix would be yellow paint.
34
13
Every 1 gallon of yellow paint requires gallon of red paint.
TRUE
Every 1 gallon of red paint requires 3 gallons of yellow paint.
There is 1 gallon of red paint in a 4­gallon
mix of orange paint.
TRUE
TRUE
There are 2 gallons of yellow paint in an 8­gallon
mix of orange paint.
FALSE
= four gallon
= four gallon mix TRUE
= four gallon mix
= eight gallon mix

4. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
4
October 06, 2014
Exercise 2
Based on the information on red and yellow paint given
in the warm up, complete the table below.

5. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
5
October 06, 2014

6. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
6
October 06, 2014
§ In this case the ratio of the number of gallons of red paint to the number of
gallons of yellow paint is 1:3. What if the ratio were changed to 1:4? What would
this mean in the context of our paint problem?
§ Can we still use the equation we created earlier? What would the new equation
be?
§ How can we use the ratio to write the equation?
§ What if the ratio were 1:7? What would the new equation be?

7. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
7
October 06, 2014
Exercise 3
Jorge now plans to mix red paint and blue paint to create purple paint. The color of
purple he has decided to make combines red paint and blue paint in the ratio 4:1. If
Jorge can only purchase paint in one gallon containers, construct a ratio table for all
possible combinations for red and blue paint that will give Jorge no more than 25
gallons of purple paint.

8. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
8
October 06, 2014
Remember that we sometimes use variables to represent numbers. Let’s use B and
R for the amounts of blue paint and red paint, respectively.
No matter how much blue paint I use, I need 4 times as much red paint.
So for one gallon of blue paint, I need (1x4) 4 gallons of red paint. That is a ratio of
1:4. The value of the ratio is 14

9. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
9
October 06, 2014
§ Write an equation that will let Jorge calculate the amount of red paint he will
need for any given amount of blue paint.
§ Write an equation that will let Jorge calculate the amount of blue paint he will
need for any given amount of red paint.
§ If Jorge has 24 gallons of red paint, how much blue paint will he have to use to
create the desired color of purple?
§ If Jorge has 24 gallons of blue paint, how much red paint will he have to use to
create the desired color of purple?

10. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
10
October 06, 2014
Let's take a
look at
tonight's hw.
Open to exit
ticket lesson
13.

11. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
11
October 06, 2014
1.
2. 3.

12. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
12
October 06, 2014
a. Using the same relationship of red to blue, create a table that models the
relationship of the three colors blue, red, and purple (total) paint. Let B
represent the number of gallons of blue paint, let R represent the number of
gallons of red paint, and let T represent the total number of gallons of
(purple) paint. Then write an equation that also models this relationship and
answer the questions.
Equation:
Value of the ratio of Total Paint to Blue Paint:
How is the value of the ratio related to the equation?

13. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
13
October 06, 2014
b. During a particular U.S. Air Force training exercise, the ratio of the number
of men to the number of women was 6:1. Use the ratio table provided below
to create at least two equations (see examples below) that model the
relationship between the number of men and the number of women
participating in this training exercise.
equation for how many men:_______________
equation for how many women:_____________
equation for ratio of men to women: ________
equation for ratio of women to men: ________
If 200 women participated in the training exercise, use one of your equations to
calculate the number of men who participated.

14. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
14
October 06, 2014
c. Malia is on a road trip. During the first five minutes of Malia’s trip,
she sees 18 cars and 6 trucks. Complete the ratio table using this
comparison. Let T represent the number of trucks she sees, and let C
represent the number of cars she sees.
What is the value of the ratio of the number of cars to the
number of trucks?
What equation would model the relationship between cars
and trucks?
At the end of the trip, Malia had counted 1,254 trucks. How
many cars did she see?

15. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
15
October 06, 2014
d. Kevin is training to run a half‐marathon. His training program
recommends that he run for 5 minutes and walk for 1 minute. Let R
represent the number of minutes running, and let W represent the number
of minutes walking.
What is the value of the ratio of the number of minutes walking to the number of
minutes running?
What equation could you use to calculate the minutes spent walking if you know
the minutes spent running?

16. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
16
October 06, 2014
Explain how the value of the ratio can be seen in the table.
The values in the first column show the values in the ratio. The ratio of the
minutes running to the minutes walking is 5:1 . The value of the ratio is 5
Explain how the value of the ratio can be seen in the equation R =5W.
1
The minutes running is represented as R . The minutes walking is represented as W
in the equation. The value is represented because the amount of running is five
times as much as the amount of walking or R = 5W.

17. Module 1 Lesson 13 From Ratio Tables to Equations Using the Value of a Ratio.notebook
17
October 06, 2014
Closing
Please take out your exit ticket for Lesson 13, close your
binder, and complete the exit ticket. This will be collected.