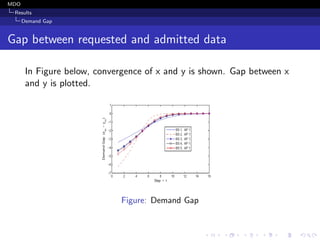
This document provides an overview of mobile data offloading techniques for next generation cellular networks. It discusses the expected growth in mobile data traffic and need for offloading to WiFi networks. It presents a model for the offloading system involving mobile network operators, base stations and access points. It formulates the offloading problem as an optimization to maximize social welfare. An iterated double auction mechanism is proposed to solve the optimization in a distributed manner while achieving the desired economic properties. Results show the mechanism enables the requests and admissions to converge over iterations, minimizing the demand gap.




![MDO
Introduction to MDO
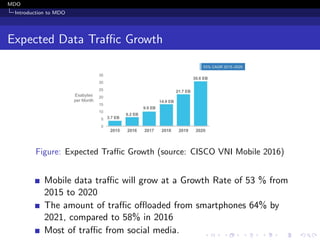
Why MDO?
Huge increase in Wi-Fi enabled devices [Cisco,2016]
Wi-Fi devices: 1.7 Billion
Cellular devices: 548 millions
Can we use these Wi-Fi access points?](https://image.slidesharecdn.com/mobiledataoffloading-180701201742/85/Mobile-data-offloading-6-320.jpg)


![MDO
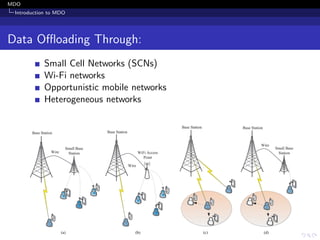
Offloading System Model
Mobile Data Offloading Scenario
Typical offloading system has
A set of MNOs, κ
∆
= {1, 2, ..., K}
A set of BSs, M
∆
= {1, 2, . . . , M}
A set of APs, I
∆
= {1, 2 . . . , I}
Figure: Offloading scenario [Iosifidis, 2015]](https://image.slidesharecdn.com/mobiledataoffloading-180701201742/85/Mobile-data-offloading-10-320.jpg)