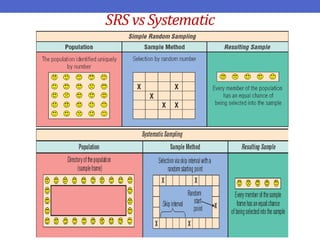
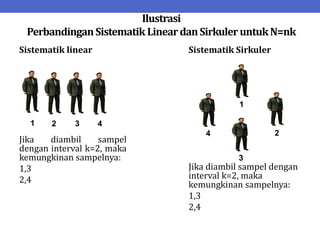
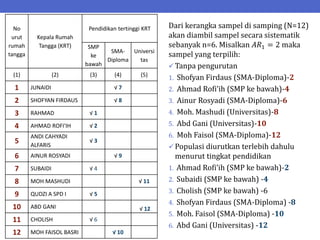
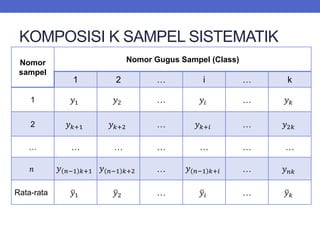
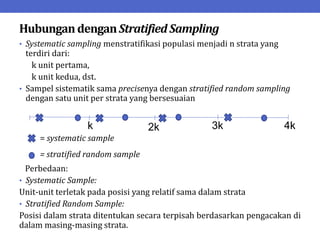
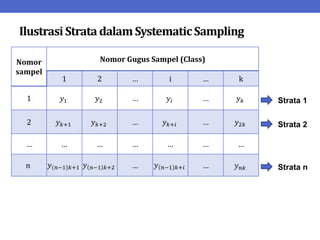
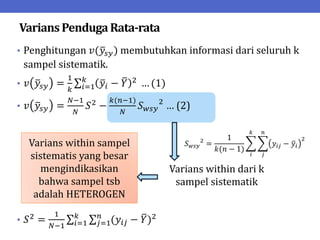
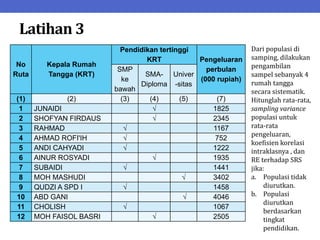
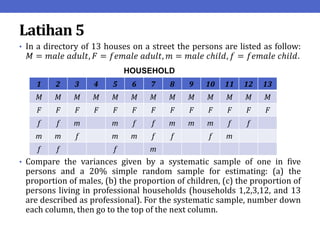
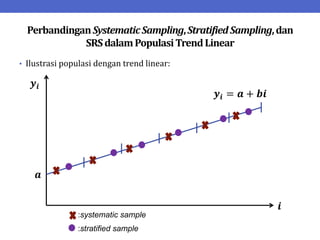
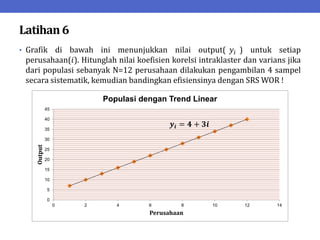
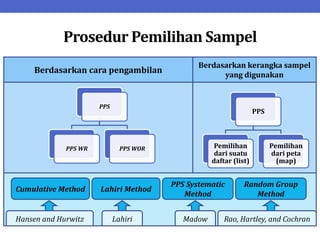
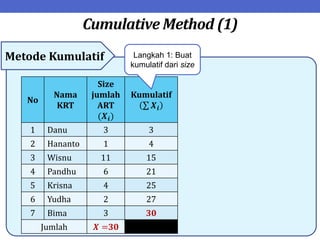
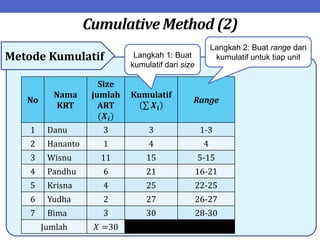
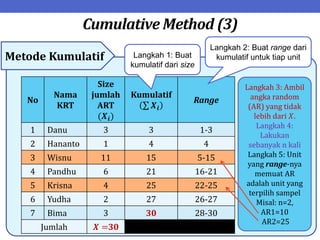
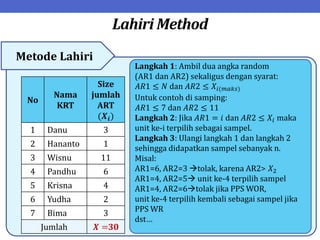
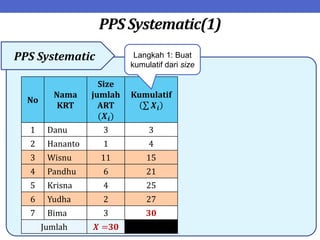
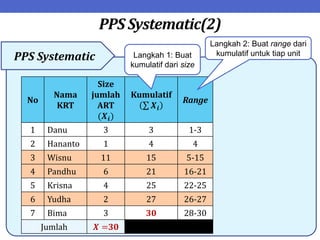
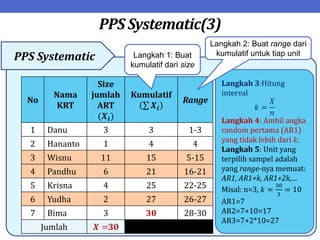
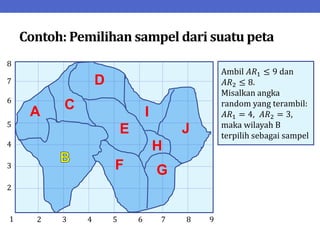
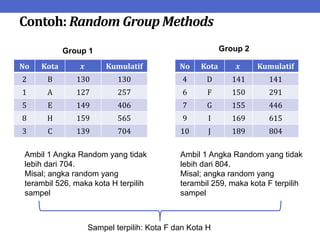
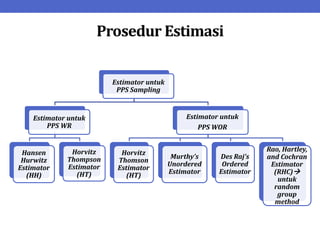
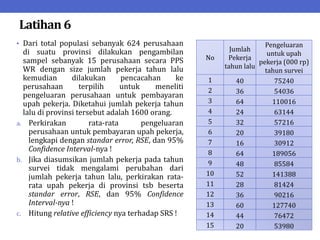
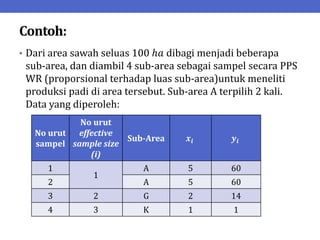
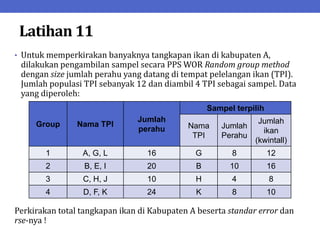
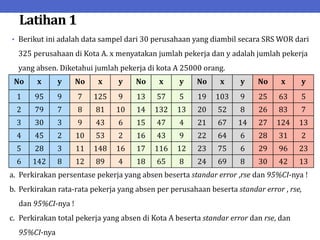
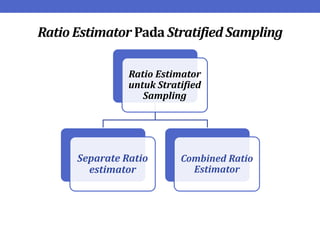
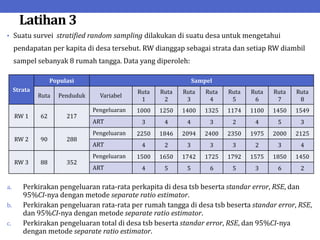
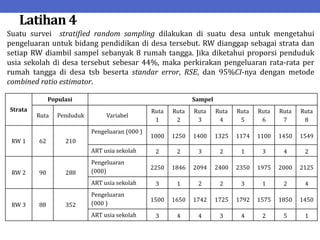
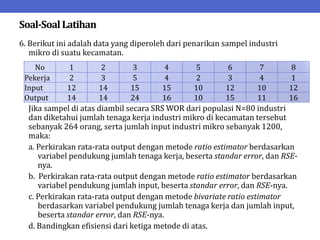
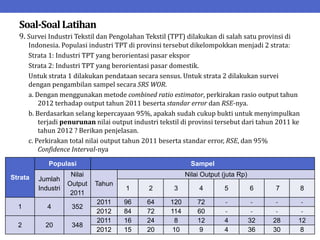
Dokumen ini menjelaskan tentang teknik penarikan sampel sistematik dalam penelitian yang memanfaatkan angka random untuk memilih unit pertama, kemudian mengikuti interval tertentu untuk unit berikutnya. Terdapat dua metode utama, yaitu linear dan circular systematic sampling, masing-masing dengan cara menghitung interval dan mengambil angka random dari tabel. Selain itu, dokumen ini juga membahas masalah yang mungkin muncul dengan interval dan konsep pengaturan unit untuk meningkatkan efisiensi sampling.

1. SYSTEMATIC
RANDOM SAMPLING
Oleh: Adhi Kurniawan
METODE PENARIKAN SAMPEL

2. Pengantar
• Pada penarikan sampel acak sederhana (SRS) setiap unit dipilih dengan
menggunakan angka random.
• Dengan demikian kita harus menarik sampel sebanyak n kali.
• Untuk memperingan penarikan sampel ini maka diterapkan penarikan
sampel secara sistematik, dengan hanya mengambil satu angka random
saja dan lainnya akan mengikuti dengan menghitung interval-nya.
Jadi, systematic sampling adalah suatu teknik sampling di mana
hanya unit pertama dipilih dengan bantuan angka random dan
untuk mendapatkan sampel sisanya dipilih secara otomatis
menurutintervalyangditentukansebelumnya.

3. SRS vs Systematic

4. Prinsip
• N unit dalam populasi diberi nomor urut 1 s/d N
• Ada interval (k) antar unit sampel: 𝑘 =
𝑁
𝑛
• Unit sampel pertama 𝐴𝑅1 dipilih secara acak/random
Cara 1: antara 1-k (Linear Systematic Sampling)
Cara 2: antara 1-N (Circular Systematic Sampling)
• Unit sampel berikutnya ditentukan oleh interval (k), yaitu dengan
menambahkan angka random unit terpilih sebelumnya dengan
interval.
𝐴𝑅𝑛 = 𝐴𝑅𝑛−1 + 𝑘
• Pemilihan unit pertama akan menentukan sampel secara keseluruhan
Misal: N=60; n=10; maka 𝑘 =
60
10
= 6
Jika 𝐴𝑅1 yang terpilih adalah 2 maka sampel terpilihnya:
no: 2,8,14,20,26,32,38,44,50,56
No Mhs 1 2 3 4 5 6 7 8 9 … 60
Tinggi (cm) 165 162 155 176 160 180 176 173 154 … 166

5. Linear Systematic Sampling
a. Hitung interval, yaitu
𝑘 =
𝑁
𝑛
b. Tentukan satu angka random yang lebih kecil atau sama dengan
intervalnya (pilih AR≤ 𝑘) dari tabel angka random
Angka random ini selanjutnya disebut angka random pertama 𝐴𝑅1 .
Unit yang nomor urutnya sama dengan AR ini terpilih sebagai sampel
pertama.
c. Angka random selanjutnya dihitung dengan interval:
𝐴𝑅2 = 𝐴𝑅1 + 𝑘
𝐴𝑅3 = 𝐴𝑅2 + 𝑘 = 𝐴𝑅1 + 2𝑘
𝐴𝑅4 = 𝐴𝑅3 + 𝑘 = 𝐴𝑅1 + 3𝑘
…
𝐴𝑅𝑛 = 𝐴𝑅𝑛−1 + 𝑘 = 𝐴𝑅1 + 𝑛 − 1 𝑘
Unit yang nomor urutnya sama dengan AR di atas terpilih sebagai
sampel.
d. Jika N tidak dapat dinyatakan dalam bentuk N=nk, maka k diambil
sebagai bilangan bulat yang paling dekat dengan N/n.

6. Contoh:PopulasiN=10akandiambilsampeln=3secaralinearsystematic
Baris
Kolom
(1-5)
1 8 8 3 4 7
2 5 7 1 40
3 7 4 6 8 6
4 6 8 0 1 3
5 5 7 4 7 7
1 2 3 4 5 6 7 8 9 10
Langkah 1: Menghitung interval
𝑘 =
𝑁
𝑛
=
10
3
= 3.33 ≈ 3
Langkah 2: Menentukan sampel pertama dengan bantuan
angka random
Misal: 𝐴𝑅1 diambil secara independent choice of digits
dengan permulaan pembacaan TAR baris 1 kolom 4, maka
ambil 𝐴𝑅1 ≤ 𝑘 → 𝐴𝑅1 = 1
Langkah 3: menentukan sampel kedua sampai ketiga
dengan bantuan interval
𝐴𝑅2 = 𝐴𝑅1 + 𝑘 = 1 + 3 = 4
𝐴𝑅3 = 𝐴𝑅2 + 𝑘 = 4 + 3 = 7

7. Circular Systematic Sampling
a. Hitung interval, yaitu
𝑘 =
𝑁
𝑛
b. Tentukan satu angka random yang lebih kecil atau sama dengan populasi (pilih
AR≤ 𝑁) dari tabel angka random. Angka random ini selanjutnya disebut angka
random pertama 𝐴𝑅1 . Unit yang nomor urutnya sama dengan AR ini terpilih
sebagai sampel pertama.
c. Angka random selanjutnya dihitung dengan interval:
𝐴𝑅2 = 𝐴𝑅1 + 𝑘
𝐴𝑅3 = 𝐴𝑅2 + 𝑘 = 𝐴𝑅1 + 2𝑘
𝐴𝑅4 = 𝐴𝑅3 + 𝑘 = 𝐴𝑅1 + 3𝑘
…
𝐴𝑅𝑛 = 𝐴𝑅𝑛−1 + 𝑘 = 𝐴𝑅1 + 𝑛 − 1 𝑘
Unit yang nomor urutnya sama dengan AR di atas terpilih sebagai sampel.
e. Jika setelah ditambahkan dengan interval, didapatkan AR yang lebih besar dengan
nilai populasi (N) maka kurangkan AR tsb dengan nilai N. Unit yang nomor urutnya
sama dengan AR setelah dikurangi N adalah unit yang terpilih sebagai sampel

8. Contoh:PopulasiN=10akandiambilsampeln=3secaracircularsystematic
Baris
Kolom
(1-5)
1 8 8 3 4 7
2 5 7 1 40
3 7 4 6 8 6
4 6 8 0 1 3
5 5 7 4 7 7
1 2 3 4 5 6 7 8 9 10
Langkah 1: Menghitung interval
𝑘 =
𝑁
𝑛
=
10
4
= 3.33 ≈ 3
Langkah 2: Menentukan sampel pertama dengan bantuan
angka random
Misal: 𝐴𝑅1 diambil secara remainder approach dengan
permulaan pembacaan TAR baris 1 kolom 1, maka 𝑁′
= 90,
ambil 𝑎𝑛𝑔𝑘𝑎 𝑟𝑎𝑛𝑑𝑜𝑚 ≤ 𝑁′
→ 𝑎𝑛𝑔𝑘𝑎 𝑟𝑎𝑛𝑑𝑜𝑚 = 88 →
88
10
𝑠𝑖𝑠𝑎 8 → 𝐴𝑅1 = 8
Langkah 3: menentukan sampel kedua sampai ketiga
dengan bantuan interval
𝐴𝑅2 = 𝐴𝑅1 + 𝑘 = 8 + 3 = 11 − 10 = 1
𝐴𝑅3 = 𝐴𝑅2 + 𝑘 = 1 + 3 = 4

9. Latihan 1
• Seorang manajer perusahaan ingin mengetahui tingkat loyalitas pegawainya.
Untuk itu, dari 11 pegawai dilakukan penarikan 4 sampel secara sistematik.
No Nama
1 Bima
2 Yudhistira
3 Pandhu
4 Larasati
5 Joseph
6 Rukmini
7 Sinta
8 Haris
9 Indra
10 Wisnu
11 Krisna
Baris
Kolom
(1-5)
1 88347
2 57140
3 74686
4 68013
5 57477
TAR Tentukan pegawai yang terpilih sampel jika
penarikan sampel dilakukan dengan
1. Sistematik linear
a. Penelusuran 𝐴𝑅1 dari TAR baris 1 kolom
4, independent choice of digits
b. Penelusuran 𝐴𝑅1 dari TAR baris 3 kolom
4, remainder approach
c. Penelusuran 𝐴𝑅1 dari TAR baris 1 kolom
4, quotient approach
2. Sistematik sirkuler
a. Penelusuran 𝐴𝑅1 dari TAR baris 1 kolom
3, independent choice of digits
b. Penelusuran 𝐴𝑅1 dari TAR baris 1 kolom
2, remainder approach
c. Penelusuran 𝐴𝑅1 dari TAR baris 1 kolom
1, quotient approach

10. Ilustrasi
PerbandinganSistematik LineardanSirkuleruntukN=nk
Sistematik linear
Jika diambil sampel
dengan interval k=2, maka
kemungkinan sampelnya:
1,3
2,4
Sistematik Sirkuler
Jika diambil sampel dengan
interval k=2, maka
kemungkinan sampelnya:
1,3
2,4
1 2 3 4
1
2
3
4

11. Ilustrasi
PerbandinganSistematik LineardanSirkuleruntukN≠nk
Sistematik linear
Jika k=3, maka kemungkinan
sampelnya:
1,4
2,5
3
Sistematik Sirkuler
Jika k=3, maka kemungkinan
sampelnya:
1,4 4,2
2,5 5,3
3,1
1 2 3 4 5
1
2
3
4
5

12. Problem WithIntervals(1)
• If the population size N is not an integral multiple of k, a
problem arises. It can be solved in several ways and the
sampler should choose the most convenient.
1. Permit the sample size to be either n or (n+1). Choose
k so that N is greater than nk, but less than (n+1)k. Then,
the random start will determine whether the sample size
will be n or n+1.
2. Eliminate with epsem enough units to reduce the
listings to exactly nk before selection with the interval
k. The probability of selection over the two procedures is
n/N. Instead of elimination, it may be convenient to select
some listings with epsem, then add these duplicates to the
end of the list

13. Problem WithIntervals(2)
3. Consider the list to be circular, so that the last unit is
followed by the first. Choose a random start from 1 to N.
Now add the intervals k until exactly n elements are
choosen, going to the end of the list and then continuing to
the beginning.
4. Using fractional intervals is simple with a decimal
fraction. For example, suppose that to select a sample of
n=100 units from a population of N=925 units, the interval
k=N/n=925/100=9,25 is applied.

14. Implicit Stratification
• Selain untuk mempermudah penarikan sampel, penarikan sampel sistematik
juga dapat meningkatkan efisiensi desain, misal dengan mengadakan
pengaturan unit-unit (systematic arrangement).
• Pengaturan unit-unit berdasarkan karakteristik tertentu memungkinkan
sampel yang terpilih akan memiliki berbagai karakteristik sehingga lebih
representatif.
• Pengaturan unit-unit berdasarkan karakteristik tertentu, kemudian dilakukan
penarikan sampel sistematik ini disebut implicit stratification.
• Pengurutan biasanya didasarkan pada kriteria geografis seperti urban-rural,
administrative region, ethnics subpopulations, atau socioeconomic groups, dsb.
• Keuntungan implicit stratification:
1. Tidak perlu membangun explicit stratification, sampel otomatis akan
teralokasi secara proporsional.
2. Sederhana, hanya memerlukan pengaturan unit-unit dan penggunaan
interval untuk penarikan secara sistematik sampling.
3. Jika kriteria yang dijadikan dasar pengurutan mempunyai korelasi yang kuat
dengan variabel yang diteliti maka akan meningkatkan presisi hasil estimasi

15. Dari kerangka sampel di samping (N=12)
akan diambil sampel secara sistematik
sebanyak n=6. Misalkan 𝐴𝑅1 = 2 maka
sampel yang terpilih:
 Tanpa pengurutan
1. Shofyan Firdaus (SMA-Diploma)-2
2. Ahmad Rofi’ih (SMP ke bawah)-4
3. Ainur Rosyadi (SMA-Diploma)-6
4. Moh. Mashudi (Universitas)-8
5. Abd Gani (Universitas)-10
6. Moh Faisol (SMA-Diploma)-12
 Populasi diurutkan terlebih dahulu
menurut tingkat pendidikan
1. Ahmad Rofi’ih (SMP ke bawah)-2
2. Subaidi (SMP ke bawah) -4
3. Cholish (SMP ke bawah) -6
4. Shofyan Firdaus (SMA-Diploma) -8
5. Moh. Faisol (SMA-Diploma) -10
6. Abd Gani (Universitas) -12
No
urut
rumah
tangga
Kepala Rumah
Tangga (KRT)
Pendidikan tertinggi KRT
SMP
ke
bawah
SMA-
Diploma
Universi
tas
(1) (2) (3) (4) (5)
1 JUNAIDI √ 7
2 SHOFYAN FIRDAUS √ 8
3 RAHMAD √ 1
4 AHMAD ROFI'IH √ 2
5
ANDI CAHYADI
ALFARIS
√ 3
6 AINUR ROSYADI √ 9
7 SUBAIDI √ 4
8 MOH MASHUDI √ 11
9 QUDZI A SPD I √ 5
10 ABD GANI √ 12
11 CHOLISH √ 6
12 MOH FAISOL BASRI √ 10

16. KOMPOSISI K SAMPEL SISTEMATIK
Nomor
sampel
Nomor Gugus Sampel (Class)
1 2 … i … k
1 𝑦1 𝑦2 … 𝑦𝑖 … 𝑦𝑘
2 𝑦𝑘+1 𝑦𝑘+2 … 𝑦𝑘+𝑖 … 𝑦2𝑘
… … … … … … …
𝑛 𝑦 𝑛−1 𝑘+1 𝑦 𝑛−1 𝑘+2 … 𝑦 𝑛−1 𝑘+𝑖 … 𝑦𝑛𝑘
Rata-rata 𝑦1 𝑦2 … 𝑦𝑖 … 𝑦𝑘

17. HubungandenganStratified Sampling
• Systematic sampling menstratifikasi populasi menjadi n strata yang
terdiri dari:
k unit pertama,
k unit kedua, dst.
• Sampel sistematik sama precisenya dengan stratified random sampling
dengan satu unit per strata yang bersesuaian
Perbedaan:
• Systematic Sample:
Unit-unit terletak pada posisi yang relatif sama dalam strata
• Stratified Random Sample:
Posisi dalam strata ditentukan secara terpisah berdasarkan pengacakan di
dalam masing-masing strata.
= systematic sample
= stratified random sample
k 2k 3k 4k

18. Ilustrasi StratadalamSystematicSampling
Nomor
sampel
Nomor Gugus Sampel (Class)
1 2 … i … k
1 𝑦1 𝑦2 … 𝑦𝑖 … 𝑦𝑘
2 𝑦𝑘+1 𝑦𝑘+2 … 𝑦𝑘+𝑖 … 𝑦2𝑘
… … … … … … …
𝑛 𝑦 𝑛−1 𝑘+1 𝑦 𝑛−1 𝑘+2 … 𝑦 𝑛−1 𝑘+𝑖 … 𝑦𝑛𝑘
Strata 1
Strata 2
Strata n

19. HubungandenganClusterSampling
• Dengan N=nk, populasi dibagi menjadi k unit sampling yang besar, yang
masing-masing mengandung n unit original.
• Pelaksanaan pemilihan sampel sistematik adalah pelaksanaan pemilihan
satu dari unit-unit sampling yang besar ini secara acak.
• Sebuah sampel sistematik adalah sebuah sampel acak sederhana dari
satu unit cluster dari suatu populasi sebanyak k unit cluster.
Nomor
sampel
Nomor Gugus Sampel (Class)
1 2 … i … k
1 𝑦1 𝑦2 … 𝑦𝑖 … 𝑦𝑘
2 𝑦𝑘+1 𝑦𝑘+2 … 𝑦𝑘+𝑖 … 𝑦2𝑘
… … … … … … …
𝑛 𝑦 𝑛−1 𝑘+1 𝑦 𝑛−1 𝑘+2 … 𝑦 𝑛−1 𝑘+𝑖 … 𝑦𝑛𝑘
Cluster
1
Cluster
2
Cluster
i
Cluster
k

20. PendugaRata-rataPopulasi
• Linear Systematic Sampling
 Jika N=nkrata-rata sampel dari sebuah sampel sistematik
merupakan penduga unbiased dari rata-rata populasi
 Jika N ≠ nkrata-rata sampel dari sebuah sampel sistematik
merupakan penduga biased dari rata-rata populasi
• Circular Systematic Sampling
(N=nk maupun N≠nk)
 Rata-rata sampel akan selalu merupakan penduga unbiased
Sistematik
Kondisi
N=nk N≠nk
Linear Unbiased Biased
Sirkuler Unbiased Unbiased

21. PendugaRata-rataPopulasi
𝑦𝑖 =
1
𝑛
𝑦𝑖𝑗rata-rata untuk sampel sistematik ke-i
𝐸 𝑦𝑠𝑦 =
1
𝑘
𝑦𝑖
𝑘
𝑖=1
=
1
𝑘
𝑦1 + 𝑦2 + ⋯ + 𝑦𝑘
=
1
𝑘
1
𝑛
𝑦1 + 𝑦1 + ⋯ + 𝑦𝑁 … (𝑗𝑖𝑘𝑎 𝑁 = 𝑛𝑘)
=
1
𝑁
𝑦1 + 𝑦1 + ⋯ + 𝑦𝑁
=
1
𝑁
𝑦𝑖
𝑁
𝑖=1
= 𝑌

22. Latihan2
• Diketahui populasi mahasiswa sebanyak N=9 dengan jumlah buku
sampling yang dimiliki sebagai berikut:
Buktikan secara empiris bahwa penarikan sampel secara sistematik
linear maupun sirkuler (n=3) akan menghasilkan penduga rata-rata yang
unbiased !
• Diketahui populasi mahasiswa sebanyak N=10 dengan jumlah buku
ekonomi yang dimiliki sebagai berikut:
Buktikan secara empiris bahwa penarikan sampel (n=3) secara
sistematik linear akan menghasilkan penduga rata-rata yang biased,
tetapi penarikan sampel secara sistematik sirkuler akan menghasilkan
penduga yang unbiased !
No 1 2 3 4 5 6 7 8 9
Jumlah Buku 1 2 2 3 3 4 5 7 9
No 1 2 3 4 5 6 7 8 9 10
Jumlah Buku 1 1 2 3 3 4 4 5 6 8

23. • Penghitungan 𝑣(𝑦𝑠𝑦) membutuhkan informasi dari seluruh k
sampel sistematik.
• 𝑣 𝑦𝑠𝑦 =
1
𝑘
𝑦𝑖 − 𝑌 2
𝑘
𝑖=1 … (1)
• 𝑣 𝑦𝑠𝑦 =
𝑁−1
𝑁
𝑆2 −
𝑘(𝑛−1)
𝑁
𝑆𝑤𝑠𝑦
2
… (2)
• 𝑆2 =
1
𝑁−1
(𝑦𝑖𝑗 − 𝑌)2
𝑛
𝑗=1
𝑘
𝑖=1
VariansPendugaRata-rata
Varians within dari k
sampel sistematik
Varians within sampel
sistematis yang besar
mengindikasikan
bahwa sampel tsb
adalah HETEROGEN
𝑆𝑤𝑠𝑦
2
=
1
𝑘(𝑛 − 1)
𝑦𝑖𝑗 − 𝑦𝑖
2
𝑛
𝑗
𝑘
𝑖

24. • Misal populasi:
1,2,3,4,5 | 1,2,3,4,5 | 1,2,3,4,5 periodicity
• Misal 2 terpilih sampel dan k=5, sehingga sampel
sistematik: 2,2,2 homogen dan tidak representatif
• Varians within=0 dan 𝑣(𝑦𝑠𝑦) akan besar.
Bagaimana mengukur kehomogenan atau keheterogenan ini ?
INTRACLASS CORRELATION COEFFICIENT

25. INTRACLASS CORRELATION COEFFICIENT
• Ukuran yang menyatakan tingkat kehomogenan
dalam sebuah sampel sistematik di antara
pasangan unit dalam sampel sistematik yang sama
adalah intraclass correlation coefficient (𝜌)
• 𝜌 =
𝐸(𝑦𝑖𝑗−𝑌)(𝑦𝑖𝑗′−𝑌)
𝐸(𝑦𝑖𝑗−𝑌)2
• 𝑣 𝑦𝑠𝑦 =
𝑆2
𝑛
𝑁−1
𝑁
1 + (𝑛 − 1)𝜌

26. INTRACLASS CORRELATION COEFFICIENT
• Ketika ada n unit sampling dalam sebuah sampel sistematik,
maka ada
𝑛
2
=
𝑛(𝑛−1)
2
pasangan unit sampling yang
berbeda yang bisa kita pilih
• Karena keseluruhan ada k sampel sistematis, ada
𝑘𝑛(𝑛−1)
2
pasangan yang berbeda, sehingga:
𝐸 𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌 =
2
𝑘𝑛(𝑛 − 1)
𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌
𝑛
𝑗<𝑗′
𝑘
𝑖=1
𝐸(𝑦𝑖𝑗 − 𝑌)2
=
1
𝑁
(𝑦𝑖𝑗 − 𝑌)2
𝑛
𝑗=1
𝑘
𝑖=1
=
𝑁 − 1
𝑁
1
𝑁 − 1
(𝑦𝑖𝑗 − 𝑌)2
𝑛
𝑗=1
𝑘
𝑖=1
=
𝑁 − 1
𝑁
𝑆2

27. INTRACLASS CORRELATION COEFFICIENT
• 𝜌 =
2
𝑘𝑛(𝑛−1)
𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌 .
𝑁
(𝑁−1)𝑆2
𝑛
𝑗<𝑗′
𝑘
𝑖=1
𝑉 𝑦𝑠𝑦 =
𝑆2
𝑛
𝑁 − 1
𝑁
1 + (𝑛 − 1)𝜌
• Jika 𝜌 besar dan positif 𝑣(𝑦𝑠𝑦) besar (unit-unit
homogen dalam sampel sistematik)
• Jika 𝜌 kecil dan (+/-)  𝑣(𝑦𝑠𝑦) kecil (unit-unit
heterogen dalam sampel sistematik)

28. Pembuktian (1)
Varians cara 1:
𝑽 𝒚𝒔𝒚 = 𝐸 𝑦𝑖 − 𝐸 𝑦𝑖
2
= 𝐸 𝑦𝑖 − 𝑌 2
=
𝟏
𝒌
𝒚𝒊 − 𝒀 𝟐
𝒌
𝒊=𝟏
Varians cara 2:
𝑉 𝑦𝑠𝑦 =
1
𝑘
𝑦𝑖 − 𝑌 2
𝑘
𝑖=1
𝑦𝑖𝑗 − 𝑌
2
= 𝑦𝑖𝑗 − 𝑦𝑖 + 𝑦𝑖 − 𝑌
2
𝑛
𝑗=1
𝑘
𝑖=1
𝑛
𝑗=1
𝑘
𝑖=1
= 𝑦𝑖𝑗 − 𝑦𝑖
2
+ 𝑦𝑖 − 𝑌 2
+ 2 𝑦𝑖𝑗 − 𝑦𝑖 𝑦𝑖 − 𝑌
𝑛
𝑗=1
𝑘
𝑖=1
= 𝑦𝑖𝑗 − 𝑦𝑖
2
𝑛
𝑗=1
+
𝑘
𝑖=1
𝑦𝑖 − 𝑌 2
𝑛
𝑗=1
+
𝑘
𝑖=1
2 𝑦𝑖𝑗 − 𝑦𝑖 𝑦𝑖 − 𝑌
𝑛
𝑗=1
𝑘
𝑖=1

29. Pembuktian (2)
𝑦𝑖 − 𝑌 2
𝑛
𝑗=1
= 𝑛 𝑦𝑖 − 𝑌 2
𝑘
𝑖=1
𝑘
𝑖=1
2 𝑦𝑖𝑗 − 𝑦𝑖 𝑦𝑖 − 𝑌
𝑛
𝑗=1
𝑘
𝑖=1
= 2 𝑦𝑖 − 𝑌 𝑦𝑖𝑗 − 𝑦𝑖
𝑛
𝑗=1
𝑘
𝑖=1
= 0
Sehingga:
𝑦𝑖𝑗 − 𝑌
2
= 𝑛 𝑦𝑖 − 𝑌 2
𝑘
𝑖=1
+ 𝑦𝑖𝑗 − 𝑦𝑖
2
𝑛
𝑗=1
𝑘
𝑖=1
𝑛
𝑗=1
𝑘
𝑖=1
𝑉 𝑦𝑠𝑦 =
1
𝑘𝑛
𝑦𝑖𝑗 − 𝑌
2
−
1
𝑘𝑛
𝑦𝑖𝑗 − 𝑦𝑖
2
𝑛
𝑗=1
𝑘
𝑖=1
𝑛
𝑗=1
𝑘
𝑖=1
Karena:
𝑆𝑤𝑠𝑦
2
=
1
𝑘(𝑛 − 1)
𝑦𝑖𝑗 − 𝑦𝑖
2
𝑛
𝑗
𝑘
𝑖
𝑆2
=
1
𝑁 − 1
(𝑦𝑖𝑗 − 𝑌)2
𝑛
𝑗=1
𝑘
𝑖=1
Sehingga:
𝑉 𝑦𝑠𝑦 =
𝑁 − 1
𝑁
𝑆2
−
𝑘(𝑛 − 1)
𝑁
𝑆𝑤𝑠𝑦
2

30. Pembuktian(3):
Koefisien korelasi intraklass:
𝜌 =
𝐸(𝑦𝑖𝑗 − 𝑌)(𝑦𝑖𝑗′ − 𝑌)
𝐸(𝑦𝑖𝑗 − 𝑌)2
Karena terdapat sebanyak 𝑛 unit sampling untuk setiap gugus sampel, maka
akan terdapat
𝑛
2
=
𝑛(𝑛−1)
2
pasangan unit sampling yang berbeda yang dapat
dipilih. Oleh karena itu, untuk 𝑘 gugus sampel sistematik akan terdapat
𝑘𝑛(𝑛−1)
2
pasangan yang berbeda, sehingga:
𝐸 𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌 =
2
𝑘𝑛(𝑛 − 1)
(𝑦𝑖𝑗 − 𝑌)(𝑦𝑖𝑗′ − 𝑌)
𝑛
𝑗<𝑗′
𝑘
𝑖=1
𝐸(𝑦𝑖𝑗 − 𝑌)2
=
1
𝑁
(𝑦𝑖𝑗 − 𝑌)2
𝑛
𝑗=1
𝑘
𝑖=1
=
𝑁 − 1
𝑁
1
𝑁 − 1
(𝑦𝑖𝑗 − 𝑌)2
𝑛
𝑗=1
𝑘
𝑖=1
=
𝑁 − 1
𝑁
𝑆2

31. Pembuktian(4)
Sehingga:
𝜌 =
2
𝑘𝑛(𝑛 − 1)
𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌 .
𝑁
(𝑁 − 1)𝑆2
𝑛
𝑗<𝑗′
𝑘
𝑖=1
Varians cara 3:
𝑉 𝑦𝑠𝑦 =
1
𝑘
𝑦𝑖 − 𝑌 2
=
1
𝑘
1
𝑛
𝑦𝑖𝑗 − 𝑌
𝑛
𝑗=1
2
𝑘
𝑖=1
𝑘
𝑖=1
=
1
𝑘
1
𝑛2
𝑦𝑖𝑗 − 𝑌
𝑛
𝑗=1
2
𝑘
𝑖=1
=
1
𝑘
1
𝑛2
𝑦𝑖𝑗 − 𝑌
2
+ 2 𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌
𝑛
𝑗<𝑗′
𝑘
𝑖=1
𝑛
𝑗=1
𝑘
𝑖=1
=
1
𝑘
1
𝑛2
𝑦𝑖𝑗 − 𝑌
2
+ 2
𝑛 − 1
2
∙ 𝑁 − 1 𝑆2
𝜌
𝑛
𝑗=1
𝑘
𝑖=1

32. Pembuktian(5)
𝑉 𝑦𝑠𝑦 =
1
𝑘
∙
1
𝑛2
∙ 𝑦𝑖𝑗 − 𝑌
2
+ 𝑛 − 1 ∙ 𝑁 − 1 𝑆2𝜌
𝑛
𝑗=1
𝑘
𝑖=1
=
1
𝑘
∙
1
𝑛2
∙ 𝑁 − 1 𝑆2 + 𝑛 − 1 ∙ 𝑁 − 1 𝑆2𝜌
=
1
𝑛𝑁
(𝑁 − 1)𝑆2 1 + (𝑛 − 1)𝜌
𝑉 𝑦𝑠𝑦 =
𝑆2
𝑛
𝑁 − 1
𝑁
1 + (𝑛 − 1)𝜌

33. EFISIENSI
• 𝑣 𝑦𝑠𝑟𝑠 =
𝑆2
𝑛
𝑁−𝑛
𝑁
• 𝑣 𝑦𝑠𝑦𝑠 =
𝑆2
𝑛
𝑁−1
𝑁
1 + (𝑛 − 1)𝜌
•
𝑣(𝑦𝑠𝑦𝑠)
𝑣(𝑦𝑠𝑟𝑠)
=
(𝑁−1) 1+(𝑛−1)𝜌
𝑛(𝑘−1)
Agar systematic sampling memiliki presisi yang sama
dengan SRS, maka:
(𝑁 − 1) 1 + (𝑛 − 1)𝜌
𝑛(𝑘 − 1)
= 1
𝜌 =
−1
𝑛𝑘 − 1
=
−1
𝑁 − 1

34. EFISIENSI
• Karena N biasanya besar, 𝜌 seharusnya kecil agar
systematic sampling memiliki presisi yang sama
dengan SRS.
• Nilai 𝜌 akan kecil jika unit-unit sampling dalam
populasi didistribusikan secara random, sehingga
𝑣 𝑦𝑠𝑟𝑠 bisa digunakan untuk sistematic sampling

35. PendugaRata-rataPopulasi danVarians(Ringkasan)
Penduga Rumus
Rata-rata 𝑌 =
1
𝑘
𝑦𝑖.
𝑘
𝑖=1
Varians
𝑉 𝑦𝑠𝑦 =
1
𝑘
𝑦𝑖 − 𝑌 2
𝑘
𝑖=1
𝑉 𝑦𝑠𝑦 =
𝑁 − 1
𝑁
𝑆2
−
𝑘(𝑛 − 1)
𝑁
𝑆𝑤𝑠𝑦
2
𝑉 𝑦𝑠𝑦 =
𝑆2
𝑛
𝑁 − 1
𝑁
1 + (𝑛 − 1)𝜌
Keterangan:
𝑆𝑤𝑠𝑦
2
=
1
𝑘(𝑛 − 1)
𝑦𝑖𝑗 − 𝑦𝑖
2
𝑛
𝑗
𝑘
𝑖
𝑆2
=
1
𝑁 − 1
(𝑦𝑖𝑗 − 𝑌)2
𝑛
𝑗=1
𝑘
𝑖=1
𝜌 =
2
𝑘𝑛(𝑛−1)
𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌 .
𝑁
(𝑁−1)𝑆2
𝑛
𝑗<𝑗′
𝑘
𝑖=1

36. Contoh:
Misalkan populasi N=9 dengan nilai karakteristik 𝑌𝑖 sebagai berikut: 1, 2,
3, 4, 5, 6, 7, 8, 9 diambil sampel n=3 secara sistematik sampling.
Maka komposisi sampel sistematiknya:
𝑌 =
1
𝑘
𝑦𝑖 =
1
3
4 + 5 + 6 = 5
𝑘
𝑖=1
No urut
sampel
Gugus Sampel 1 Gugus Sampel 2 Gugus Sampel 3
𝑌1𝑗 𝑌1𝑗
2 𝑌2𝑗 𝑌2𝑗
2 𝑌3𝑗 𝑌3𝑗
2
1 1 1 2 4 3 9
2 4 16 5 25 6 36
3 7 49 8 64 9 81
Total 12 66 15 93 18 126
Rata-rata 4 22 5 31 6 42

37. Penghitungan varians (cara 1):
𝑉 𝑦𝑠𝑦 =
1
𝑘
𝑦𝑖 − 𝑌 2
𝑘
𝑖=1
=
1
3
4 − 5 2
+ 5 − 5 2
+ 6 − 5 2
=
2
3
Penghitungan varians (cara 2):
𝑆𝑤𝑠𝑦
2
=
1
𝑘(𝑛 − 1)
𝑦𝑖𝑗 − 𝑦𝑖
2
𝑛
𝑗
𝑘
𝑖
=
1
3 ∙ 2
18 + 18 + 18 =
54
6
𝑆2
=
1
𝑁 − 1
(𝑦𝑖𝑗 − 𝑌)2
𝑛
𝑗=1
𝑘
𝑖=1
=
60
8
𝑉 𝑦𝑠𝑦 =
𝑁 − 1
𝑁
𝑆2
−
𝑘 𝑛 − 1
𝑁
𝑆𝑤𝑠𝑦
2
=
8
9
∙
60
8
−
3 ∙ 2
9
∙
54
6
=
2
3

38. Penghitungan varians (cara 3):
𝜌 =
2
𝑘𝑛(𝑛−1)
𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌 .
𝑁
(𝑁−1)𝑆2
𝑛
𝑗<𝑗′
𝑘
𝑖=1
Untuk 𝑖 = 1:
𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌 =
𝑛
𝑗<𝑗′ Penghitungan varians (cara 3):
𝜌 =
2
𝑘𝑛(𝑛−1)
𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌 .
𝑁
(𝑁−1)𝑆2
𝑛
𝑗<𝑗′
𝑘
𝑖=1
Untuk 𝑖 = 1:
𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌 = 𝑦11 − 𝑌 𝑦12 − 𝑌 + 𝑦11 − 𝑌 𝑦13 − 𝑌 + 𝑦12 − 𝑌 𝑦13 − 𝑌
𝑛
𝑗<𝑗′
= 1 − 5 4 − 5 + 1 − 5 7 − 5 + 4 − 5 7 − 5 = −6
Dengan cara yang sama, untuk 𝑖 = 2 diperoleh hasil -9 dan untuk 𝑖 = 3 diperoleh hasil -6.
Maka:
𝜌 =
2
𝑘𝑛(𝑛 − 1)
𝑦𝑖𝑗 − 𝑌 𝑦𝑖𝑗′ − 𝑌 .
𝑁
(𝑁 − 1)𝑆2
𝑛
𝑗<𝑗′
𝑘
𝑖=1
=
2
3∙3∙2
−6 − 9 − 6 ∙
9
8
∙
8
60
= −
21
60
𝑉 𝑦𝑠𝑦 =
𝑆2
𝑛
𝑁 − 1
𝑁
1 + (𝑛 − 1)𝜌 =
60/8
3
∙
8
9
∙ 1 + 3 − 1
−21
60
=
2
3

39. Latihan 3
No
Ruta
Kepala Rumah
Tangga (KRT)
Pendidikan tertinggi
KRT Pengeluaran
perbulan
(000 rupiah)
SMP
ke
bawah
SMA-
Diploma
Univer
-sitas
(1) (2) (3) (4) (5) (7)
1 JUNAIDI √ 1825
2 SHOFYAN FIRDAUS √ 2345
3 RAHMAD √ 1167
4 AHMAD ROFI'IH √ 752
5 ANDI CAHYADI √ 1222
6 AINUR ROSYADI √ 1935
7 SUBAIDI √ 1441
8 MOH MASHUDI √ 3402
9 QUDZI A SPD I √ 1458
10 ABD GANI √ 4046
11 CHOLISH √ 1067
12 MOH FAISOL BASRI √ 2505
Dari populasi di
samping, dilakukan
pengambilan
sampel sebanyak 4
rumah tangga
secara sistematik.
Hitunglah rata-rata,
sampling variance
populasi untuk
rata-rata
pengeluaran,
koefisien korelasi
intraklasnya , dan
RE terhadap SRS
jika:
a. Populasi tidak
diurutkan.
b. Populasi
diurutkan
berdasarkan
tingkat
pendidikan.

40. Latihan4
No Jenis pohon
Harga jual
hasil panen
setahun (000
Rp)
1 Pepaya 198
2 Pepaya 197
3 Pepaya 233
4 Pepaya 206
5 Pepaya 276
6 Durian 822
7 Durian 839
8 Durian 707
9 Durian 826
10 Durian 725
11 Jambu 379
12 Jambu 494
13 Jambu 382
14 Jambu 339
15 Jambu 323
16 Jeruk 486
17 Jeruk 515
18 Jeruk 590
19 Jeruk 521
20 Jeruk 417
• Seorang pemilik kebun buah memiliki 4
jenis pohon buah, yaitu pepaya, durian,
jambu, dan jeruk yang masing-masing jenis
terdiri dari 4 pohon. Berdasarkan populasi
di samping, jika dilakukan penarikan
sampel sebanyak 4 pohon, maka:
a. Hitunglah rata-rata dan varians populasi
beserta koefisien korelasi intraklass dari
harga jual hasil panen setahun jika
penarikan sampel secara sistematik.
b. Jika jenis pohon dianggap sebagai strata,
buatlah tabel annovanya kemudian
hitunglah rata-rata dan varians
populasinya.
c. Hitunglah rata-rata dan varians
populasinya jika dilakukan penarikan
sampel secara SRS WOR.
d. Bandingkan efisiensi antara poin (a),
poin (b), dan poin (c).

41. Latihan 5
• In a directory of 13 houses on a street the persons are listed as follow:
𝑀 = 𝑚𝑎𝑙𝑒 𝑎𝑑𝑢𝑙𝑡, 𝐹 = 𝑓𝑒𝑚𝑎𝑙𝑒 𝑎𝑑𝑢𝑙𝑡, 𝑚 = 𝑚𝑎𝑙𝑒 𝑐ℎ𝑖𝑙𝑑, 𝑓 = 𝑓𝑒𝑚𝑎𝑙𝑒 𝑐ℎ𝑖𝑙𝑑.
• Compare the variances given by a systematic sample of one in five
persons and a 20% simple random sample for estimating: (a) the
proportion of males, (b) the proportion of children, (c) the proportion of
persons living in professional households (households 1,2,3,12, and 13
are described as professional). For the systematic sample, number down
each column, then go to the top of the next column.
1 2 3 4 5 6 7 8 9 10 11 12 13
M M M M M M M M M M M M M
F F F F F F F F F F F F F
f f m m f f m m m f f
m m f m m f f f m
f f f m
HOUSEHOLD

42. JENIS-JENISPOPULASI
• Populasi dengan susunan acak (random population)
• Populasi terurut (ordered population)
• Populasi dengan variasi periodik
• Populasi alami (natural population)
• Populasi yang berautokorelasi

43. Populasi denganSusunanAcak
• Jika unit-unit sampling di dalam populasi tersusun secara acak,
unit-unit sampling di dalam sampel juga akan tersusun secara
acak.
• Oleh karena itu, sampel sistematik bisa diperlakukan seolah-olah
adalah sampel acak.
• Sampel yang tersusun secara acak ini akan menjadi heterogen
dan akan memiliki 𝜌 yang kecil maka 𝑣(𝑦𝑠𝑦) kurang lebih akan
sama dengan 𝑣(𝑦𝑠𝑟𝑠) .
• Misal, sampling dari sebuah frame yang disusun secara alfabetik
menurut nama. Jika item yang diukur tidak memiliki hubungan
dengan nama individu, kita bisa mengharapkan systematic
sampling benar-benar equivalent dengan SRS dan memiliki
varians yang hampir sama.

44. Populasi Terurut
• Dalam sebuah populasi terurut, pemilihan sampel sistematik
akan memberikan sampel yang heterogen dan 𝑣(𝑦𝑠𝑦) biasanya
akan lebih kecil daripada 𝑣(𝑦𝑠𝑟𝑠).
• Contoh: menduga produksi jagung dari populasi petani dengan
luas lahan. Petani diurutkan terlebih dahulu menurut luas lahan,
kemudian dipilih sampel secara sistematik. Sampel yang terpilih
akan heterogen dan menghindari kesempatan memilih sampel
yang mengandung terlalu banyak petani besar/kecil sehingga
lebih mewakili populasi daripada ketika masih tersusun secara
acak.

45. PerbandinganSystematicSampling,StratifiedSampling,dan
SRSdalamPopulasiTrendLinear
• Ilustrasi populasi dengan trend linear:
𝒚𝒊
𝒊
𝒚𝒊 = 𝒂 + 𝒃𝒊
𝒂
:systematic sample
:stratified sample

46. PerbandinganSystematicSampling,StratifiedSampling,dan
SRSdalamPopulasiTrendLinear
𝑌 =
1
𝑁
𝑦𝑖 =
𝑁
𝑖=1
1
𝑁
𝑎 + 𝑏𝑖 = 𝑎 + 𝑏(𝑁 + 1)/2
𝑁
𝑖=1
𝑆2
=
1
𝑁 − 1
𝑦𝑖 − 𝑌 2
=
𝑏2
(𝑁 − 1)
𝑖 −
𝑁 + 1
2
2
𝑁
𝑖=1
𝑁
𝑖=1
=
𝑁(𝑁 + 1)𝑏2
12
=
𝑛𝑘(𝑛𝑘 + 1)𝑏2
12
𝑉
𝑠𝑟𝑠 =
(𝑁 − 𝑛)
𝑁𝑛
∙ 𝑆2
=
𝑘 − 1
𝑛𝑘
∙
𝑛𝑘 𝑛𝑘 + 1
12
∙ 𝑏2
= 𝑘 − 1
𝑛𝑘 + 1
12
𝑏2
𝑉𝑠𝑡𝑟 =
𝑁 − 𝑛
𝑁𝑛
∙ 𝑆𝑤
2
=
𝑘 − 1
𝑛𝑘
∙
𝑘 𝑘 + 1
12
∙ 𝑏2
= (𝑘 − 1)
(𝑘 + 1)
12𝑛
𝑏2
𝑉
𝑠𝑦𝑠 =
1
𝑘
𝑦𝑖 − 𝑌 2
=
1
𝑘
∙
𝑘 𝑘 + 1 𝑘 − 1
12
∙ 𝑏2
= 𝑘 − 1
𝑘 + 1
12
𝑏2
𝑘
𝑖=1
Sehingga:
𝑉𝑠𝑡𝑟 ∶ 𝑉
𝑠𝑦𝑠 ∶ 𝑉
𝑠𝑟𝑠 =
(𝑘 + 1)
𝑛
: 𝑘 + 1 : 𝑛𝑘 + 1 ≅
1
𝑛
: 1: 𝑛 = 1: 𝑛: 𝑛2

47. Populasi denganVariasiPeriodik
• Jika populasi mengandung trend periodik (misalkan kurva sinus),
keefektifan sampel sistematik tergantung pada nilai interval.
• Contoh populasi hipotetik:
1,2,3,4,5| 1,2,3,4,5| 1,2,3,4,5
Jika diambil 3 sampel dan dengan random start 2 dan k=5, maka
sampel sistematiknya: (2,2,2)homogen, 𝜌 besar
• Contoh praktis:
Penjualan tinggihari Jumat dan Sabtu
Penjualan rendahhari Senin dan Selasa
Sampel-sampel bisa dipilih dengan mengubah posisi unit-unit
sampling setiap waktu.

48. Natural Population danAutocorrelated Population
• Systematic sampling secara operasional sangat mudah dan efisien
digunakan dalam populasi alami (natural population), misalnya pada
populasi di area hutan untuk mengestimasi produksi kayu, karet, dsb
• Pada beberapa populasi alami, unit-unit yang berdekatan akan
mempunyai korelasi yang kuat daripada unit-unit yang saling berjauhan.
Populasi semacam ini disebut autocorrelated population.
• Misalnya, 𝑦𝑖 dan 𝑦𝑗 (𝑖 = 1,2, … , 𝑁) adalah nilai observasi dari dari dua
unit yang berkorelasi positif dan serial correlation coefficient 𝜌𝑑 adalah
fungsi dari jarak antara keduanya: 𝑑 = 𝑦𝑖 − 𝑦𝑗.
• Misalkan 𝑦𝑖 diambil dari infinite population (superpopulation) dengan
rata-rata 𝜇 dan varians 𝜎2
maka:
𝐸 𝑦𝑖 = 𝜇 dan 𝐸 𝑦𝑖 − 𝜇 2
= 𝜎2
𝜌𝑑 =
𝐸 𝑦𝑖 − 𝜇 𝑦𝑗 − 𝜇
𝜎2
Untuk 𝑖 = 1,2, … , 𝑁 dan 𝑑 = 1,2, … , (𝑁 − 1)

49. Latihan6
• Grafik di bawah ini menunjukkan nilai output( 𝑦𝑖 ) untuk setiap
perusahaan(𝑖). Hitunglah nilai koefisien korelsi intraklaster dan varians jika
dari populasi sebanyak N=12 perusahaan dilakukan pengambilan 4 sampel
secara sistematik, kemudian bandingkan efisiensinya dengan SRS WOR !
0
5
10
15
20
25
30
35
40
45
0 2 4 6 8 10 12 14
Output
Perusahaan
Populasi dengan Trend Linear
𝒚𝒊 = 𝟒 + 𝟑𝒊

50. EstimasiVariansSistematikdariSingle Sample
• Pada prinsipnya, varians systematic sampling yang unbiased sulit
didapatkan dari sampel sistematik tunggal. Untuk itu, systematic
sampling dapat diasumsikan ke dalam model tertentu sehingga bisa
dilakukan pendekatan dalam penghitungan estimasi sampling varians.
• Ada beberapa pendekatan untuk menghitung estimasi varians
berdasarkan sampel sistematik tunggal yaitu:
1. Simple Random Sampling
2. Stratified Random Sampling
3. Paired Selection Models
4. Succesive Difference Models
5. Interpenetrating (Repeated) Systematic Sampling

51. PendekatanSRSdanStratified Sampling
• Pendekatan SRS:
Jika populasi tersusun secara acak, maka unit-unit yang terpilih dalam
pengambilan sampel sistematik juga akan tersusun acak sehingga dalam kasus
ini estimasi variansnya bisa dilakukan dengan pendekatan SRS, yaitu:
𝑣 𝑦𝑠𝑦 = (1 − 𝑓) ∙
𝑠2
𝑛
• Pendekatan Stratified Random Sampling:
Jika populasi tersusun terurut berdasarkan kategori tertentu (misalkan:
wilayah geografis seperti urban-rural, desa, kecamatan, dsb, karakteristik
demografi seperti jenis kelamin, kelompok umur, dsb, karakteristik sosial
ekonomi seperti kategori pengeluaran, tingkat pendidikan, dsb), maka jumlah
sampel sistematik yang terpilih untuk setiap kategori akan proporsional
terhadap jumlah populasi pada kategori yang bersangkutan. Untuk kasus
seperti ini, varians sampling sistematik bisa didekati dengan rumus varians
proportional stratified sampling, yaitu:
𝑣 𝑦𝑠𝑦 =
𝑁ℎ
𝑁
2
1 − 𝑓ℎ
𝑠ℎ
2
𝑛ℎ
𝐿
ℎ=1

52. Paired Selection Model (PSM)
• Mengelompokkan N unit populasi ke dalam
𝑛
2
kelompok.
• Masing-masing kelompok terdiri dari 2𝑘 unit.
• Melakukan penarikan sampel 2 unit dari tiap kelompok dengan
prosedur:
a. Hitung interval 𝑘′
= 2𝑘 =
2𝑁
𝑛
b. Ambil dua angka random (𝐴𝑅1dan 𝐴𝑅2) yang kurang dari atau sama
dengan 𝑘′
untuk menentukan dua unit yang terpilih sebagai sampel
pertama
c. Sampel selanjutnya ditentukan dengan interval 𝑘′
𝐴𝑅3 = 𝐴𝑅1 + 2𝑘 𝐴𝑅4 = 𝐴𝑅2 + 2𝑘
𝐴𝑅5 = 𝐴𝑅3 + 2𝑘 𝐴𝑅6 = 𝐴𝑅4 + 2𝑘
𝐴𝑅7 = 𝐴𝑅5 + 2𝑘 𝐴𝑅8 = 𝐴𝑅6 + 2𝑘
… …

53. Paired Selection Model (PSM)
Penghitungan varians:
1 2 3 4 5 6 … n-1 n
a. Jika n genap
𝑣 𝑦𝑠𝑦 =
1 − 𝑓
𝑛2
𝑦2𝑖 − 𝑦2𝑖−1
2
𝑛/2
𝑖=1
b. Jika n ganjil
Pilih satu unit secara acak dan menggunakannya dua kali.
𝑣 𝑦𝑠𝑦 =
1 − 𝑓
𝑛(2𝑚)
𝑦2𝑖 − 𝑦2𝑖−1
2
𝑛/2
𝑖=1
Keterangan: 𝑚 =
𝑛+1
2
𝑦2 − 𝑦1
2
𝑦4 − 𝑦3
2
𝑦6 − 𝑦5
2 𝑦𝑛 − 𝑦𝑛−1
2

54. Succesive Difference Model (SDM)
• Metode ini menggunakan semua succesive difference yaitu sebanyak
(n-1) succesive difference, sehingga penghitungan dengan metode ini
variansnya cenderung meningkat.
• Penghitungan varians:
1 2 3 4 5 6 … n-1 n
𝑣 𝑦𝑠𝑦 =
1 − 𝑓
2𝑛(𝑛 − 1)
𝑦𝑖+1 − 𝑦𝑖
2
𝑛−1
𝑖=1
𝑦2 − 𝑦1
2
𝑦4 − 𝑦3
2
𝑦6 − 𝑦5
2 𝑦𝑛 − 𝑦𝑛−1
2
𝑦3 − 𝑦2
2
𝑦5 − 𝑦4
2

55. Interpenetrating (Replicated) SystematicSampling
• Misalnya, suatu sampel sebanyak 𝑛 akan diambil dari populasi sebanyak 𝑁 secara
sistematik. Proses pengambilan sampel yaitu dengan mengambil subsample
sistematik sebanyak 𝑚 gugus sampel dengan independent random starts, masing-
masing memuat 𝑛/𝑚 unit untuk menjaga total sampel sebanyak 𝑛. Anggap 𝑛′
=
𝑛
𝑚
dan 𝑘′
= 𝑚𝑘 maka komposisi sampel sistematiknya:
Nomor
sampel
Nomor Gugus Sampel (Class)
1 2 … i … 𝑘′
1 𝑦1 𝑦2 … 𝑦𝑖 … 𝑦𝑘′
2 𝑦𝑘′+1 𝑦𝑘′+2 … 𝑦𝑘′+𝑖 … 𝑦2𝑘′
… … … … … … …
𝑛′ 𝑦 𝑛′−1 𝑘′+1 𝑦 𝑛′−1 𝑘′+2 … 𝑦 𝑛′−1 𝑘′+𝑖 … 𝑦𝑛′𝑘′
𝑦𝑠𝑦 =
1
𝑚
𝑦𝑖
𝑚
𝑖=1
𝑣 𝑦𝑠𝑦 =
𝑘′
− 𝑚
𝑘′𝑚(𝑚 − 1)
𝑦𝑖 − 𝑦𝑠𝑦
2
𝑚
𝑖=1

56. Stratified SystematicSampling
• Populasi terlebih dahulu dikelompokkan menjadi beberapa strata,
kemudian dari masing-masing strata dilakukan penarikan sampel secara
sistematik.
• Jika 𝑦𝑠𝑦ℎ adalah rata-rata dari sampel sistematik di strata ke-h, estimasi
rata-rata populasi beserta variansnya adalah:
𝑦𝑠𝑡𝑠𝑦 = 𝑊ℎ𝑦𝑠𝑦ℎ
𝐿
ℎ=1
𝑉 𝑦𝑠𝑡𝑠𝑦 = 𝑊ℎ
2
𝑣 𝑦𝑠𝑦ℎ
𝐿
ℎ=1

57. TERIMA KASIH
Have A Nice Sampling

58. PROBABILITY PROPORTIONAL TO
SIZE (PPS SAMPLING)
Oleh: Adhi Kurniawan
METODE PENARIKAN SAMPEL

59. Pengertian
• Pada acak sederhana penarikan sampel hanya didasarkan pada nomor urut
unit dalam populasi.
• Penarikan acak sederhana ini menjadi kurang baik bila unit dalam populasi
ukurannya bervariasi. Oleh karena itu digunakan variabel pendukung
(auxiliary variable) sebagai dasar pertimbangan di dalam penarikan sampel
agar diperoleh estimator yang lebih efisien.
• Variabel pendukung yang digunakan sebagai dasar penarikan sampel
adalah variabel yang memiliki korelasi yang erat dengan variabel yang akan
diteliti.
• Variabel pendukung yang dipertimbangkan sebagai dasar penarikan sampel
selanjutnya disebut ukuran (size).
Prosedur penarikan sampel dimana peluang terpilihnya suatu unit sampel
sebanding dengan ukuran disebut sebagai sampling berpeluang sebanding
dengan ukuran unit atau sampling with probability proportional to size atau
disingkat pps sampling

60. Variabel yang diteliti Variabel pendukung/bantu
 Penduduk sekarang  Penduduk tahun sebelumnya
 Jumlah kelahiran sekarang  Jumlah WUS tahun sebelumnya
 Total panen  Luas lahan yang ditanami
 Total output  Total input
 Produksi pabrik  Jumlah pekerja
Beberapa contoh variabel yang diteliti dan variabel
pendukung

61. Keuntungan
1. Memberikan penduga rata-rata populasi yang unbiased.
2. Mempunyai ketepatan yang lebih tinggi daripada metode-metode
yang lain.
3. Memberikan penduga rata-rata dan varians populasi yang sangat
sederhana.

62. Prosedur Pemilihan Sampel
PPS
PPS WR PPS WOR
PPS
Pemilihan
dari suatu
daftar (list)
Pemilihan
dari peta
(map)
Berdasarkan cara pengambilan
Berdasarkan kerangka sampel
yang digunakan
Cumulative Method Lahiri Method
PPS Systematic
Method
Random Group
Method
Hansen and Hurwitz Lahiri Madow Rao, Hartley, and Cochran

63. Cumulative Method (1)
Metode Kumulatif
No
Nama
KRT
Size
jumlah
ART
(𝑿𝒊)
Kumulatif
𝑿𝒊
1 Danu 3 3
2 Hananto 1 4
3 Wisnu 11 15
4 Pandhu 6 21
5 Krisna 4 25
6 Yudha 2 27
7 Bima 3 30
Jumlah 𝑿 =30
Langkah 1: Buat
kumulatif dari size

64. Cumulative Method (2)
Metode Kumulatif
No
Nama
KRT
Size
jumlah
ART
(𝑿𝒊)
Kumulatif
𝑿𝒊
Range
1 Danu 3 3 1-3
2 Hananto 1 4 4
3 Wisnu 11 15 5-15
4 Pandhu 6 21 16-21
5 Krisna 4 25 22-25
6 Yudha 2 27 26-27
7 Bima 3 30 28-30
Jumlah 𝑋 =30
Langkah 1: Buat
kumulatif dari size
Langkah 2: Buat range dari
kumulatif untuk tiap unit

65. Cumulative Method (3)
Metode Kumulatif
No
Nama
KRT
Size
jumlah
ART
(𝑿𝒊)
Kumulatif
𝑿𝒊
Range
1 Danu 3 3 1-3
2 Hananto 1 4 4
3 Wisnu 11 15 5-15
4 Pandhu 6 21 16-21
5 Krisna 4 25 22-25
6 Yudha 2 27 26-27
7 Bima 3 30 28-30
Jumlah 𝑿 =30
Langkah 3: Ambil
angka random
(AR) yang tidak
lebih dari 𝑋.
Langkah 4:
Lakukan
sebanyak n kali
Langkah 5: Unit
yang range-nya
memuat AR
adalah unit yang
terpilih sampel
Misal: n=2,
AR1=10
AR2=25
Langkah 1: Buat
kumulatif dari size
Langkah 2: Buat range dari
kumulatif untuk tiap unit

66. Latihan 1
• Berikut ini adalah daftar nama desa/kelurahan beserta muatan jumlah
penduduk (dalam 00) di Kecamatan Umbulharjo(040) dan
Kotagede(050), Kota Yogyakarta
No
Desa/Kelurahan Jumlah
Penduduk
Kode Nama
1 3471040001 Giwangan 83
2 3471040002 Sorosutan 160
3 3471040003 Pandeyan 143
4 3471040004 Warungboto 115
5 3471040005 Tahunan 98
6 3471040006 Mujamuju 114
7 3471040007 Semaki 52
8 3471050001 Prenggan 106
9 3471050002 Purbayan 89
10 3471050003 Rejowinangun 114
Lakukan penarikan
sampel sebanyak 4 desa
secara PPS WR dengan
metode kumulatif
Gunakan TAR halaman
1 baris 1 kolom 1,
independent choice of
digits

67. Lahiri Method
Metode Lahiri
No
Nama
KRT
Size
jumlah
ART
(𝑿𝒊)
1 Danu 3
2 Hananto 1
3 Wisnu 11
4 Pandhu 6
5 Krisna 4
6 Yudha 2
7 Bima 3
Jumlah 𝑿 =30
Langkah 1: Ambil dua angka random
(AR1 dan AR2) sekaligus dengan syarat:
𝐴𝑅1 ≤ 𝑁 dan 𝐴𝑅2 ≤ 𝑋𝑖(𝑚𝑎𝑘𝑠)
Untuk contoh di samping:
𝐴𝑅1 ≤ 7 dan 𝐴𝑅2 ≤ 11
Langkah 2: Jika 𝐴𝑅1 = 𝑖 dan 𝐴𝑅2 ≤ 𝑋𝑖 maka
unit ke-i terpilih sebagai sampel.
Langkah 3: Ulangi langkah 1 dan langkah 2
sehingga didapatkan sampel sebanyak n.
Misal:
AR1=6, AR2=3 tolak, karena AR2> 𝑋2
AR1=4, AR2=5 unit ke-4 terpilih sampel
AR1=4, AR2=6tolak jika PPS WOR,
unit ke-4 terpilih kembali sebagai sampel jika
PPS WR
dst…

68. Latihan 2
• Berikut ini adalah daftar nama desa/kelurahan beserta muatan jumlah
penduduk (dalam 00) di Kecamatan Umbulharjo(040) dan
Kotagede(050), Kota Yogyakarta
Lakukan penarikan
sampel sebanyak 4 desa
secara PPS WR dengan
metode Lahiri. Gunakan
TAR halaman 1 baris 1
kolom 1, remainder
approach.
No
Desa/Kelurahan Jumlah
Penduduk
Kode Nama
1 3471040001 Giwangan 83
2 3471040002 Sorosutan 160
3 3471040003 Pandeyan 143
4 3471040004 Warungboto 115
5 3471040005 Tahunan 98
6 3471040006 Mujamuju 114
7 3471040007 Semaki 52
8 3471050001 Prenggan 106
9 3471050002 Purbayan 89
10 3471050003 Rejowinangun 114

69. PPS Systematic(1)
PPS Systematic
No
Nama
KRT
Size
jumlah
ART
(𝑿𝒊)
Kumulatif
𝑿𝒊
1 Danu 3 3
2 Hananto 1 4
3 Wisnu 11 15
4 Pandhu 6 21
5 Krisna 4 25
6 Yudha 2 27
7 Bima 3 30
Jumlah 𝑿 =30
Langkah 1: Buat
kumulatif dari size

70. PPS Systematic(2)
PPS Systematic
No
Nama
KRT
Size
jumlah
ART
(𝑿𝒊)
Kumulatif
𝑿𝒊
Range
1 Danu 3 3 1-3
2 Hananto 1 4 4
3 Wisnu 11 15 5-15
4 Pandhu 6 21 16-21
5 Krisna 4 25 22-25
6 Yudha 2 27 26-27
7 Bima 3 30 28-30
Jumlah 𝑿 =30
Langkah 1: Buat
kumulatif dari size
Langkah 2: Buat range dari
kumulatif untuk tiap unit

71. PPS Systematic(3)
PPS Systematic
No
Nama
KRT
Size
jumlah
ART
(𝑿𝒊)
Kumulatif
𝑿𝒊
Range
1 Danu 3 3 1-3
2 Hananto 1 4 4
3 Wisnu 11 15 5-15
4 Pandhu 6 21 16-21
5 Krisna 4 25 22-25
6 Yudha 2 27 26-27
7 Bima 3 30 28-30
Jumlah 𝑿 =30
Langkah 3:Hitung
interval
𝑘 =
𝑋
𝑛
Langkah 4: Ambil angka
random pertama (AR1)
yang tidak lebih dari 𝑘.
Langkah 5: Unit yang
terpilih sampel adalah
yang range-nya memuat:
AR1, AR1+k, AR1+2k,…
Misal: n=3, 𝑘 =
30
3
= 10
AR1=7
AR2=7+10=17
AR3=7+2*10=27
Langkah 1: Buat
kumulatif dari size
Langkah 2: Buat range dari
kumulatif untuk tiap unit

72. Latihan 3
• Berikut ini adalah daftar nama desa/kelurahan beserta muatan jumlah
penduduk (dalam 00) di Kecamatan Umbulharjo(040) dan
Kotagede(050), Kota Yogyakarta
Lakukan penarikan
sampel sebanyak 4 desa
secara PPS WOR dengan
metode PPS Systematic.
Gunakan TAR halaman
1 baris 1 kolom 1,
quotient approach.
No
Desa/Kelurahan Jumlah
Penduduk
Kode Nama
1 3471040001 Giwangan 83
2 3471040002 Sorosutan 160
3 3471040003 Pandeyan 143
4 3471040004 Warungboto 115
5 3471040005 Tahunan 98
6 3471040006 Mujamuju 114
7 3471040007 Semaki 52
8 3471050001 Prenggan 106
9 3471050002 Purbayan 89
10 3471050003 Rejowinangun 114

73. Pemilihan dari Suatu Peta (MAP)
• Prosedur ini digunakan jika kerangka sampel berupa peta (map)
• Peluang unit-unit wilayah geografis dari sebuah peta untuk
terpilih sebagai sampel sebanding dengan luas (area) dari unit-
unit tersebut  Probability Proportional to Area.
• Prosedur:
1. Ambil dua angka random sekaligus, yaitu:
AR1: antara 1 sampai panjang peta
AR2: antara 1 sampai lebar peta
2. Sepasang angka random terpilih akan menempatkan suatu titik
pada peta, dan wilayah dimana titik itu jatuh adalah wilayah
yang terpilih sebagai sampel
3. Ulangi langkah ke-1 dan ke-2 hingga n unit sampel terpilih.

74. Contoh: Pemilihan sampel dari suatu peta
1 2 3 4 5 6 7 8 9
2
3
4
5
6
7
8
F G
H
E
C
A
D
I
J
Ambil 𝐴𝑅1 ≤ 9 dan
𝐴𝑅2 ≤ 8.
Misalkan angka
random yang terambil:
𝐴𝑅1 = 4, 𝐴𝑅2 = 3,
maka wilayah B
terpilih sebagai sampel

75. Random Group Method
• Random group method merupakan salah satu cara
pengambilan sampel PPS secara wor yang disarankan oleh
Rao, Hartley, dan Cochran (RHC).
• Populasi sebanyak N dibagi menjadi n kelompok, kemudian
dari masing-masing kelompok diambil satu unit sebagai
sampel.
• Dengan demikian, akan terdapat jumlah sampel sebanyak n
unit.

76. Contoh: Random Group Methods
• Berikut adalah daftar 10 kota dilengkapi dengan jumlah
penduduk (dalam ribu jiwa). Akan dipiliih 2 kota sebagai sampel
secara PPS size jumlah penduduk dengan random group method
No Kota Penduduk
1 A 127
2 B 130
3 C 139
4 D 141
5 E 149
6 F 150
7 G 155
8 H 159
9 I 169
10 J 189
No Kota Penduduk
2 B 130
1 A 127
5 E 149
8 H 159
3 C 139
4 D 141
6 F 150
7 G 155
9 I 169
10 J 189
Randomisasi Group 1
Group 2

77. Contoh: Random Group Methods
No Kota 𝒙 Kumulatif
4 D 141 141
6 F 150 291
7 G 155 446
9 I 169 615
10 J 189 804
No Kota 𝒙 Kumulatif
2 B 130 130
1 A 127 257
5 E 149 406
8 H 159 565
3 C 139 704
Group 1 Group 2
Ambil 1 Angka Random yang tidak
lebih dari 704.
Misal; angka random yang
terambil 526, maka kota H terpilih
sampel
Ambil 1 Angka Random yang tidak
lebih dari 804.
Misal; angka random yang
terambil 259, maka kota F terpilih
sampel
Sampel terpilih: Kota F dan Kota H

78. Prosedur Estimasi
Estimator untuk
PPS Sampling
Estimator untuk
PPS WR
Hansen
Hurwitz
Estimator
(HH)
Horvitz
Thompson
Estimator
(HT)
Estimator untuk
PPS WOR
Horvitz
Thomson
Estimator
(HT)
Murthy’s
Unordered
Estimator
Des Raj’s
Ordered
Estimator
Rao, Hartley,
and Cochran
Estimator
(RHC)
untuk
random
group
method

79. Estimator untuk PPS WR
(Hansen Hurwitz Estimator)
• Jika pengambilan sampel dilakukan dengan PPS WR, maka
peluang terpilihnya unit ke-i adalah:
𝑝𝑖 =
𝑋𝑖
𝑋𝑖
𝑁
𝑖=1
=
𝑋𝑖
𝑋
Keterangan:
𝑋𝑖 : nilai dari variabel pendukung (ukuran/size)
• Fraksi sampling/inclusion probability merupakan perkalian
antara 𝑝𝑖 dengan jumlah sampel (𝑛)
𝑓 = 𝜋𝑖 = 𝑝𝑖 ∙ 𝑛 =
𝑋𝑖
𝑋
𝑛
• Sampling weight (penimbang sampling) merupakan kebalikan
(invers) dari fraksi sampling:
𝑤 =
1
𝑓
=
𝑋
𝑛𝑋𝑖

80. Estimator untuk PPS WR
(Hansen Hurwitz Estimator)
• Unbiased estimator untuk total karakteristik Y adalah:
𝑌𝑝𝑝𝑠 = 𝑤 ∙ 𝑦𝑖 =
𝑋
𝑛𝑋𝑖
∙ 𝑦𝑖 =
1
𝑛
𝑦𝑖
𝑝𝑖
𝑛
𝑖=1
𝑛
𝑖=1
𝑛
𝑖=1
Bukti:
Misal 𝑡𝑖 menunjukkan berapa kali unit ke-i akan terpilih dari
pengambilan sampel sebanyak n (i=1,2,…,n)
Maka, joint distribution dari 𝑡𝑖 mengikuti sebaran multinomial:
𝑛!
𝑡1! 𝑡2! … 𝑡𝑁!
𝑝1
𝑡1
𝑝2
𝑡2
… 𝑝𝑁
𝑡𝑁
Untuk sebaran multinomial, properties sebaran dari 𝑡𝑖 diketahui,
yaitu:
𝐸 𝑡𝑖 = 𝑛𝑝𝑖 𝑉 𝑡𝑖 = 𝑛𝑝𝑖 1 − 𝑝𝑖 𝐶𝑜𝑣 𝑡𝑖𝑡𝑗 = −𝑛𝑝𝑖𝑝𝑗

81. Estimator untuk PPS WR
(Hansen Hurwitz Estimator)
• Sehingga rumus estimasi total tersebut bisa dijabarkan:
𝑌𝑝𝑝𝑠 =
1
𝑛
𝑦𝑖
𝑝𝑖
𝑛
𝑖=1
=
1
𝑛
𝑡1
𝑦1
𝑝1
+ 𝑡2
𝑦2
𝑝2
+ ⋯ + 𝑡𝑁
𝑦𝑁
𝑝𝑁
=
1
𝑛
𝑡𝑖
𝑦𝑖
𝑝𝑖
𝑁
𝑖=1
𝐸 𝑌𝑝𝑝𝑠 =
1
𝑛
𝑛𝑝𝑖
𝑦𝑖
𝑝𝑖
= 𝑦𝑖 = 𝑌
𝑁
𝑖=1
𝑁
𝑖=1
(𝑢𝑛𝑏𝑖𝑎𝑠𝑒𝑑)

82. Estimator untuk PPS WR
(Hansen Hurwitz Estimator)
• Varians populasi untuk total karakteristik:
𝑉 𝑌𝑝𝑝𝑠 =
1
𝑛
𝑝𝑖
𝑦𝑖
𝑝𝑖
− 𝑌
2
𝑁
𝑖=1
Bukti:
𝑉 𝑌𝑝𝑝𝑠 =
1
𝑛2
𝑦𝑖
𝑝𝑖
2
𝑉 𝑡𝑖 + 2
𝑦𝑖
𝑝𝑖
𝑦𝑗
𝑝𝑗
𝐶𝑜𝑣(𝑡𝑖𝑡𝑗)
𝑁
𝑗>𝑖
𝑁
𝑖=1
𝑁
𝑖=1
=
1
𝑛
𝑦𝑖
𝑝𝑖
2
𝑝𝑖 1 − 𝑝𝑖 − 2
𝑦𝑖
𝑝𝑖
𝑦𝑗
𝑝𝑗
𝑝𝑖𝑝𝑗
𝑁
𝑗>𝑖
𝑁
𝑖=1
𝑁
𝑖=1
=
1
𝑛
𝑦𝑖
2
𝑝𝑖
− 𝑌2
𝑁
𝑖=1
=
1
𝑛
𝑝𝑖
𝑦𝑖
𝑝𝑖
− 𝑌
2
𝑁
𝑖=1
(𝑡𝑒𝑟𝑏𝑢𝑘𝑡𝑖)

83. Estimator untuk PPS WR
(Hansen Hurwitz Estimator)
• Unbiased estimator varians untuk total karakteristik:
𝑣 𝑌𝑝𝑝𝑠 =
1
𝑛(𝑛 − 1)
𝑦𝑖
𝑝𝑖
− 𝑌𝑝𝑝𝑠
2
𝑛
𝑖=1
Bukti:
𝑣 𝑌𝑝𝑝𝑠 =
1
𝑛(𝑛 − 1)
𝑦𝑖
𝑝𝑖
− 𝑌𝑝𝑝𝑠
2
𝑛
𝑖=1
𝑛(𝑛 − 1)𝑣 𝑌𝑝𝑝𝑠 =
𝑦𝑖
𝑝𝑖
− 𝑌𝑝𝑝𝑠
2
𝑛
𝑖=1
𝑛 𝑛 − 1 𝐸 𝑣 𝑌𝑝𝑝𝑠 = 𝐸
𝑦𝑖
𝑝𝑖
− 𝑌𝑝𝑝𝑠
2
𝑛
𝑖=1
𝑛 𝑛 − 1 𝐸 𝑣 𝑌𝑝𝑝𝑠 = 𝐸
𝑦𝑖
𝑝𝑖
− 𝑌
2
− 𝑛 𝑌𝑝𝑝𝑠 − 𝑌
2
𝑛
𝑖=1

84. Estimator untuk PPS WR
(Hansen Hurwitz Estimator)
• Unbiased estimator varians untuk total karakteristik:
Bukti (lanjutan):
𝑛 𝑛 − 1 𝐸 𝑣 𝑌𝑝𝑝𝑠 = 𝐸
𝑦𝑖
𝑝𝑖
− 𝑌
2
− 𝑛 𝑌𝑝𝑝𝑠 − 𝑌
2
𝑛
𝑖=1
𝑛 𝑛 − 1 𝐸 𝑣 𝑌𝑝𝑝𝑠 = 𝐸 𝑡𝑖
𝑦𝑖
𝑝𝑖
− 𝑌
2
− 𝑛 𝑌𝑝𝑝𝑠 − 𝑌
2
𝑁
𝑖=1
𝑛 𝑛 − 1 𝐸 𝑣 𝑌𝑝𝑝𝑠 = 𝐸 𝑡𝑖
𝑦𝑖
𝑝𝑖
− 𝑌
2
𝑁
𝑖=1
− 𝑛 ∙ 𝑉 𝑌𝑝𝑝𝑠
𝑛 𝑛 − 1 𝐸 𝑣 𝑌𝑝𝑝𝑠 = 𝑛 𝑝𝑖
𝑦𝑖
𝑝𝑖
− 𝑌
2
𝑛
𝑖=1
− 𝑛 ∙ 𝑉 𝑌𝑝𝑝𝑠
𝑛 𝑛 − 1 𝐸 𝑣 𝑌𝑝𝑝𝑠 = 𝑛(𝑛 − 1) ∙ 𝑉 𝑌𝑝𝑝𝑠
𝐸 𝑣 𝑌𝑝𝑝𝑠 = 𝑉 𝑌 (𝑢𝑛𝑏𝑖𝑎𝑠𝑒𝑑)

85. Latihan 4
• Dari data hipotetik di bawah ini, buktikan secara empirik bahwa
penduga total dan penduga varians dari penarikan sampel PPS WR
adalah unbiased ! (ambil n=2).
Unit 𝑿𝒊 𝒀𝒊
A 6 3
B 12 4
C 15 3

86. Estimator untuk PPS WR
(Hansen Hurwitz Estimator)
• Estimasi total:
Estimasi total berdasarkan unit ke-i:
𝑌𝑖 =
𝑦𝑖
𝑝𝑖
Estimasi total berdasarkan 𝑛 sampel:
𝑌𝑝𝑝𝑠 =
1
𝑛
𝑌𝑖
𝑛
𝑖=1
Estimasi varians sampling:
𝑣 𝑌𝑝𝑝𝑠 =
1
𝑛(𝑛 − 1)
𝑌𝑖 − 𝑌𝑝𝑝𝑠
2
𝑛
𝑖=1
• Estimasi rata-rata:
𝑦𝑝𝑝𝑠 =
𝑌𝑝𝑝𝑠
𝑁
Estimasi varians sampling :
𝑣 𝑦𝑝𝑝𝑠 =
1
𝑁2
𝑣(𝑌𝑝𝑝𝑠)

87. Relative Eficiency PPSWRterhadap SRSWR
• Varians SRS WR: 𝑉 𝑌𝑠𝑟𝑠 =
𝑁2
𝑛
𝑆2
=
𝑁
𝑛
𝑦𝑖
2
− 𝑁𝑌2
𝑁
𝑖=1
Unbiased estimator untuk: 𝑦𝑖
2
adalah
1
𝑛
𝑦𝑖
2
𝑝𝑖
𝑛
𝑖=1
𝑁
𝑖=1 dan
Unbiased estimator untuk: 𝑁𝑌2
adalah 𝑌𝑝𝑝𝑠
2
− 𝑣 𝑌𝑝𝑝𝑠
Dengan demikian, unbiased estimator dari varians SRS WR berdasarkan
sampel PPS WR dapat dinyatakan dengan rumus:
𝑣𝑝𝑝𝑠 𝑌𝑠𝑟𝑠 =
𝑁
𝑛2
𝑦𝑖
2
𝑝𝑖
−
1
𝑛
𝑌𝑝𝑝𝑠
2
− 𝑣 𝑌𝑝𝑝𝑠
𝑛
𝑖=1
=
1
𝑛2
𝑁
𝑦𝑖
2
𝑝𝑖
− 𝑛𝑌𝑝𝑝𝑠
2
𝑛
𝑖=1
+
1
𝑛
𝑣 𝑌𝑝𝑝𝑠
• Relative Eficiency (RE) PPS WR terhadap SRS WR:
𝑅𝐸 =
𝑣 𝑌𝑝𝑝𝑠
𝑣𝑝𝑝𝑠 𝑌𝑠𝑟𝑠
× 100%

88. Latihan 5
• Untuk meneliti total produksi jagung di suatu desa, dilakukan pengambilan sampel
petak ladang secara PPS WR dengan size luas tanam. Jumlah petak ladang yang
ditanami jagung sebanyak 160 petak dengan rata-rata luas tanam per petak adalah
250 𝑚2
. Jumlah sampel yang diambil adalah 12 petak dengan data sebagai berikut:
No 1 2 3 4 5 6 7 8 9 10 11 12
Luas
tanam
𝑚2
214 315 343 165 195 270 406 227 270 255 380 335
Produksi
(kg)
321 378 343 264 351 216 609 454 459 408 912 737
a. Perkirakan total produksi jagung di desa tsb dan rata-rata produksi jagung per
petak beserta standar error, RSE, Relative Efficiency terhadap SRS dan confidence
interval-nya. Beri interpretasi.
b. Perkirakan rata-rata produktivitas ladang per 𝒎𝟐
di desa tsb beserta standar
error, RSE, dan confidence interval-nya. Beri interpretasi.
c. Jika petak ladang yang produktivitasnya kurang dari rata-rata produktivitas ladang
per 𝑚2
di desa tsb dikategorikan sebagai lahan kurang produktif, perkirakan
jumlah petak dan luas tanam yang kurang produktif. Lengkapi dengan nilai
standar error, RSE, dan confidence interval-nya. Beri interpretasi.

89. Latihan 6
• Dari total populasi sebanyak 624 perusahaan
di suatu provinsi dilakukan pengambilan
sampel sebanyak 15 perusahaan secara PPS
WR dengan size jumlah pekerja tahun lalu
kemudian dilakukan pencacahan ke
perusahaan terpilih untuk meneliti
pengeluaran perusahaan untuk pembayaran
upah pekerja. Diketahui jumlah pekerja tahun
lalu di provinsi tersebut adalah 1600 orang.
a. Perkirakan rata-rata pengeluaran
perusahaan untuk pembayaran upah pekerja,
lengkapi dengan standar error, RSE, dan 95%
Confidence Interval-nya !
b. Jika diasumsikan jumlah pekerja pada tahun
survei tidak mengalami perubahan dari
jumlah pekerja tahun lalu, perkirakan rata-
rata upah pekerja di provinsi tsb beserta
standar error, RSE, dan 95% Confidence
Interval-nya !
c. Hitung relative efficiency nya terhadap SRS !
No
Jumlah
Pekerja
tahun lalu
Pengeluaran
untuk upah
pekerja (000 rp)
tahun survei
1 40 75240
2 36 54036
3 64 110016
4 24 63144
5 32 57216
6 20 39180
7 16 30912
8 64 189056
9 48 85584
10 52 141388
11 28 81424
12 36 90216
13 60 127740
14 44 76472
15 20 53980

90. Stratified PPS Sampling
• Populasi sebanyak N dibagi menjadi L strata (𝑁1, 𝑁2, … , 𝑁ℎ, … , 𝑁𝐿),
kemudian dari masing-masing strata dilakukan penarikan sampel secara
PPS.
• Probability selection unit ke-i pada strata ke-h adalah:
𝑝ℎ𝑖 =
𝑋ℎ𝑖
𝑋ℎ
• Fraksi sampling (inclusion probability) unit ke-i strata ke-h adalah:
𝑓ℎ𝑖 = 𝜋ℎ𝑖 = 𝑝ℎ𝑖 ∙ 𝑛ℎ =
𝑋ℎ𝑖
𝑋ℎ
∙ 𝑛ℎ
• Estimasi total karakteristik di strata ke-h:
𝑌ℎ =
𝑦ℎ𝑖
𝜋ℎ𝑖
=
1
𝑛ℎ
𝑦ℎ𝑖
𝑝ℎ𝑖
𝑛ℎ
𝑖=1
𝑛ℎ
𝑖=1
• Estimasi varians total karakteristik di strata ke-h:
𝑣 𝑌ℎ =
1
𝑛ℎ(𝑛ℎ − 1)
𝑦ℎ𝑖
𝑝ℎ𝑖
− 𝑌ℎ
2
𝑛ℎ
𝑖=1

91. Stratified PPS Sampling
• Estimasi total karakteristik populasi:
𝑌 = 𝑌ℎ
𝐿
ℎ=1
=
𝑦ℎ𝑖
𝜋ℎ𝑖
=
1
𝑛ℎ
𝑦ℎ𝑖
𝑝ℎ𝑖
𝑛ℎ
𝑖=1
𝐿
ℎ=1
𝑛ℎ
𝑖=1
𝐿
ℎ=1
• Estimasi varians total karakteristik populasi:
𝑣 𝑌 = 𝑣 𝑌ℎ
𝐿
ℎ=1
=
1
𝑛ℎ(𝑛ℎ − 1)
𝑦ℎ𝑖
𝑝ℎ𝑖
− 𝑌ℎ
2
𝑛ℎ
𝑖=1
𝐿
ℎ=1
• Estimasi rata-rata karakteristik populasi:
𝑦 =
𝑌
𝑁
• Estimasi varians rata-rata karakteristik populasi:
𝑣 𝑦 =
1
𝑁2
𝑣(𝑌)

92. Latihan 7
• Populasi sebanyak 40 perusahaan di kota X dibagi menjadi 2 strata, yaitu
industri mikro (strata 1) dan industri kecil (strata 2). Kemudian dari tiap
strata dilakukan penarikan sampel secara PPS WR dengan size jumlah
tenaga kerja. Data yang diperoleh:
Ket: Output dalam juta rupiah
Perkirakan total output perusahaan di kota X beserta standar error , rse,
dan 95% Confidence Interval-nya !
Strata
Jumlah
perusahaan
Jumlah
pekerja
Sampel
1 25 160
Pekerja 5 4 3 4 2 6
Output 20 18 12 16 6 18
2 15 240
Pekerja 15 20 25 16 18
Output 90 96 120 72 117

93. PPS WOR
• Pada prinsipnya, PPS WOR akan menghasilkan estimator
yang lebih efisien daripada PPS WR.
• Hal ini dikarenakan effective sample size dari PPS WOR akan
lebih besar daripada effective sample size dari PPS WR.
• Namun, PPS WOR memerlukan prosedur yang kompleks
sehingga kadangkala sulit diterapkan pada survei skala
besar.
• Pada survei skala besar, fraksi sampling biasanya kecil
sehingga efisiensi dari PPS WOR dan PPS WR perbedaannya
tidak terlalu signifikan.
• Jika fraksi sampling besar, lebih baik menggunakan PPS
WOR

94. Des Raj’s Ordered Estimator
• Jika sampel sebanyak n unit (𝑦𝑖, 𝑦2, … , 𝑦𝑛) diambil secara
PPS WOR dari populasi sebanyak N unit, maka:
𝑧𝑖 = 𝑦𝑘 + 1 − 𝑝𝑘
𝑖−1
𝑘=1
𝑦𝑖
𝑝𝑖
𝑖−1
𝑘=1
, 𝑖 = 2,3, … , 𝑛
• Estimator total karakteristiknya:
𝑌𝐷 =
1
𝑛
𝑧𝑖
𝑛
𝑖=1
• Estimator varians total karakteristiknya:
𝑣 𝑌𝐷 =
1
𝑛(𝑛 − 1)
𝑧𝑖 − 𝑌𝐷
2
𝑛
𝑖=1

95. Latihan 8
• Sampel berukuran 3 diambil dari populasi sebanyak 10 unit
secara PPS WOR. Jika total size adalah 100 dan data yang
diperoleh sebagai berikut:
Perkirakan total karakteristik populasi dengan Des Raj’s
Ordered Estimator beserta standar error dan rse-nya !
No 1 2 3
𝑥𝑖 6 20 10
𝑦𝑖 3 10 7

96. Horvitz Thompson Estimator (HT)
• Horvitz Thompson Estimator adalah general estimator untuk
estimasi total karakteristik populasi yang dapat digunakan
untuk berbagai desain sampling, baik WR maupun WOR.
• Sebuah sampel sebanyak n unit diambil secara PPS, dan:
𝜋𝑖 menyatakan peluang unit ke-i masuk dalam sampel
𝜋𝑖𝑗 menyatakan peluang unit ke-i dan unit ke-j keduanya
masuk dalam sampel

97. Horvitz Thompson Estimator (HT)
• Jika penarikan sampel dilakukan dengan PPS WR, nilai 𝜋𝑖
dan 𝜋𝑖𝑗 diperoleh dari persamaan:
𝜋𝑖 = 𝑃(𝑢𝑛𝑖𝑡 𝑖 𝑚𝑎𝑠𝑢𝑘 𝑑𝑎𝑙𝑎𝑚 𝑠𝑎𝑚𝑝𝑒𝑙)
𝜋𝑖 = 1 − 𝑃(𝑢𝑛𝑖𝑡 𝑖 𝑡𝑖𝑑𝑎𝑘 𝑚𝑎𝑠𝑢𝑘 𝑑𝑎𝑙𝑎𝑚 𝑠𝑎𝑚𝑝𝑒𝑙)
𝝅𝒊 = 𝟏 − 𝟏 − 𝒑𝒊
𝒏
𝝅𝒊𝒋 = 𝝅𝒊 + 𝝅𝒋 − 𝟏 − 𝟏 − 𝒑𝒊 − 𝒑𝒋
𝒏

98. Horvitz Thompson Estimator (HT)
• Jika penarikan sampel dilakukan dengan PPS WOR (n=2),
nilai 𝜋𝑖 dan 𝜋𝑖𝑗 diperoleh dari persamaan:
𝜋𝑖 = 𝑝𝑖 +
𝑝𝑗𝑝𝑖
(1 − 𝑝𝑗)
= 𝑝𝑖 1 +
𝑝𝑗
(1 − 𝑝𝑗)
𝑁
𝑗≠𝑖
𝑁
𝑗≠𝑖
= 𝒑𝒊 𝟏 + 𝑨 −
𝒑𝒊
𝟏 − 𝒑𝒊
𝜋𝑖𝑗 =
𝑝𝑖𝑝𝑗
(1 − 𝑝𝑖)
+
𝑝𝑗𝑝𝑖
(1 − 𝑝𝑗)
= 𝒑𝒊𝒑𝒋
𝟏
(𝟏 − 𝒑𝒊)
+
𝟏
(𝟏 − 𝒑𝒋)
Keterangan:
𝑨 =
𝒑𝒊
𝟏 − 𝒑𝒊
𝑵
𝒊=𝟏

99. Horvitz Thompson Estimator (HT)
• Estimator total karakteristik:
𝑌𝐻𝑇 =
𝑦𝑖
𝜋𝑖
𝑣
𝑖=1
• Estimasi varians total karakteristik:
𝑣 𝑌𝐻𝑇 =
1
𝜋𝑖
2
−
1
𝜋𝑖
𝑦𝑖
2
+ 2
1
𝜋𝑖𝜋𝑗
−
1
𝜋𝑖𝑗
𝑗>𝑖
𝑣
𝑖=1
𝑣
𝑖=1
𝑦𝑖𝑦𝑗
Keterangan:
𝑣 : effective sample size (jumlah unit yang berbeda dalam
sampel)

100. Contoh:
• Dari area sawah seluas 100 ℎ𝑎 dibagi menjadi beberapa
sub-area, dan diambil 4 sub-area sebagai sampel secara PPS
WR (proporsional terhadap luas sub-area)untuk meneliti
produksi padi di area tersebut. Sub-area A terpilih 2 kali.
Data yang diperoleh:
No urut
sampel
No urut
effective
sample size
(i)
Sub-Area 𝒙𝒊 𝒚𝒊
1
1
A 5 60
2 A 5 60
3 2 G 2 14
4 3 K 1 1

101. • Hitung selection probability (𝑝𝑖)
𝑝1 =
𝑥1
𝑋
=
5
100
= 0,05
𝑝2 =
𝑥2
𝑋
=
2
100
= 0,02
𝑝3 =
𝑥3
𝑋
=
1
100
= 0,01
• Hitung inclusion probability 𝜋𝑖
𝜋𝑖 = 1 − (1 − 𝑝𝑖)𝑛
𝜋1 = 1 − 1 − 0,05 4 = 0.1855
𝜋2 = 1 − 1 − 0,02 4 = 0.0776
𝜋3 = 1 − 1 − 0,01 4 = 0.0394

102. Hitung Joint Inclusion Probability 𝝅𝒊𝒋
• Rumus:
𝜋𝑖𝑗 = 𝜋𝑖 + 𝜋𝑗 − 1 − 1 − 𝑝𝑖 − 𝑝𝑗
𝑛
𝜋12 = 𝜋1 + 𝜋2 − 1 − 1 − 𝑝1 − 𝑝2
4
= 0,1855 + 0,0776 − 1 − 1 − 0,05 − 0,02 4
= 0,0112
𝜋13 = 𝜋1 + 𝜋3 − 1 − 1 − 𝑝1 − 𝑝3
4
= 0,1855 + 0,0394 − 1 − 1 − 0,05 − 0,01 4
= 0,0056
𝜋23 = 𝜋2 + 𝜋3 − 1 − 1 − 𝑝2 − 𝑝3
4
= 0,0776 + 0,0394 − 1 − 1 − 0,02 − 0,01 4
= 0,0023

103. Hitung estimasi total
• Estimasi total:
𝑌𝐻𝑇 =
𝑦𝑖
𝜋𝑖
=
60
0,1855
+
14
0,0776
+
1
0,0394
= 529
𝑣
𝑖=1
• Estimasi varians:
𝑣 𝑌𝐻𝑇 =
1
𝜋𝑖
2
−
1
𝜋𝑖
𝑦𝑖
2
+ 2
1
𝜋𝑖𝜋𝑗
−
1
𝜋𝑖𝑗
𝑗>𝑖
𝑣
𝑖=1
𝑣
𝑖=1
𝑦𝑖𝑦𝑗
=
1
0,18552
−
1
0,1855
602
+
1
0,07762
−
1
0,0776
142
+
1
0,03942
−
1
0,0394
12
+ 2
1
0,1855 ∙ 0,0776
−
1
0,0112
60 14
+2
1
0,1855 ∙ 0,0394
−
1
0,0056
60 1 + 2
1
0,0776 ∙ 0,0394
−
1
0,0023
14 1
= 74.538
𝑠𝑒 𝑌𝐻𝑇 = 𝑣 𝑌𝐻𝑇 = 273

104. Latihan 9
• Sampel berukuran 2 diambil dari populasi sebanyak 5 unit
secara PPS. Data populasi sebagai berikut:
Jika unit ke-2 dan ke-5 terpilih sebagai sampel, perkirakan
total karakteristik populasi dengan Horvitz Thompson
Estimator beserta standar error dan rse-nya:
a. Jika sampel tersebut diambil secara PPS WR
b. Jika sampel tersebut diambil secara PPS WOR
No 1 2 3 4 5
𝑥𝑖 6 20 10 5 9
𝑦𝑖 - 10 - - 6

105. Unordered Murthy’s Method
• Dalam PPS WOR, jika unit yang terpilih pertama mempunyai
probability selection 𝑝𝑖, maka
probability selection untuk terpilihnya unit sampel yang kedua
adalah
𝑝𝑗
1 − 𝑝𝑖
probability selection untuk terpilihnya unit sampel yang ketiga
adalah
𝑝𝑘
1 − 𝑝𝑖 − 𝑝𝑗
probability selection untuk terpilihnya unit sampel yang
keempat adalah
𝑝𝑙
1 − 𝑝𝑖 − 𝑝𝑗 − 𝑝𝑘
dst

106. Unordered Murthy’s Method
• Estimator total:
𝑌𝑀 =
𝑃 𝑠|𝑖 𝑦𝑖
𝑛
𝑖=1
𝑃(𝑠)
𝑃 𝑠|𝑖 : conditional probability untuk mendapatkan suatu set sampel
jika unit ke-i terpilih sebagai sampel pertama
𝑃(𝑠) : unconditional probability untuk mendapatkan suatu set
sampel
𝑦𝑖 : nilai karakteristik untuk unit ke-i
• Estimasi varians total:
𝑣 𝑌𝑀 =
1
𝑃(𝑠) 2
𝑃 𝑠 𝑃 𝑠 𝑖𝑗 − 𝑃 𝑠 𝑖 𝑃(𝑠|𝑗) 𝑝𝑖𝑝𝑗
𝑦𝑖
𝑝𝑖
−
𝑦𝑗
𝑝𝑗
2
𝑛
𝑗>𝑖
𝑛
𝑖=1
𝑃 𝑠|𝑖𝑗 : conditional probability untuk mendapatkan suatu set sampel jika unit
ke-i terpilih sebagai sampel pertama dan unit ke-j terpilih sebagai sampel kedua

107. Unordered Murthy’s Method
• Untuk n=2 (sampel terdiri dari unit ke-i dan ke-j):
𝑃 𝑠|𝑖 =
𝑝𝑗
1 − 𝑝𝑖
𝑃 𝑠|𝑗 =
𝑝𝑖
1 − 𝑝𝑗
𝑃 𝑠 = 𝑝𝑖 ∙ 𝑃 𝑠 𝑖 + 𝑝𝑗 ∙ 𝑃 𝑠 𝑗 =
𝑝𝑖𝑝𝑗(2 − 𝑝𝑖 − 𝑝𝑗)
(1 − 𝑝𝑖)(1 − 𝑝𝑗)
Estimator total:
𝒀𝑴 =
𝟏
𝟐 − 𝒑𝒊 − 𝒑𝒋
𝟏 − 𝒑𝒋
𝒚𝒊
𝒑𝒊
+ (𝟏 − 𝒑𝒊)
𝒚𝒋
𝒑𝒋
Varians sampling:
𝒗 𝒀𝑴 =
(𝟏 − 𝒑𝒊)(𝟏 − 𝒑𝒋)(𝟏 − 𝒑𝒊 − 𝒑𝒋)
𝟐 − 𝒑𝒊 − 𝒑𝒋
𝟐
𝒚𝒊
𝒑𝒊
−
𝒚𝒋
𝒑𝒋
𝟐

108. Latihan 10
• Sampel berukuran 2 diambil dari populasi sebanyak 5 unit
secara PPS WOR. Data yang populasi sebagai berikut:
Jika unit ke-2 dan ke-5 terpilih sebagai sampel, perkirakan
total karakteristik populasi dengan Murthy’s Estimator
beserta standar error dan rse-nya !
No 1 2 3 4 5
𝑥𝑖 6 20 10 5 9
𝑦𝑖 - 10 - - 6

109. Rao, Hartley, Cochran Estimator (RHC)
• Estimator ini digunakan jika pengambilan sampel dilakukan dengan
random group method.
• Dalam random group method, populasi sebanyak N dibagi menjadi n
group secara random, kemudian dari masing-masing group diambil satu
unit sebagai sampel
• Dengan demikian, akan terdapat sampel sebanyak n unit.

110. Rao, Hartley, Cochran Estimator (RHC)
• Misalkan 𝑥𝑔 menyatakan nilai variabel pendukung untuk unit yang
terpilih sampel pada strata ke-g, dan 𝑋𝑔 menyatakan total nilai variabel
pendukung untuk strata ke-g, maka estimator totalnya:
𝑌𝑅𝐻𝐶 = 𝑋𝑔
𝑦𝑔
𝑥𝑔
𝑛
𝑔=1
• Estimasi variansnya:
𝑣 𝑌𝑅𝐻𝐶 =
𝑁𝑔
2
− 𝑁
𝑛
𝑔=1
𝑁2 − 𝑁𝑔
2
𝑛
𝑔=1
𝑋𝑔
𝑦𝑔
𝑥𝑔
− 𝑌𝑅𝐻𝐶
2
𝑛
𝑔=1

111. Latihan 11
• Untuk memperkirakan banyaknya tangkapan ikan di kabupaten A,
dilakukan pengambilan sampel secara PPS WOR Random group method
dengan size jumlah perahu yang datang di tempat pelelangan ikan (TPI).
Jumlah populasi TPI sebanyak 12 dan diambil 4 TPI sebagai sampel. Data
yang diperoleh:
Perkirakan total tangkapan ikan di Kabupaten A beserta standar error dan
rse-nya !
Group Nama TPI
Jumlah
perahu
Sampel terpilih
Nama
TPI
Jumlah
Perahu
Jumlah
ikan
(kwintall)
1 A, G, L 16 G 8 12
2 B, E, I 20 B 10 16
3 C, H, J 10 H 4 8
4 D, F, K 24 K 8 10

112. TERIMA KASIH
Have A Nice Sampling

113. RATIO ESTIMATOR
Oleh: Adhi Kurniawan
METODE PENARIKAN SAMPEL

114. Deskripsi
• Selain variabel yang diteliti 𝑦 , satu atau lebih variabel pendukung 𝑥 bisa dikaji
korelasinya dari setiap unit populasi.
• Pada tahap estimasi, korelasi antara variabel yang diteliti 𝑦 dan variabel pendukung
𝑥 bisa digunakan untuk menghasilkan estimasi-estimasi yang lebih tepat daripada
yang diperoleh dari variabel 𝑦 itu sendiri.
• Salah satu metode estimasi yang dipakai untuk menghubungkan variabel 𝑦 dan 𝑥
adalah dengan menggunakan rasio 𝑅 = 𝑟 =
𝑦
𝑥
dari dua rata-rata sampel 𝑦 dan 𝑥 .
• Rasio ini digunakan sebagai estimator dari rasio rata-rata variabel 𝑦 dan 𝑥 dalam
populasi 𝑅 =
𝑌
𝑋
• Rasio ini juga dapat digunakan untuk memperoleh suatu estimasi tentang total populasi
yang lebih akurat daripada estimasi yang ditentukan dengan perkalian sederhana
antara total karakteristik sampel (𝑦) dengan invers dari fraksi sampling.

115. Definisi
Ratio estimator adalah suatu metode estimasi yang
memanfaatkan perbandingan/rasio antara variabel yang
diteliti (𝑦) dengan variabel bantu/pendukung 𝑥 untuk
meningkatkan efisiensi pendugaan parameter populasi.

116. Mengapa menggunakan Estimasi Rasio ? (1)
1. Seringkali kita ingin melakukan estimasi rasio suatu
variabel terhadap variabel lainnya.
Misalkan:
Estimasi rasio produksi padi terhadap luas lahan
Estimasi rasio penduduk laki-laki terhadap penduduk
perempuan
Estimasi pendapatan per kapita
Estimasi rasio hutang terhadap asset perusahaan

117. Mengapa menggunakan Estimasi Rasio ? (2)
2. Kadang kala kita ingin melakukan estimasi total, namun ukuran
populasi (N) tidak diketahui
Kita tidak dapat menggunakan rumus 𝑌 = 𝑁𝑦 seperti yang telah
dipelajari sebelumnya. Namun, kita mempunyai nilai total
karakteristik untuk variabel lain, misalkan 𝑋. Dengan demikian,
ukuran populasi bisa diestimasi dengan rumus:
𝑁 =
𝑋
𝑥
Dan estimasi total karakteristik untuk variabel yang diteliti (y) adalah:
𝑌 =
𝑋
𝑥
𝑦

118. Mengapa menggunakan Estimasi Rasio ? (3)
3. Estimasi rasio seringkali digunakan untuk meningkatkan presisi dari
estimasi rata-rata dan estimasi total
Contoh:
Laplace ingin melakukan estimasi total penduduk Prancis. Dia bisa
mendapatkan estimasi total penduduk dengan mengalikan rata-rata jumlah
penduduk 𝑦 di 30 komunitas dengan jumlah komunitas di Prancis (𝑁).
Namun, dia menggunakan informasi lain yaitu jumlah catatan kelahiran (𝑥)
untuk meningkatkan presisi.
Dia beralasan bahwa jumlah kelahiran akan sebanding dengan jumlah
penduduk. Wilayah yang penduduknya banyak, jumlah kelahirannya juga
banyak, sehingga korelasi antara kedua variabel tersebut positif.

119. Mengapa menggunakan Estimasi Rasio ? (4)
4. Estimasi rasio bisa digunakan untuk melakukan adjustment dari data
sampel sehingga akan diperoleh estimasi total yang lebih akurat.
Contoh:
 Sampel SRS sebanyak n=400 mahasiswa (240 wanita, 160 pria)
diambil dari populasi sebanyak N=4000 mahasiswa di sebuah
universitas.
 Dari data sampel diketahui bahwa sebanyak 84 wanita dan 40 pria
ingin berkarir di bidang riset.
 Dengan menggunakan informasi hanya dari SRS, maka estimasi
total mahasiswa yang ingin berkarir di bidang riset adalah:
𝑌 =
4000
400
× 124 = 1240

120. Mengapa menggunakan Estimasi Rasio ? (4)
Jika diketahui bahwa jumlah populasi mahasiswa wanita adalah 2700 orang
dan populasi mahasiswa pria adalah 1300 orang maka estimasi yang lebih
akurat mengenai total mahasiswa yang ingin berkarir di bidang riset adalah:
𝑌 =
84
240
× 2700 +
40
160
× 1300 = 1270
Pada kasus di atas, estimasi rasio digunakan berdasarkan jenis kelamin.
Berdasarkan data sampel 60% mahasiswa adalah wanita, tetapi dari data
populasi diketahui bahwa persentase mahasiswa perempuan adalah 67,5%,
Dengan informasi ini kita bisa melakukan adjustment terhadap estimasi total
mahasiswa yang ingin berkarir di bidang riset.
Penggunaan estimasi rasio dalam kasus ini disebut poststratification.

121. Mengapa menggunakan Estimasi Rasio ? (5)
5. Estimasi rasio bisa digunakan untuk adjustment nonrespon.
Contoh:
 Untuk meneliti jumlah upah yang dikeluarkan perusahaan, diambil
beberapa perusahaan sebagai sampel.
 Misalkan 𝑦𝑖 adalah jumlah upah yang dikeluarkan oleh perusahaan ke-i,
dan 𝑥𝑖 adalah jumlah karyawan di perusahaan ke-i dan jumlah karyawan
untuk semua perusahaan dalam populasi (𝑋) diketahui.
 Kita juga mengasumsikan bahwa jumlah upah yang dikeluarkan
perusahaan akan berhubungan erat dengan jumlah karyawan.
 Misalkan, ada beberapa perusahaan yang nonrespon.
 Adjustment estimasi total upah dengan mengalikan rasio upah terhadap
pekerja dari data sampel 𝑦/𝑥 dengan total pekerja 𝑋 :
𝑌 =
𝑦
𝑥
𝑋

122. Ratio Estimator
Ratio estimator dibedakan menjadi 3 kondisi:
a. Rasio berupa karakteristik yang sama atau berhubungan dengan
periode sebelumnya.
 𝑋 adalah jenis karakteristik yang sama dengan 𝑌 tetapi berasal
dari periode sebelumnya.
Contoh:
Suatu survei rumahtangga yang dilakukan tahun 2012 menggunakan
hasil Sensus Penduduk 2010 sebagai dasar rasio dan menggunakan
blok sensus sebagai unit sampling.
𝑦 adalah jumlah rumahtangga hasil updating tahun 2012 dari blok
sensus terpilih.
𝑥 adalah jumlah rumahtangga hasil Sensus Penduduk 2010 dari blok
sensus terpilih.
Dengan demikian 𝑅 =
𝑦
𝑥
merupakan perubahan banyaknya
rumahtangga saat survei dibandingkan saat sensus.

123. Ratio Estimator
b. Rasio dari dua karakteristik berbeda yang berkorelasi kuat pada
periode yang sama.
 𝑋 dan 𝑌 merupakan dua buah karakteristik berbeda yang berasal
dari periode yang sama dan diketahui berkorelasi positif.
Contoh:
Dari Survei Konsumsi/Pengeluaran rumah tangga diperoleh:
𝑦 adalah total konsumsi beras dari rumah tangga sampel
𝑥 adalah total anggota rumah tangga (ART) dari rumah tangga sampel
Dengan demikian 𝑅 =
𝑦
𝑥
merupakan konsumsi beras per kapita

124. Ratio Estimator
c. Modifikasi lain dalam penggunaan estimasi rasio adalah menggunakan
sumber lain dan data sampel untuk variabel yang sama sebagai faktor
pengali.
Contoh:
Misalkan, telah ditentukan data proyeksi penduduk merupakan data yang
disepakati untuk berbagai perencanaan dan kajian, maka dengan estimator
rasio, berarti faktor pengali dari survei adalah:
𝐹 = 𝑅 =
𝑦
𝑥
𝑦 adalah jumlah penduduk pada tahun tertentu dari hasil proyeksi penduduk
𝑥 adalah jumlah penduduk sampel

125. Sifat-sifat Ratio Estimator
• Secara umum, ratio estimator adalah estimator yang bias
konsisten. Maksudnya, semakin besar ukuran sampel maka
biasnya akan semakin kecil.
• Ratio estimator akan bersifat best linear unbiased estimator
jika memenuhi 2 kondisi:
a. Hubungan (korelasi) antara 𝑦𝑖 dan 𝑥𝑖 berupa garis lurus
(linear), positif, dan melalui titik origin (0,0)
b. Varians 𝑦𝑖 pada garis lurus bersifat proportional terhadap
𝑥𝑖

126. Sifat-sifat Ratio Estimator
• Jika jumlah sampel (𝑛) besar, limiting distribution dari ratio estimate akan
mengikuti distribusi normal.
• Jika jumlah sampel (𝑛) moderate, ratio estimate mempunyai
kecenderungan mengikuti positive skewness distribution.
• Dalam penghitungan bias, terdapat rumus untuk berbagai ukuran sampel,
tetapi perkiraan varians hanya berlaku untuk jumlah sampel berukuran
besar
• Sebagai aturan praktis, Cochran menyatakan bahwa pendekatan large-
sample untuk penghitungan varians dapat digunakan jika:
a. Ukuran sampel lebih dari 30
b. Koefisien variasi (CV) dari variabel x dan variabel y, keduanya kurang
dari 10%

127. Notasi
𝑦𝑖 : nilai karakteristik yang diteliti dari unit sampel ke-i
𝑥𝑖 : nilai variabel pendukung dari unit sampel ke-i
𝑦 : total nilai karakteristik yang diteliti dari data sampel
𝑦 = 𝑦𝑖
𝑛
𝑖=1
𝑥 : total nilai variabel pendukung dari data sampel
𝑥 = 𝑥𝑖
𝑛
𝑖=1
𝑌 : total nilai karakteristik yang diteliti untuk populasi
𝑌 = 𝑦𝑖
𝑁
𝑖=1
𝑋 : total nilai variabel pendukung untuk populasi
𝑋 = 𝑥𝑖
𝑁
𝑖=1

128. Estimator
Jika penarikan sampel dilakukan secara simple random
sampling, dan nilai karakteristik 𝒚 dan 𝒙 tersedia untuk
setiap unit dalam sampel dengan nilai populasi 𝑿
diketahui, maka:
• Estimator rasio
𝑅 =
𝑦
𝑥
• Estimator rata-rata
𝑦𝑅 = 𝑅𝑋
• Estimator total
𝑌𝑅 = 𝑅𝑋

129. Estimasi varians
• Varians rata-rata:
𝑣 𝑦𝑅 =
1 − 𝑓
𝑛(𝑛 − 1)
𝑦𝑖 − 𝑅𝑥𝑖
2
𝑛
𝑖=1
Rumus di atas dapat dijabarkan menjadi:
𝑣 𝑦𝑅 =
1 − 𝑓
𝑛(𝑛 − 1)
𝑦𝑖
2
− 2𝑅 𝑦𝑖𝑥𝑖
𝑛
𝑖=1
+ 𝑅2 𝑥𝑖
2
𝑛
𝑖=1
𝑛
𝑖=1
=
1 − 𝑓
𝑛
𝑠𝑦
2 − 2𝑅𝑠𝑦𝑥 + 𝑅2𝑠𝑥
2
Keterangan:
𝑠𝑦𝑥 =
1
𝑛 − 1
𝑦𝑖 − 𝑦 𝑥𝑖 − 𝑥 → 𝑠𝑎𝑚𝑝𝑙𝑒 𝑐𝑜𝑣𝑎𝑟𝑖𝑎𝑛𝑐𝑒
𝑛
𝑖=1

130. Bukti:
𝑣 𝑦𝑅 =
1 − 𝑓
𝑛(𝑛 − 1)
𝑦𝑖 − 𝑅𝑥𝑖
2
𝑛
𝑖=1
Rumus di atas dapat dijabarkan menjadi:
𝑣 𝑦𝑅 =
1 − 𝑓
𝑛(𝑛 − 1)
𝑦𝑖 − 𝑦 + 𝑦 − 𝑅𝑥𝑖
2
𝑛
𝑖=1
=
1 − 𝑓
𝑛(𝑛 − 1)
𝑦𝑖 − 𝑦 2
+ 2 𝑦𝑖 − 𝑦 𝑦 − 𝑅𝑥𝑖 + 𝑦 − 𝑅𝑥𝑖
2
𝑛
𝑖=1
=
1 − 𝑓
𝑛(𝑛 − 1)
𝑦𝑖 − 𝑦 2
+ 2𝑅 𝑦𝑖 − 𝑦 𝑥 − 𝑥𝑖 + 𝑅2
𝑥 − 𝑥𝑖
2
𝑛
𝑖=1
=
1 − 𝑓
𝑛(𝑛 − 1)
𝑦𝑖 − 𝑦 2
− 2𝑅 𝑦𝑖 − 𝑦 𝑥𝑖 − 𝑥 + 𝑅2
𝑥𝑖 − 𝑥 2
𝑛
𝑖=1
=
1 − 𝑓
𝑛
1
𝑛 − 1
𝑦𝑖 − 𝑦 2
𝑛
𝑖=1
− 2𝑅
1
𝑛 − 1
𝑦𝑖 − 𝑦 𝑥𝑖 − 𝑥
𝑛
𝑖=1
+
1
𝑛 − 1
𝑥𝑖 − 𝑥 2
𝑛
𝑖=1
𝑣 𝑦𝑅 =
1 − 𝑓
𝑛
𝑠𝑦
2
− 2𝑅𝑠𝑦𝑥 + 𝑅2
𝑠𝑥
2
=
(1 − 𝑓)
𝑛
𝑠𝑦
2
− 2𝑅𝜌𝑠𝑦𝑠𝑥 + 𝑅2
𝑠𝑥
2

131. Estimasi varians
• Varians rasio:
𝑣 𝑅 =
𝑣(𝑦𝑅)
𝑋2
=
1 − 𝑓
𝑛𝑋2
𝑠𝑦
2 − 2𝑅𝑠𝑦𝑥 + 𝑅2𝑠𝑥
2
• Varians total:
𝑣 𝑌𝑅 = 𝑁2𝑣 𝑦𝑅
=
𝑁2
(1 − 𝑓)
𝑛
𝑠𝑦
2
− 2𝑅𝑠𝑦𝑥 + 𝑅2
𝑠𝑥
2

132. Latihan 1
• Berikut ini adalah data sampel dari 30 perusahaan yang diambil secara SRS WOR dari
325 perusahaan di Kota A. x menyatakan jumlah pekerja dan y adalah jumlah pekerja
yang absen. Diketahui jumlah pekerja di kota A 25000 orang.
a. Perkirakan persentase pekerja yang absen beserta standar error ,rse dan 95%CI-nya !
b. Perkirakan rata-rata pekerja yang absen per perusahaan beserta standar error , rse,
dan 95%CI-nya !
c. Perkirakan total pekerja yang absen di Kota A beserta standar error dan rse, dan
95%CI-nya
No x y No x y No x y No x y No x y
1 95 9 7 125 9 13 57 5 19 103 9 25 63 5
2 79 7 8 81 10 14 132 13 20 52 8 26 83 7
3 30 3 9 43 6 15 47 4 21 67 14 27 124 13
4 45 2 10 53 2 16 43 9 22 64 6 28 31 2
5 28 3 11 148 16 17 116 12 23 75 6 29 96 23
6 142 8 12 89 4 18 65 8 24 69 8 30 42 13

133. Latihan 2
• Dari data Sensus Ternak tahun lalu diperoleh informasi bahwa jumlah peternak sapi di suatu
wilayah sebanyak 75.308 rumah tangga peternak dan rata-rata jumlah sapi untuk tiap peternak
sebanyak 12 ekor. Sebuah sampel acak sederhana sebanyak 2.055 peternak diambil dari
populasi tersebut untuk memperkirakan produksi susu yang dihasilkan. Jumlah sapi yang
diperoleh dari hasil observasi adalah 25.071 ekor dan rata-rata produksi susu untuk tiap
peternak sebanyak 300 liter per hari. Informasi lain yang diperoleh sebagai berikut:
𝑠𝑦 = 29,4
𝑠𝑥 = 0,96
𝜌 = 0,825
Dengan menggunakan ratio estimator,
a. Perkirakan rata-rata produksi susu per hari yang dihasilkan oleh satu ekor sapi beserta
standar error, rse, dan 95% Confidence Interval-nya !
b. Perkirakan rata-rata produksi susu per hari yang dihasilkan oleh rumah tangga peternak
beserta standar error, rse, dan 95% Confidence Interval-nya !
c. Perkirakan total produksi susu per hari di wilayah tersebut beserta standar error, rse, dan
95% Confidence Interval-nya !

134. BIAS PADA RATIO ESTIMATOR
• Tidak seperti estimator 𝑦 dan 𝑌 pada SRS, ratio estimator
merupakan estimator yang bias dalam menduga nilai 𝑌𝑅 dan
𝑌𝑅.
• Bias pada ratio estimator disebabkan karena 𝑦 kita kalikan
dengan
𝑋
𝑥
sehingga 𝐸 𝑦𝑅 ≠ 𝑌𝑅.
• Misalkan:
𝑌𝑅 =
𝑌
𝑋
∙ 𝑋 = 𝑌 1 −
𝑋 − 𝑋
𝑋
Maka
𝑌𝑅 − 𝑌 =
𝑌
𝑋
∙ 𝑋 − 𝑌 = 𝑌 1 −
𝑋 − 𝑋
𝑋
− 𝑌

135. BIAS PADA RATIO ESTIMATOR
Karena 𝐸 𝑌 = 𝑌, maka:
𝐸 𝑌𝑅 − 𝑌 = 𝐸 𝑌 − 𝑌 − 𝐸
𝑌
𝑋
𝑋 − 𝑋
= −𝐸 𝑅 𝑋 − 𝑋
= −𝑐𝑜𝑣 𝑅, 𝑋
𝐸 𝑅 − 𝑅 =
𝐸 𝑌𝑅 − 𝑌
𝑋
=
−𝑐𝑜𝑣(𝑅, 𝑥)
𝑋
𝐵𝑖𝑎𝑠 𝑅
𝑣 𝑅
1/2
=
𝜌 𝑅,𝑥
𝑋
∙
𝑣 𝑅 ∙ 𝑣 𝑥
𝑣 𝑅
1
2
≤
𝑣 𝑥
1
2
𝑋
= 𝐶𝑉 𝑥

136. BIAS PADA RATIO ESTIMATOR
Pada desain SRS:
𝐸 𝑅 − 𝑅 ≈ 1 −
𝑛
𝑁
1
𝑛𝑋2
𝑅𝑠𝑥
2 − 𝜌(𝑥,𝑦)𝑠𝑥𝑠𝑦
=
1
𝑋2
𝑅 𝑣 𝑥 − 𝑐𝑜𝑣 𝑥, 𝑦
Kesimpulan:
Bias dari 𝑅 akan kecil jika:
1) Sample size (𝑛) besar
2) Fraksi sampling
𝑛
𝑁
besar
3) 𝑋 besar
4) 𝑠𝑥 kecil
5) Correlation coefficient antara x dan y 𝜌(𝑥,𝑦) mendekati 1

137. MSE PADA RATIO ESTIMATOR
𝑀𝑆𝐸 𝑅 = 𝐸 𝑅 − 𝑅
2
= 𝐸
𝑦 − 𝑅𝑥
𝑥
2
= 𝐸
𝑦 − 𝑅𝑥
𝑋
1 −
𝑥 − 𝑋
𝑥
2
= 𝐸
𝑦 − 𝑅𝑥
𝑋
2
+
𝑦 − 𝑅𝑥
𝑋
2
𝑥 − 𝑋
𝑥
2
− 2
𝑥 − 𝑋
𝑥
Dengan asumsi 𝑥 ≈ 𝑋 maka:
𝐸
𝑦 − 𝑅𝑥
𝑥
2
≈ 𝐸
𝑦 − 𝑅𝑥
𝑋
2
=
1
𝑋2
𝐸 𝑦 − 𝑅𝑥 2

138. MSE PADA RATIO ESTIMATOR
𝑀𝑆𝐸 𝑅 =
1
𝑋2
𝐸 𝑦 − 𝑅𝑥 2
Untuk desain SRS:
𝑀𝑆𝐸 𝑅 = 1 −
𝑛
𝑁
1
𝑛𝑋2
𝑠𝑦
2 − 2𝑅 𝜌(𝑥,𝑦) 𝑠𝑥𝑠𝑦 + 𝑅2𝑠𝑥
2
Kesimpulan:
MSE akan kecil jika:
1) Ukuran sampel n besar
2) Fraksi sampling besar
3) Deviasi di sekitar garis 𝑦 = 𝑅𝑥 kecil
4) Koefisien korelasi 𝜌(𝑥,𝑦) mendekati 1
5) Nilai X besar

139. POPULASIKECILYANGMENGILUSTRASIKANBIAS
• Bias dan MSE dari ratio estimator pada desain SRS bisa
diilustrasikan dengan membayangkan sampel yang diambil
dari suatu populasi yang sangat kecil dan melihat sample
space, yaitu sekumpulan dari all possible samples.
• Misalkan kita ingin mengestimasi jumlah total dari ikan yang
ditangkap pada suatu lokasi penangkapan.
• Misalkan N=4 lokasi sepanjang sungai dan jumlah jaring 𝑥𝑖
pada setiap lokasi dalam populasi.
i Lokasi 1 2 3 4
𝑥𝑖 Jumlah Jaring 4 5 8 5
𝑦𝑖 Jumlah Ikan 200 300 500 400

140. • Total populasi sebenarnya adalah1400 ikan.
• Total populasi untuk variabel tambahan adalah 22 jaring
• Simple random sample sebanyak n=2 lokasi dipilih dan
estimasi rasio digunakan untuk mengestimasi total jumlah
ikan yang ditangkap.
• Misalkan sampel terpilih adalah 𝑆 = 1,2 yang terdiri dari
lokasi pertama dan kedua.
• Ratio estimate
𝑌𝑅 =
(22)(200 + 300)
(4 + 5)
= 1222
• Jumlah all possible sample adalah
𝑁
𝑛
=
4
2
= 6
Sampel (1,2) (1,3) (1,4) (2,3) (2,4) (3,4)
𝑌𝑅 1222 1283 1467 1354 1540 1523

141. • Oleh karena itu setiap sampel mempunyai peluang yang
sama yaitu P(s)=1/6
𝐸 𝑌𝑅 = 𝑌𝑅 𝑃 𝑠 = 1398,17
𝑌 = 1400
𝑀𝑆𝐸 𝑌𝑅 = (𝑌𝑅𝑠 − 𝑌)2
𝑃 𝑠 = 14451,2
6
𝑠=1
𝑀𝑆𝐸 𝑌𝑅 = 14451,2 = 120
𝐵𝑖𝑎𝑠 = 1398,17 − 1400 = −1,83
𝐵𝑖𝑎𝑠2 = 3,4
𝑉 𝑌𝑅 = 14487,8

142. Efisiensi Ratio Estimator Terhadap SRS
• Varians SRS
𝑣 𝑌𝑠𝑟𝑠 = 𝑁2(1 − 𝑓) ∙
𝑠𝑦
2
𝑛
• Varians ratio estimator
𝑣 𝑌𝑅 =
𝑁2
(1 − 𝑓)
𝑛
∙ 𝑠𝑦
2 − 2𝑅𝜌𝑠𝑦𝑠𝑥 + 𝑅2𝑠𝑥
2
• Efisiensi:
𝑣 𝑌𝑅
𝑣 𝑌𝑠𝑟𝑠
=
𝑠𝑦
2 − 2𝑅𝜌𝑠𝑦𝑠𝑥 + 𝑅2𝑠𝑥
2
𝑠𝑦
2

143. • Ratio estimator akan lebih efisien daripada SRS jika:
𝑣 𝑌𝑅
𝑣 𝑌𝑠𝑟𝑠
< 1
𝑠𝑦
2 − 2𝑅𝜌𝑠𝑦𝑠𝑥 + 𝑅2𝑠𝑥
2
𝑠𝑦
2 < 1
𝑠𝑦
2 − 2𝑅𝜌𝑠𝑦𝑠𝑥 + 𝑅2𝑠𝑥
2 < 𝑠𝑦
2
−2𝑅𝜌𝑠𝑦𝑠𝑥 + 𝑅2
𝑠𝑥
2
< 0
2𝑅𝜌𝑠𝑦𝑠𝑥 > 𝑅2𝑠𝑥
2
𝜌 >
𝑅𝑠𝑥
2𝑠𝑦
𝝆 >
𝑪𝑽(𝒙)
𝟐𝑪𝑽(𝒚)

144. Ratio Estimator Pada Stratified Sampling
Ratio Estimator
untuk Stratified
Sampling
Separate Ratio
estimator
Combined Ratio
Estimator

145. Separate Ratio Estimator
Penghitungan rasio dilakukan untuk masing-masing strata
𝑅ℎ =
𝑦ℎ
𝑥ℎ
=
𝑌ℎ
𝑋ℎ
Estimasi total:
𝒀𝑹𝒔 =
𝒚𝒉
𝒙𝒉
𝑳
𝒉=𝟏
∙ 𝑿𝒉 = 𝑹𝒉𝑿𝒉
𝑳
𝒉=𝟏
𝒗 𝒀𝑹𝒔 =
𝑵𝒉
𝟐
𝟏 − 𝒇𝒉
𝒏𝒉
𝒔𝒚𝒉
𝟐
− 𝟐𝑹𝒉𝝆𝒉𝒔𝒚𝒉𝒔𝒙𝒉 + 𝑹𝒉
𝟐
𝒔𝒙𝒉
𝟐
𝑳
𝒉=𝟏
Formula di atas akan valid jika jumlah sampel di setiap strata cukup besar sehingga
aproksimasi rumus varians bisa diterapkan untuk masing-masing strata.
Di samping itu, jika jumlah sampel tiap strata kecil dan jumlah strata besar, biasnya
akan besar.

146. Latihan 3
• Suatu survei stratified random sampling dilakukan di suatu desa untuk mengetahui
pendapatan per kapita di desa tersebut. RW dianggap sebagai strata dan setiap RW diambil
sampel sebanyak 8 rumah tangga. Data yang diperoleh:
a. Perkirakan pengeluaran rata-rata perkapita di desa tsb beserta standar error, RSE, dan
95%CI-nya dengan metode separate ratio estimator.
b. Perkirakan pengeluaran rata-rata per rumah tangga di desa tsb beserta standar error, RSE,
dan 95%CI-nya dengan metode separate ratio estimator.
c. Perkirakan pengeluaran total di desa tsb beserta standar error, RSE, dan 95%CI-nya
dengan metode separate ratio estimator.
Strata
Populasi Sampel
Ruta Penduduk Variabel
Ruta
1
Ruta
2
Ruta
3
Ruta
4
Ruta
5
Ruta
6
Ruta
7
Ruta
8
RW 1 62 217
Pengeluaran 1000 1250 1400 1325 1174 1100 1450 1549
ART 3 4 4 3 2 4 5 3
RW 2 90 288
Pengeluaran 2250 1846 2094 2400 2350 1975 2000 2125
ART 4 2 3 3 3 2 3 4
RW 3 88 352
Pengeluaran 1500 1650 1742 1725 1792 1575 1850 1450
ART 4 5 5 6 5 3 6 2

147. Combined Ratio Estimator
Penghitungan rasio berdasarkan estimasi rata-rata atau total
populasi, dan rasio tersebut digunakan untuk semua strata.
𝑅ℎ = 𝑅 =
𝑦𝑠𝑡
𝑥𝑠𝑡
=
𝑊ℎ𝑦ℎ
𝐿
ℎ=1
𝑊ℎ𝑥ℎ
𝐿
ℎ=1
atau
𝑅ℎ = 𝑅 =
𝑌𝑠𝑡
𝑋𝑠𝑡
=
𝑌ℎ
𝐿
ℎ=1
𝑋ℎ
𝐿
ℎ=1
.

148. Combined Ratio Estimator
Estimasi total:
𝑌𝑠𝑡 = 𝑁ℎ𝑦ℎ
𝐿
ℎ=1
→ 𝑦𝑠𝑡 =
𝑌𝑠𝑡
𝑁
𝑋𝑠𝑡 = 𝑁ℎ𝑥ℎ
𝐿
ℎ=1
→ 𝑥𝑠𝑡 =
𝑋𝑠𝑡
𝑁
𝒀𝑹𝒄 = 𝑹𝑿 =
𝒀𝒔𝒕
𝑿𝒔𝒕
∙ 𝑿 =
𝒚𝒔𝒕
𝒙𝒔𝒕
∙ 𝑿
𝒗 𝒀𝑹𝒄 =
𝑵𝒉
𝟐
𝟏 − 𝒇𝒉
𝒏𝒉
𝒔𝒚𝒉
𝟐
− 𝟐𝑹𝝆𝒉𝒔𝒚𝒉𝒔𝒙𝒉 + 𝑹𝟐
𝒔𝒙𝒉
𝟐
𝑳
𝒉=𝟏
Estimator 𝑌𝑅𝑐 tidak memerlukan informasi mengenai 𝑋ℎ , hanya membutuhkan
informasi 𝑋.
Bias dari combined ratio estimator pada umumnya lebih kecil daripada separate ratio
estimator.
Jika jumlah sampel di setiap strata kecil, combined estimator lebih direkomendasikan
untuk digunakan.

149. Latihan 4
Suatu survei stratified random sampling dilakukan di suatu desa untuk mengetahui
pengeluaran untuk bidang pendidikan di desa tersebut. RW dianggap sebagai strata dan
setiap RW diambil sampel sebanyak 8 rumah tangga. Jika diketahui proporsi penduduk
usia sekolah di desa tersebut sebesar 44%, maka perkirakan pengeluaran rata-rata per
rumah tangga di desa tsb beserta standar error, RSE, dan 95%CI-nya dengan metode
combined ratio estimator.
Strata
Populasi Sampel
Ruta Penduduk Variabel
Ruta
1
Ruta
2
Ruta
3
Ruta
4
Ruta
5
Ruta
6
Ruta
7
Ruta
8
RW 1 62 210
Pengeluaran (000 )
1000 1250 1400 1325 1174 1100 1450 1549
ART usia sekolah 2 2 3 2 1 3 4 2
RW 2 90 288
Pengeluaran
(000)
2250 1846 2094 2400 2350 1975 2000 2125
ART usia sekolah 3 1 2 2 3 1 2 4
RW 3 88 352
Pengeluaran
(000 )
1500 1650 1742 1725 1792 1575 1850 1450
ART usia sekolah 3 4 4 3 4 2 5 1

150. PerbandinganEfisiensi CombineddanSeparateRatioEstimator
• Selisih varians:
𝑣 𝑌𝑅𝑐 − 𝑣 𝑌𝑅𝑠
=
𝑁ℎ
2
1 − 𝑓ℎ
𝑛ℎ
𝑅2
− 𝑅ℎ
2
𝑠𝑥ℎ
2
− 2 𝑅 − 𝑅ℎ 𝜌ℎ𝑠𝑦ℎ𝑠𝑥ℎ
𝐿
ℎ=1
=
𝑁ℎ
2
1 − 𝑓ℎ
𝑛ℎ
𝑅2
− 𝑅ℎ
2
𝑠𝑥ℎ
2
+ 2 𝑅ℎ − 𝑅 𝜌ℎ𝑠𝑦ℎ𝑠𝑥ℎ
𝐿
ℎ=1
Jika jumlah sampel di setiap strata besar dan 𝑅ℎ perbedaannya signifikan
antarstrata, pada umumnya separate estimator lebih efisien daripada
combined estimator.

151. Bivariate Ratio Estimator
• Bivariate ratio estimator adalah estimasi rasio yang
memanfaatkan dua variabel pendukung untuk
memaksimalkan ketelitian (presisi) dari estimasi nilai
karakteristik yang diteliti.
• Jika 𝑦 menunjukkan variabel yang diteliti, dan 𝑥1 dan 𝑥2
merupakan variabel pendukung, penduga 𝑦𝐵𝑅 adalah
𝑦𝐵𝑅 = 𝑤1𝑦𝑅1 + 𝑤2𝑦𝑅2
𝑣 𝑦𝐵𝑅 = 𝑤1
2
𝑣(𝑦𝑅1) + 𝑤2
2
𝑣 𝑦𝑅2 + 2𝑤1𝑤2 𝑐𝑜𝑣(𝑦𝑅1, 𝑦𝑅2)

152. Bivariate Ratio Estimator
• Keterangan:
𝑣 𝑦𝑅1 = 𝑣 𝑦 − 2𝑅1 𝑐𝑜𝑣 𝑦, 𝑥1 + 𝑅1
2
𝑣(𝑥1)
𝑣 𝑦𝑅2 = 𝑣 𝑦 − 2𝑅2 𝑐𝑜𝑣 𝑦, 𝑥2 + 𝑅2
2
𝑣(𝑥2)
𝑐𝑜𝑣 𝑦𝑅1, 𝑦𝑅2 = 𝑣 𝑦 + 𝑅1𝑅2 𝑐𝑜𝑣 𝑥1, 𝑥2 − 𝑅1 𝑐𝑜𝑣 𝑦, 𝑥1 − 𝑅2 𝑐𝑜𝑣 𝑦, 𝑥2
Dengan substitusi 𝑤2 = 1 − 𝑤1 dan melakukan formulasi bahwa diferensiasi
varians 𝑣(𝑦𝐵𝑅) terhadap 𝑤1 sama dengan nol , didapatkan penimbang yang
meminimumkan varians:
Nilai 𝑤1 dan 𝑤2 yang meminimumkan varians adalah:
𝑤1 =
𝑣 𝑦𝑅2 − 𝑐𝑜𝑣 𝑦𝑅1, 𝑦𝑅2
𝑣 𝑦𝑅1 + 𝑣 𝑦𝑅2 − 2𝑐𝑜𝑣(𝑦𝑅1, 𝑦𝑅2)
𝑤2 = 1 − 𝑤1

153. Soal-SoalLatihan
1. Buktikan bahwa varians dari penduga rata-rata berdasarkan ratio estimator dari
penarikan sampel secara SRS WOR:
𝑣 𝑦𝑅 =
1 − 𝑓
𝑛
𝑠𝑦
2
− 2𝑅𝑠𝑦𝑥 + 𝑅2
𝑠𝑥
2
dapat dinyatakan dalam bentuk:
𝑣 𝑦𝑅 =
1 − 𝑓
𝑛
𝑦2
𝐶𝑦
2
− 2𝜌𝐶𝑦𝐶𝑥 + 𝐶𝑥
2
Keterangan:
Cy adalah koefisien variasi dari variabel y
Cx adalah koefisien variasi dari variabel x
2. Berikut ini adalah data populasi hipotetis:
a. Hitung nilai rasio populasi 𝑅
b. Lakukan penarikan sampel secara srs wor dengan n=3
c. hitunglah estimasi rasio 𝑅𝑖 untuk all possible sample
d. Hitung bias 𝐸(𝑅 − 𝑅)
e. Hitung varians 𝑉 𝑅
f. Hitung 𝑀𝑆𝐸 𝑅
No 𝒙𝒊 𝒚𝒊
1 3 1
2 1 2
3 2 3
4 5 4
5 4 5

154. Soal-SoalLatihan
3. Varians dari ratio estimator bisa dinyatakan dengan:
𝑆𝑅𝑆 𝑊𝑅 → 𝑣 𝑅 =
1
𝑥2
∙
𝑠𝑑
2
𝑛0
𝑆𝑅𝑆 𝑊𝑂𝑅 → 𝑣 𝑅 =
1
𝑥2
∙
1 − 𝑓
𝑛
∙ 𝑠𝑑
2
Keterangan:
𝑠𝑑
2
=
1
𝑛 − 1
𝑦𝑖 − 𝑅𝑥𝑖
2
𝑛
𝑖=1
Dengan mensubstitusikan rumus di atas ke dalam rumus presisi
𝑑 = 𝑧𝛼/2 ∙ 𝑠𝑒 𝑅 , buktikan bahwa ukuran sampel minimum yang diperlukan
dapat dinyatakan dengan:
𝑆𝑅𝑆 𝑊𝑅 → 𝑛0 =
𝑧𝛼/2
2
𝑠𝑑
2
𝑑2𝑥2
𝑆𝑅𝑆 𝑊𝑂𝑅 → 𝑛 =
𝑛0
1 + 𝑛0/𝑁

155. Soal-SoalLatihan
4. Berikut ini adalah data yang diperoleh dari pilot survei:
Jika untuk survei yang akan datang dikehendaki presisi relatif sebesar 2,5% dari nilai
rasionya 𝑅 , berapakah jumlah sampel yang dibutuhkan:
a. Jika penarikan sampel secara SRS WR 𝛼 = 5%
b. Jika penarikan sampel secara SRS WOR 𝛼 = 5%, 𝑁 = 500
5. Untuk meneliti kondisi pendidikan para penyandang cacat, dilakukan suatu survei
disabilitas di pulau Jawa. Dari 118 kabupaten/kota diambil sampel sebanyak 30
kabupaten/kota secara SRS WOR, kemudian dilakukan pencacahan ke semua SLB
yang ada di kabupaten/kota terpilih. Untuk setiap SLB yang dikunjungi, dilakukan tes
terhadap para penyandang cacat yang belajar di sekolah tersebut. Misalkan, 𝑥𝑖
merupakan jumlah guru yang mengajar di SLB untuk kabupaten/kota ke-i, 𝑦𝑖
merupakan jumlah penyandang cacat yang nilai tesnya berada di atas standar nilai
minimal yang ditetapkan. Ringkasan data yang diperoleh sebagai berikut:
𝑥𝑖 = 225
𝑛
𝑖=1
, 𝑦𝑖 = 1127
𝑛
𝑖=1
, 𝑥𝑖𝑦𝑖 = 14977
𝑛
𝑖=1
, 𝑥𝑖
2
= 3005
𝑛
𝑖=1
, 𝑦𝑖
2
= 75281
𝑛
𝑖=1
Dengan ratio estimator, perkirakan total penyandang cacat di pulau Jawa yang
nilainya berada di atas standar minimal beserta standar error, RSE, dan 95%
Confidence Interval.
No 1 2 3 4 5 6 7 8 9 10
𝑥𝑖 20 10 30 40 20 15 25 30 20 20
𝑦𝑖 4 2 6 8 5 2 5 6 4 4

156. Soal-SoalLatihan
6. Berikut ini adalah data yang diperoleh dari penarikan sampel industri
mikro di suatu kecamatan.
Jika sampel di atas diambil secara SRS WOR dari populasi N=80 industri
dan diketahui jumlah tenaga kerja industri mikro di kecamatan tersebut
sebanyak 264 orang, serta jumlah input industri mikro sebanyak 1200,
maka:
a. Perkirakan rata-rata output dengan metode ratio estimator berdasarkan
variabel pendukung jumlah tenaga kerja, beserta standar error, dan RSE-
nya.
b. Perkirakan rata-rata output dengan metode ratio estimator berdasarkan
variabel pendukung jumlah input, beserta standar error, dan RSE-nya.
c. Perkirakan rata-rata output dengan metode bivariate ratio estimator
berdasarkan variabel pendukung jumlah tenaga kerja dan jumlah input,
beserta standar error, dan RSE-nya.
d. Bandingkan efisiensi dari ketiga metode di atas.
No 1 2 3 4 5 6 7 8
Pekerja 2 3 5 4 2 3 4 1
Input 12 14 15 15 10 12 10 12
Output 14 14 24 16 10 15 11 16

157. Soal-SoalLatihan
7. Sampel sebanyak 50 kota diambil dari populasi sebanyak 200 kota.
𝑦 menyatakan jumlah penduduk tahun 2012, 𝑥1 menyatakan jumlah
penduduk tahun 2002, 𝑥2 menyatakan jumlah penduduk tahun 1992
Dari data populasi diperoleh:
𝑌 = 1699
𝑋1 = 1482
𝑋2 = 1420
Dari data sampel diperoleh:
𝑦 = 1896 ; 𝑥1 = 1693 ; 𝑥2 = 1643
𝐶𝑦
2
= 1,213 ; 𝐶𝑥1
2
= 1,302 ; 𝐶𝑥2
2
= 1,381
𝜌𝑦,𝑥1𝐶𝑦𝐶𝑥1 = 1,241
𝜌𝑦,𝑥2𝐶𝑦𝐶𝑥2 = 1,256
𝜌𝑥1,𝑥2𝐶𝑥1𝐶𝑥2 = 1,335

158. Soal-SoalLatihan
Keterangan: 𝐶𝑦, 𝐶𝑥1, 𝐶𝑥2 masing-masing merupakan koefisien variasi dari
𝑦 , 𝑥1, dan 𝑥2
Pertanyaan:
a. Perkirakan rata-rata jumlah penduduk per kota tahun 2012 dengan
menggunakan rata-rata sampel acak sederhana, lengkapi dengan
standar error dan RSE-nya.
b. Perkirakan rata-rata jumlah penduduk per kota tahun 2012 dengan
menggunakan ratio estimator berdasarkan variabel pendukung jumlah
penduduk tahun 2002, lengkapi dengan standar error dan RSE-nya.
c. Perkirakan rata-rata jumlah penduduk per kota tahun 2012 dengan
menggunakan ratio estimator berdasarkan variabel pendukung jumlah
penduduk tahun 1992, lengkapi dengan standar error dan RSE-nya.
d. Perkirakan rata-rata jumlah penduduk per kota tahun 2012 dengan
menggunakan bivariate ratio estimator, lengkapi dengan standar error
dan RSE-nya.

159. Soal-SoalLatihan
8. Suatu pilot survei dengan sampel sebanyak 21 rumah tangga digunakan
untuk meneliti jumlah anggota rumah tangga 𝑥 , anak usia sekolah
𝑦1 , mobil yang dimiliki 𝑦2 , dan TV yang dimiliki 𝑦3 . Statistik
deskriptif yang diperoleh:
𝑥 = 3,9 𝑠𝑥 = 1,3
𝑦1 = 1,8 𝑠𝑦1 = 1,2 𝜌𝑦1,𝑥 = 0,97
𝑦2 = 1,2 𝑠𝑦2 = 0,6 𝜌𝑦2,𝑥 = 0,26
𝑦3 = 0,9 𝑠𝑦3 = 0,6 𝜌𝑦3,𝑥 = 0,10
Jika diasumsikan jumlah anggota rumah tangga dari seluruh populasi
𝑋 diketahui, bagaimana pendapat anda jika untuk memperkirakan
total anak usia sekolah, total mobil yang dimiliki, dan total TV yang
dimiliki, ratio estimator lebih dipilih daripada menggunakan estimasi
berdasarkan sampel acak sederhana ?

160. Soal-SoalLatihan
9. Survei Industri Tekstil dan Pengolahan Tekstil (TPT) dilakukan di salah satu provinsi di
Indonesia. Populasi industri TPT di provinsi tersebut dikelompokkan menjadi 2 strata:
Strata 1: Industri TPT yang berorientasi pasar ekspor
Strata 2: Industri TPT yang berorientasi pasar domestik.
Untuk strata 1 dilakukan pendataan secara sensus. Untuk strata 2 dilakukan survei
dengan pengambilan sampel secara SRS WOR.
a. Dengan menggunakan metode combined ratio estimator, perkirakan rasio output tahun
2012 terhadap output tahun 2011 beserta standar error dan RSE-nya.
b. Berdasarkan selang kepercayaan 95%, apakah sudah cukup bukti untuk menyimpulkan
terjadi penurunan nilai output industri tekstil di provinsi tersebut dari tahun 2011 ke
tahun 2012 ? Berikan penjelasan.
c. Perkirakan total nilai output tahun 2011 beserta standar error, RSE, dan 95%
Confidence Interval-nya
Strata
Populasi Sampel
Jumlah
Industri
Nilai
Output
2011
Tahun
Nilai Output (juta Rp)
1 2 3 4 5 6 7 8
1 4 352
2011 96 64 120 72 - - - -
2012 84 72 114 60 - - - -
2 20 348
2011 16 24 8 12 4 32 28 12
2012 15 20 10 9 4 36 30 8

161. TERIMA KASIH
Have A Nice Sampling