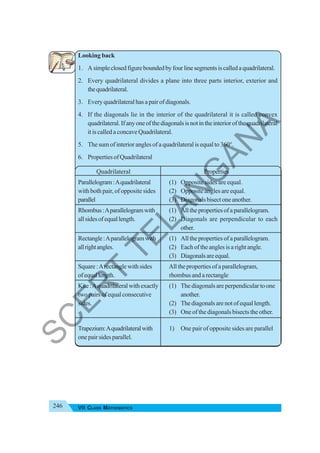
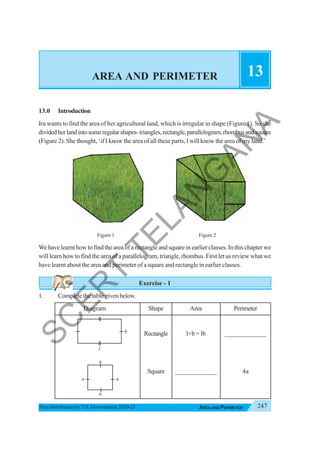
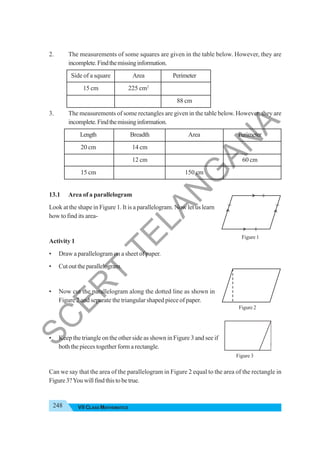
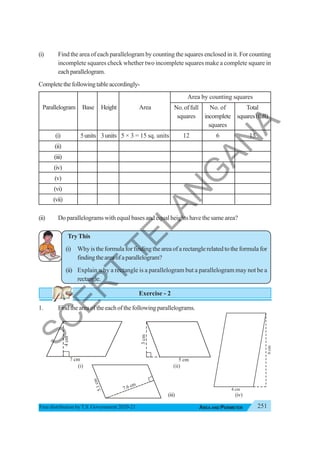
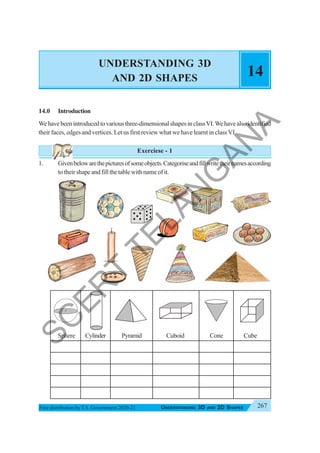
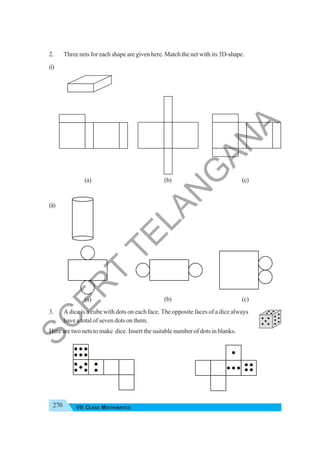
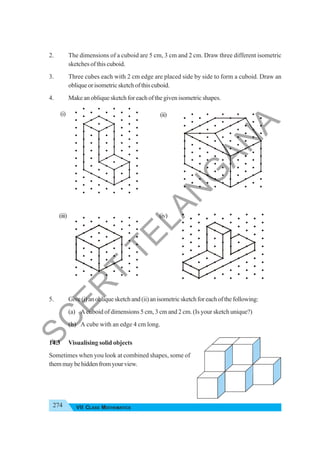
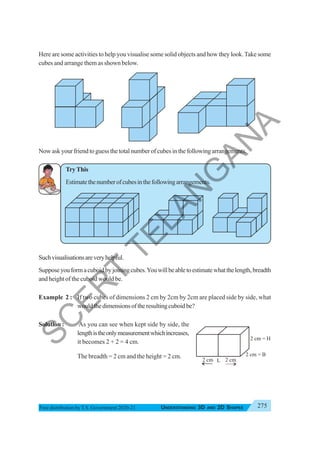
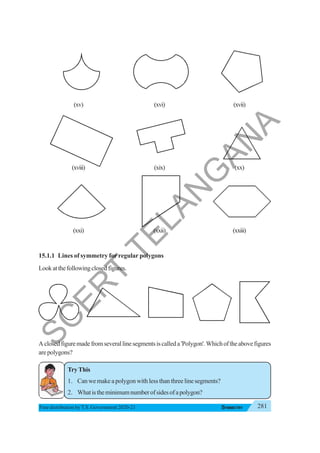
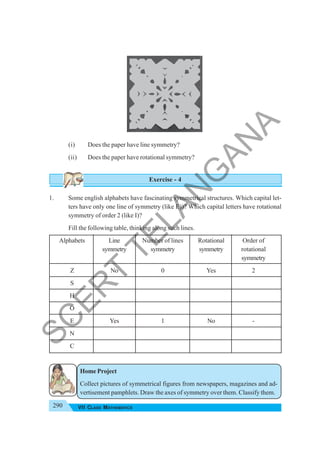
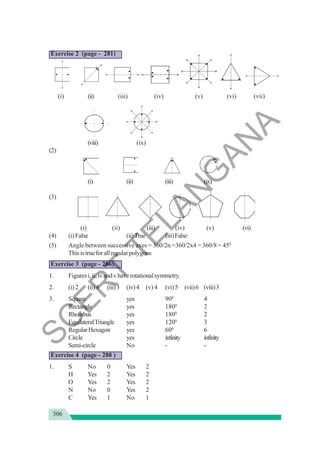
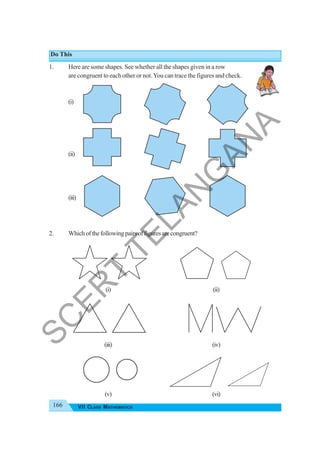
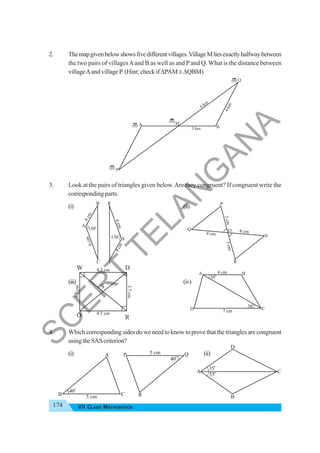
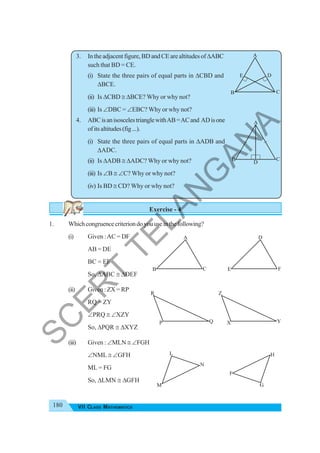
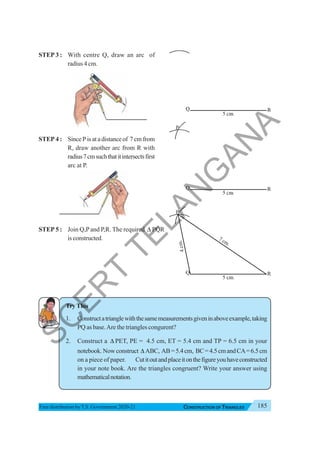
The document provides instructional guidance for mathematics education, emphasizing the importance of real-life contexts and collaborative learning among students and teachers. It outlines various activities, exercises, and projects aimed at enhancing conceptual understanding of mathematical principles, while encouraging students to engage actively in problem-solving and critical thinking. The document also includes a detailed syllabus for the 7th-grade mathematics curriculum, covering essential topics such as integers, fractions, and geometry.















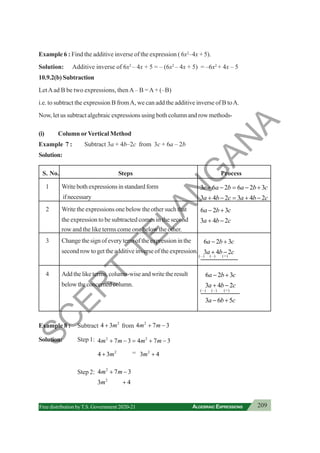
![9
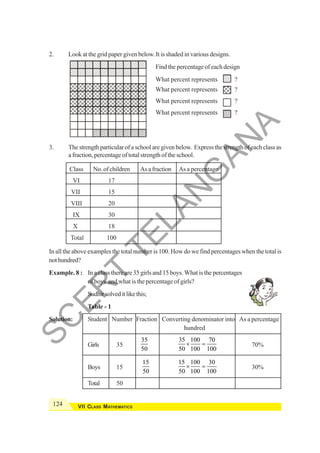
INTEGERS
Free distribution byT.S. Government 2020-21
You have also observed that.
–3 × –1 = 3 –4 × –1 = 4
–3 × –2 = 6 –4 × –2 = 8
–3 × –3 = 9 –4 × –3 = 12
Thus,everytimeifwemultiplytwonegativeintegers,theproductisalwaysapositiveinteger.
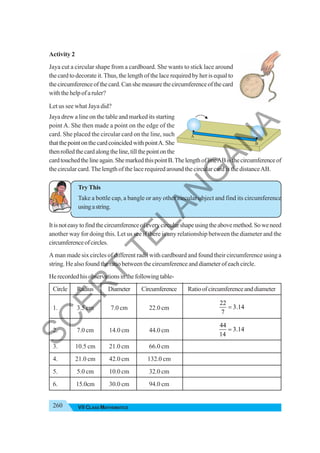
Activity 1
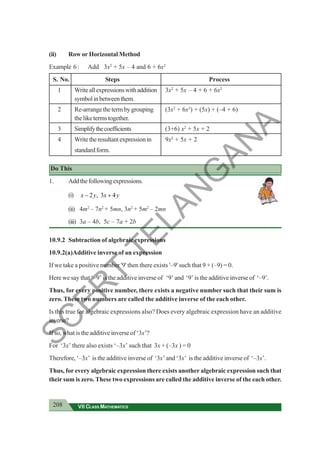
Fillthegridbymultiplyingeachnumberinthefirstcolumnwitheachnumberinthefirstrow.
× 3 2 1 0 –1 –2 –3
3 9 6 3 0 –3 –6 –9
2 6 4 2 0
1
0
–1 –3 –2 –1 0 1 2 3
–2
–3
(i) Is the product of two positive integers always a positive integer?
(ii) Is the product of two negative integers always a positive integer?
(iii) Is the product of a negative and positive integer always a negative integer?
1.1.3(b) Multiplication of more than two negative integers
We observed that the product of two negative integers is a positive integer. What will be the
product of three negative integers? Four negative integers? and so on .....
Letusstudythefollowingexamples.
(i) (–2) × (–3) = 6
(ii) (–2) × (–3) × (–4) = [(–2) × (–3)] × (–4) = 6 × (–4) = – 24
(iii) (–2) × (–3) × (–4) × (–5) = [(–2) × (–3) × (–4)] × (–5) = (–24) × (–5) = 120
(iv) [(–2) × (–3) × (–4) × (–5) × (–6)] = 120 × (–6) = –720
S
C
E
R
T
T
E
L
A
N
G
A
N
A](https://image.slidesharecdn.com/7mathsem2020-21-240629141640-7e5c629a/85/Mathematics-7th-class-English-medium-text-book-17-320.jpg)



![VII CLASS MATHEMATICS
14
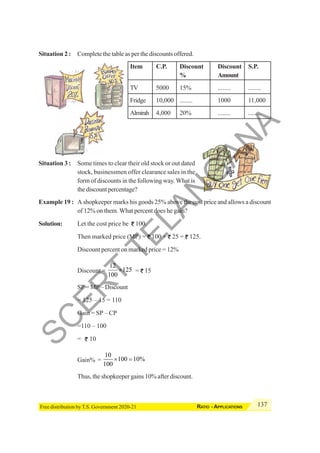
(ii) Commutativeproperty
Studythefollowingandfillintheblanks.
Statement 1 Statement 2 Conclusion
4 + 3 = 7 3 + 4 = 7 4 + 3 = 3 + 4 = 7
3 + 5 = 5 + 3 =
3 + 1 = 1 + 3 =
Similarly, add as many pairs of whole numbers, as you wish. Did you find any pair of whole
numbers for which the sum is different, when the order is changed.You will not find such a pair.
Thus,wesaythattheadditionofwholenumbersiscommutative.
Isadditionofintegerscommutative?Studythefollowingandfillintheblanks.
Statement 1 Statement 2 Conclusion
5 + (–6) = –1 (–6) + 5 = –1 5 + (–6) = (–6) + 5 = –1
–9 + 2 = 2 + (–9) =
–4 + (–5) = (–5) + (–4) =
Did you find any pair of integers for which the sum is different when the order is changed?You
would have not. Therefore, addition is commutative for integers.
In general, for any two integers a and b, a + b = b + a
(iii) Associative property
Letusstudythefollowingexamples-
(i) (2 + 3) + 4 2 + (3 + 4)
= 5 + 4 = 2 + 7
= 9 = 9
(ii) (–2 + 3) + 5 –2 + (3 + 5)
= 1 + 5 = –2 + 8
= 6 = 6
(iii) (–2 + 3) + (–5) (- 2) + [3 + (–5)]
= 1 + (–5) = (- 2) + (-2)
= –4 = –4
(iv) [(–2) + (–3)] + (-5) –2 + [(–3) + (–5)]
= –5 + (–5) = –2 + (–8)
= –10 = –10
S
C
E
R
T
T
E
L
A
N
G
A
N
A](https://image.slidesharecdn.com/7mathsem2020-21-240629141640-7e5c629a/85/Mathematics-7th-class-English-medium-text-book-22-320.jpg)

![17
INTEGERS
Free distribution byT.S. Government 2020-21
TryThis
1. Multiplythefollowing
(i) 2 × 3 = _______
(ii) 5 × 4 = _______
(iii) 3 × 6 = _______
2. Similarly,multiplyanytwowholenumbersofyourchoice.
Is the product of two whole numbers always a whole number?
(ii) Commutativeproperty
We know that multiplication is commutative for whole numbers. Is it also commutative
for integers?
Statement 1 Statement 2 Conclusion
5 × (–2) = –10; (–2) × 5 = –10 5 × (–2) = (–2) × 5 = –10
(–3) × 6 = 6 × (–3) =
–20 × 10 = 10 × (–20) =
Therefore, multiplication of integers follows the commutative property.
In general, for any two integers a and b, a × b = b × a
(iii) Associative property
Consider the multiplication of 2, –3, –4 grouped as follows.
[2 × (–3)] × (–4) and 2 × [(–3) × (–4)]
We see that-
[2 × (–3)] × (–4) and 2 × [(–3) × (–4)]
= (–6) × (–4) = 2 × 12
= 24 = 24
In first case 2, –3 are grouped together and in the second –3, –4 are grouped together. In both
cases the product is the same.
Thus, [2 × (–3)] × [(–4)] = 2 × [(–3) × (–4)]
Does the grouping of integers affect the product of integers? No, it does not.
The product of three integers does not depend upon the grouping of integers. Therefore, the
multiplication of integers is associative.
In general, for any integers, a, b and c, (a × b) × c = a × (b × c)
S
C
E
R
T
T
E
L
A
N
G
A
N
A](https://image.slidesharecdn.com/7mathsem2020-21-240629141640-7e5c629a/85/Mathematics-7th-class-English-medium-text-book-25-320.jpg)
![VII CLASS MATHEMATICS
18
Do This
1. Is [(–5) × 2)] × 3 = (–5) × [(2 × 3)]?
2. Is [(–2) × 6] × 4 = (–2) × [(6 × 4)]?
Try This
(5 × 2) × 3= 5 × (2 × 3)
Is the associative property true for whole numbers?Take many more examples and
verify.
(iv) Distributive property
We know that, 9 × (10 + 2) = (9 × 10) + (9 × 2)
Thus,multiplicationdistributesoveradditionistrueforwholenumbers.
Let us see, is this true for integers-
(i) –2 × (1 + 3) = [(–2) x 1] + [(–2) × 3]
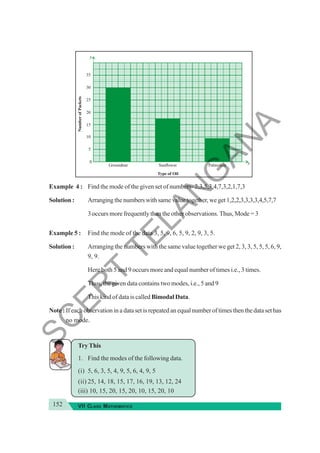
–2 × 4 = –2 + (–6)
–8 = –8
(ii) –1 × [3 + (–5)]= [(–1) × 3] + [(–1) × (–5)]
–1 × (–2) = –3 + (+5)
2 = 2
Verify –3 × (–4+2) = [(–3) × (–4)] + [–3 × (2)]
You will find that in each case, the left hand side is equal to the right hand side.
Thus,multiplicationdistributesoveradditionofintegerstoo.
In general, for any integers a, b and c, a × (b + c) = a × b + a × c
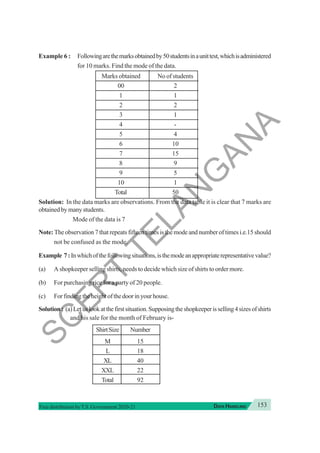
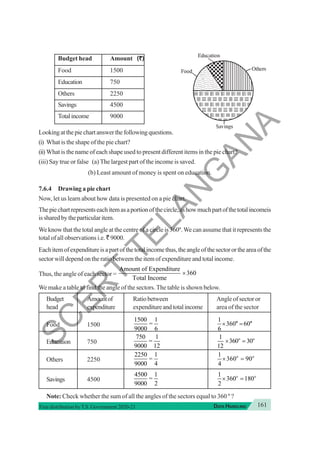
S
C
E
R
T
T
E
L
A
N
G
A
N
A](https://image.slidesharecdn.com/7mathsem2020-21-240629141640-7e5c629a/85/Mathematics-7th-class-English-medium-text-book-26-320.jpg)
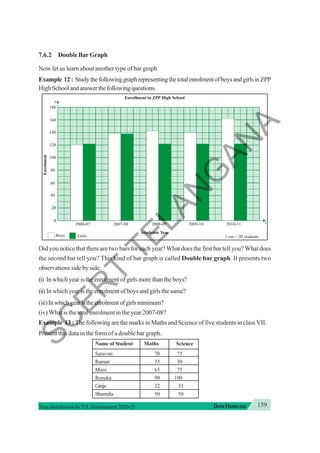
![19
INTEGERS
Free distribution byT.S. Government 2020-21
(v) Multiplicative identity
2 × 1 = 2
–5 × 1 = –5
–3 × 1 = _____
–8 × 1 = _____
1 × –5 = _____
You will find that multiplying an integer by 1 does not change the integer. Thus, 1 is called the
multiplicativeidentityforintegers.
In general, for any integer ‘a’, a × 1 = 1 × a = a
(vi) Multiplication by zero
We know that any whole number when multiplied by zero gives zero.What happens in case of
integers?Study thefollowing-
(–3) × 0 = 0
0 × (–8) = ——
9 × 0 = ——
This shows that the product of an integer and zero is zero.
In general for any integer a, a × 0 = 0 × a = 0
Exercise - 5
1. Verifythefollowing.
(i) 18 × [7 + (–3)] = [18 × 7] + [18 × (–3)]
(ii) (–21) × [(–4) + (–6)] = [(–21) × (–4)] + [(–21) × (–6)]
2. (i) For any integer a, what is (–1) × a equal to?
(ii) Determine the integer whose product with (–1) is 5
3. Findtheproduct,usingsuitableproperties.
(i) 26 × (–48) + (–48) × (–36) (ii) 8 × 53 × (–125)
(iii) 15 × (–25) × (–4) × (–10) (iv) (–41) × 102
(v) 625 × (–35) + (–625) × 65 (vi) 7 × (50 – 2)
(vii) (–17) × (–29) (viii) (–57) × (–19) + 57
1 is the multiplicative identity of
integers
S
C
E
R
T
T
E
L
A
N
G
A
N
A](https://image.slidesharecdn.com/7mathsem2020-21-240629141640-7e5c629a/85/Mathematics-7th-class-English-medium-text-book-27-320.jpg)

![VII CLASS MATHEMATICS
22
Try This
1. For any integer a, is
(i) a ÷ 1 = 1?
(ii) a ÷ (–1) = –a?
Take different values of ‘a’and check.
(iii) Associative property
Is [(–16) ÷ 4] ÷ (–2) = (–16) ÷ [4 ÷ (–2)]?
[(–16) ÷ 4] ÷ (–2) = (–4) ÷ (–2) = 2
(–16) ÷ [4 ÷ (–2)] = (–16) ÷ (–2) = 8
Therefore,[(–16) ÷ 4] ÷ (–2) ≠ (–16) ÷ [4 ÷ (–2)]
Thus,divisionofintegersisnotassociative.
Try This
Takeatleastfivemoreexamplesandcheckwhetherdivisionisassociativeforintegers.
Exercise - 6
1. Fillthefollowingblanks.
(i) –25 ÷ ........ = 25
(ii) ........ ÷ 1 = –49
(iii) 50 ÷ 0 = .....................
(iv) 0 ÷ 1 = .....................
1.3 Some practical problems using negative numbers
Example 1 : In a test (+5) marks are given for every correct answer and (–2) marks are given
for every incorrect answer. (i) Radhika answered all the questions and scored 30
marks through 10 correct answers. (ii) Jaya also answered all the questions and
scored(–12)marksthrough4correctanswers.Howmanyincorrectanswershad
both Radhika and Jaya attempted?
Solution: (i) Marks given for one correct answer = 5
So marks given for 10 correct answers = 5 × 10 = 50
Radhika’s score = 30
Marks obtained for incorrect answers = 30 – 50 = –20
Marks given for one incorrect answer = (–2)
Therefore,numberofincorrectanswers = (–20) ÷ (–2) = 10
S
C
E
R
T
T
E
L
A
N
G
A
N
A](https://image.slidesharecdn.com/7mathsem2020-21-240629141640-7e5c629a/85/Mathematics-7th-class-English-medium-text-book-30-320.jpg)














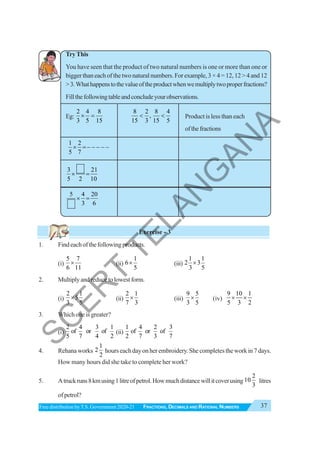






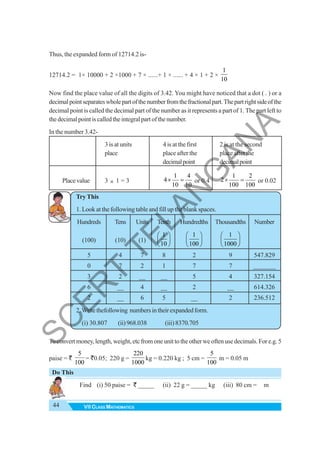












































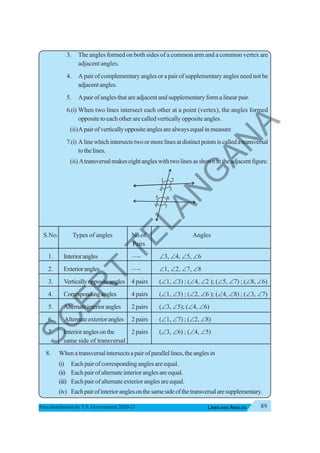
![90 VII CLASS MATHEMATICS
TRIANGLE AND ITS PROPERTIES 5
5.0 Introduction
You have been introduced to triangles in your previous class. Look at the figures given below.
Whichofthesearetriangles?
(i) (ii) (iii) (iv)
Discusswithyourfriendswhyyouconsideronlysomeoftheseastriangles.
Atriangleisaclosedfiguremadeupofthreelinesegments.
In ΔPQR, the:
(i) Three sides are PQ,QR,RP
(ii) Three angles are ∠RQP, ∠QPR, ∠PRQ
(iii) Three vertices are P, Q, R
ThesideoppositetovertexPis QR CanyounamethesideswhichareoppositetoverticesQandR?
Likewise, the side opposite to∠QPRis QR . Can you name the side which is opposite to∠RQP
Try This
Umafeltthatatrianglecanbeformedwiththreecollinearpoints.Doyouagree?Why?
Drawdiagramstojustifyyouranswer.
[If three or more points lie on the same line, then they are called collinear points]
Note: LM = Length of Line segment of LM ; LM = Line segment LM
LM
JJJG
= Ray LM ; LM
HJJG
= Line LM
P
Q R
S
C
E
R
T
T
E
L
A
N
G
A
N
A](https://image.slidesharecdn.com/7mathsem2020-21-240629141640-7e5c629a/85/Mathematics-7th-class-English-medium-text-book-98-320.jpg)


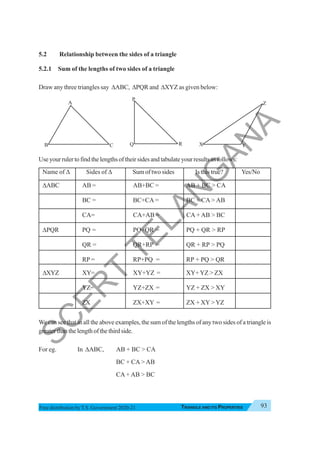
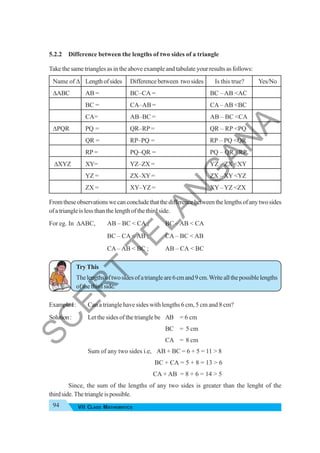




![Triangle and Its Properties 99
TRIANGLE AND ITS PROPERTIES
Free distribution byT.S. Government 2020-21
Proof:
Marktheanglesasindicatedinthefigure:
∠2 = ∠5 (alternateinteriorangles)
∠3 = ∠4 (alternateinteriorangles)
∠2 + ∠3 = ∠5 + ∠4 (adding (1) and (2))
∠1 + ∠2 + ∠3 = ∠1 + ∠5 + ∠4 (adding ∠1 to both sides)
But ∠1 + ∠5 + ∠4 = 180o
(anglesformingastraightline)
Therefore, ∠1 + ∠2 + ∠3 = 180o
∴
∠A + ∠B + ∠C = 180o
.
Thus, the sum of the angles of a triangle is 180o
.
Example 1: In ΔABC, ∠A = 30o
, ∠B = 45o
, find ∠C.
Solution : In ΔABC, ∠A + ∠B + ∠C = 180o
(angle-sumpropertyofatriangle)
30o
+ 45o
+ ∠C = 180o
(substitutinggivenvaluesinquestion)
75o
+ ∠C = 180o
∠C = 180o
– 75o
Therefore, ∠C = 105o
Example 2 : In ΔABC, if ∠A = 3 ∠B and ∠C = 2 ∠B. Find all the three angles of ΔABC.
Solution : ∠A + ∠B + ∠C = 180o
[angle-sumpropertyofatriangle]
3 ∠B + ∠B + 2 ∠B = 180o
[∠A = 3 ∠B, ∠C = 2 ∠B]
6 ∠B = 180o
Therefore, ∠B = 30o
Thus, ∠A = 3 ∠B = 3 × 30o
= 90o
∠C = 2 ∠B = 2 × 30o
= 60o
Example 3 : ΔABC is right angled at C and CD⊥AB, ∠A = 55o
Find (i)∠DCA (ii) ∠BCD (iii) ∠ABC
Solution : In ΔACD,
∠CAD + ∠ADC + ∠DCA = 180o
(angle-sum property of a triangle)
55o
+ 90o
+ ∠DCA = 180o
(substituingvaluesgiveninquestion)
A
B
C
55o
D
S
C
E
R
T
T
E
L
A
N
G
A
N
A](https://image.slidesharecdn.com/7mathsem2020-21-240629141640-7e5c629a/85/Mathematics-7th-class-English-medium-text-book-107-320.jpg)




















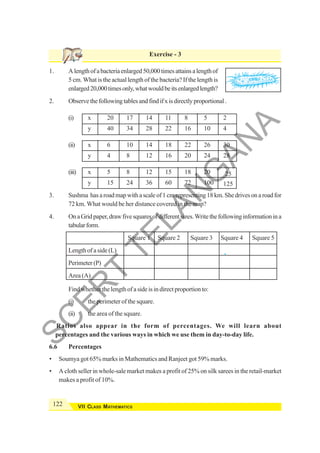



















































































![232 VII CLASS MATHEMATICS
Is the sum of the angles ∠1, ∠2, ∠3 and ∠4 equal to 360o
? (sumofanglesatapoint)
The sum of the four angles of a quadrilateral is 360°.
[Note: We can denote the angles by ∠1, ∠2, ∠3, etc., as their respective measures i.e. m∠1,
m∠2, m∠3, etc.]
You may arrive at this result in several other ways also.
1. Let Pbe any point in the interior of quadrilateralABCD. Join Pto verticesA, B, C and D.
In the figure, consider ΔPAD.
m∠2 + m∠3= 180° – x ................ (1)
Similarly, in ΔPDC, m∠4 + m∠5 = 180° – y ....... (2)
in ΔPCB, m∠6 + m∠7 = 180º – z and ............ (3)
in ΔPBA, m∠8 + m∠1 = 180º – w. ................. (4)
(angle-sumpropertyofatriangle)
Adding (1), (2), (3) and (4) we get
m∠1 + m∠2 + m∠3 + m∠4 + m∠5 + m∠6 + m∠7 + m∠8
= 180° – x + 180° – y + 180° – z + 180° – w
= 720° – (x + y + z + w)
(x + y + z + w = 360o
; sum of angles at a point)
=720° – 360° = 360°
Thus, the sum of the angles of the quadrilateral is 360o
.
2. Take any quadrilateral, sayABCD. Divide it into two tri-
angles, by drawing a diagonal.You get six angles 1, 2, 3, 4,
5 and 6.
Using the angle-sum property of a triangle and you can easily find how the sum of the
measures of ∠A, ∠B, ∠C and ∠D amounts to 360°.
Try This
What would happen if the quadrilateral is not convex? Consider
quadrilateralABCD.Splititintotwotrianglesandfindthesumof
theinteriorangles.Whatisthesumofinterioranglesofaconcave
quadrilateral?
A
D
B
C
A
C
B
D
1
2
8
7
5
6
4
3
y
x
w
z
P
A
C
B
D
3
2
4
1 6
5
S
C
E
R
T
T
E
L
A
N
G
A
N
A](https://image.slidesharecdn.com/7mathsem2020-21-240629141640-7e5c629a/85/Mathematics-7th-class-English-medium-text-book-240-320.jpg)