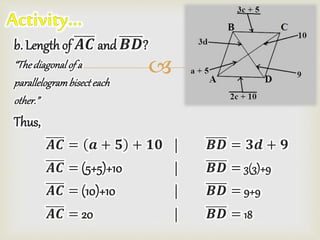
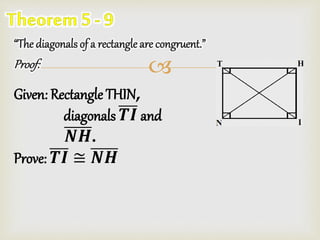
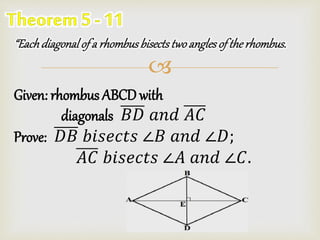
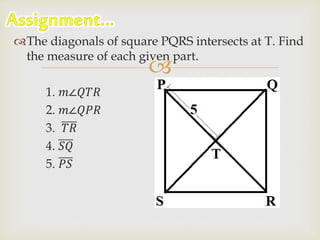
The document contains a prayer asking God for guidance and blessing for the learning that is about to take place. It then lists different shapes - parallelogram, rectangle, rhombus, and square - and provides their key properties. Examples are given to demonstrate properties such as opposite sides being parallel and congruent for parallelograms, diagonals being congruent for rectangles, and diagonals bisecting angles for rhombuses.

2. 
Let us pray!
Dear Lord and Father of all, thank you for today.
Thank you for ways in which you provide for all of
us all. For your protection and love we thank you.
Help us to focus our hearts and minds now on what
we are about to learn.
Inspire us by Your Holy Spirit as we listen and
write. Guide us by your eternal light us we discover
more about the world around us.
We ask all this in the name of Jesus.
Amen.

3. 
Please say presentas I call
your name.

4. 
Parallelogram
 quadrilateral with both pairs of opposite sides that
is parallel.
opposite sides are congruent
opposite angles are congruent

5. 
Using the concept of parallelogram, determine the
unknown.
a. Value of a
andd.
b. Length of
𝑨𝑪 and 𝑩𝑫?
c. Length of
𝑨𝑫 and 𝑩𝑪?

6. 
a. Value of a andd.
“Thediagonalof a parallelogrambisecteachother.”
Thus,
a+5 = 10 and 3d = 9
a = 10-5 d = 3
a = 5

7. 
b. Length of 𝑨𝑪 and 𝑩𝑫?
“Thediagonalof a
parallelogrambisecteach
other.”
Thus,
𝑨𝑪 = 𝒂 + 𝟓 + 𝟏𝟎 | 𝑩𝑫 = 𝟑𝒅 + 𝟗
𝑨𝑪 = (5+5)+10 | 𝑩𝑫 = 3(3)+9
𝑨𝑪 = (10)+10 | 𝑩𝑫 = 9+9
𝑨𝑪 = 20 | 𝑩𝑫 = 18

8. 
c. Length of 𝑨𝑫 and 𝑩𝑪?
“Oppositesidesof a
Parallelogramis congruent.”
Thus, 𝑨𝑫 = 𝑩𝑪
2c + 10 = 3c + 5
10 – 5 = 3c – 2c
5 = c
𝑨𝑫 = 2c + 10 and 𝑩𝑪 = 3c + 5
= 2(5)+10 =3(5)+5
=20 = 20

10. 
Arrange the objects according to its shape.

11. 
Rhombus Rectangle Square

12. 

14. At the end of the lesson, the students must be able to:
a. identify the special properties of a rectangle, rhombus
andsquare;
b. apply the special properties of a rectangle, rhombus
andsquare; and
c. take and pass the test witha mastery level of 75%.

15. 
When all sides of a parallelogram are congruent, it is a
rhombus.
ABCDis a rhombus.

16. 
When all angles of a parallelogramare right, it is a rectangle.
EFGHis a rectangle.

17. 
When the angles of a parallelogramare rights angles andall
its sides are congruent, then it is a square
IJKL is a square.

18. 
“The diagonalsof a rectangle are congruent.”
Proof:
Given: Rectangle THIN,
diagonals 𝑻𝑰 and
𝑵𝑯.
Prove: 𝑻𝑰 ≅ 𝑵𝑯

19. 
 Given: RectangleTHIN, diagonals 𝑻𝑰
and 𝑵𝑯.
 Prove: 𝑻𝑰 ≅ 𝑵𝑯
Proof:
Statements Reasons
Parallelogram THIN is a rectangle. Given
𝑇𝐻 ≅ 𝑁𝐼; 𝑇𝑁 ≅ 𝐻𝐼 Definition of a rectangle.
∠𝑇, ∠𝐻, ∠𝐼 𝑎𝑛𝑑 ∠𝑁 are right angles. Definition of a rectangle.
∠𝑁 ≅ ∠𝐼 All right angles are congruent.
⊿𝑇𝑁𝐼 ≅ ⊿𝐻𝐼𝑁 SAS Congruence Postulate
𝑇𝐼 ≅ 𝑁𝐻 CPCTC

20. 
Thediagonalsof a rhombusareperpendicular.
Given: rhombus LIFE with
diagonals 𝑳𝑭and 𝑬𝑰
Prove: 𝑳𝑭 ⊥ 𝑬𝑰

21. 
 Given: rhombus LIFE with
diagonals 𝑳𝑭and 𝑬𝑰
 Prove: 𝑳𝑭 ⊥ 𝑬𝑰
Proof:
Statements Reasons
𝐿𝐹and 𝐸𝐼 are diagonals Given
𝐿𝑀 ≅ 𝐹𝑀; 𝐸𝑀 ≅ 𝐼𝑀 Diagonals of a rhombus are bisector
of each other.
𝐸𝐿 ≅ 𝐿𝐼 ≅ 𝐸𝐹 ≅ 𝐹𝐼 Definition of a rhombus.
⊿𝐸𝑀𝐿 ≅ ⊿𝐿𝑀𝐼 ≅ ⊿𝐼𝑀𝐹 ≅ ⊿𝐹𝑀𝐸 SSS congruence Postulate
𝑚∠𝐸𝑀𝐿 = 𝑚∠𝐿𝑀𝐼 = 𝑚∠𝐼𝑀𝐹 = 𝑚∠𝐹𝑀𝐸 CPCTC
𝑚∠𝐸𝑀𝐿 + 𝑚∠𝐿𝑀𝐼 + 𝑚∠𝐼𝑀𝐹 + 𝑚∠𝐹𝑀𝐸 = 360° Sum of angles in one revolution.
𝑚∠𝐸𝑀𝐿 = 𝑚∠𝐿𝑀𝐼 = 𝑚∠𝐼𝑀𝐹 = 𝑚∠𝐹𝑀𝐸 = 90° Angle Addition Postulate
𝐿𝐹 ⊥ 𝐸𝐼 Definition of perpendicular lines

22. 
“Eachdiagonalof a rhombusbisectstwoanglesof therhombus.
Given: rhombus ABCD with
diagonals 𝐵𝐷 𝑎𝑛𝑑 𝐴𝐶
Prove: 𝐷𝐵 𝑏𝑖𝑠𝑒𝑐𝑡𝑠 ∠𝐵 𝑎𝑛𝑑 ∠𝐷;
𝐴𝐶 𝑏𝑖𝑠𝑒𝑐𝑡𝑠 ∠𝐴 𝑎𝑛𝑑 ∠𝐶.

23. 
 Given: rhombus ABCDwithdiagonals 𝐵𝐷 𝑎𝑛𝑑 𝐴𝐶
 Prove: 𝐷𝐵 𝑏𝑖𝑠𝑒𝑐𝑡𝑠 ∠𝐵 𝑎𝑛𝑑 ∠𝐷; 𝐴𝐶 𝑏𝑖𝑠𝑒𝑐𝑡𝑠 ∠𝐴 𝑎𝑛𝑑 ∠𝐶.
 Proof:
Statements Reasons
ABCD is a rhombus;
𝐵𝐷and 𝐴𝐶 are diagonals
Given
𝐴𝐵 ≅ 𝐴𝐷 ≅ 𝐶𝐵 ≅ 𝐶𝐷 Definition of a rhombus.
𝐵𝐷 ≅ 𝐵𝐷; 𝐴𝐶 ≅ 𝐴𝐶 Reflexive Property
⊿𝐴𝐵𝐷 ≅ ⊿𝐶𝐵𝐷; ⊿𝐴𝐵𝐶 ≅ ⊿𝐴𝐷𝐶 SSS Congruence Postulate
∠𝐴𝐵𝐷 ≅ ∠𝐶𝐵𝐷and ∠𝐴𝐷𝐵 ≅ ∠𝐶𝐷𝐵;
∠𝐵𝐴𝐶 ≅ ∠𝐷𝐴𝐶and ∠𝐵𝐶𝐴 ≅ ∠𝐷𝐶𝐴
CPCTC
𝐷𝐵 𝑏𝑖𝑠𝑒𝑐𝑡𝑠 ∠𝐵 𝑎𝑛𝑑 ∠𝐷;
𝐴𝐶 𝑏𝑖𝑠𝑒𝑐𝑡𝑠 ∠𝐴 𝑎𝑛𝑑 ∠𝐶
Definition of Angle Bisector.

25. 
I. Determine whether the following is TRUE/FALSE.
1. All squares are rectangles.
2. All rectangles are squares.
3. All parallelogramare rhombuses.
4. Some rectangles are squares.
5. Some rhombuses are squares.

27. 
Given: rhombus EFGH
and 𝒎∠𝑬𝑭𝑮 = 𝟏𝟑𝟎°.
1. What is 𝒎∠𝑬𝑭𝑫? Stateyour reason.
2. What is 𝒎∠𝑫𝑬𝑭? Stateyour reason.

29. 
The diagonals of square PQRS intersects at T. Find
the measure of each given part.
1. 𝑚∠𝑄𝑇𝑅
2. 𝑚∠𝑄𝑃𝑅
3. 𝑇𝑅
4. 𝑆𝑄
5. 𝑃𝑆