This document provides an activity exploring mathematical patterns using blocks. It contains 17 questions for students to explore patterns in addition tables, multiplication tables, squares, cubes, and triangles built with blocks. Some key objectives are to discover algebraic formulas and understand why the product of two negative numbers is positive. The activity is suitable for grades 4-12 and can be done in one or multiple 60-minute sessions using wooden blocks.

1. 0.1 Math Blocks
Everyone loves blocks. Blocks are a wonderful way to see mathematical patterns. This
session explores many patters that may be built from blocks.
Grade Level/Prerequisites: This activity is suitable for students in grades 4 – 12 or
their teachers.
Time: This will fit in a 60 minute session. There is enough material for two or three
sessions.
Materials: A collection of 9/16 inch wooden cubes or 1 inch wooden cubes are required.
A dark color spray paint helps. A chalk board or white board together with a number of
sheets of paper are really useful. Colored chalk or pens also help. Wooden cubes may be
purchased at many craft stores, and on the internet. Optional materials include several
cardboard boxes and string, or the following PVC for a large model:
(1) 3/4-in Dia 45-Degree PVC Sch 40 Elbow (six)
(2) 3/4-in Dia 90-Degree PVC Sch 40 Slip Elbow (two)
(3) 3/4-in x 10-ft 480-PSI Schedule 40 PVC Pipe (two)
(4) Skein of yarn (one)
(5) masking tape
Preparation: Get some wooden blocks and solve the problems on the hand out. Paint
roughly one-half of the blocks. Make enough grid addition tables from 0 + 0 up to 4 + 4
as well as grid multiplication tables from 1 × 1 to 3 × 3 for the number of student teams
you expect. Make any of the models that you will use once before you try with students.
Read the presentation notes. Follow the presentation and only hand the students
the hand-out at the end of the session.
Objectives: Let participants discover and see various algebraic formula and mathematical
patterns. Understand why the product of two negative numbers is a positive number.
References/Authorship: The idea of drawing geometric figures to represent mathemat-
ical patterns has been around for sveral thousand years. Joshua Zucker commented that
it is fun to build the addition table and multiplication table out of legos and that inspired
Dave Auckly to develop this math circle session.
1

2. Math Blocks
In this session you will play with blocks to explore some sequences of numbers, aht addition
table and the multiplication table. You will also get to look at and possibly make some
string art.
Many geometric patterns also include interesting numerical patterns. Here are a few ex-
amples:
Figure 1: Squares and Triangles
Figure 2: Cubes and Tetrahedra
Look for interesting numberical patterns in these figures. You may draw additional shapes
on the grid on the back of this page, and you may make models with the small wooden
cubes. In addition to the shapes described above, make a 3D addition table up to 4 + 4
including both 3 + 4 and 4 + 3, and a 3D multiplication table up to 3 × 3. You may also
wish to color a few more squares in the multiplication table on the grid on the back of this
page.
You may also have fun excivating blocks from the real MineCraft area. You can’t dig the
black bedrock.
Some interesting patterns appear if you look at sections of the addition table over diagonals
connecting 1 + 4 to 4 + 1, look at the analogous sections of the multiplication table over
the same diagonals. These diagonals are collored on part of the grid paper. Look at the
sections of the multiplication table over the L-shaped regions that are also displayed on
the grid paper.
2

3. Figure 3: Multiplication in the grid
(1) How could you comput the square of 7?, of 17? (The number of little squares in S5
is called the square of 5. It is denoted by 52 .)
(2) What can you say about the difference between the number of little squares in square
S2 and S1 ? What about the difference in S3 and S2 ? What about S16 and S15 ?
(3) What can you say about the difference between the number of little squares in triangle
T2 and T1 ? What about the difference in T3 and T2 ? What about T16 and T15 ?
(4) Can you see a way to compute T4 ? Can you see a second way? What about T15 ?
TCAT ?
(5) What is a good way to compute/see the sum 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 +
11 + 12 + 13 + 14?
(6) How many little cubes would we need to build the addition table from 0 + 0 all the
way up to 49 + 49 including both versions of each sum, i.e. 13 + 23 and 23 + 13 for
example would both appear.
(7) How does the value of the sum change when you move up or down a column in the
addition table? What about left or right across a row?
3

4. Figure 4: Multiplication Ls and diagonals
(8) How does the value of the product change when you move up or down a column in
the multiplication table? What about left or right across a row?
(9) What can you say about the sum of the numbers in the third row of the multiplication
table from 3 × 1 to 3 × 7?
(10) What can you say about the sum of the numbers in a multiplication table from 0×0
all the way up to 29 × 29 including both versions of each sum, i.e. 13 × 23 and
23 × 13 for example would both appear.
(11) Can you compute the number of small cubes in cube C12 ? How? (The number of
little cubes in C5 is called the cube of 5. It is denoted by 53 .)
(12) Can you compute/see the diference in the number of small cubes in C15 and C14 ?
How?
(13) Can you see the difference between the number of small cubes in Tet8 and Tet9 ?
(14) What is a good way to compute/see the sum 12 + 22 + 32 + 42 + 52 + 62 + 72 ? Why
might someone think of pyramid numbers?
(15) What can you say about the sum of the numbers in the multiplication table along
the diagonal from 1 × 4 to 4 × 1? What about the analogous diagonals? Can you
see it?
(16) What can you say about the sum of the numbers in the multiplication table along
the L-shapped regions displayed in the grid?
(17) What is a good way to compute/see the sum 13 + 23 + 33 + 43 + 53 + 63 + 73 ?
4

5. Teacher Guide/Solutions
Solutions:
(1) A square of side 7 would have seven rows of seven squares so 7 × 7 = 72 = 49 small
squares. Similarly a square of side 17 would have 17 rows of 17 for 17 × 17 small
squares.
(2) S2 − S1 = 4 − 1 = 3. One also has S3 − S2 = 9 − 4 = 5. In fact the picture shows
this in a nice way. When we take the small square in the upper left (in the case of
Figure 5: Difference of squares version 1
the Figure S2 away from the larger square, in this case S3 we are left with two 1
by something rectangles plus one extra block. Here the something is the side of the
smaller rectangle. Thus we get S3 − S2 = 2 × 2 + 1 = 5. If we do this with squares
S16 and S15 we would get
S16 − S15 = 2 × 15 + 1 = 31 .
Quick, what is 1 + 3 + 5 + 7 + 9 + 11 + 13 + · · · + (2 + 1)? Working backwards we
see it is
(S16 − S15) + (S15 − S14) + · · · + (S2 − S1) + 1 = S16 = 16 × 16 = 256.
See the schematic picture below:
Figure 6: Sum of odds
Notice that this is
1 + 3 + 5 + · · · + (2 × 6 + 1) = 7 × 7 = 49 .
This last Figure shows that the difference of two squares of any size can be related
to a rectangle. In a formula one has
a2
− b2
= (a + b)(a − b) .
Thus 93 × 87 = 8100 − 9 = 8991.
5

6. Figure 7: Difference of squares version 2
(3) Let T5 also denote the number of squares in T5 . Then T2 − T1 = 2, T3 − T2 = 3,
and T16 − T15 = 16.
(4) Look at the number in the top row, then the second row, etc..
T15 = 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 + 13 + 14 + 15 .
Now look at the Figure below. It shows two copies of T3 fit together to make a
(3 + 1) × 3 rectangle. Thus 2T3 = (3 + 1) × 3 so T3 = 1
2(3 + 1) × 3 and
T15 =
1
2
(15 + 1) × 15 = 120 .
Figure 8: Two copies of a triangular number
(5) The two answers in the previous part must be the same. Thus
1+2+3+4+5+6+7+8+9+10+11+12+13+14 = T14 =
1
2
(14+1)×14 = 105 .
(6) The addition table from 0+0 up to 2+2 is displayed in Figure 9. The top two layers
form a tetrahedral configuration. It it is removed, it may be placed in the corner
that remains to complete a 3 × 3 × 2 brick. The analogous thing will happen with
the addition table from 0 + 0 up to 49 + 49. Namely, we move the top 49 layers to
fill in the corner to get a 50 × 50 × 49 brick. Thus there are 124, 750 blocks in the
3D addition table from 0 + 0 up to 49 + 49. Alternately, two copies of the addition
table may be put together to produce a 50 × 50 × (49 + 49) “brick.” The sum will
be one half the number of blocks in this brick.
(7) The elements in the third row are 2 + 0, 2 + 1, 2 + 2, . . . . Each step we take to the
right adds on to the answer. The same occurs in each row. Each step down a column
the answer will get one larger. Since we start the addition table at 0 + 0, the first
row is the 0+ row, the second row is the 1+ row, etc..
(8) We start the multiplicaiton table at 1 × 1. Thus the third row will be 3 × 1, 3 × 2,
3 × 3, . . . . If we stop at 3 × 5, this is just like the fifthe triangular number stretched
up by a factor of 3. Thus it gets 3 units larger each step we take to the right in the
6

7. Figure 9: Addition Table
third row. It gets 13 units larger each step we take to the right in the 13th row.
Similarly, it will get 3 units larger each step we tak down the third column.
(9) The third row from 3 × 1 to 3 × 7 will just be 3T7 .
(10) If we lay out the multiplication table as in Figure 3 we see that it fills up a square of
side 1+2+· · ·+29. This is just the 29th triangular number so T29 = 1
2(29+1)×29.
The number of little squares in this flat model would then be 1
2(29 + 1) × 29
2
.
(11) There are 12 layers of squares of side 12 in the cube of side 12. Each square of little
cubes contains 12 × 12 small cubes, so there are 12 × 12 × 12 small cubes in C12 .
This is why it is commonly called the 12 × 12 × 12 cube.
(12) Look at Figure 10. It shows a decomposition of a C3 into a C2 , three 1 × 2 × 2
bricks, three 1 × 1 × 2 bricks and a final C1 . The same thing will happen with C15 .
It may be decomposed into three 1 × 14 × 14 bricks, three 1 × 1 × 14 bricks and a
final C1 . Thus,
153
− 143
= 3 · 142
+ 3 · 14 + 1 .
(13) It is a triangular pattern of cubes. Thus Tet9 − Tet8 = T9 .
(14) It is natural to put three pyramids together. The left over bit will be a triangluar
number. It can be cut in half and moved to complete a brick as in Figure 11
(15) The sum 1 × 4 + 2 × 3 + 3 × 2 + 4 × 1 is the fourth tetrahedral number Tet4 . See
Figure 12.
(16) The tems in the third ell are 1 × 3, 2 × 3, 3 × 3 and 3 × 2 and 3 × 1. Notice that
1×3+2×3+3×3 = T3 ×3 and 3×2+3×1 = 3T2 . Thus the number of little cubes
over the third ell in the multiplication table is 3(T3 + T2) = 3 · 32 = 33 . Similarly,
the sum of the cubes over the fourth ell is 43 .
(17) By the answer to (10) it would just be the number of cubes in a model of the
multiplication table up to 7 × 7. Now the answer to (16) makes this
13
+ 23
+ 33
+ 43
+ 53
+ 63
+ 73
=
1
2
(7 + 1) × 7
2
.
Comments/Questions? Contacct: Dave Auckly Math Department Kansas State University
dav@ksu.edu
7

8. Figure 10: Difference of adjacent cubes
Mathematics Beneath & Beyond:
The problems in this session all fit under the category of “proof without words.” There
are many sources for such proofs. The books Proofs without Words: Exercises in Visual
Thinking (Classroom Resource Materials) (v. 1, 2, 3) by Roger Nelson is one source.
Proofs Without Words and Beyond - Proofs Without Words 2.0 by Doyle, e.al. is another.
Mathematics Magazine and the College Mathematics Journal each regularly include proof
without words.
A proof without words is similar to a bijective proof. In combinatorics the gold standard
is a bijective proof. In a bijective proof, one represents one expression as a formula that
counts something, and a expression as a formula that counts something else. If one can
describe a one-to-one and onto (bijective) corespondence between the two sets, the two
sides must be the same. To see an example, let n
k represent the number of ways to choose
k items from a set of n items. In this case 5
2 = 10 because the following are all ways of
choosing 2 elements from 5:
{1, 2}, {1, 3}, {1, 4}, {1, 5}, {2, 3}, {2, 4}, {2, 5}, {3, 4}, {3, 5}, {4, 5}.
We claim n
k = n
n−k . Indeed given any way to choose k elements from n, one may just
considet the set of elements that were not chosen. In the example we can associate the set
{3, 4, 5} to the set {1, 2}, etc..
There are many remarkable bijective proofs. One could even wildly suggest that any true
mathematical fact would have a bijective proof. Similarly, one could go wild and imagine
8

9. that it The Book has proofs without words for every true mathematical statement. Such
speculation is indeed wild, but is is fun to try to find such proofs.
The optional multiplication table construction is an example of a ruled surface. A ruled
surface is a surface that may be expressed as a union of straight lines. See for example,
Geometry and the Imagination (AMS Chelsea Publishing).
These notes lead to forumla for
1 + 2 + · · · + n =, 12
+ 22
+ · · · + n2
=, and 13
+ 23
+ · · · + n3
=, .
One may wonder if there is a closed formula for
1p
+ 2p
+ · · · np
.
The answer is yes. Here is a brief exposition that uses series manipulations:
The Bernoulli numbers defined as the coefficients of the exponential generating function
below,
z
ez − 1
=
∞
k=0
Bkzk
k!
.
Expand eNz−1
z
z
ez−1 as a sum of exponentials, and then expand the exponentials into power
series to obtian N + ∞
n=1
N−1
j=1 jp zn
n! .
Expand eNz−1
z and z
ez−1 into power series. Multiply the resulting series to get a series for
eNz−1
z
z
ez−1 . Compare this with the prior formula to obtain:
N−1
j=1
j2p+1
= −
N2p+1
2
+
p
k=0
2p + 1
2k
B2kN2p−2k+2
2p − 2k + 2
,
N−1
j=1
j2p
= −
N2p
2
+
p
k=0
2p + 1
2k
B2kN2p−2k+1
2p + 1
.
Presentation:
There are a number of optional bits that may be included in this presentation. We will
first describe one presentation for a fairly elementary audience, and then describe some of
the options at the end of the basic description.
Part 1: To begin have a counting race. Pick two participants and tell them that they are
going to race to count some number of cubes. Then put a disorganized heap in front of
one and an array in front of the other as in the following image:
9

10. Of course the student with the array should win. Ask why and have everyone understand
that it is easier to count items in an array.
After the race ask participants to make a model of (2 + 3)2 out of the blocks so that they
can see 22 and 32 . You are hoping someone will create a model that looks like the following
image:
Ask if (2 + 3)2 is equal to the sum of 22 and 32 . Write
(2 + 3)2
= 22
+ 32
+ 2 × (2 × 3)
where all can see it.
Draw a cartoon of the figure for (21 + 33)2 and discuss it.
Demonstrate the following multiplication trick: ask someone to tell you a two-digit number
that has a 5 in the ones place, e.g., 75. Tell them 75 × 75 = 5625. Repeat with a couple
more numbers. Then describe the following extimate: 75 is between 70 and 80, so it is
not unreasonable to guess that 75 × 75 is close to 70 × 80 = 5600. The trick is to multiply
the tens place with one more than the number in the tens place (so 7 × 8 in our example)
then append 25 hence 5625.
Ask for a pair of numbers that add to 55. Ask what “fifty five” means. (Answer: five
tens plus five.) Then partially cut a square piece of paper into a (30 + 5)2 configuration as
in the following image. Label the edges of the specific rectangles (perhaps draw the same
10

11. figure on the board.) Rip away the small square representing 5 × 5 = 25 then give the
rest of the paper to a participant and ask them to rearrange the paper recalling that it is
easier to compute the area of a rectangle. You should get a configuration like the one on
the right below.
Ask if the same trick would work for 24×28. Ask if a similar trick would work for 45×75.
Ask if a similar trick would work for 62 × 68. Ask them to justify any trick that works.
(The last trick will work using the same geometric reasoning as the 75 × 75 trick. An
algebraic deriviation is as follows:
(10n + k)(10n + {10 − n}) = 100n2
+ 10nk + 10n(10 − k) + k(10 − k)
= 100nn + 10n10 + k(10 − k) = 100n(n + 1) + k(10 − k) .
Part 1 could be optional, but it does lead to a nice conclusion at the end of the session.
Part 2: Ask the participants to make a model of 1 + 2 + 3 + 4 where they can see each
of the numbers. Have some of the students make the model out of all white blocks and
some make it out of all black blocks. Remind the students that it is easier to compute the
number of items in an array. The students might then be motivated to combine a white
model with a black model as in Figure 8.
Instead of combining two different models together, some participants may rearrange the
cubes in one model to make an array. The is more natural when CAT is an even number.
Otherwise, one would wish to cut the last column of blocks in half. After they get the first
sum ask for 1+2+· · ·+6+7. See if they can figure it out without making a model. Then
ask for 1 + 2 + · · · + 16 + 17, and 1 + 2 + · · · + 1000 and 1 + 2 + · · · + CAT . Ask them to
tell you the answer for each of the last three without simplifying any of the arithematic.
Thus the answers to two fo the last three problems will be:
17 × (17 + 1)
2
and
CAT × (CAT + 1)
2
.
[It is very beneficial to generalize up from small numbers to medium numbers where the
arithematic is still easy, then up to even larger numbers without doing the arithematic
11

12. and finally to general place holders. Doing so before studying algebra will make the ideas
easier. Doing so during the study of algebra will help people remember that letters represent
numbers.]
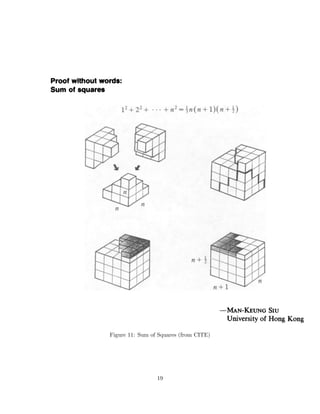
After students figure out the formula for the sum of the first so many positive integers
(such sums are called triangular numbers) they could move on to find the sum of the first
so many squares.
We slightly prefer asking them to build a model of the addition table. Give them a grid
as in the following image and ask them to build stacks up representing the values of the
sums. Their model will look thik the image on the right.
Once the students build a model for the addition table ask them to explain why some of
the stacks of blocks are the same height, e.g. 3 + 0 and 1 + 2. Ask why the model is
symmetric along the diagonal. Point out the triangular sections.
Ask them for the sum of the numbers in the addition table 0 + 0 up to 3 + 3. Then ask
for the sum of the numbers in the addition table 0 + 0 up to 13 + 13, and then 0 + 0 up
to CAT + CAT .
After they compute the sum of the sums in an addition table, ask the students to make
a model of the multiplication table 1 × 1 up to 3 × 3. It is possible to make the “big
city” model building up, or the checkerboard “farmland” model. The “farmland” model is
displayed in Figure ??. The “big city” model is one of the towers in the following image
of “Sauron’s tower.”
12

13. One nice option is to build a large base of “bedrock” before the session and dig out the
products representing ab with ab < 0. See the image below. Given such a model you can
have a participant build the “big city” model in the a > 0 and b > 0 quadrant. From
there they can think and fill in the a < 0 b < 0 quadrant.
This is a wonderful way to demonstrate that the product of a pair of negative
numbers is positive. Take time to explain it. Point out the 0 × n column and the
n × 0 row. Ask what happens to the product when one moves form 1 × 3 to 1 × 2 then
to 1 × 1. Note where it goes at 1 × (−1). Now look at 2 × 3, 2 × 2 and follow down to
2 × (−1). Compare 2 × (−1) to 1 × (−1) to 0 × (−1). What must (−1) × (−1) be? Build
the full “big city” multiplication table (−3) × (−3) to 3 × 3.
Ask the students to compute the sum of the entries in the multiplication table 1 × 1 up to
3 × 3. The “farmland” model will make it clear that the answer is (1 + 2 + 3)2 . Ask the
same thing for the multiplication table 1 × 1 up to 10 × 10. This time the answer will be
(1 + 2 + · · · + 10)2 = 10(10+1)
2
2
= 552 = 3025. This brings us back to where the session
began.
It may be that some participants sum the entries of the multiplication table by putting
several (four) together. This would be done by using a second table to complete the
“triangles” along the rows of the first multiplication table to get a triangular prism. Two
more multiplicatoin tables may be combined into a second prisim. The two prisims then
fit into a “brick.”
The entire presentation as described can work with a moderate to advanced group in one
90 minute session. For a more elementary group the same material may be divided into
two sessions.
At the end of the session give everyone a copy of the questions on the handout.
Options: There is an optional way to start the session, and three optional models one could
make. The first model to consider making is the base for the multiplication table. This
13

14. would be a 7 × 7 × 9 block of black cubes with the multiplication table removed from two
corners representing the negative products in the multiplicatoin table. The model may be
hollow. It should be glued together. This model was described in the sample presentation
that we gave. It is pictured below.
For the optional start, show the students a doubly-ruled hyperbolic paraboloid made from
cardboard and string, or make one from yarn, PVC pipe and fittings with the students.
The PVC model fits together fairly quickly and may be done at the start of the session.
The cardboard and string model takes long enough that the session would turn into an “art
class” if participants made the cardboard and string model. Thus, if you do elect to have
the students make individual cardboard and string models we recommend giving them the
materials and instruction page at the end of this script for them to make at home or in art
class.
To make the PVC model, have the hardware store cut two 1 inch sections off of each piece
and then cut each piece of pipe into two equal lengths (most hardware stores will od this
for free). At this point you will have four 1 inch sections and four long sections. The frame
is a rhombus partly folded along one diagonal. Put a long section of pipe into each opening
of the 90◦ fittings creating two V-shapes. Then make two “chains” consisting of 45◦ , 1
inch, 45◦ , 1 inch, 45◦ . These chains may be used to attach the two V-shapes together to
get the final frame.
From here tape yarn on top of the frame in the same pattern used to thread the string and
cardboard model. [Many wonderful mathematical models may be created out of PVC and
yarn.]
When you show the model, ask the participants if they know what it is. (It is unlikeley
that anyone will recognize it as the multiplication table.) Later after the participants
have constructed the “big city” multiplication table go back to the hyperbolic paraboloid.
Hole it so that two strings that cross lay in a horizontal plane. These strings represent
0 × y and x × 0. The entire structure is seen to be the graph of f(x, y) = xy, i.e. the
14

15. multiplication table. Strings make straight lines of various slopes with f(1, y) representing
multiplication by 1, described by the counting sequence; f(2, y) representing multiplicaiton
by 2, described by skip counting by 2s, etc..
We have not seen all of the problems on the hand out addressed in a single session. However,
every problem has been discussed in one of the sessions that we have given.
15

16. Hyperbolic Paraboloid Instructions
Step 1 Cut corner out of cardboard box.
Step 2 Draw an isosceles triangle with base on one of the edges where two faces of the
cardboard corner meet and put equidistributed marks (about 1/2 inch apart) on the
two equal lines. Use an odd number of marks on each line. Eleven marks works well.
Step 3 Poke holes at the marks using a nail. The lines with the marks form a 3-
dimensional shape that could be described as a rhombus folded partway along a
diagonal.
Step 4 Tie a knot in the end of a piece of string (100 inches long if you are going to use
two strings, 200 inches if you will use one), and thread the string through one of the
16

17. four holes furthest from an edge from the “outside” of the box to the “inside” of the
box.
Step 5 Now thread (“inside” to “outside”) the string through the hole in the edge of the
foleded rhombus that was parallel to the edge containing the first hole and closest to
the edge joining the two faces.
Step 6 Now thread the string through the next hole in the same edge.
Step 7 Continue to the second hole on the original line of holes. (This will be right next
to the first hole that you threaded.)
Continue in this way until all holes in the first pari of originally parallel lines are used.
17

18. Continue threading with the first hole on the two unused edges. (You may continue with
the same string, or start a new string of a different color. This time weave the string
through the existing strings. The end result will look like the following:
18

19. Figure 11: Sum of Squares (from CITE)
19

20. Figure 12: A diagonal slice of the multiplication table
20