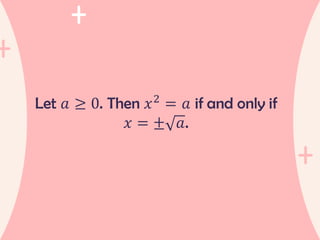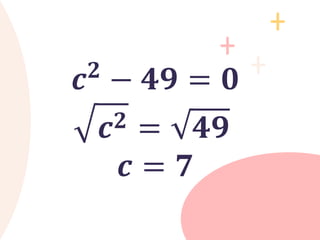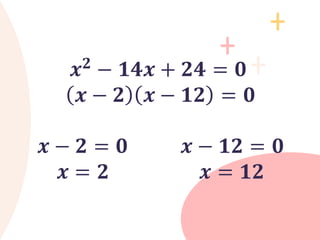The document provides an overview of quadratic equations, defining their standard form and differentiating them from linear equations. It explains methods for solving these equations, such as extracting square roots and factoring, with examples illustrating the application of these methods. Additionally, it includes practice problems and solutions for better understanding of quadratic equations.

1. MATHEMATICS 9
LESSON 1

2. SOLVING
QUADRATIC
EQUATIONS

3. ● A quadratic equation in one variable is an
equation of the form 𝑎𝑥2
+ 𝑏𝑥 + 𝑐 = 0,
where a, b, and c are real numbers and
𝑎 ≠ 0.
● Examples:
𝑥2
− 𝑥 + 7 = 0
3𝑥2
− 𝑥 = 0
−2𝑥2
+ 3 = 0
5𝑥2
+ 𝑥 − 3 = 0
● Such quadratic equations are said to be in
standard form.
Quadratic Equation
Defined

4. Linear equations
5𝑛 = 10
3 𝑥 + 2 = 14
5𝑦 − 2 = 13
3𝑎 + 4
2
= 1
𝑧 − 1 + 2 = 2𝑧
Quadratic equations
𝑛2
= 49
2𝑥2
− 3𝑥 = 12
4(𝑦 + 2)2
= 27
𝑎2
+ 3
2
= 7
(𝑧 − 3)2
= 3 − 𝑧
Here are some more examples of linear
equations and quadratic equations …

5. Solving Quadratic
Equations by Extracting
the Square Root

6. Let 𝑎 ≥ 0. Then 𝑥2
= 𝑎 if and only if
𝑥 = ± 𝑎.

7. The following quadratic
equations can be solved by
extracting the square roots.

8. 𝑥2
− 121 = 0
𝑥2
= 121 Addition Property of Equality
𝑥 = ±11 121 = 11
Example #1

9. 3𝑥2
− 27 = 0
3𝑥2
= 27 Addition Property of Equality
𝑥2
= 9 Multiplication Property of Equality
𝑥 = ±3 9 = 3
Example #2

10. 5𝑥2
− 125 = 0
5𝑥2
= 125
𝑥2
= 25
𝑥 = ±5
Example #3

11. 𝑥2
= 15
𝑥 = ± 15
Example #4

12. Solving Quadratic
Equations by
Factoring

13. If the area of the rectangular garden is
84𝑚2
and its perimeter is 38m, what
are the dimensions of the garden?

14. The area of the rectangular garden can
be expressed as 𝑙𝑒𝑛𝑔𝑡ℎ × 𝑤𝑖𝑑𝑡ℎ = 84
and its perimeter can be expressed as
2 𝑙𝑒𝑛𝑔𝑡ℎ + 2(𝑤𝑖𝑑𝑡ℎ) = 38 or
𝑙𝑒𝑛𝑔𝑡ℎ + 𝑤𝑖𝑑𝑡ℎ = 19.

15. To solve the problem, we let 𝑥 be the width.
Then, length = 19 − 𝑥. Since 84 = 𝑙𝑒𝑛𝑔𝑡ℎ ×
𝑤𝑖𝑑𝑡ℎ, we now have the equation
84 = 19 − 𝑥 𝑥 Substitution
84 = 19𝑥 − 𝑥2
Distributive Property
𝑥2
− 19𝑥 + 84 = 0 Transform into standard form

16. We can factor 𝑥2
− 19𝑥 + 84 into 𝑥 − 7 𝑥 − 12 ,
and proceed to solve for 𝑥.
𝑥 − 7 𝑥 − 12 = 0
𝑥 − 7 = 0 or 𝑥 − 12 = 0 Zero-Product Property
𝑥 = 7 𝑥 = 12
If 𝑥 = 7, then 19 − 𝑥 = 12. If 𝑥 = 12, then 19 − 𝑥 = 7.
Both of the cases give the same dimensions. Therefore,
the dimensions of the garden are 7𝑚 and 12 𝑚.

17. Zero-Product Property
For any real numbers a and b, ab = 0 if
and only if a = 0 or b = 0.

18. The following quadratic
equations can be solved by
factoring.

19. 𝑥2
− 6𝑥 = −8
Solution: Make sure one side of the equation is 0 before
applying the zero-product property.
𝑥2
− 6𝑥 = −8 transform into standard form
(𝑥 − 4)(𝑥 − 2) = 0 factor the left side
𝑥 − 4 = 0 𝑜𝑟 𝑥 − 2 = 0 Zero-Product Property
𝑥 = 4 𝑥 = 2 Solve for x
Check:
At 𝑥 = 4: At 𝑥 = 2:
(4)2
−6 4 = −8 (2)2
−6 2 = −8
16 − 24 = −8 4 − 12 = −8
−8 = −8 −8 = −8
Example #1

20. (𝑥 + 2)2= 9
Solution:
𝑥2
+ 4𝑥 + 4 = 9 Square the binomial
𝑥2 + 4𝑥 − 5 = 0 Transform into standard form
(𝑥 + 5)(𝑥 − 1) = 0 Factor the left side
𝑥 + 5 = 0 𝑜𝑟 𝑥 − 1 = 0 Zero-Product Property
𝑥 = −5 𝑥 = 1 Solve for x
Check:
At 𝑥 = −5: At 𝑥 = 1:
(−5 + 2)2= 9 (1 + 2)2= 9
(−3)2= 9 (3)2= 9
9 = 9 9 = 9
Example #2

21. PRACTICE!

22. 1. 𝑐2 − 49 = 0
2. 𝑥2 − 14𝑥 + 24 = 0
Solve the following
quadratic equations.

23. 𝒄𝟐
− 𝟒𝟗 = 𝟎
𝒄𝟐 = 𝟒𝟗
𝒄 = 𝟕

24. 𝒙𝟐 − 𝟏𝟒𝒙 + 𝟐𝟒 = 𝟎
𝒙 − 𝟐 𝒙 − 𝟏𝟐 = 𝟎
𝒙 − 𝟐 = 𝟎 𝒙 − 𝟏𝟐 = 𝟎
𝒙 = 𝟐 𝒙 = 𝟏𝟐