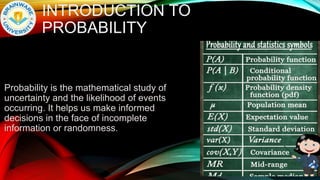
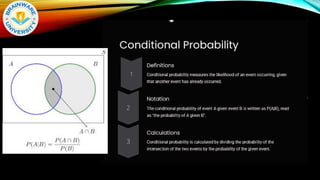
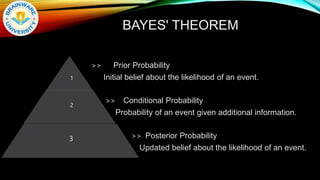
The document provides an overview of probability and statistics, covering key concepts such as sample spaces, events, probability axioms, and conditional probability. It explains independent and dependent events, along with Bayes' theorem, which is crucial for updating probabilities based on new information. The document also introduces discrete and continuous probability distributions, focusing on their applications in various fields.

1. STUDENT DETAILS
• Name - Devraj Maji
• Name of Department - Department of Computer science and Engineering
• Program Name - B. Tech. CSE(AIML)2024
• Semester/Year - 2nd semester/1st Year
• Crouse Code - BSCM202
• Course Name - Probability & Statistics
• Student Code - BWU/BTA/23/428
• Section - H

2. CONTENTS
1. Introduction to Probability
2. Sample Spaces and Events
3. Probability Axioms and Rules
4. Conditional probability
5. Independence and Dependence
6. Bayes' Theorem
7. Discrete Probability Distributions
8. Continuous Probability Distributions

3. INTRODUCTION TO
PROBABILITY
Probability is the mathematical study of
uncertainty and the likelihood of events
occurring. It helps us make informed
decisions in the face of incomplete
information or randomness.

4. DEFINITIONS AND TERMINOLOGY
• Sample Space: The set of all possible outcomes in a probability experiment.
• Event: A subset of the sample space that we are interested in observing or
measuring.
• Probability: A numerical measure of the likelihood that an event will occur,
expressed as a value between 0 and 1.

5. SAMPLE SPACES AND EVENTS
• A sample space is the set of all
possible outcomes of an
experiment. Events are subsets of
the sample space, representing
specific outcomes of interest.
• Understanding sample spaces and
events is fundamental to
probability theory, enabling us to
precisely define and analyze the
likelihood of different outcomes.

6. PROBABILITY AXIOMS AND RULES
• Axiom 1: Non-Negativity
--->> The probability of any event must be a
non-negative number, meaning it cannot be less than
zero.
• Axiom 2: Certainty
--->> The probability of the entire sample space,
or the certain event, is equal to 1.
• Axiom 3: Additivity
--->> The probability of the union of two
mutually exclusive events is the sum of their individual
probabilities.

8. INDEPENDENCE AND
DEPENDENCE
Independence
Events are
independent if the
occurrence of one
event does not
affect the probability
of the other event.
Independent events
have no influence
on each other.
Dependence
Dependent events
are those where the
outcome of one event
affects the probability
of the other event.
The occurrence of
one event changes
the likelihood of the
other event.
Conditional
Probability
The probability of an
event given that
another event has
occurred is called
conditional
probability. It
describes the
likelihood of one
event happening
given the occurrence
of another event.
Examples
Flipping a fair coin
twice is an example of
independent events.
Drawing a card from a
deck and then drawing
another card is an
example of dependent
events.

9. BAYES' THEOREM
1
2
>> Prior Probability
Initial belief about the likelihood of an event.
>> Conditional Probability
Probability of an event given additional information.
>> Posterior Probability
Updated belief about the likelihood of an event.
3

10. BAYES' THEOREM
DEFINATION>> Bayes' Theorem
is a fundamental concept in probability
theory that describes the relationship
between conditional probabilities. It
allows us to update our beliefs about
the likelihood of an event based on new
information. This powerful statistical
tool has applications in fields like
machine learning, medical diagnosis,
and decision-making.

11. DISCRETE PROBABILITY
DISTRIBUTIONS
Binomial Distribution
Describes the probability of a fixed
number of successes in a series of
independent Bernoulli trials. Useful for
modeling events with two possible
outcomes, like coin flips or product
defects
Models the probability of a given number of
events occurring in a fixed interval of time or
space, assuming these events happen with
a known rate and independently of the time
since the last event.
Poisson Distribution

12. CONTINUOUS PROBABILITY DISTRIBUTIONS