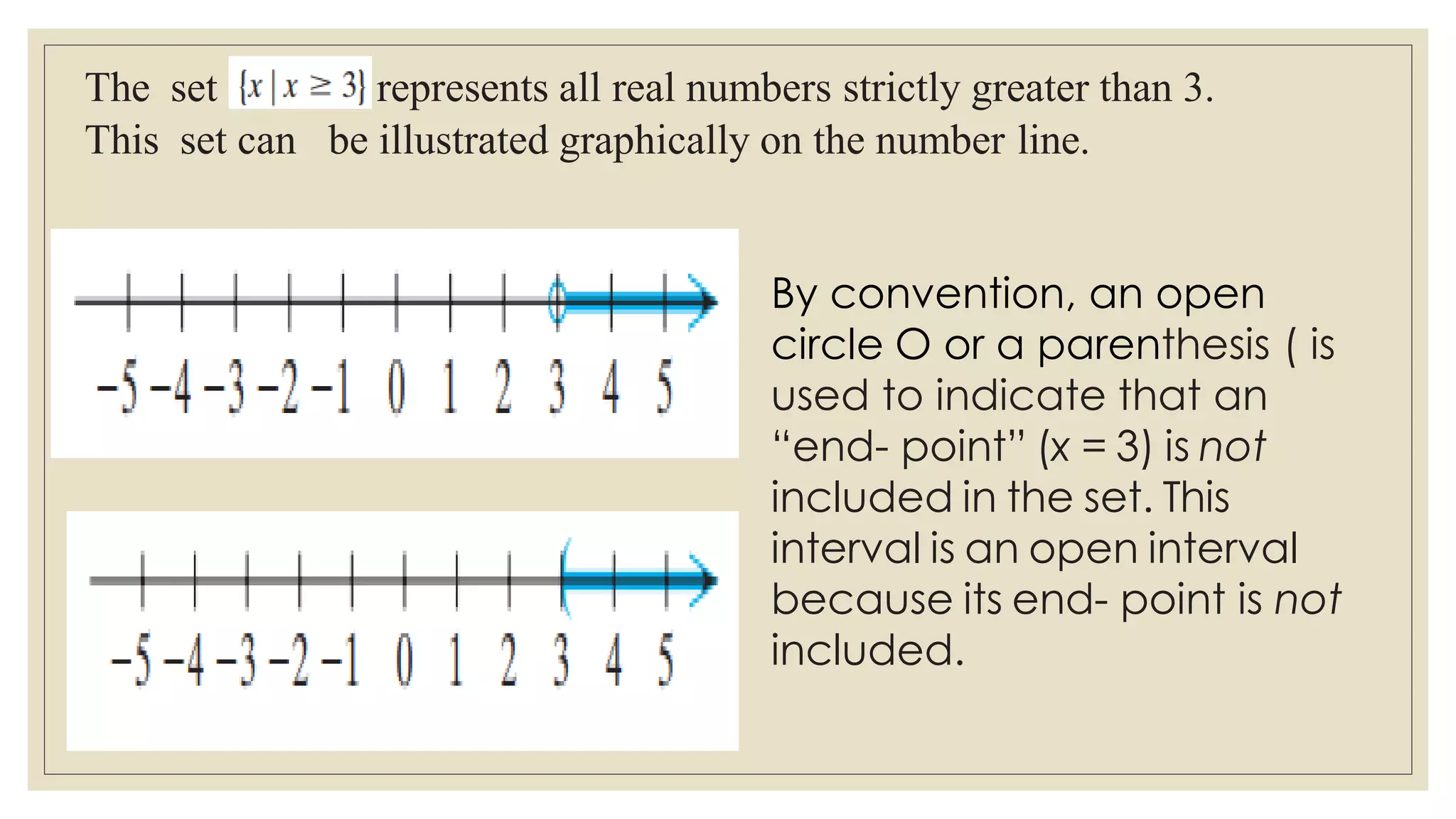
This document discusses inequalities and interval notation in abstract algebra. It defines less than (<) and greater than (>) symbols to compare real numbers on a number line. Interval notation uses brackets [ ] or parentheses ( ) to indicate if endpoints are included or excluded from sets of real numbers. For example, the set of real numbers greater than or equal to 3 can be written as the closed interval [3, ∞). The document provides examples of writing set-builder and interval notations to represent sets of real numbers on a number line.

1. MATH 11
ABSTRACT ALGEBRA
Lesson 2

2. 2. Inequalities
The relative size of two numbers can be compared by using the
real number line. We say that a is less than b (written
mathematically as a < b) if a lies to the left of b on the number
line.
We say that a is greater than b (written mathematically as a >b) if
a lies to the right of b on the number line.

3. Table 1-1 summarizes the relational operators that compare two real numbers a
and b.

4. REMEMBER:
The symbols <, >, ≥ , ≤, and ≠ are
called inequality signs, and the
expressions a<b, a>b, a ≤ b, a ≥ b, and
a ≠ b are inequalities

5. Sample Practice
Ordering Real Numbers
Fill in the blank with the appropriate inequality symbol: > or <
a. -2 ____ -5
b. .
c. -1.3 _____ 2.8

6. Check your answer

7. Fill in the blanks with the appropriate symbol, < or > .

8. 3. Interval Notation
The set and represents all real numbers greater
than or equal to 3. This set can be illustrated graphically on the
number line.
By convention, a closed
circle ● or a square
bracket [ is used to indicate
that an “end- point” (x = 3) is
included in the set. This
interval is a closed interval
because its endpoint is
included

9. The set represents all real numbers strictly greater than 3.
This set can be illustrated graphically on the number line.
By convention, an open
circle O or a parenthesis ( is
used to indicate that an
“end- point” (x = 3) is not
included in the set. This
interval is an open interval
because its end- point is not
included.

10. Notice that the sets and consist of an infinite
number of elements that cannot all be listed.
Another method to represent the elements of such sets is by
using interval notation.
To understand interval notation, first consider the real number
line, which extends infinitely far to the left and right. The
symbol ∞ is used to represent infinity. The symbol -∞ is used
to represent negative infinity.

11. Remember This .!!!!!!!
To express a set of real numbers in interval notation, sketch the
graph first, using the symbols ( ) or [ ]. Then use these symbols at the
endpoints to define the interval.
Example:
Graph the sets on the number line, and express the set in
interval notation.
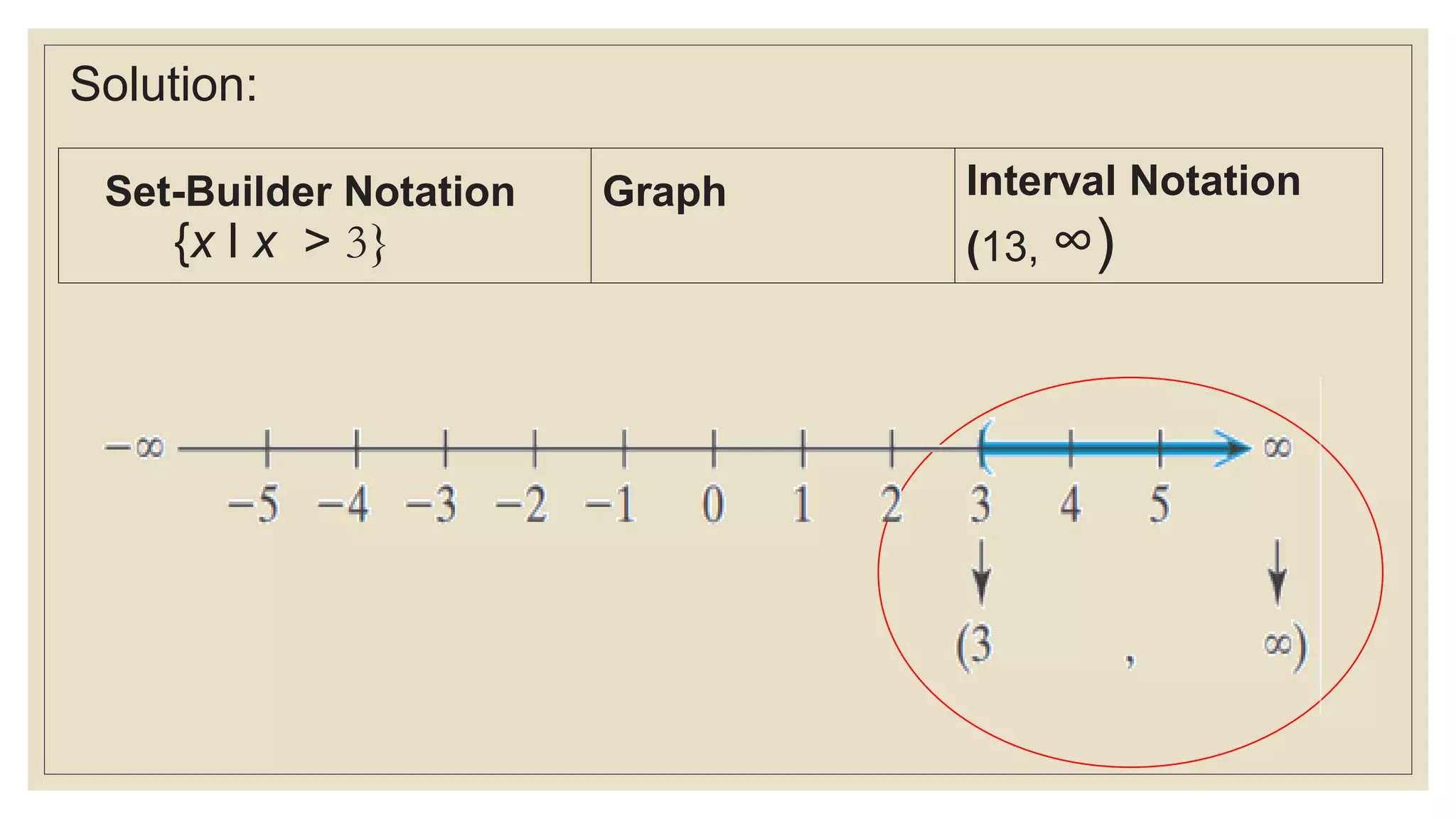
a. {x l x ≥ 3}
b. {x l x > 3}
c. {x l x ≤ - 3/2 }

12. Solution:
Set-Builder Notation Graph Interval Notation
[3, ∞)
The graph of the set {x l x ≥ 3} “begins” at 3 and extends infinitely far
to the right. The corresponding interval notation “begins” at 3 and
extends to ∞ . Notice that a square bracket [ is used at 3 for both the
graph and the interval notation to include x = 3. A parenthesis is
always used at ∞ (and at - ∞) because there is no endpoint.
{x l x ≥ 3}

13. Solution:
Set-Builder Notation Graph Interval Notation
(13, ∞)
{x l x > 3}

14. Solution:
Set-Builder Notation
Graph
Interval Notation
The graph of the set extends infinitely far to the left.
Interval notation is always written from left to right. Therefore, is
written first, followed by a comma, and then followed by the right-
hand endpoint.

15. Table 1-2 summarizes the solution sets for four general inequalities

16. POINTS TO REMEMBER!!!
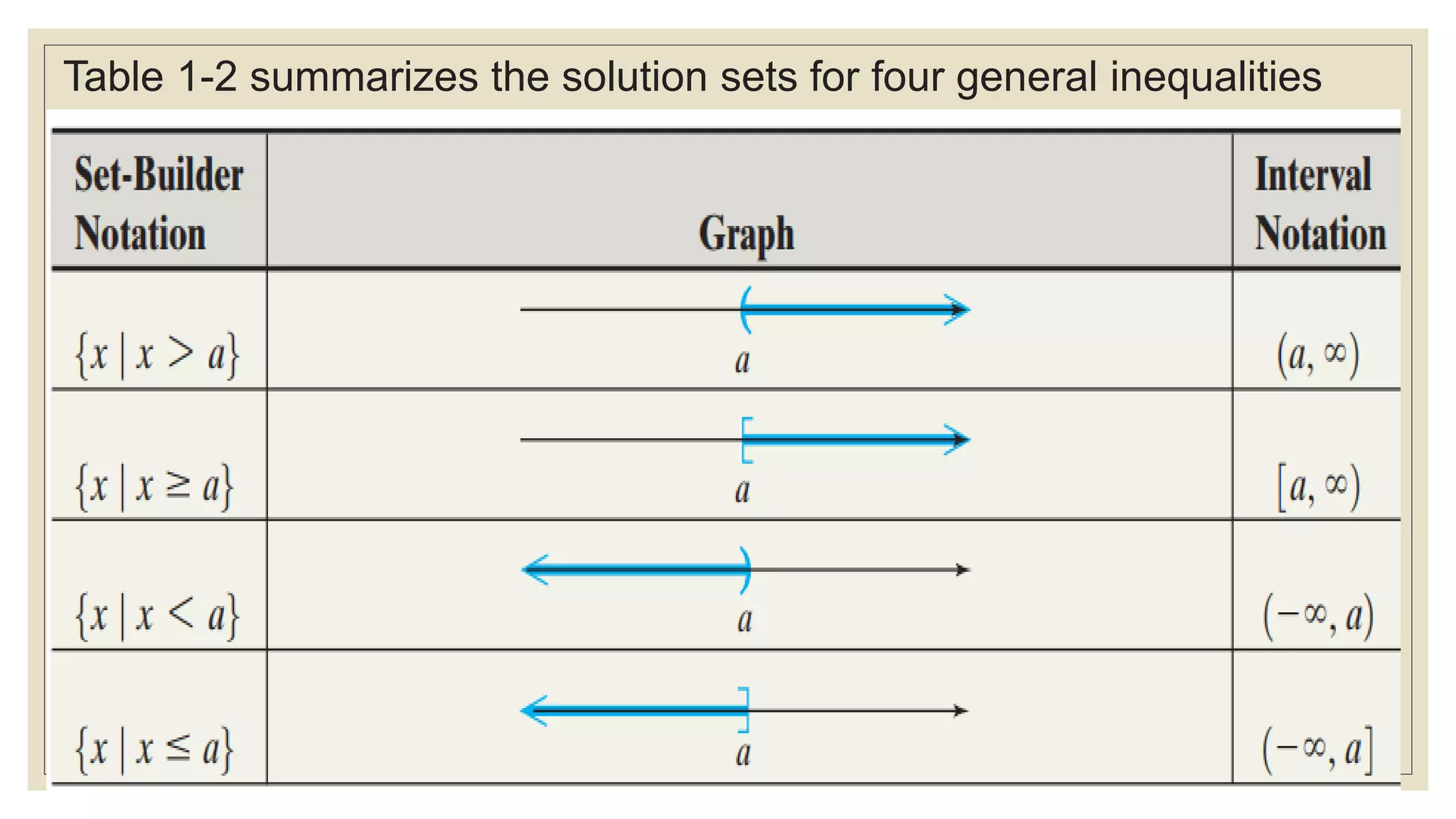
Using Interval Notation
• The endpoints used in interval notation are always written
from left to right. That is, the smaller number is written first,
followed by a comma, followed by the larger number.
• Parentheses ) or ( indicate that an endpoint is excluded
from the set.
• Square brackets ] or [ indicate that an endpoint is included
in the set.
• Parentheses are always used with ∞ and -∞ .

17. .
1. { w l w ≥ -7}
2. { x l x < 0}
3. { y l y > 3.5}
SKILL PRACTICE 2:
Graph and express the set, using interval notation.