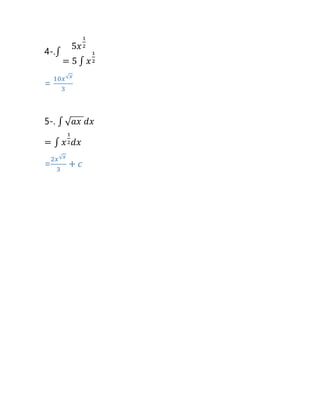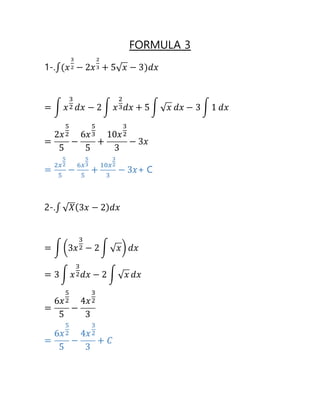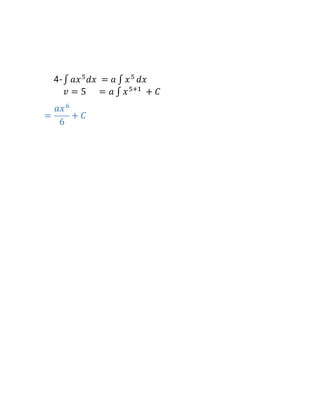CALCULO INTEGRAL

2. FORMULA 1
1-.∫(2𝑥3
− 5𝑥2
− 3𝑥 + 4)𝑑𝑥 =
= 2 ∫ 𝑥3
𝑑𝑥 − 5 ∫ 𝑥2
𝑑𝑥 − 3 ∫ 𝑥𝑑𝑥 + 4 ∫ 𝑑𝑥
=
𝑥4
2
−
5𝑥3
3
−
3𝑥2
2
+ 4𝑥 + 𝑐
2-.∫(𝑥4
)𝑑𝑥 =
=
𝑥5
5
+ 𝑐
3-.∫(3𝑥2
+ 4𝑥)𝑑𝑥 =
= 3 ∫ 𝑥2
𝑑𝑥 + 4 ∫ 𝑥𝑑𝑥
=
3𝑥3
3
+
4𝑥2
2
= 𝑥3
+ 2𝑥2
+ 𝑐
4-.∫(𝑥2
+ 𝑥)𝑑𝑥
= ∫ 𝑥2
𝑑𝑥 + ∫ 𝑥𝑑𝑥
=
𝑥3
3
+
𝑥2
2
+ 𝑐
5-.∫(7𝑥5
+ 9𝑥6
)𝑑𝑥
= 7 ∫ 𝑥5
𝑑𝑥 + 9 ∫ 𝑥6
𝑑𝑥

3. =
7𝑥6
6
+
9𝑥7
7
+ 𝑐

4. FORMULA 2
1-. ∫ 𝑥4
𝑑𝑥
= ∫
𝑥4+1
4+1
dx
=
𝑥5
5
+c
2-.∫ (𝑥
3
2 − 2𝑥
2
3 + 5𝑥√ 𝑥
− 3) 𝑑𝑥
= ∫ 𝑥
3
2 − ∫ 2𝑥
2
3 + ∫ 5 𝑥
1
2 − 3
2𝑥 √ 𝑥
2
−6 √ 𝑥23
5
=
10𝑥√ 𝑥
3
− 3𝑥 + 𝑐
3-.∫ 𝑥
2/3
𝑑𝑥
= ∫
𝑥
2
3
+1
2
3
+1
= ∫
𝑥
5
3
5
3
=
3𝑥 √ 𝑥23
5
+ 𝑐

5. 4-.∫
5𝑥
1
2
= 5 ∫ 𝑥
1
2
=
10𝑥√ 𝑥
3
5-. ∫ √ 𝑎𝑥 𝑑𝑥
= ∫ 𝑥
1
2 𝑑𝑥
=
2𝑥√ 𝑥
3
+ 𝑐

6. FORMULA 3
1-.∫(𝑥
3
2 − 2𝑥
2
3 + 5√ 𝑥 − 3)𝑑𝑥
= ∫ 𝑥
3
2 𝑑𝑥 − 2 ∫ 𝑥
2
3 𝑑𝑥 + 5 ∫ √ 𝑥 𝑑𝑥 − 3 ∫ 1 𝑑𝑥
=
2𝑥
5
2
5
−
6𝑥
5
3
5
+
10𝑥
3
2
3
− 3𝑥
=
2𝑥
5
2
5
−
6𝑥
5
3
5
+
10𝑥
3
2
3
− 3𝑥+ C
2-.∫ √ 𝑋(3𝑥 − 2) 𝑑𝑥
= ∫ (3𝑥
3
2 − 2 ∫ √ 𝑥) 𝑑𝑥
= 3 ∫ 𝑥
3
2 𝑑𝑥 − 2 ∫ √ 𝑥 𝑑𝑥
=
6𝑥
5
2
5
−
4𝑥
3
2
3
=
6𝑥
5
2
5
−
4𝑥
3
2
3
+ 𝐶

7. 3-.∫ 𝑦 ( 𝑎 − 𝑏𝑥2) 𝑑𝑥
= 𝑎𝑦 ∫ 1 𝑑𝑥 − 𝑏𝑦 ∫ 𝑥2
𝑑𝑥
= 𝑎𝑦𝑥 −
𝑏𝑦𝑥3
3
= 𝑎𝑦𝑥 −
𝑏𝑦𝑥3
3
+ 𝐶
4-.∫
4𝑥2
−2√ 𝑥
𝑥
𝑑𝑥
= ∫ (4𝑥 −
2
√ 𝑥
) 𝑑𝑥
= 4 ∫ 𝑥𝑑𝑥 − 2 ∫
1
√ 𝑥
𝑑𝑥
= 2𝑥2
− 4√ 𝑥
= 2𝑥2
− 4√ 𝑥 + 𝐶
5-.∫ 𝑥(2𝑥 + 1)1
𝑑𝑥

8. = ∫( 𝑢 − 1) 𝑢2
− 𝑑𝑢
= ∫( 𝑢3
− 𝑢2) 𝑑𝑢
= ∫ 𝑢3
𝑑𝑢 − ∫ 𝑢2
𝑑𝑢
=
(2𝑥 − 1)4
16
−
(2𝑥 + 1)3
12
=
(2𝑥−1)4
16
−
(2𝑥+1)3
12
+ C

9. FORMULA 4
1-∫ √ 𝑥 𝑑𝑥 = ∫ 𝑥1/2
𝑑𝑥
𝑉 = 1/2 =
𝑋3/2
3/2
+ 𝐶
=
2
3
𝑋3/2
+ 𝐶
2-∫
𝑑𝑥
𝑥3
= ∫ 𝑥−3
𝑑𝑥
𝑉 = 3 =
𝑥−2
−2
+ 𝐶
= −
1
2𝑥2
+ 𝐶
∫ 𝑋6
𝑑𝑥 = ∫ 𝑥6
𝑑𝑥
3- 𝑣 = 6 =
𝑥6+1
6+1
+ 𝐶
=
𝑋7
7
+ 𝐶

10. 4-∫ 𝑎𝑥5
𝑑𝑥 = 𝑎 ∫ 𝑥5
𝑑𝑥
𝑣 = 5 = 𝑎 ∫ 𝑥5+1
+ 𝐶
=
𝑎𝑥6
6
+ 𝐶

11. FORMULA 5
1. ∫ 𝑥4
𝑑𝑥
=
𝑥4+1
4+1
=
𝑥5
5
+ C
2. ∫
𝑑𝑥
𝑥2
=∫ 𝑥−2
dx
=
𝑥−1
−1
=
1
𝑥
+ C
3. ∫ 𝑥2/3
dx
=
𝑥
2
3
+1
2
3
+1
=
𝑥5
3
5
3
=
𝑥 5−3
1
5
3
=
3𝑥 5/3
5
+C

12. 4. ∫
𝑑𝑥
√ 𝑋
= ∫
𝑑𝑥
𝑥
1
2
= ∫ 𝑥−1/2
dx
=
𝑥1/2
1/2
=
𝑥1/2
1
1
2
=
2𝑥 1/2
1
=2√ 𝑥 + c
5. ∫
𝑑𝑥
3√ 𝑥
=
𝑑𝑥
𝑥
1
3
=∫ 𝑥−
1
3dx
=
𝑥
2
3
2
3
=
𝑥2/3
1
2
3
=
3𝑥43
2
+ c

13. FORMULA 6
1. ∫
𝑥3
𝑑𝑥
𝑥+1
=x-
𝑥2
2
+
𝑥3
3
− 𝐼𝑛( 𝑥 + 1) + 𝑐
2. ∫
2𝑥+1
2𝑥+3
𝑑𝑥
=x-In(2x+3)2
+ 𝑐
3. ∫
𝑥2 𝑑𝑥
2+3𝑥
=
𝐼𝑛(2+3𝑥)
3
+ 𝑐
4. ∫
𝑥2
𝑑𝑥
2+3𝑥
=
𝐼𝑛(2+𝑥3
3
+ 𝑐
5. ∫
𝑡𝑑𝑡
𝑎+𝑏𝑡2
=
𝐼𝑛(𝑎+𝑏𝑡2
2𝑏
+ 𝑐