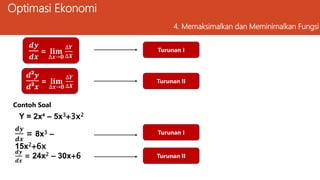
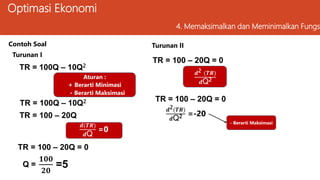
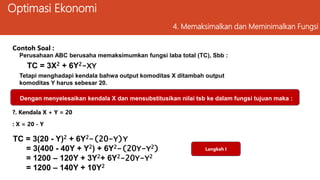
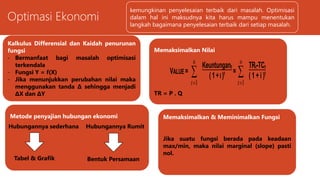
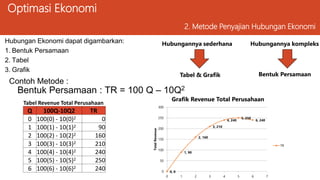
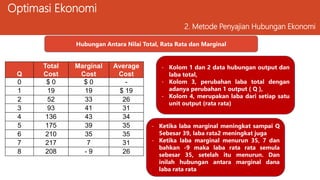
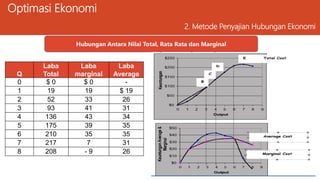
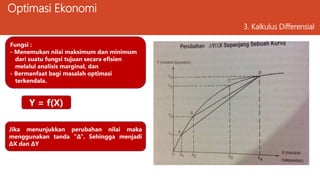
Dokumen ini membahas ekonomi manajerial dan teknik optimasi untuk memaksimalkan laba perusahaan serta meminimalkan biaya dengan berbagai metode analisis seperti kalkulus differensial dan penggambaran hubungan ekonomi. Selain itu, dijelaskan tentang kendala yang dihadapi dalam pengambilan keputusan manajerial dan contoh perhitungan optimasi dari fungsi laba. Keseluruhan materi bertujuan untuk membantu perusahaan menemukan solusi terbaik melalui pendekatan analitis.

1. Managerial Economics
“Optimasi Ekonomi”
Arsyad, lincolin. (2016). Ekonomi Manajerial (Ekonomi Mikro Terapan
Untuk Manajemen Bisnis). Edisi 4. Yogyakarta : BPFE-Yogyakarta
Deri Alan Kurniawan, S.E., MM
Universitas Garut

2. Pendahuluan
Ekonomi Manajerial sebagai penerapan teori ekonomi dan ilmu
pengambilan keputusan untuk mempelajari bagaimana suatu
perusahaan dapat mencapai tujuan dengan cara yang efisien.
 Tujuan: Maksimisasi laba/nilai perusahaan atau meminimumkan
biaya dengan kendala tertentu
Memberikan altenatif pemecahan (solusi)
terbaik bagi masalah yang dihadapi.
TEKNIK OPTIMASI
Metode untuk memaksimumkan atau meminimumkan fungsi
tujuan perusahaan
Max profit dengan kendala laba rugi
Max manfaat dengan minim fasilitas
Min kerugiaan dengan tingginya biaya
Min kegagalan produksi dengan minimnya
sarana

3. Optimasi Ekonomi
1. Memaksimalkan nilai perusahaan
2. Metode penyajian hubungan ekonomi
3. Kalkulus differensial dan kaidah kaidah
penurunan fungsi
4. Memaksimalkan dan meminimalkan fungsi
kemungkinan penyelesaian terbaik dari masalah. Optimisasi
dalam hal ini maksudnya kita harus mampu menentukan
langkah bagaimana penyelesaian terbaik dari setiap masalah.
Memaksimalkan Nilai
TR = P . Q
VALUE = 

n
t 1
Keuntungant
(1+I )t = 

n
t 1
TRt-TCt
( 1 + i )t
Metode penyajian hubungan ekonomi
Hubungannya sederhana
Tabel & Grafik
Hubungannya Rumit
Bentuk Persamaan
Kalkulus Differensial dan Kaidah penurunan
fungsi
- Bermanfaat bagi masalah optimisasi
terkendala
- Fungsi Y = f(X)
- Jika menunjukkan perubahan nilai maka
menggunakan tanda Δ sehingga menjadi
ΔX dan ΔY
Memaksimalkan & Meminimalkan Fungsi
Jika suatu fungsi berada pada keadaan
max/min, maka nilai marginal (slope) pasti
nol.

4. Optimasi Ekonomi
1. Memaksimalkan Nilai Perusahaan
VALUE = 

n
t 1
Keuntungant
( 1 + I )t = 

n
t 1
TRt-TCt
( 1 + i )t TR = P . Q
Faktor Faktor dari TR (Total Revenue) perlu
diperhatikan dalam pembuatan keputusan
manajerial seperti pemilihan produk yang
dirancang, pengolahan, penjualan, strategi
periklanan, kebijakan harga, perekonomian yang
dihadapi, serta persaingan.
Analisis biaya (TC = Total Cost) memerlukan
penelaahan sistem produksi alternatif, pemilihan
teknologi, serta input yang digunakan.
Sehingga antara biaya dengan sumber keuangan akan
memengaruhi tingkat diskonto ( i ) yang digunakan
untuk menetapkan nilai perusahaan.

5. Terdapat kompleksitas dalam analisis pengambilan keputusan yang menjadi kendala dalam
penerapan pembuatan keputusan, sehingga untuk keputusan sehari hari, teknik optimasi
parsial yang sering digunakan. Pada optimasi parsial proses pengambilan keputusan hanya
memusatkan pada tujuan tujuan terbatas di dalam berbagai departemen di perusahaan.
Tindakan tindakan yang perlu diambil oleh pimpinan :
1. Menyajikan hubungan ekonomi dalam suatu bentuk yang dapat dianalisis, dan
2. Penerapan teknik untuk menetapkan/ menentukan penyelesaian yang optimal.
Memaksimalkan Nilai Perusahaan

6. Optimasi Ekonomi
2. Metode Penyajian Hubungan Ekonomi
Hubungan Ekonomi dapat digambarkan:
1. Bentuk Persamaan
2. Tabel
3. Grafik
Hubungannya sederhana Hubungannya kompleks
Tabel & Grafik Bentuk Persamaan
Contoh Metode :
Bentuk Persamaan : TR = 100 Q – 10Q2
Tabel Revenue Total Perusahaan
Q 100Q-10Q2 TR
0 100(0) - 10(0)2 0
1 100(1) - 10(1)2 90
2 100(2) - 10(2)2 160
3 100(3) - 10(3)2 210
4 100(4) - 10(4)2 240
5 100(5) - 10(5)2 250
6 100(6) - 10(6)2 240 0, 0
1, 90
2, 160
3, 210
4, 240
5, 250
6, 240
0
50
100
150
200
250
300
0 1 2 3 4 5 6 7
Total
Revenue
Grafik Revenue Total Perusahaan
TR

7. Optimasi Ekonomi
2. Metode Penyajian Hubungan Ekonomi
Hubungan Antara Nilai Total, Rata Rata dan Marginal
Hubungan Marginal didefiniskan sebagai
perubahaan variabel dependen dari suatu fungsi
yang disebabkan oleh perubahan salah satu
variabel independen sebesar satu unit.
Secara khusus menganalisis suatu fungsi tujuan
dengan melihat perubahan berbagai variabel
independen yang memiliki pengaruh pada
variabel dependen.
Term Biaya
TC Total Cost Total Biaya
AC Average Cost Biaya rata2
MC Marginal Cost Biaya Marginal
Term Penerimaan
TR Total Revenue Penerimaan Total
AR Average Revenue Penerimaan Rata-rata
MR Marginal Revenue Penerimaan Marginal

8. Optimasi Ekonomi
2. Metode Penyajian Hubungan Ekonomi
Hubungan Antara Nilai Total, Rata Rata dan Marginal
Q
Total
Cost
Marginal
Cost
Average
Cost
0 $ 0 $ 0 -
1 19 19 $ 19
2 52 33 26
3 93 41 31
4 136 43 34
5 175 39 35
6 210 35 35
7 217 7 31
8 208 - 9 26
- Kolom 1 dan 2 data hubungan output dan
laba total,
- Kolom 3, perubahan laba total dengan
adanya perubahan 1 output ( Q ),
- Kolom 4, merupakan laba dari setiap satu
unit output (rata rata)
- Ketika laba marginal meningkat sampai Q
5ebesar 39, laba rata2 meningkat juga
- Ketika laba marginal menurun 35, 7 dan
bahkan -9 maka laba rata rata semula
sebesar 35, setelah itu menurun. Dan
inilah hubungan antara marginal dana
laba rata rata

9. Optimasi Ekonomi
2. Metode Penyajian Hubungan Ekonomi
Hubungan Antara Nilai Total, Rata Rata dan Marginal
Q
Laba
Total
Laba
marginal
Laba
Average
0 $ 0 $ 0 -
1 19 19 $ 19
2 52 33 26
3 93 41 31
4 136 43 34
5 175 39 35
6 210 35 35
7 217 7 31
8 208 - 9 26

10. Optimasi Ekonomi
3. Kalkulus Differensial
Fungsi :
- Menemukan nilai maksimum dan minimum
dari suatu fungsi tujuan secara efisien
melalui analisis marginal, dan
- Bermanfaat bagi masalah optimasi
terkendala.
Y = f(X)
Jika menunjukkan perubahan nilai maka
menggunakan tanda “Δ”. Sehingga menjadi
ΔX dan ΔY

11. Optimasi Ekonomi
3. Kalkulus Differensial
𝒅𝒚
𝒅𝒙
= 𝐥𝐢𝐦
∆𝒙→𝟎
∆𝒀
∆𝑿
Turunan Y pada X sama
dengan limit dari ΔY/ΔX
Jika X mendekati 0
Konsep turunan sebagai
limit dari suatu rasio
adalah sama dengan slope
dari sebuah kurva.
Slope adalah suatu ukuran kemiringan dari sebuah garis, dan didefinisikan
sebagai tingginya kenaikan / penurunan per unit sepanjang sumbu horizontal.
Misalkan, variabel dependen (Y) adalah TR (Total
Revenue) dan Variabel Independen (X) adalah output
didefiniskan Marginal Revenue.
Jika X mendekati 0, maka perbandingan ΔY/ΔX sama
dengan slope dari sebuah garis pada kurva D.

12. Optimasi Ekonomi
3. Kaidah Penurunan Fungsi
1. Kaidah Konstan
“Turunan dari sebuah konstanta selalu nol (0)”
0


dx
dy
maka
a
Y
2. Kaidah Pangkat
1
. 

 b
b
bX
a
dx
dy
maka
aX
Y
Contoh :
2. Y = 5x³ maka dy/dx = 5.3x³ˉ¹
dy/dx = 15x²

13. Optimasi Ekonomi
3. Kaidah Penurunan Fungsi
3. Kaidah Penjumlahan dan Pengurangan
3a. Y = 2X3 + 5X2 – 6X – 8
dy/dx = 6X2 + 10X1 – 6X0 - 0
dY/dX = 6X2 + 10X - 6
3b. Y = 6X5 - X2 – 2X + 5
dy/dx = 30X4 - 2X1 –2X0 + 0
dY/dX = 30X4 -2X – 2
4. Kaidah Hasil Dua Fungsi/Perkalian
)
(
)
(
.
x
f
V
dan
x
f
U
UdV
VdU
dx
dy
maka
V
U
Y






14. Optimasi Ekonomi
3. Kaidah Penurunan Fungsi
4. Kaidah Hasil Dua Fungsi/Perkalian
)
(
)
(
.
x
f
V
dan
x
f
U
UdV
VdU
dx
dy
maka
V
U
Y





Contoh:
4.Y =(2x-6)⁵(3x+7)⁶
Misal:U=(2x-6)⁵ V=(3x+7)⁶
du=5(2x-6)⁴.2 dv=6(3x+7)⁵.3
du=10(2x-6)⁴ dv=18(3x+7)⁵
dy/dx =(3x+7)⁶.[10(2x-6)⁴ ] +(2x-6)⁵.[18(3x+7)⁵]
=2(3x+7)⁵.(2x-6)⁴[5(3x+7) +9(2x-6)]
= 2(3x+7)⁵.(2x-6)⁴.(33x- 19)
5. Kaidah Pembagian Dua Fungsi
2
.
V
UdV
dU
V
dx
dy
maka
V
U
Y



Contoh:
5.Y = 2x-5
4x+1
Misal: U=2X-5 V=4X+1
du=2 dv=4
dy/dx=(4x+1).2 – (2x-5).4
(4x+1)²
= 8x+2 – 8x – 20
(4x+1)²
= – 18
(4x+1)²

15. Optimasi Ekonomi
3. Kaidah Penurunan Fungsi
6. Fungsi dari Fungsi
)
(
.
. 1
x
f
U
dU
bU
a
dx
dy
maka
aU
Y b
b


 
Contoh :
6a. Y = 5 ( 3x – 6 ) ⁶ 6b. Y = 5(x²-3x+2)⁶
misal: u = 3x – 6 misal: u=x²-3x+2
du= 3 du=2x-3
dy/dx = 6.5(3x – 6)⁵.(3) dy/dx=30(x²-3x+2)⁵.(2x-3)
dy/dx = 90(3x – 6) ⁵ dy/dx= (60x-90)(x²-3x+2) ⁵
7. Kaidah Rantai
)
(
.
)
(
x
f
t
dx
dt
dt
dy
dx
dy
maka
t
f
Y



Contoh :
7. Y = t2 + t + 3 dimana t = 2x + 1
dy/dt = 2t + 1 ; dt/dx = 2
dy/dx = dy/dt.dt/dx
dy/dx = (2t + 1).2
= 4t + 2
= 4(2x + 1) + 2
dy/dx = 8x + 6

16. Optimasi Ekonomi
4. Memaksimalkan dan Meminimalkan Fungsi
►Analisis optimisasi dapat mudah dijelaskan
dengan mempelajari proses perusahaan
dalam menentukan tingkat output yang
memaksimumkan laba total.
►Jenis Optimisasi :
1. Optimisasi Maksimum
2. Optimisasi Minimum
Optimasi Maksimum (hal hal yang baik)
- Maksimum profit dengan kendala…..
- Maksimumkan manfaat dengan kendala
minimnya fasilitas
Optimasi Minimum (hal hal yang buruk)
- Minimum kerugian dengan kendala
tingginya biaya
- Minimum kegagalan produki dengan
minimnya sarana
- Minimum kecelakaan kerja dengan kendala
disiiplin kerja yang rendah

17. Optimasi Ekonomi
4. Memaksimalkan dan Meminimalkan Fungsi
𝒅²𝒚
𝒅²𝒙
= 𝐥𝐢𝐦
∆𝒙→𝟎
∆𝒀
∆𝑿
𝒅𝒚
𝒅𝒙
= 𝐥𝐢𝐦
∆𝒙→𝟎
∆𝒀
∆𝑿
Y = 2x⁴ – 5x3+3x2
Turunan I
Turunan II
Contoh Soal
𝒅𝒚
𝒅𝒙
= 8x3 –
15x2+6x
Turunan I
𝒅𝒚
𝒅𝒙
= 24x2 – 30x+6 Turunan II
𝒅(𝑻𝑹)
𝒅Q
=0

18. Contoh Soal
TR = 100Q – 10Q2
Aturan :
+ Berarti Minimasi
- Berarti Maksimasi
TR = 100Q – 10Q2
TR = 100 – 20Q
𝒅(𝑻𝑹)
𝒅Q
=0
TR = 100 – 20Q = 0
Q =
𝟏𝟎𝟎
𝟐𝟎
=5
Turunan II
TR = 100 – 20Q = 0
𝒅2 (𝑻𝑹)
𝒅Q2
TR = 100 – 20Q = 0
𝒅2(𝑻𝑹)
𝒅Q2 =-20
- Berarti Maksimasi
Turunan I
Optimasi Ekonomi
4. Memaksimalkan dan Meminimalkan Fungsi

19. Optimasi Ekonomi
4. Memaksimalkan dan Meminimalkan Fungsi
Optimasi Terkendala
Seorang Manajer Produksi ditugaskan
meminimumkan TC dalam
memproduksi sejumlah produk dari
perusahaan
Seorang Manajer Produksi ditugaskan
memaksimumkan output dari suatu
departement
Contoh Manajer Produksi
Contoh Marketing
Memaksimumkan penjualan per unit
produk dengan periode tertentu
Meminimumkan anggaran biaya
advertising
Masalah Maksimasi Masalah Minimasi
Maksimasi :
- Laba, Penerimaan, dan output
Bergantung pada :
- Kendala Sumber Daya
Minimasi :
- Biaya, Reject product, Kecelakaan
Bergantung pada :
- Kendala Kuantitas dan Kualitas
Output

20. Optimasi Ekonomi
4. Memaksimalkan dan Meminimalkan Fungsi
?. Kendala X + Y = 20
TC = 3(20 - Y)2 + 6Y2-(20-Y)Y
= 3(400 - 40Y + Y2) + 6Y2-(20Y-Y2)
= 1200 – 120Y + 3Y2+ 6Y2-20Y-Y2
= 1200 – 140Y + 10Y2
Tetapi menghadapi kendala bahwa output komoditas X ditambah output
komoditas Y harus sebesar 20.
Perusahaan ABC berusaha memaksimumkan fungsi laba total (TC), Sbb :
Dengan menyelesaikan kendala X dan mensubstitusikan nilai tsb ke dalam fungsi tujuan maka :
Contoh Soal :
: X = 20 - Y
TC = 3X2 + 6Y2-XY
Langkah I

21. Optimasi Ekonomi
4. Memaksimalkan dan Meminimalkan Fungsi
𝒅𝑻𝑪
𝒅𝒀
= -140+20Y = 0
20Y = 140
Y = 7
Langkah II
Langkah III
Turunan I Turunan II
𝒅2𝑻𝑪
𝒅𝒀2 = -140+20Y
𝒅2𝑻𝑪
𝒅𝒀2 = 20Y
𝑿 + 𝒀 = 𝟐𝟎
𝑿 + 𝟕 = 𝟐𝟎
𝑿 = 1𝟑
TC = 3X2 + 6Y2-XY
TC = 3(13)2 + 6(7)2-(13x7)
= 507 + 294 - 91
= 710
Langkah IV