Makalah ini membahas hukum-hukum termodinamika dan aplikasinya dalam kehidupan sehari-hari, menjelaskan perubahan energi, usaha, dan kalor dalam sistem termodinamik. Tujuan dari makalah ini adalah untuk memberikan pemahaman yang lebih baik tentang prinsip-prinsip dasar termodinamika, termasuk hukum pertama dan kedua, serta berbagai proses yang berlaku. Penulis juga mengharapkan umpan balik untuk memperbaiki makalah ini di masa mendatang.

1. Kata Pengantar
Puja dan puji syukur kami panjatkan kehadirat Tuhan Yang Maha Esa, karena berkat dan
rahmat-Nya, Makalah Fisika yang berjudul “TERMODINAMIKA” ini dapat diselesaikan.
Makalah ini bertujuan untuk memberikan informasi tentang hukum-hukum termodinamika
dan serba-serbinya, sehingga diharapkan nantinya pembaca dapat lebih memahami materi
termodinamika dalam fisika.
Tentunya karya tulis ini selesai berkat bantuan dari berbagai pihak yang telah memberikan
kontribusi yang sangat berarti bagi penyusunan laporan ini, baik berupa moril maupun materiil.
Untuk itu, kami ucapkan terima kasih yang mendalam kepada :
1. Semua pihak yang tidak dapat kami sebutkan satu persatu yang telah memberikan
bantuan yang cukup besar dalam penyusunan makalah ini.
Makalah ini sangat jauh dari sempurna dan masih banyak terdapat kesalahan-kesalahan
dalam penyusunan makalah ini, maka dari itu, kami mohon maaf yang sebesar-besarnya. Selain
itu, saran, usul dan kritik yang sifatnya membangun sangat kami harapkan demi penyempurnaan
di masa yang akan datang.
Akhir kata, semoga makalah ini dapat berguna dan bermanfaat bagi semua pihak.

2. Daftar Isi
1. Kata pengantar……………………………………………………………...1
2. Daftar isi……………………………………………………………………2
3. BAB I Pendahuluan……………………………………………………….3
1.1 Latar belakang………………………………………….3
1.2 Tujuan…………………………………………………..3
4. BAB II Pembahasan……………………………………………………….4
2.1 Pengertian Termodinamika…………………………….4
a. System Termodinamika……………………………4
b. Pengertian Energi dalam…………………………...5
c. Formulasi Usaha, Kalor dan Energi Dalam………..5
d. Gas ideal …………………………………………6
e. Kapasitas Panas……………………………………7
f. Entropi……………………………………............11
g. Pemuaian…………………………………………14
2.2 Proses Termodinamika………………………………15
a. Polytropic proses ………………………………..17
b. Proses isotermal ( suhu konstan ) ………………17
c. Isochoric proses ( volum konstan )………………20
d. Proses isobarik ( tekanan konstan )………………21
e. Proses adiabatik …………………………………24
f. Proses isentropik ………………………………...32
g. Isenthalpic proses …………………………….....34
h. Quasistatic proses ………………………………..35
2.3 Menentukan Usaha Luar Secara Grafik ……………..37
2.4 Hukum ke Nol Termodinamika………………………38
2.5 Hukum Pertama Termodinamika…………………….41
2.6 Hukum Kedua Termodinamika………………………44
2.7 Hukum Ketiga Termodinamika………………………47
2.8 Siklus Termodinamika………………………………53
2.9 Tabel Persamaan Termodinamika …………………..60
5. BAB III Penutup …………………………………………………………74
3.1 Kesimpulan …………………………………………74
3.2 Daftar Pustaka ………………………………………75
3.3 Latihan soal……………………………………..........76

3. BAB I
Pendahuluan
1.1 Latar Belakang
Setiap kali kita mengendarai kendaraan bermotor, menghidupkan AC atau
pendingin ruangan ataupun menggunakan peralatan elektronik lainnya, sebenarnya kita
telah memanfaatkan penerapan termodinamika. Di dalam termodinamika, nantinya kita
akan menemukan 3 hukum. Hukum ke nol termodinamika, kita mempelajari bagaimana
karakteristik-karakteristik berbagai benda ketika kita mengubah suhunya. Hukum
pertama termodinamika merupakan kelanjutan dari hukum kekekalan energi yang
diperluas hingga meliputi pertukaran energi, baik melalui perpindahan panas maupun
kerja mekanik serta memperkenalkan konsep energi dalam sebuah sistem. Hukum
pertama termodinamika yang akan kita pelajari ini memegang peranan yang sangat
penting dalam berbagai aspek kehidupan manusia sehari-hari.
Dalam kehidupan sehari-hari, banyak peristiwa yang berlangsung secara alami pada satu
arah tetapi tidak dapat berlangsung pada arah yang sebaliknya. Misalnya, panas selalu
mengalir dari suhu tinngi ke suhu rendah, tak pernah sebaliknya. Mengapa demikian?
Kita dapat mengubah seluruh energi mekanik menjadi panas dengan mudah, misalnya
pada saat kita menginjak rem untuk menghentikan kendaraan. Untuk arah sebaliknya,
yaitu mengubah panas menjadi energi mekanik, diperlukan peralatan yang cukup rumit.
Misalnya, kita dapat melihat contohnya pada mesin mobil. Bahkan, para ahli sekalipun
belum berhasil menciptakan mesin yang mampu mengubah seluruh panas menjadi energi
mekanik. Mengapa?
Jawaban kedua pertanyaan diatas berkaitan dengan arah proses dan merupakan salah satu
pokok pembahasan hukum kedua termodinamika. Hukum ini menjelaskan prinsip dasar
efisiensi mesin. Hukum ini juga mampu menjelaskan batas energi minimum yang
diperlukan untuk menjalankan mesin pendingin. Jadi, hukum kedua termodinamika
selalu berkaitan dengan persoalan praktis dalam kehidupan sehari-hari.
1.2 Tujuan
Adapun tujuan atau indikator dari materi ini adalah:
 Dapat menganalisis keadaan gas karena perubahan suhu, tekanan dan volume.
 Dapat menggambarkan perubahan keadaan gas dalam diagram p – V, V – T, dan p –
T.
 Dapat memformulasikan hukum I termodinamika dan penerapannya.
 Dapat memformulasikan hukum II termodinamika dan penerapannya.
 Dapat mengaplikasikan hukum I dan II termodinamika pada maslah fisika sehari-
hari.
 Dapat membedakan serta merumuskan proses reversible dan irreversible.

4. BAB II
Pembahasan
2.1 Pengertian Termodinamika
Ada beberapa pengertian dari Termodinamika:
1. Termodinamika adalah cabang ilmu fisika yang mempelajari pertukaran energi
dalam bentuk kalor dan kerja, sistem pembatas (boundary) serta lingkungan.
2. Termodinamika adalah ilmu yang mempelajari hubungan antara panas, kerja
mekanik serta aspek-aspek lain dari energi dan perpindahannya.
3. Termodinamika adalah suatu cabang ilmu fisika yang mempelajari hukum-hukum
dasar yang dipatuhi oleh kalor dan usaha.
Sistem Termodinamika
Dalam fisika, dikenal 3 macam sistem sebagai berikut:
1. Sistem Terbuka; ada pertukaran massa dan energi sistem dengan lingkungannya.
Contoh: lautan, tumbuh-tumbuhan.
2. Sistem Tertutup; ada pertukaran energi tetapi tidak terjadi pertukaran massa sistem
dengan lingkungannya. Contoh: Green house ada pertukaran kalor tetapi tidak terjadi
pertukaran kerja dengan lingkungan.
3. Sistem Terisolasi; tidak ada pertukaran massa dan energi sistem dengan lingkungan.
Contoh: tabung gas yang terisolasi.
Suatu sistem dapat berupa seperangkat mesin, refrigerant pada mesin pendingin,
uap air dalam turbin, jaringan otot makhluk hidup dan sebagainya. Jika pada sistem itu
dapat terjadi pertukaran energi dengan lingkungannya, misalnya melalui konduksi, maka
sistem itu disebut sebagai sistem termodinamika. Sebagai contoh, perhatikan sebuah
panci tertutup yang penuh berisi air. Ketika panci dipanaskan diatas kompor, energi
diberikan ke dalam air melalui peristiwa konduksi. Ketika air mendidih, air mampu
mengangkat tutup panci. Peristiwa ini dapat kita jumpai pada saat kita memanaskan air.
Dalam peristiwa ini keadaan air berubah, karena pada saat mendidih, volume, suhu dan
tekanan berubah. Proses semacam ini dikenal sebagai proses termodinamika. Dalam
sistem termodinamika, kita perlu mendefinisikan sistem dengan jelas. Misalnya, pada
proses pemanasan air diatas, yang dimaksud sistem adalah air, tetapi tidak termasuk
panci, tutup dan kompor.
Dalam proses termodinamika, kita perlu mengetahui besarnya panas Q yang
ditambahkan ke sistem dan kerja W yang ditambahkan oleh sistem. Besaran Q dan W ini
dapat bernilai positif, negative atau nol. Nilai Q posistif melambangkan aliran panas
yang masuk ke dalam system, sedangkan Q negative melambangkan aliran panas yang
keluar dari sistem. Nilai W positif melambangkan kerja yang dihasilkan oleh ekspansi
gas, dan berkaitan dengan energi yang meningglkan sistem. Nilai W negative, seperti
yang terjadi ketika gas mengalami kompresi, dimana kerja diberikan terhadap gas oleh
lingkungannya, melambangkan kerja yang dilakukan terhadap sistem. Kita akan
menggunakan perjanjian tanda ini secara konsisten.

5. Pengertian Energi Dalam
Sebelum membahas lebih lanjut mengenai hukum pertama termodinamika kita
harus memahami terlebih dahulu mengenai usaha, kalor dan energi serta energi dalam.
Karena sebelumnya kita telah membahas mengenai usaha, kalor dan energi, maka yang
perlu dibahas sekarang adalah mengenai energi dalam.
Setiap benda memiliki energi yang tidak tampak dari luar. Energi ini disebut
energi dalam. Energi dalam berhubungan dengan aspek mikroskopik zat. Kita ketahui
bahwa setiap zat terdiri atas atom-atom atau molekul molekul yang bergerak terus-
menerus. Dari gerakan ini, zat memiliki energy kinetik. Antara molekul-molekul zat juga
terdapat gaya yang disebut gaya antarmolekul. Karena gaya antarmolekul ini, molekul-
molekul memiliki energi potensial. Jumlah energi kinetik dan energi potensial yang
berhubungan dengan atom-atom atau molekul-molekul zat disebut energi dalam. Untuk
gas ideal, gaya antarmolekul dapat diabaikan, sehingga energi potensial molekul-
molekul adalah nol. Dengan demikian, energi dalam hanyalah total energi kinetik dari
seluruh molekul.
Energi dalam adalah suatu sifat mikroskopik zat, sehingga tidak dapat diukur
secara langsung. Yang dapat diukur secara tidak langsung adalah perubahan energi
dalam (notasi ΔU), yaitu ketika sistem berubah dari keadaan awal (diberi indeks 1) ke
keadaan akhir (diberi indeks 2).
Perubahan energi dalam : ΔU = U2 – U1
Formulasi Usaha, Kalor dan Energi Dalam
a. Formulasi Usaha
Proses yang terjadi pada tekanan tetap disebut proses isobarik. Usaha W dapat
dihitung dari persamaan: W=F.s dengan F adalah besar gaya dan s adalah besar
perpindahan. Gaya F ditimbulkan oleh tekanan gas ρ yang bekerja pada bagian bawah
pengisap, yang besarnya F=p.A, sehingga usaha W dapat ditulis: W=(p.A).s. Karena As
sama dengan perubahan volum gas, ΔV=V2-V1, dengan V2 dan V1 adalah volum akhir
dan awal. Maka usaha W dapat dinyatakan oleh persamaan:
Usaha pada proses isobarik: W = p.ΔV = p(V2-V1)
Rumus W = p.ΔV pada persamaan diatas hanya dapat digunakan untuk menghitung
usaha gas pada tekanan tetap (proses isobarik). Jika tekanan gas berubah, usaha W harus
dihitung dengan cara integral. Secara umum, usaha dihitung dengan persamaan integral
berikut:
Rumus umum usaha gas: W = ∫ p dV
Usaha diferensial dW yang dilakukan gas selama perpindahan :
dW = F.ds = ( pA )( ds ) = p ( A ds )
= p dV
b. Formulasi Kalor
Kalor yang diserap atau diberikan oleh sistem gas dapat dihitung dari rumus
kalor:
Q = m.c.Δt atau Q = C.Δt
Dengan c adalah kalor jenis dan C adalah kapasitas kalor gas.

6. c. Formulasi Energi Dalam
Telah kita ketahui bahwa untuk gas ideal, energy dalam gas sama dengan total
energy kinetik dari seluruh molekul-molekul gas. Formulasi energy dalam adalah
sebagai berikut:
Gas monoatomik: U = 3/2 NkT = 3/2 nRT
Gas diatomik: U = 5/2 NkT = 5/2 nRT
Dengan n = jumlah molekul
N = besar mol
K = tetapan Boltzman (k = 1,38 x 1023
J/K)
R = tetapan umum gas (R = 8,31 J/mol = 8310 J/kmol).
Tentu saja perubahan energy dalam ΔU untuk system yang berubah dari suhu awal T1 ke
suhu akhir T2 dapat dinyatakan sebagai berikut:
Gas monoatomik: ΔU = 3/2 nRΔT = 3/2 nR(T2-T1)
Gas diatomic: ΔU = 5/2 nRΔT = 5/2 nR(T2-T1)
Dengan ΔU = U2 – U1.
Persamaan diatas dengan jelas menunjukkan bahwa perubahan energi dalam sistem
hanya bergantung pada suhu awal dan suhu akhir. Dengan kata lain, perubahan energi dalam
ΔU hanya bergantung pada keadaan awal dan akhir sistem, dan tidak bergantung pada lintasan
yang ditempuh sistem untuk mencapai keadaan itu. Karena itu, energi dalam termasuk fungsi
keadaan.
Gas Ideal
Sebuah gas ideal adalah teori gas yang terdiri dari satu set bergerak-acak, non-
berinteraksi titik partikel . Konsep gas ideal berguna karena mematuhi hukum gas ideal, yang
disederhanakan, dan setuju untuk analisis dalam.
Pada kondisi normal seperti suhu dan tekanan standar, paling nyata gas berperilaku
kualitatif seperti gas ideal. Banyak gas seperti udara, nitrogen, oksigen, hidrogen, gas mulia, dan
beberapa gas yang lebih berat seperti karbon dioksida dapat diperlakukan seperti gas ideal dalam
toleransi yang wajar. Secara umum, gas berperilaku seperti gas ideal pada tinggi suhu dan
rendah density (yaitu lebih rendah tekanan), sebagai pekerjaan yang dilakukan oleh gaya
antarmolekul menjadi kurang signifikan dibandingkan dengan partikel ' energi kinetik, dan
ukuran molekul menjadi kurang signifikan dibandingkan dengan ruang kosong di antara mereka.
Model gas ideal cenderung gagal pada suhu rendah atau tekanan yang lebih tinggi, ketika
pasukan antarmolekul dan ukuran molekul menjadi penting. Hal ini juga gagal untuk gas berat
kebanyakan, seperti banyak refrigeran , dan untuk gas dengan pasukan antarmolekul yang kuat,
terutama uap air. Pada beberapa titik suhu rendah dan tekanan tinggi, gas nyata menjalani fase
transisi, seperti ke sebuah cairan atau padat. Model gas ideal, bagaimanapun, tidak
menggambarkan atau mengizinkan transisi fase. Ini harus dimodelkan dengan lebih kompleks
persamaan umum.
Model gas ideal telah dieksplorasi di kedua dinamika newton (seperti dalam " teori
kinetik") dan dalam mekanika kuantum (sebagai " gas dalam kotak"). Model gas ideal juga telah

7. digunakan untuk model perilaku elektron dalam logam (dalam model yang drude dan model
elektron bebas), dan itu adalah salah satu model yang paling penting dalam mekanika statik.
Jenis-jenis gas ideal
Ada tiga kelas dasar gas ideal:
 klasik atau Maxwell-Boltzmann gas ideal,
 kuantum yang ideal Bose gas , terdiri dari boson , dan
 kuantum yang ideal Fermi gas , terdiri dari fermion .
The gas ideal klasik dapat dipisahkan menjadi dua jenis: The gas ideal klasik
termodinamika dan gas kuantum yang ideal Boltzmann. Keduanya pada dasarnya sama, kecuali
bahwa gas termodinamika klasik yang ideal didasarkan pada klasik mekanika statistik , dan
parameter termodinamika tertentu seperti entropi hanya ditentukan ke dalam aditif belum
ditentukan konstan. Kuantum yang ideal Boltzmann gas mengatasi keterbatasan ini dengan
mengambil limit dari kuantum Bose gas dan kuantum gas Fermi dalam batas suhu tinggi untuk
menentukan konstanta ini aditif. Perilaku gas Boltzmann kuantum adalah sama seperti yang
dilakukan oleh gas ideal klasik kecuali untuk spesifikasi konstanta ini. Hasil dari gas Boltzmann
kuantum digunakan dalam sejumlah kasus termasuk persamaan Sackur-tetrode untuk entropi gas
ideal dan ionisasi persamaan Saha untuk lemah terionisasi plasma .
gas ideal klasik termodinamika
Sifat termodinamika The gas ideal dapat dijelaskan oleh dua persamaan: The persamaan
keadaan dari gas ideal klasik adalah hukum gas ideal
Persamaan ini berasal dari Hukum Boyle: (Pada T konstan dan n); Hukum Charles:
(Pada P konstan dan n), dan Hukum Avogadro: (Pada T konstan dan P).
Dengan menggabungkan tiga hukum, itu akan menunjukkan bahwa yang
berarti bahwa . Dalam kondisi ideal, atau lebih tepatnya
. The energi internal gas ideal diberikan oleh:
dimana

8.  P adalah tekanan
 V adalah volume yang
 n adalah jumlah zat gas (dalam mol)
 R adalah konstanta gas (8,314 J · K -1
mol -1)
 T adalah temperatur absolut
 k adalah konstanta yang digunakan dalam Hukum Boyle
 b adalah proporsionalitas konstan; sama dengan V / T
 adalah proporsionalitas konstan; sama dengan V / n
 U adalah energi internal
 adalah berdimensi spesifik kapasitas panas pada volume konstan, ≈ 3/2 untuk
gas monoatomik , 5/2 untuk diatomik gas dan 3 untuk molekul yang lebih
kompleks.
Jumlah gas di J · K -1
adalah
dimana
 N adalah jumlah partikel gas
 adalah konstanta Boltzmann (1.381 × 10 -23
J · K -1).
Distribusi probabilitas dari partikel dengan kecepatan atau energi yang diberikan oleh
distribusi Boltzmann .
Hukum gas ideal merupakan perpanjangan dari eksperimen menemukan hukum gas .
Nyata cairan di low density dan tinggi suhu mendekati perilaku gas ideal klasik. Namun, di
bawah suhu tinggi atau kepadatan , cairan nyata menyimpang kuat dari perilaku gas ideal,
terutama karena mengembun dari gas menjadi cair atau padat. Penyimpangan ini dinyatakan
sebagai faktor kompresibilitas .
Model gas ideal tergantung pada asumsi sebagai berikut:
 Molekul-molekul gas yang bisa dibedakan, kecil, bola keras
 Semua tumbukan elastis dan gerak semua gesekan (tanpa kehilangan energi
dalam gerakan atau tabrakan)
 Hukum Newton berlaku
 Jarak rata-rata antara molekul jauh lebih besar dari ukuran molekul
 Molekul-molekul selalu bergerak dalam arah acak dengan distribusi kecepatan
 Tidak ada kekuatan menarik atau tolak antara molekul atau lingkungan
Asumsi partikel berbentuk bola sangat diperlukan agar tidak ada mode rotasi
diperbolehkan, tidak seperti dalam gas diatomik. Berikut tiga asumsi yang sangat terkait:
molekul sulit, tabrakan yang elastis, dan tidak ada antar-molekul pasukan. Asumsi bahwa ruang
antara partikel jauh lebih besar daripada partikel itu sendiri adalah sangat penting, dan
menjelaskan mengapa pendekatan gas ideal gagal pada tekanan tinggi.

9. Kapasitas Panas
The kapasitas panas pada volume konstan nR = 1 J · K -1
gas apapun, termasuk gas ideal adalah:
Ini adalah kapasitas panas berdimensi pada volume konstan, yang umumnya merupakan fungsi
dari suhu karena gaya antarmolekul. Untuk suhu moderat, yang konstan untuk gas adalah
monoatomic sedangkan untuk gas diatomik adalah . Hal ini terlihat
bahwa pengukuran makroskopik pada kapasitas panas memberikan informasi tentang struktur
mikroskopis dari molekul.
Kapasitas panas pada tekanan konstan 1 · K -1
gas J ideal adalah:
dimana adalah entalpi gas.
Kadang-kadang, perbedaan dibuat antara gas ideal, di mana dan bisa bervariasi dengan
tekanan dan temperatur, dan gas yang sempurna , yang hal ini tidak terjadi.
Kapasitas kalor atau Harga air / Nilai air (H)
Kapasitas kalor suatu zat ialah banyaknya kalor yang diserap/dilepaskan untuk
menaikkan/menurunkan suhu 10
C
Jika kapasitas kalor/Nilai air = H maka untuk menaikkan/menurunkan suhu suatu zat
sebesar t diperlukan kalor sebesar :
Q dalam satuan k kal atau kal
H dalam satuan k kal / 0
C atau kal / 0
C
t dalam satuan 0
C
Kalor Jenis (c)
Kalor jenis suatu zat ialah : banyaknya kalor yang diterima/dilepas untuk
menaikkan/menurunkan suhu 1 satuan massa zat sebesar 10
C.
Jika kalor jenis suatu zat = c, maka untuk menaikkan/menurunkan suatu zat bermassa m,
sebesar t 0
C, kalor yang diperlukan/dilepaskan sebesar :
Q dalam satuan k kal atau kal
m dalam satuan kg atau g
c dalam satuan k kal/kg 0
C atau kal/g 0
C
t dalam satuan 0
C
Dari persamaan di atas dapat ditarik suatu hubungan :
Q = H . t
Q = m . c . t

10. H . t = m . c . t
Rambatan Kalor.
Panas dapat dipindahkan dengan 3 macam cara, antara lain :
a. Secara konduksi (Hantaran)
b. Secara konveksi (Aliran)
c. Secara Radiasi (Pancaran)
a. KONDUKSI.
Pada peristiwa konduksi, atom-atom zat yang memindahkan panas tidak berpindah tempat
tetapi hanya bergetar saja sehingga menumbuk atom-atom disebelahnya, (Misalkan terdapat
pada zat padat) Banyaknya panas per satuan waktu yang dihantarkan oleh sebuah batang
yang panjangnya L, luas penampang A dan perbedaan suhu antara ujung-ujungnya t,
adalah :
k adalah koefisien konduksi panas dari bahan dan
besarnya tergantung dari macam bahan.
Bila k makin besar, benda adalah konduktor panas yang
baik.
Bila k makin kecil, benda adalah isolator panas.
b. KONVEKSI.
Pada peristiwa ini partikel-partikel zat yang memindahkan panas ikut bergerak. Kalor yang
merambat per satuan waktu adalah :
h = koefisien konveksi
misalkan pada zat cair dan gas.
c. RADIASI.
Adalah pemindahan panas melalui radiasi energi gelombang elektromagnetik. Energi panas
tersebut dipancarkan dengan kecepatan yang sama dengan gelombang-gelombang
elektromagnetik lain di ruang hampa (3 x 108
m/det)
Banyaknya panas yang dipancarkan per satuan waktu menurut Stefan Boltzman adalah :
Besarnya harga e tergantung pada macam permukaan benda 0  e  1
- Permukaan hitam sempurna (black body)
- Sebagai pemancar panas ideal.
- Sebagai penyerap panas yang baik.
- Sebagai pemantul panas yang jelek.
- Terdapat pada permukaan yang lebih halus.
- Sebagai pemancar panas yang jelek.
- Sebagai penyerap panas yang jelek.
W = Intensitas radiasi yang dipancarkan per satuan luas,
dinyatakan dalam : J/m2
.det atau watt/m2
E = Emisivitas (Daya pancaran) permukaan
 = Konstanta umum = 5,672 x 10 –8
K)
(
m
watt
4
2

T = Suhu mutlak benda
H = m . c
H = k . A . L
t


H = h . A . t
W = e .  . T 4
e = 1
e = 0

11. - Sebagai pemantul yang baik.
Entropi
Entropi adalah properti dari sistem Thermodynamical. Sebuah sistem termodinamika
adalah setiap benda fisik atau wilayah ruang yang dapat dijelaskan oleh jumlah termodinamika
yang seperti temperatur , tekanan , Volume , dan kepadatan .
kita bisa mendefinisikan fungsi negara S, yang disebut entropi, yang memenuhi
Secara khusus, entropi adalah logaritma ukuran persamaan kepadatan :
di mana k B adalah konstanta Boltzmann , sama dengan 1.380 6 5 × 10 -23
JK -1.
Penjumlahan
adalah atas semua microstates kemungkinan sistem, dan P i adalah probabilitas bahwa sistem ini
dalam i th microstate. Untuk sebagian besar tujuan praktis, ini dapat diambil sebagai definisi
fundamental entropi karena semua formula lainnya untuk S dapat matematis berasal darinya,
namun tidak sebaliknya. (Dalam beberapa situasi langka dan terpendam, generalisasi dari
formula ini mungkin diperlukan untuk menjelaskan koherensi kuantum efek, tetapi dalam setiap
situasi di mana gagasan klasik probabilitas masuk akal, persamaan di atas secara akurat
menggambarkan entropi sistem.)
Dalam apa yang disebut asumsi dasar termodinamika statistik atau fundamental postulat dalam
mekanika statistik , pendudukan microstate pun diasumsikan sama kemungkinan (yaitu P i = 1 /
Ω Ω mana adalah jumlah microstates), asumsi ini . biasanya dibenarkan untuk sistem terisolasi
dalam kesetimbangan. Kemudian persamaan sebelumnya tereduksi menjadi:
perubahan Entropy
Ketika gas ideal mengalami perubahan, entropi yang juga bisa berubah. Untuk kasus-kasus di
mana panas spesifik tidak berubah dan baik volume, tekanan atau temperatur juga konstan,
perubahan entropi dapat dengan mudah dihitung.
Ketika panas spesifik dan volume yang konstan, perubahan entropi diberikan oleh:
.
Ketika panas spesifik dan tekanan yang konstan, perubahan entropi diberikan oleh:
.

12. Ketika panas spesifik dan suhu yang konstan, perubahan entropi diberikan oleh:
.
Dalam persamaan adalah panas spesifik pada volume konstan, adalah panas spesifik pada
tekanan konstan, adalah konstanta gas ideal , dan adalah jumlah mol gas.
Gas Ideal kuantum
Dalam persamaan Sackur-tetrode disebutkan di atas, pilihan terbaik dari konstanta
entropi ditemukan sebanding dengan kuantum panjang gelombang termal dari sebuah partikel,
dan titik di mana argumen logaritma menjadi nol kurang lebih sama dengan titik di mana jarak
rata-rata antara partikel menjadi sama dengan panjang gelombang termal. Bahkan, kuantum
teori itu sendiri memprediksi hal yang sama. Setiap gas berperilaku sebagai gas ideal pada suhu
cukup tinggi dan kepadatan cukup rendah, tetapi pada titik di mana persamaan Sackur-tetrode
mulai rusak, gas akan mulai berperilaku sebagai gas kuantum, terdiri dari baik boson atau
fermion . (Lihat gas dalam kotak artikel untuk derivasi dari gas kuantum yang ideal, termasuk
gas Boltzmann yang ideal.)
Gas cenderung berperilaku sebagai gas ideal pada rentang yang lebih luas dari tekanan
saat suhu mencapai suhu Boyle .
Gas Ideal Boltzmann
Gas Boltzmann yang ideal menghasilkan hasil yang sama seperti gas termodinamika
klasik, tetapi membuat identifikasi berikut untuk Φ konstan ditentukan:
mana Λ adalah de Broglie panjang gelombang termal gas dan g adalah degenerasi negara.
Gas Ideal Bose dan Fermi
Ideal gas boson (misalnya gas foton ) akan diatur oleh Bose-Einstein statistik dan
distribusi energi akan dalam bentuk distribusi Bose-Einstein . Ideal gas fermion akan diatur oleh
Fermi-Dirac statistik dan distribusi energi akan berada dalam bentuk distribusi Fermi-Dirac .
Pemuaian
Pemuaian adalah bertambahnya ukuran suatu benda karena pengaruh perubahan suhu
atau bertambahnya ukuran suatu benda karena menerima kalor.
Pemuaian panjang

13. Secara matematis persamaan yang digunakan untuk menentukan pertambahan panjang benda
setelah dipanaskan pada suhu tertentu adalah
Pemuaian luas
Untuk menentukan pertambahan luas dan volume akhir digunakan persamaan sebagai
berikut :
Pemuaian volume
Persamaan yang digunakan untuk menentukan pertambahan volume dan volume akhir suatu
benda tidak jauh beda pada perumusan sebelum. Hanya saja beda pada lambangnya saja.
Perumusannya adalah

14. 2.2 Proses Termodinamika
Sebuah proses termodinamika adalah pengembangan energik dari sistem
termodinamika melanjutkan dari keadaan awal ke keadaan akhir. Jalan melalui ruang variabel
termodinamika seringkali ditentukan dengan memegang variabel termodinamika tertentu
konstan. Sebuah fungsi negara adalah variabel termodinamika yang hanya bergantung pada
keadaan saat ini dari sistem, bukan jalan yang diambil untuk mencapai keadaan itu. Sebaliknya
suatu fungsi proses tidak bergantung pada jalan.
Ikhtisar
Contoh dari serangkaian proses termodinamika yang membentuk siklus Stirling
Sebuah proses termodinamika dapat divisualisasikan dengan grafis merencanakan
perubahan sistem variabel negara . Dalam contoh ini, empat proses yang akan ditampilkan.
Setiap proses memiliki awal yang terdefinisi dengan baik dan titik akhir dalam tekanan-volume
ruang keadaan . Dalam contoh khusus ini, proses 1 dan 3 adalah isotermal , sedangkan proses 2
dan 4 isochoric . The diagram PV adalah visualisasi sangat berguna dari sebuah proses, karena
area di bawah kurva dari sebuah proses adalah jumlah pekerjaan yang dilakukan oleh sistem
selama proses tersebut. Dengan demikian kerja dianggap sebagai variabel proses , seperti nilai
eksaknya tergantung pada jalan tertentu yang diambil antara titik awal dan akhir dari proses.
Demikian pula, panas dapat ditransfer selama proses, dan juga merupakan variabel proses.
Sebaliknya, tekanan dan volume (serta berbagai properti lainnya ) dianggap variabel negara
karena nilai-nilai mereka hanya bergantung pada posisi titik awal dan akhir, bukan jalur khusus
di antara mereka.
Tekanan - Volume
Para pasangan konjugasi tekanan-volume berkaitan dengan transfer energi mekanik atau
dinamis sebagai hasil dari pekerjaan.
 Sebuah proses isobarik terjadi pada tekanan konstan. Sebuah contoh akan memiliki
piston bergerak dalam silinder, sehingga tekanan dalam silinder selalu pada tekanan
atmosfer, meskipun terisolasi dari atmosfer. Dengan kata lain, sistem ini secara dinamis
terhubung, dengan batas bergerak, ke reservoir yang bertekanan konstan.

15.  Sebuah proses isochoric adalah satu di mana volume tetap konstan, yang berarti bahwa
pekerjaan yang dilakukan oleh sistem akan menjadi nol. Oleh karena itu, untuk sistem
yang sederhana dari dua dimensi, setiap energi panas ditransfer ke sistem eksternal akan
diserap sebagai energi internal. Sebuah proses isochoric juga dikenal sebagai proses
isometrik atau proses isovolumetric. Sebuah contoh akan menempatkan kaleng tertutup
dapat berisi udara hanya ke dalam api. Untuk pendekatan pertama, bisa tidak akan
berkembang, dan perubahan hanya akan bahwa gas keuntungan energi internal,
sebagaimana dibuktikan oleh peningkatan dalam suhu dan tekanan. Secara matematis,
. Kita bisa mengatakan bahwa sistem secara dinamis terisolasi, dengan
batas yang kaku, dari lingkungan.
Suhu - entropi
Para pasangan konjugasi temperatur-entropi berkaitan dengan transfer energi panas akibat
pemanasan.
 Sebuah proses isotermal terjadi pada suhu konstan. Sebuah contoh akan memiliki
sistem direndam dalam bak konstan suhu yang besar. Setiap pekerjaan yang dilakukan
oleh energi sistem akan hilang ke kamar mandi, tapi suhunya akan tetap konstan.
Dengan kata lain, sistem ini terhubung termal, dengan batas termal konduktif ke
reservoir suhu konstan.
 Sebuah proses adiabatik adalah proses di mana ada tidak ada energi ditambahkan atau
dikurangi dari sistem dengan pemanasan atau pendinginan. Untuk proses reversible, ini
identik dengan proses isentropik. Kita bisa mengatakan bahwa sistem termal terisolasi
dari lingkungannya dan bahwa batasnya adalah isolator termal. Jika sistem memiliki
entropi yang belum mencapai nilai kesetimbangan maksimum, entropi akan meningkat
meskipun sistem termal terisolasi. Dalam kondisi tertentu dua negara dari sistem dapat
dianggap adiabatik accesisble .
 Sebuah proses isentropik terjadi pada konstan entropi . Untuk proses reversibel ini
identik dengan proses adiabatik. Jika sistem memiliki entropi yang belum mencapai
keseimbangan maksimum nilai, proses pendinginan mungkin diperlukan untuk
mempertahankan bahwa nilai entropi.
 Polytropic proses
Sebuah proses polytropic adalah proses termodinamika yang mematuhi hubungan:
di mana P adalah tekanan, V adalah volume, n adalah setiap bilangan real ("index polytropic"),
dan C adalah konstanta. Persamaan ini dapat digunakan untuk secara akurat menggambarkan
proses tertentu sistem , terutama kompresi atau ekspansi dari gas , tetapi dalam beberapa kasus,
cairan dan padatan .
 Proses isotermal ( suhu konstan )

16. Sebuah proses isotermal adalah perubahan dari suatu sistem, di mana suhu tetap
konstan: Δ T = 0. Hal ini biasanya terjadi ketika sistem berada dalam kontak dengan reservoir
termal luar ( mandi panas ), dan perubahan terjadi perlahan-lahan cukup untuk memungkinkan
sistem untuk terus menyesuaikan diri dengan suhu reservoir melalui panas pertukaran.
Sebaliknya, suatu proses adiabatik adalah di mana sistem pertukaran panas dengan nya
lingkungan (Q = 0). Dengan kata lain, dalam proses isotermal, nilai Δ T = 0 tapi Q ≠ 0,
sedangkan dalam proses adiabatik, Δ T ≠ 0 tapi Q = 0.
Detail untuk gas ideal
Beberapa isoterm gas ideal pada diagram PV
Untuk kasus khusus dari gas yang hukum Boyle berlaku, produk pV adalah konstan jika gas
disimpan pada kondisi isotermal. Namun kasus-kasus di mana produk pv adalah istilah
eksponensial ini tidak sesuai. Nilai dari konstan nRT, dimana n adalah jumlah mol gas hadir dan
R adalah konstanta gas ideal . Dengan kata lain, hukum gas ideal pV = nRT berlaku. Ini berarti
bahwa
memegang. Keluarga kurva yang dihasilkan oleh persamaan ini ditunjukkan dalam grafik yang
disajikan di bagian bawah kanan halaman. Setiap kurva disebut isoterm. Grafik tersebut disebut
diagram indikator dan pertama kali digunakan oleh James Watt dan lain-lain untuk memantau
efisiensi mesin. Suhu yang sesuai untuk setiap kurva pada gambar meningkat dari kiri bawah ke
kanan atas.
Perhitungan pekerjaan

17. Daerah biru merupakan "pekerjaan" untuk perubahan isotermal
Dalam termodinamika, pekerjaan yang terlibat ketika perubahan gas dari negara A ke negara B
hanya
Untuk, isotermal reversibel proses, terpisahkan ini sama dengan daerah di bawah tekanan-
volume yang relevan isoterm, dan ditandai dengan warna biru pada gambar (di bagian bawah
kanan halaman) untuk gas ideal. Sekali lagi, p = nRT / V berlaku dan dengan T yang konstan
(karena ini adalah proses isotermal), kita memiliki:
Dengan konvensi, kerja didefinisikan sebagai sistem kerja yang tidak pada lingkungannya. Jika,
misalnya, sistem mengembang oleh piston bergerak ke arah gaya yang diterapkan oleh tekanan
internal gas, maka pekerjaan tersebut dihitung sebagai positif, dan sebagai pekerjaan ini
dilakukan dengan menggunakan energi internal sistem, hasilnya adalah bahwa energi internal
berkurang. Sebaliknya, jika lingkungan tidak bekerja pada sistem sehingga meningkatkan
internal energi, pekerjaan dihitung sebagai negatif.
Hal ini juga diperhatikan bahwa, untuk banyak sistem, jika suhu tetap konstan, energi internal
sistem juga konstan, dan sebagainya . Dari Hukum Pertama Termodinamika ,
, Sehingga dapat dikatakan bahwa untuk proses isotermal yang
sama.
Ketika tidak ada panas mengalir ke atau keluar dari gas karena suhu konstan, maka tidak ada
pekerjaan yang dilakukan. Dengan demikian, bekerja = 0 yang berarti tekanan eksternal adalah
nol. Ini disebut ekspansi bebas .
 Isochoric proses ( volum konstan )
Sebuah proses isochoric, juga disebut proses konstan-volume, proses isovolumetric,
atau proses isometrik, adalah proses termodinamika yang selama itu jumlah dari sistem tertutup

18. menjalani proses tersebut tetap konstan. Sebuah proses isochoric dicontohkan oleh pemanasan
atau pendinginan isi wadah, disegel inelastis: Proses termodinamika adalah penambahan atau
penghapusan panas, isolasi isi wadah menetapkan sistem tertutup, dan ketidakmampuan
kontainer untuk merusak memaksakan kondisi konstan-volume.
Formalisme
Sebuah proses termodinamika isochoric ditandai dengan konstan Volume , yaitu,
. Proses ini tidak ada tekanan -volume kerja , karena pekerjaan tersebut didefinisikan
oleh
,
di mana P adalah tekanan. Konvensi Tanda adalah sedemikian rupa sehingga kerja yang positif
dilakukan oleh sistem terhadap lingkungan.
Untuk proses reversibel , pada hukum pertama termodinamika memberikan perubahan dalam
sistem energi internal :
Mengganti bekerja dengan perubahan volume memberikan
Karena proses ini isochoric, , Persamaan sebelumnya sekarang memberikan
Menggunakan definisi kapasitas panas spesifik pada volume konstan,
,
Mengintegrasikan kedua belah pihak menghasilkan
Dimana adalah kapasitas panas spesifik pada volume konstan, adalah awal suhu dan adalah
final suhu . Kami menyimpulkan dengan:

19. Isochoric Proses dalam diagram Volume Tekanan . Pada diagram ini, meningkatkan tekanan,
tetapi volume tetap konstan.
Pada diagram Volume tekanan , proses isochoric muncul sebagai garis vertikal lurus. Konjugat
termodinamika, sebuah proses isobaric akan muncul sebagai suatu garis horisontal.
Etimologi
The isochor benda dan kata sifat isochoric berasal dari kata Yunani ἴσος (isos) yang
berarti "sama", dan χώρος (Choros) yang berarti "ruang."
 Proses isobarik ( tekanan konstan )
Sebuah proses isobarik adalah proses termodinamika dimana tekanan tetap konstan. Istilah ini
berasal dari bahasa Yunani isos, (sama), dan barus, (berat). Panas ditransfer ke sistem tidak
bekerja tetapi juga mengubah energi internal sistem:
Daerah kuning merupakan kerja yang dilakukan
Menurut hukum pertama termodinamika , di mana W adalah kerja yang dilakukan oleh sistem,
U adalah energi internal, dan Q adalah panas. Tekanan-volume pekerjaan oleh sistem tertutup
didefinisikan sebagai:

20. di mana Δ berarti perubahan atas seluruh proses, sedangkan d menunjukkan sebuah diferensial.
Karena tekanan konstan, ini berarti bahwa
.
pada proses isobarik P = C. maka besarnya usaha adalah
W = ∫ 𝑃. 𝑑𝑣
𝑉2
𝑉1
= P ( V2 – V1 ).
Menerapkan hukum gas ideal , ini menjadi
dengan asumsi bahwa jumlah gas tetap konstan, misalnya, tidak ada fase transisi selama reaksi
kimia . Menurut teorema equipartition , perubahan energi internal berkaitan dengan suhu sistem
dengan
,
dimana adalah panas spesifik pada volume konstan.
Mengganti dua persamaan terakhir ke persamaan pertama menghasilkan:
,
dimana adalah panas spesifik pada tekanan konstan.
kapasitas panas spesifik
Untuk menemukan kapasitas panas molar spesifik dari gas yang terlibat, persamaan berikut
berlaku untuk setiap gas umum yang calorically sempurna. Properti adalah baik disebut indeks
adiabatik atau rasio kapasitas panas . Beberapa sumber yang diterbitkan mungkin menggunakan
k bukan .
Molar panas spesifik isochoric:
.
Molar panas spesifik isobaric:
.

21. Nilai-nilai untuk adalah untuk gas diatomik seperti udara dan komponen utamanya ,
dan untuk gas monoatomik seperti gas mulia . Rumus untuk memanaskan spesifik akan
mengurangi dalam kasus khusus:
Monoatomik:
dan
Diatomik:
dan
Sebuah proses isobarik ditunjukkan pada diagram PV sebagai garis horizontal lurus,
menghubungkan negara termostatik awal dan akhir. Jika proses bergerak ke arah kanan, maka
itu adalah ekspansi. Jika proses bergerak ke arah kiri, maka itu adalah kompresi.
Mendefinisikan entalpi
Sebuah proses isochoric dijelaskan oleh persamaan . Ini akan mudah untuk
memiliki persamaan yang sama untuk proses isobarik. Mengganti persamaan kedua ke dalam
hasil pertama
Kuantitas U + p V adalah fungsi keadaan sehingga dapat diberikan nama. Hal ini disebut
entalpi , dan dilambangkan dengan H. Oleh karena itu proses isobarik dapat lebih ringkas
digambarkan sebagai
.
Entalpi dan kapasitas panas spesifik isobaric konstruksi matematika sangat berguna,
karena ketika menganalisis proses dalam sebuah sistem terbuka , situasi kerja nol terjadi ketika
cairan yang mengalir pada tekanan konstan. Dalam sebuah sistem terbuka, entalpi adalah jumlah
yang berguna untuk menggunakan untuk melacak kandungan energi dari fluida.
 Proses adiabatik
Sebuah proses adiabatik adalah setiap proses yang terjadi tanpa masukan atau output dari
panas dalam suatu sistem (yaitu selama proses sistem ini termodinamika terisolasi-tidak ada
perpindahan panas dengan lingkungan). Ini adalah kebalikan dari proses diabatic, di mana ada
perpindahan panas. Sebuah konsep kunci dalam termodinamika , banyak yang cepat proses
kimia dan fisika yang dijelaskan atau didekati dengan cara ini. Proses tersebut biasanya diikuti

22. atau didahului oleh peristiwa yang melakukan melibatkan panas transfer (yaitu non-adiabatik).
Contohnya termasuk transfer elektron .
Proses adiabatik dapat terjadi jika wadah sistem memiliki dinding termal-terisolasi atau
proses yang terjadi dalam waktu yang sangat singkat, sehingga tidak ada kesempatan untuk
pertukaran panas yang signifikan. Meskipun istilah adiabatik dan isokalori seringkali dapat
dipertukarkan, Proses adiabatik dapat dianggap sebagai bagian dari proses isokalori , subset
pelengkap sisa proses isokalori menjadi proses di mana perpindahan panas bersih tidak
menyimpang regional seperti dalam kasus ideal dengan media konduktivitas termal terbatas atau
tidak ada kapasitas termal.
Dalam proses ireversibel adiabatik, dQ = 0 tidak sama dengan TDS (TDS> 0) di mana Q
adalah energi panas, T adalah temperatur, dan S adalah entropi. dQ = TDS = 0 berlaku untuk
proses reversibel saja. Sebagai contoh, sebuah batas adiabatik adalah batas yang kedap
perpindahan panas dan sistem dikatakan adiabatik (atau termal) diisolasi, sebuah dinding
terisolasi mendekati suatu batas adiabatik. Contoh lain adalah temperatur nyala adiabatik , yang
merupakan suhu yang akan dicapai oleh api dengan tidak adanya kehilangan panas ke
lingkungan. Sebuah proses adiabatik yang reversibel juga disebut proses isentropik . Sebaliknya,
proses adiabatik yang ireversibel dan ekstrak pekerjaan tidak ada dalam isenthalpic proses,
seperti tarik kental, maju menuju perubahan non-negatif entropi.
Satu berlawanan ekstrim-yang memungkinkan perpindahan panas dengan lingkungan,
menyebabkan suhu tetap konstan-dikenal sebagai proses isotermal . Karena suhu termodinamika
konjugat ke entropi , proses isotermal adalah konjugasi untuk proses adiabatik untuk
transformasi reversibel.
Sebuah transformasi suatu sistem termodinamika dapat dianggap adiabatik ketika itu cukup
cepat bahwa tidak ada panas yang signifikan ditransfer antara sistem dan luar. Pada ekstrim
yang berlawanan, sebuah transformasi dari suatu sistem termodinamika dapat dianggap
isotermal jika cukup lambat sehingga suhu sistem tetap konstan dengan pertukaran panas
dengan luar.
Istilah "adiabatik" secara harfiah berarti dilewati, berasal dari akar Yunani ἀ-("tidak"), διὰ-
("melalui"), dan βαῖνειν ("lulus"); etimologi ini sesuai di sini untuk ketiadaan perpindahan panas
Adiabatik pemanasan dan pendinginan
Perubahan adiabatik suhu terjadi karena perubahan tekanan dari gas sementara tidak
menambah atau mengurangi setiap panas . Sebaliknya, ekspansi bebas adalah isotermal proses
untuk gas ideal.
Pemanasan adiabatik terjadi ketika tekanan gas yang meningkat dari pekerjaan yang
dilakukan di atasnya oleh lingkungannya, misalnya piston . Mesin diesel mengandalkan
pemanasan adiabatik saat langkah kompresi untuk meningkatkan suhu cukup untuk menyalakan
bahan bakar.

23. Pemanasan adiabatik juga terjadi di atmosfer bumi ketika massa udara turun, misalnya,
dalam angin katabatic atau Foehn atau chinook angin mengalir menurun selama pegunungan.
Ketika sebidang udara turun, tekanan pada peningkatan paket. Karena ini peningkatan tekanan,
volume paket ini menurun dan suhu yang meningkat, sehingga meningkatkan energi internal.
Pendinginan adiabatik terjadi ketika tekanan zat menurun karena tidak bekerja pada
sekitarnya. Pendinginan adiabatik terjadi di atmosfer bumi dengan mengangkat orografis dan
gelombang lee , dan ini dapat membentuk pileus atau awan lenticular jika udara didinginkan di
bawah titik embun . Ketika tekanan diterapkan pada sebidang menurun udara, udara dalam paket
diperbolehkan untuk memperluas, dengan meningkatnya volume, suhu turun dan energi internal
berkurang.
Pendinginan adiabatik tidak harus melibatkan cairan. Salah satu teknik yang digunakan
untuk mencapai suhu yang sangat rendah (seperseribu bahkan sepersejuta derajat di atas nol
mutlak) adalah demagnetisation adiabatik , di mana perubahan medan magnet pada bahan
magnetik yang digunakan untuk menyediakan pendinginan adiabatik. Juga, isi dari alam
semesta yang mengembang . (untuk urutan pertama) dapat digambarkan sebagai cairan
pendingin adiabatik (Lihat - kematian Panas alam semesta )
Magma naik juga mengalami pendinginan adiabatik sebelum letusan, sangat signifikan dalam
kasus magma yang naik dengan cepat dari kedalaman besar seperti kimberlites . [3]
Perubahan suhu tersebut dapat diukur dengan menggunakan hukum gas ideal , atau persamaan
hidrostatik untuk proses atmosfer.
Proses Tidak ada benar-benar adiabatik. Banyak proses yang dekat dengan adiabatik dan dapat
dengan mudah didekati dengan menggunakan asumsi adiabatik, tapi selalu ada beberapa
kehilangan panas, karena tidak ada isolator yang sempurna ada.
Ideal gas (proses reversible)

24. Untuk zat yang sederhana, selama proses adiabatik yang meningkat volume, energi internal dari
substansi kerja harus menurunkan
Persamaan matematika untuk gas ideal menjalani (yaitu, tidak ada generasi entropi) reversibel
proses adiabatik adalah
di mana P adalah tekanan, V adalah spesifik atau volume molar , dan
menjadi panas spesifik untuk tekanan konstan, menjadi panas khusus untuk volume
konstan, adalah indeks adiabatik , dan adalah jumlah derajat kebebasan (3 untuk gas
monoatomik, 5 untuk gas diatomik).
Untuk gas ideal monoatomik, , Dan untuk gas diatomik (seperti nitrogen dan oksigen ,
komponen utama dari udara ) . Perhatikan bahwa rumus di atas hanya berlaku untuk
gas ideal klasik dan tidak Bose-Einstein atau gas Fermi .
Untuk proses adiabatik reversibel, juga benar bahwa
di mana T adalah temperatur absolut.
Hal ini juga dapat ditulis sebagai
Penurunan rumus terus menerus untuk pemanasan dan pendinginan adiabatik
Definisi proses adiabatik adalah bahwa perpindahan panas ke sistem adalah nol, .
Kemudian, menurut hukum pertama termodinamika ,
dimana dU adalah perubahan energi internal sistem dan δW adalah kerja yang dilakukan oleh
sistem. Setiap pekerjaan (δW) dilakukan harus dilakukan dengan mengorbankan U energi
internal, karena tidak ada δQ panas sedang dipasok dari sekitarnya. Tekanan-volume pekerjaan
δW dilakukan oleh sistem didefinisikan sebagai

25. Namun, P tidak tetap konstan selama proses adiabatik melainkan berubah bersama dengan V.
Hal ini diinginkan untuk mengetahui bagaimana nilai-nilai dan dP dV berhubungan satu sama
lain sebagai hasil proses adiabatik. Untuk gas ideal energi internal diberikan oleh
dimana adalah jumlah derajat kebebasan dibagi dua, R adalah konstanta gas universal dan n
adalah jumlah mol dalam sistem (konstan).
Persamaan Membedakan (3) dan penggunaan hukum gas ideal , , Hasil
Persamaan (4) sering dinyatakan sebagai karena .
Sekarang persamaan pengganti (2) dan (4) ke dalam persamaan (1) untuk mendapatkan
menyederhanakan:
dan membagi kedua sisi dengan PV:
Setelah mengintegrasikan sisi kiri dan kanan dari V ke dan dari untuk p dan mengubah sisi
masing-masing,
Exponentiate kedua belah pihak,
dan menghilangkan tanda negatif untuk memperoleh
Oleh karena itu,

26. dan
Penurunan rumus diskrit
Perubahan energi internal dari suatu sistem, diukur dari negara ke negara 1 2, sama dengan
Pada saat yang sama, kerja yang dilakukan oleh tekanan-perubahan volume sebagai akibat dari
proses ini, sama dengan
Karena kita memerlukan proses untuk menjadi adiabatik, persamaan berikut harus benar
Dengan derivasi sebelumnya,
Mengatur ulang (4) memberikan
Mensubstitusikan ini ke (2) memberikan
Mengintegrasikan,
Mengganti ,

27. Mengatur ulang,
Menggunakan hukum gas ideal dan dengan asumsi jumlah molar konstan (seperti yang sering
terjadi dalam kasus-kasus praktis),
Dengan rumus terus menerus,
Atau,
Mensubstitusikan ke dalam ekspresi sebelumnya untuk ,
Mengganti ungkapan ini dan (1) dalam (3) memberikan
Menyederhanakan,
Menyederhanakan,

28. Menyederhanakan,
Dalam proses adiabatik tidak ada kalor yang masuk (diserap) ataupun keluar
(dilepaskan) oleh sistem (Q = 0). Dengan demikian, usaha yang dilakukan gas sama dengan
perubahan energi dalamnya (W = ∆U).
Jika suatu sistem berisi gas yang mula-mula mempunyai tekanan dan volume masing-
masing p1 dan V1 mengalami proses adiabatik sehingga tekanan dan volume gas berubah
menjadi p2 dan V2, usaha yang dilakukan gas dapat dinyatakan sebagai
Dimana γ adalah konstanta yang diperoleh perbandingan kapasitas kalor molar gas pada tekanan
dan volume konstan dan mempunyai nilai yang lebih besar dari 1 (γ > 1).
 Proses isentropik
Dalam termodinamika , proses proses atau isoentropic isentropik (ισον = "sama"
(Yunani), εντροπία entropi = "gangguan" (Yunani)) adalah satu di mana untuk tujuan analisis
teknik dan perhitungan, seseorang dapat berasumsi bahwa proses berlangsung dari inisiasi
sampai selesai tanpa peningkatan atau penurunan entropi sistem, yaitu, entropi sistem tetap
konstan. Hal ini dapat dibuktikan bahwa setiap reversibel proses adiabatik adalah proses
isentropik.
Penurunan hubungan isentropik
Untuk sistem tertutup, perubahan total energi dari sebuah sistem adalah jumlah dari pekerjaan
yang dilakukan dan panas yang ditambahkan,
Pekerjaan reversibel dilakukan pada sistem dengan mengubah volume,
dimana adalah tekanan dan adalah Volume . Perubahan entalpi ( )
Diberikan oleh,

29. Kemudian untuk proses yang bersifat reversibel dan adiabatik (yaitu tidak ada perpindahan
panas terjadi), , Dan sebagainya . Semua proses adiabatik
reversibel yang isentropik. Hal ini menyebabkan dua pengamatan penting,
, Dan
Selanjutnya, banyak dapat dihitung untuk proses isentropik dari gas ideal. Untuk setiap
transformasi gas ideal, itu selalu benar bahwa
, Dan .
Menggunakan hasil umum yang berasal di atas untuk dan , Kemudian
, Dan
.
Jadi untuk gas ideal, rasio kapasitas panas dapat ditulis sebagai,
Untuk gas ideal adalah konstan. Oleh karena itu pada mengintegrasikan persamaan di atas,
dengan asumsi gas yang sempurna, kita mendapatkan
yaitu
Menggunakan persamaan keadaan untuk gas ideal, ,
juga, untuk konstan (Per mol),
dan

30. Jadi untuk proses isentropik dengan gas ideal,
Tabel hubungan isentropik untuk gas ideal
Berasal dari:
Dimana:
 = Tekanan
 = Volume
 = Rasio spesifik memanaskan =
 = Suhu
 = Massa
 = Gas konstan untuk gas tertentu =
 = Konstanta gas Universal
 = Berat molekul gas tertentu
 = Density
 = Panas spesifik pada tekanan konstan

31.  = Panas spesifik pada volume konstan
 Proses Isenthalpic
Sebuah proses isenthalpic proses atau isoenthalpic adalah proses yang berlangsung tanpa
perubahan entalpi , H, atau entalpi spesifik , h.
Dalam proses tunak, steady-aliran, perubahan yang signifikan pada tekanan dan suhu dapat
terjadi pada cairan dan belum proses akan isenthalpic jika tidak ada transfer panas ke atau dari
lingkungan, tidak ada kerja yang dilakukan pada atau oleh lingkungan , dan tidak ada perubahan
energi kinetik dari cairan. (Jika proses tunak, steady-aliran dianalisis dengan menggunakan
kontrol volume segala sesuatu di luar kendali volume dianggap lingkungan. )
The Proses throttling adalah contoh yang baik dari proses isenthalpic. Pertimbangkan
pencabutan katup lega atau katup pengaman pada bejana tekan. Entalpi spesifik dari cairan di
dalam bejana tekan adalah sama dengan entalpi spesifik rumit karena lolos dari katup. [2]
Dengan pengetahuan tentang entalpi spesifik dari cairan, dan tekanan luar bejana tekan, itu
adalah mungkin untuk menentukan suhu dan kecepatan dari fluida melarikan diri.
Dalam proses isenthalpic:


Proses Isenthalpic pada gas ideal mengikuti isoterm sejak .
 Proses Quasistatic
Dalam termodinamika , proses quasistatic adalah proses termodinamika yang terjadi jauh
perlahan-lahan. Namun, sangat penting untuk dicatat bahwa tidak ada proses yang sebenarnya
adalah quasistatic. Oleh karena itu dalam prakteknya, proses tersebut hanya dapat didekati
dengan melakukan mereka amat sangat lambat.
quasistatic dan reversibilitas
Sebuah proses quasistatic memastikan bahwa sistem akan pergi melalui urutan negara
yang amat dekat dengan keseimbangan (sehingga sistem tetap dalam keseimbangan quasistatic
), dalam hal proses ini biasanya reversibel . Setiap proses reversibel adalah selalu satu
quasistatic. Namun, beberapa proses quasistatic yang ireversibel, jika ada panas yang mengalir
(dalam atau keluar dari sistem) atau jika entropi sedang dibuat dalam beberapa cara lain. Contoh
dari proses quasistatic yang tidak reversibel adalah kompresi terhadap sistem dengan piston
tunduk gesekan - Meskipun sistem selalu dalam kesetimbangan termal, gesekan memastikan
generasi entropi disipatif, yang secara langsung bertentangan dengan definisi reversibel. Sebuah
contoh penting dari sebuah proses yang bahkan tidak quasistatic adalah lambat pertukaran panas
antara dua mayat di dua temperatur finitely berbeda, di mana nilai tukar panas dikendalikan oleh
kurang adiabatik partisi antara dua badan (Sears dan Salinger, 1986) - di kasus ini, tidak peduli
seberapa lambat proses berlangsung, negara-negara dari dua mayat yang pernah amat dekat

32. dengan keseimbangan, karena kesetimbangan termal mensyaratkan bahwa dua mayat berada
tepat pada suhu yang sama.
Beberapa ambiguitas ada dalam literatur mengenai perbedaan antara proses quasistatic
dan reversibel, karena ini kadang-kadang diambil sebagai sinonim ( Bernard H Lavenda , 1978).
Alasannya justru karena teorema terbukti bahwa setiap proses reversibel juga merupakan salah
satu quasistatic, meskipun kami juga telah menunjukkan bahwa Kebalikannya tidak benar. Hal
ini praktis tidak berguna untuk membedakan antara kedua karena insinyur pun akan ingat untuk
memasukkan gesekan ketika menghitung generasi entropi disipatif. Definisi di atas lebih dekat
dengan pemahaman intuitif dari kata "quasi-" (hampir) "statis", namun tetap secara teknis
berbeda dari proses reversibel .
PV-Work di berbagai kuasi-statis proses
1. Konstan tekanan: proses isobaric ,
2. Konstan volume: proses isochoric ,
3. Suhu konstan: proses isotermal ,
Hubungan dengan proses yang ideal
Untuk nilai-nilai tertentu dari indeks polytropic, proses akan identik dengan proses umum
lainnya. Beberapa contoh dampak dari berbagai nilai indeks diberikan dalam tabel.
Variasi indeks polytropic
Polytropic
indeks
Hubungan Efek
-
Meskipun tidak berlaku untuk sistem sehari-hari, eksponen negatif
dapat berarti dalam beberapa kasus khusus yang tidak didominasi
oleh interaksi termal, seperti dalam proses plasma tertentu dalam
astro-fisika. [1]
(Konstan)
Setara dengan proses isobarik (konstan tekanan )

33. (Konstan)
Setara dengan proses isotermal (konstan suhu )
-
Sebuah proses kuasi-adiabatik seperti dalam mesin pembakaran
internal selama ekspansi, atau dalam refrigerasi kompresi uap
selama kompresi
- adalah indeks adiabatik , menghasilkan suatu proses
adiabatik (tidak ada panas yang ditransfer)
- Setara dengan proses isochoric (konstan Volume )
Ketika indeks n adalah antara dua nilai mantan (0, 1, gamma, atau tak terhingga), itu berarti
bahwa kurva polytropic [ klarifikasi diperlukan ]
akan dibatasi oleh kurva dari dua indeks yang sesuai.
Perhatikan bahwa , Karena .
Sebuah solusi untuk persamaan Lane-Emden menggunakan cairan polytropic dikenal sebagai
polytrope .
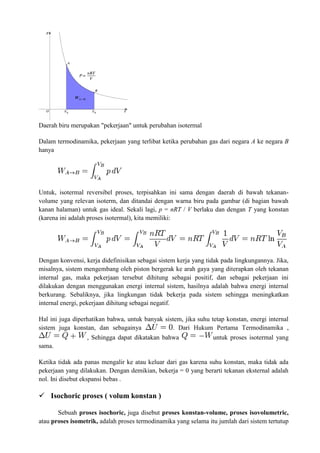
2.3 Menentukan Usaha Luar Secara Grafik
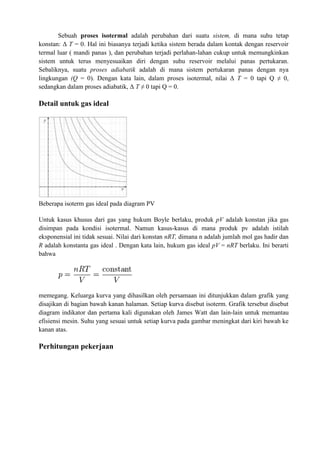
Usaha luar yang dilakukan oleh gas pada tekanan tidak tetap dapat dinyatakan dalam
diagram p – V, yang besarnya sebanding dengan luas daerah di bwah kurva.
 Proses kearah kanan
V2 > V1, berarti W positif
W = p ( V2 – V1 )
 Proses kearah kiri
V2 < V1, berarti W negative
W = -p ( V2 – V1 )
 Proses berbentuk siklus
Proses 1 ke 2 > W 0
Proses 2 ke 3 > W positif
Proses 3 ke 4 > W 0
Proses 4 ke 1 > W negative
Wtotal = ∆𝑝 . ∆𝑉
= ( p2 – p1 ) . ( V2 – V1 )
2.4 Hukum Ke Nol termodinamika
The zeroth hukum termodinamika adalah prinsip generalisasi dari kesetimbangan
termal antara badan-badan, atau sistem termodinamika , kontak.
Hukum zeroth menyatakan bahwa jika dua sistem berada dalam kesetimbangan termal
dengan sistem ketiga, mereka juga dalam kesetimbangan termal dengan satu sama lain.

34. Sistem dikatakan berada dalam kesetimbangan termal jika mereka mampu mentransfer
panas antara satu sama lain (misalnya dengan konduksi atau radiasi) tetapi tidak melakukannya.
Sistem juga dapat dikatakan berada dalam kesetimbangan termal jika mereka tidak dapat
mentransfer panas ke satu sama lain, tetapi tidak akan melakukannya jika mampu. Hukum
menyiratkan bahwa keseimbangan termal antara sistem adalah hubungan transitif , yang
memberikan definisi parameter fisik yang empiris, yang disebut temperatur . Suhu adalah sama
untuk semua sistem dalam kesetimbangan termal. Hukum memungkinkan pembangunan
termometer untuk mengukur properti ini.
Hukum zeroth sebagai hubungan kesetaraan
Suatu sistem dikatakan berada dalam kesetimbangan termal ketika tidak mengalami
perubahan bersih energi panas. Jika A, B, dan C yang berbeda sistem termodinamika , hukum
zeroth dari termodinamika dapat dinyatakan sebagai:
Jika A dan C masing-masing dalam kesetimbangan termal dengan B, A juga dalam
kesetimbangan dengan C.
Pernyataan ini menegaskan bahwa kesetimbangan termal adalah hubungan Euclidean antara
sistem termodinamika. Jika kita juga mengakui bahwa semua sistem termodinamika berada
dalam kesetimbangan termal dengan diri mereka sendiri, maka kesetimbangan termal juga
merupakan hubungan refleksif . Hubungan yang baik refleksif dan Euclidean adalah hubungan
kesetaraan . Salah satu konsekuensi dari penalaran ini adalah bahwa kesetimbangan termal
adalah hubungan transitif : Jika A berada dalam kesetimbangan termal dengan B dan B berada
dalam kesetimbangan termal dengan C, maka A berada dalam kesetimbangan termal dengan C.
Konsekuensi lain adalah bahwa hubungan kesetimbangan simetris : Jika A berada dalam
kesetimbangan termal dengan B, maka B berada dalam kesetimbangan termal dengan A. Dengan
demikian kita dapat mengatakan bahwa dua sistem berada dalam kesetimbangan termal dengan
satu sama lain, atau bahwa mereka berada dalam kesetimbangan bersama. Secara implisit
dengan asumsi kedua refleksivitas dan simetri, hukum zeroth Oleh karena itu sering dinyatakan
sebagai :
Jika dua sistem berada dalam kesetimbangan termal dengan sistem ketiga, maka mereka berada
dalam kesetimbangan termal dengan satu sama lain.
Sekali lagi, secara implisit dengan asumsi kedua refleksivitas dan simetri, hukum zeroth kadang-
kadang dinyatakan sebagai hubungan transitif: [4]
Jika A berada dalam kesetimbangan termal dengan B dan jika B berada dalam kesetimbangan
termal dengan C, maka A berada dalam kesetimbangan termal dengan C.
Thermal keseimbangan antara banyak sistem
Banyak sistem dikatakan dalam kesetimbangan jika, kecil pertukaran acak (karena gerak
Brown atau emisi foton , misalnya) di antara mereka tidak menyebabkan perubahan bersih pada
total energi dijumlahkan seluruh sistem. Contoh sederhana ini menggambarkan mengapa hukum
zeroth diperlukan untuk melengkapi deskripsi ekuilibrium.

35. Pertimbangkan sistem N di adiabatik terisolasi dari seluruh alam semesta, yaitu tidak ada
pertukaran panas di luar kemungkinan dari sistem N, yang semuanya memiliki volume konstan
dan komposisi, dan yang hanya dapat bertukar panas dengan satu sama lain.
Hukum Pertama dan Kedua gabungan berhubungan fluktuasi energi total, , Dengan suhu
sistem ke-i, dan entropi fluktuasi dalam sistem th i, sebagai berikut:
.
The adiabatic isolasi sistem dari alam semesta yang tersisa mensyaratkan bahwa jumlah total
dari fluktuasi entropi hilang, atau:
Artinya, entropi hanya dapat dipertukarkan antara sistem N. Kendala ini dapat digunakan untuk
mengatur ulang ekspresi untuk fluktuasi energi total dan mendapatkan:
dimana adalah suhu setiap j sistem kita dapat memilih untuk keluar tunggal antara sistem N.
Akhirnya, ekuilibrium memerlukan fluktuasi total energi menghilang, dalam hal:
yang dapat dianggap sebagai lenyapnya produk dari suatu matriks antisimetrik dan
vektor fluktuasi entropi . Agar solusi non-sepele untuk eksis,
Artinya, determinan dari matriks yang dibentuk oleh harus menghilang untuk semua
pilihan N. Namun, menurut teorema Jacobi , determinan dari N x N antisimetrik matriks selalu
nol jika N aneh, meskipun untuk N bahkan kami menemukan bahwa semua entri harus lenyap,
, Dalam rangka untuk mendapatkan penentu menghilang. Karenanya
pada kesetimbangan. Ini hasil non-intuitif berarti bahwa ganjil sistem selalu dalam ekuilibrium
terlepas dari suhu dan fluktuasi entropi, sementara kesetaraan suhu hanya diperlukan antara
jumlah bahkan sistem untuk mencapai keseimbangan dengan adanya fluktuasi entropi.
Hukum zeroth memecahkan paradoks ini aneh vs bahkan, karena dapat dengan mudah
digunakan untuk mengurangi sistem ganjil ke nomor bahkan dengan mempertimbangkan tiga
dari sistem N dan menghilangkan satu per penerapan prinsip, dan karenanya mengurangi

36. masalah bahkan untuk N yang kemudian mengarah ke kondisi ekuilibrium yang sama yang kita
harapkan dalam setiap kasus, yaitu, . Hasil yang sama berlaku untuk fluktuasi dalam
jumlah yang ekstensif, seperti volume (menghasilkan kondisi tekanan yang sama), atau fluktuasi
massa (yang mengarah ke kesetaraan kimia potensi). Oleh karena itu hukum zeroth memiliki
implikasi bagi banyak lebih dari suhu saja. Secara umum, kita melihat bahwa hukum zeroth
istirahat jenis tertentu asimetri hadir dalam Hukum Pertama dan Kedua.
Hukum zeroth menetapkan keseimbangan termal sebagai hubungan kesetaraan. Sebuah
hubungan kesetaraan pada set (seperti set sistem termal disetimbangkan) membagi set yang
menjadi koleksi himpunan bagian yang berbeda ("disjoint subset") di mana setiap anggota
himpunan adalah anggota dari satu dan hanya satu bagian tersebut. Dalam kasus hukum ke nol,
ini terdiri dari subset sistem yang berada dalam kesetimbangan bersama. Partisi ini
memungkinkan setiap anggota subset untuk menjadi unik "ditandai" dengan label
mengidentifikasi subset mana ia berasal. Meskipun label mungkin cukup sewenang-wenang, [5]
suhu adalah seperti proses pelabelan yang menggunakan sistem bilangan real untuk penandaan.
Hukum zeroth membenarkan penggunaan sistem termodinamika cocok sebagai termometer
untuk memberikan seperti pelabelan, yang menghasilkan sejumlah kemungkinan skala
temperatur empiris , dan membenarkan penggunaan hukum kedua termodinamika untuk
memberikan mutlak, atau suhu termodinamika skala. Skala temperatur tersebut membawa
kelangsungan tambahan dan memesan (misalnya, "panas" dan "dingin") properti dengan konsep
temperatur.
Dalam ruang parameter termodinamika, zona suhu konstan membentuk permukaan,
yang menyediakan tatanan alam dari permukaan di dekatnya. Satu Oleh karena itu dapat
membangun fungsi suhu global yang menyediakan pemesanan terus menerus negara. The
dimensi dari permukaan suhu konstan adalah salah satu kurang dari jumlah parameter
termodinamika, dengan demikian, untuk gas ideal digambarkan dengan tiga parameter
termodinamika P, V dan n, itu adalah dua- dimensi permukaan.
Misalnya, jika dua sistem gas yang ideal berada dalam kesetimbangan, maka P 1 V 1 / N 1 = P 2
V 2 / N 2 di mana P i adalah tekanan dalam sistem ke-i, V i adalah volume, dan N i adalah jumlah
(dalam mol , atau hanya jumlah atom) gas.
Permukaan PV / N = const mendefinisikan permukaan suhu termodinamika yang sama, dan satu
dapat label T mendefinisikan sehingga PV / N = RT, di mana R adalah beberapa konstan. Sistem
ini sekarang dapat digunakan sebagai termometer untuk mengkalibrasi sistem lain. Sistem
tersebut dikenal sebagai "termometer gas ideal".
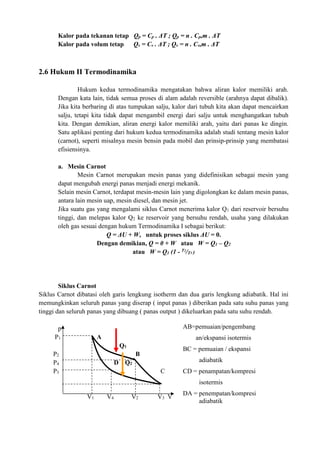
2.5 Hukum I Termodinamika
a. Pernyataan Hukum I Termodinamika
Hukum pertama termodinamika berhubungan dengan cara suatu sistem
memperoleh energi dalam dari lingkungan atau kehilangan energi dalam ke lingkungan.
Jika suatu sistem memperoleh energi Q dalam bentuk kalor dan pada saat yang sama
kehilangan energi W dalam bentuk usaha, perubahan energi dalam karena kedua faktor
ini dinyatakan oleh persamaan: ΔU = U2 – U1 = Q – W. Jadi, hukum pertama

37. termodinamika adalah prinsip kekekalan energi yang diaplikasikan pada kalor, usaha,
dan energi dalam.
Hukum pertama termodinamika:
Energi dalam suatu system berubah dari nilai awal U1 ke nilai akhir U2
sehubungan dengan kalor Q dan usaha W:
ΔU = U2 – U1 = Q – W
(perubahan energi dalam (ΔU) sistem = kalor (Q) yang ditambahkan ke sistem dikurangi
dengan kerja yang dilakukan oleh sistem)
Q adalah usaha positif jika sistem memperoleh kalor dan negatif jika kehilangan
kalor. Usaha W positif jika usaha dilakukan oleh sistem dan negatif jika usaha dilakukan
pada sistem.
Beberapa sumber lain menuliskan hukum pertama termodinamika sebagai berikut:
ΔQ = ΔU + ΔW
ΔQ = kalor yang masuk / keluar sistem
ΔU = perubahan energi dalam
ΔW = usaha luar.
b. Hukum I pada Berbagai Proses Termodinamika Gas
 Proses Isotermal
Pada proses isothermal, suhu awal gas T1 sama dengan suhu akhir gas T2 (atau
T2 = T1).
Dengan demikian, ΔU = 3
/2 nRT = 0. Hukum pertama termodinamika memberikan:
ΔU = Q – W; 0 = Q – W atau Q = W
Pada proses isothermal: ΔU = 0 dan Q = W
 Proses Isokhorik
Pada proses isokhorik, volum gas tetap (V1 = V2 atau ΔV = 0), sehingga usaha W
= 0.
Hukum pertama termodinamika memberikan:
ΔU = Q – W; ΔU = Q – 0 atau ΔU = Q
Pada proses isokhorik: W = 0 dan ΔU = Q
 Proses Adiabatik
Pada proses adiabatik, Q = 0, sehingga hukum pertama memberikan:
ΔU = Q – W; ΔU = 0 – W atau ΔU = -W
Pada proses adiabatik: Q = 0 dan ΔU = -W
Karena  Q = 0 maka O =  U +  W
U2 -U1 = -  W
Bila  W negatif ( -W = sistem ditekan ) usaha dalam sistem (  U ) bertambah. Sedangkan
hubungan antara suhu mutlak dan volume gas pada proses adibatik, dapat dinyatakan dengan
persamaan :
T.V-1 = konstan atau T1.V1-1 = T2.V2
-1
Usaha yang dilakukan pada proses adiabatik adalah :
W = m . cv ( T1 - T2 ) atau W =
P V
1 1
1
.

( V2
-1 - V1-1 )
Juga berlaku persamaan : P1.V1 = P2.V2


38.  Proses Isobarik
Pada proses isobarik: Q = ΔU + p.ΔV
Kapasitas Kalor Gas
a. Pengertian Kapasitas Kalor
Ada tiga besaran yang umum digunakan untuk menghitung kalor yang diterima
atau dilepaskan oleh suatu gas: kalor jenis, kapasitas kalor dan kapasitas kalor molar.
Ketiga besaran ini saling berhubungan, sehingga jika rumus salah satu rumus besaran
diketahui, maka rumus kedua besaran lainnya dapat diperoleh.
Kapasitas kalor suatu zat (C) adalah banyaknya kalor (Q) yang diperlukan untuk
menaikkan suhu suatu zat sebesar 1 kelvin.
C = Q/ΔT atau Q = C.ΔT
Satuan SI untuk kapasitas kalor adalah J/K atau J.K-1.
Kapasitas kalor gas pada tekanan tetap, Cp, didefinisikan sebagai kalor yang
diperlukan untuk menaikkan suhu suatu zat 1 kelvin pada tekanan tetap.
Kapasitas kalor pada tekanan tetap: Cp = Qp
/ΔT atau Qp = Cp.ΔT
Kapasitas kalor gas pada volum tetap, CV, didefinisikan sebagai kalor yang
diperlukan untuk menaikkan suhu suatu zat 1 kelvin pada volum tetap.
Kapasitas kalor pada volum tetap: CV = QV
/ΔT atau QV = CV.ΔT
Hubungan Cp dan Cv adalah sebagai berikut:
Cp – Cv = nR
Dengan n adalah banyak zat dalam mol dan R adalah tetapan umum gas.
b. Nilai Kapasitas Kalor dan Tetapan Laplace
Untuk gas monoatomik : Cv = 3/2 nR
Cp = 5/2 nR
Untuk gas diatomik : Cv = 5/2 nR
Cp = 7/2 nR
Tetapan Laplace (notasi γ) didefinisikan sebagai nilai perbandingan antara
kapasitas kalor pada tekanan tetap dengan kapasitas kalor pada volum tetap:
γ = Cp
/Cv
Perhatikan, Cp > Cv maka pastilah γ > 1.
Untuk gas monoatomik: Cp = 5
/2 nR dan Cv = 3
/2 nR, sehingga:
γ = 5/2 nR : 3/2 nR = 5/3 = 1,67
Untuk gas diatomik: Cp = 7
/2 nR dan Cv = 5
/2 nR, sehingga:
γ = 7/2 nR : 5/2 nR = 7/5 = 1,4
c. Kapasitas Kalor Molar
Selain besaran kapasitas kalor yang digunakan di fisika, dalam kimia lebih sering
digunakan besaran kapasitas kalor molar. Kapasitas kalor molar (notasi Cm) adalah
kapasitas kalor per mol.
Kapasitas kalor molar: Cm = C/n atau C = n.Cm
Dengan demikian dapat kita tulis:

39. Kalor pada tekanan tetap Qp = Cp . ΔT ; Qp = n . Cp,m . ΔT
Kalor pada volum tetap Qv = Cv . ΔT ; Qv = n . Cv,m . ΔT
2.6 Hukum II Termodinamika
Hukum kedua termodinamika mengatakan bahwa aliran kalor memiliki arah.
Dengan kata lain, tidak semua proses di alam adalah reversible (arahnya dapat dibalik).
Jika kita berbaring di atas tumpukan salju, kalor dari tubuh kita akan dapat mencairkan
salju, tetapi kita tidak dapat mengambil energi dari salju untuk menghangatkan tubuh
kita. Dengan demikian, aliran energi kalor memiliki arah, yaitu dari panas ke dingin.
Satu aplikasi penting dari hukum kedua termodinamika adalah studi tentang mesin kalor
(carnot), seperti misalnya mesin bensin pada mobil dan prinsip-prinsip yang membatasi
efisiensinya.
a. Mesin Carnot
Mesin Carnot merupakan mesin panas yang didefinisikan sebagai mesin yang
dapat mengubah energi panas menjadi energi mekanik.
Selain mesin Carnot, terdapat mesin-mesin lain yang digolongkan ke dalam mesin panas,
antara lain mesin uap, mesin diesel, dan mesin jet.
Jika suatu gas yang mengalami siklus Carnot menerima kalor Q1 dari reservoir bersuhu
tinggi, dan melepas kalor Q2 ke reservoir yang bersuhu rendah, usaha yang dilakukan
oleh gas sesuai dengan hukum Termodinamika I sebagai berikut:
Q = ΔU + W, untuk proses siklus ΔU = 0.
Dengan demikian, Q = 0 + W atau W = Q1 – Q2
atau W = Q1 (1 - T2
/T1 )
Siklus Carnot
Siklus Carnot dibatasi oleh garis lengkung isotherm dan dua garis lengkung adiabatik. Hal ini
memungkinkan seluruh panas yang diserap ( input panas ) diberikan pada satu suhu panas yang
tinggi dan seluruh panas yang dibuang ( panas output ) dikeluarkan pada satu suhu rendah.
p
P1 A
Q1
P2 B
P4 D Q2
P3 C
V1 V4 V2 V3 V
AB=pemuaian/pengembang
an/ekspansi isotermis
BC = pemuaian / ekspansi
adiabatik
CD = penampatan/kompresi
isotermis
DA = penempatan/kompresi
adiabatik

40. Siklus Carnot bekerja dengan mengubah kalor panas (heat) dan membuangnya dalam bentuk
kalor dingin (cold)
Mesin Pemanas
Mesin yang menggunakan siklus ini misalnya seperti mesin pemanas ruang dalam rumah seperti
di negara-negara sub tropis pada musim dingin.
Disini kalor panas (QH) sebagai Q1, dan kalor dingin (QC) sebagai Q2.
W = Q1 – Q2
Daya guna /efisiensi mesin kalor
1
Q
W

 x 100%
1
2
1
Q
Q
Q 

 x 100%
 =1
1
2
Q
Q
x 100% atau
 =1
1
2
T
T
x 100%
Untuk mesin Carnot ideal efisiensinya selalu maksimum.
Mesin Pendingin
Mesin pendingin seperti air conditioner (AC) maupun kulkas/refrigerator menggunakan proses
yang berbeda dengan proses mesin pemanas yang menggunakan siklus Carnot. Mesin
pendingin menyerap kalor dingin sebagai sumber dan membuangnya dalam bentuk kalor panas.
Gambar: Skema siklus Carnot

41. Gambar mesin kulkas Gambar mesin AC
Di sini kalor panas (QH) sebagai Q1, dan kalor dingin (QC) sebagai Q2.
Berlaku pula
W = Q1 – Q2
Efisiensi mesin pendingin sebagai berikut.
Daya guna /efisiensi mesin pendingin:
2
Q
W

 x 100%
2
2
1
Q
Q
Q 

 x 100%
 =
2
1
Q
Q
 1 x 100% atau
 =
2
1
T
T
 1 x 100%
Koefisien Performance mesin pendingin / koefisien daya guna sebagai berikut.
K =

1
K =
W
Q2
Gambar: Skema mesin pendingin

42. K =
2
1
2
Q
Q
Q

Hukum kedua termodinamika dapat dinyatakan dengan dua formulasi sebagai
berikut:
1. Formulasi Kelvin-Planck
Tidak mungkin untuk membuat sebuah mesin kalor yang bekerja dalam suatu
siklus yang semata-mata mengubah energy panas yang diperoleh dari suatu sumber pada
suhu tertentu seluruhnya menjadi usaha mekanik.
%
100
)
1
(
1
2



T
T

2. Formulasi Clausius
Tidak mungkin membuat mesin yang bekerja dalam satu siklus, mengambil
kalor dari suatu reservoir rendah dan memberikannya ke reservoir suhu tinggi tanpa
dilakukan usaha dari luar.
2.7 Hukum Ketiga termodinamika
Hukum ketiga termodinamika terkadang dinyatakan sebagai berikut:
The entropi dari sempurna kristal di nol mutlak adalah persis sama dengan nol.
Pada nol kelvin sistem harus dalam keadaan dengan kemungkinan minimal energi , dan
pernyataan dari hukum ketiga berlaku jika kristal yang sempurna hanya memiliki satu keadaan
energi minimum . Entropi berkaitan dengan jumlah microstates mungkin, dan dengan hanya satu
microstate tersedia di nol kelvin, entropi adalah persis nol.
Sebuah bentuk yang lebih umum dari hukum ketiga berlaku untuk sistem seperti kacamata yang
mungkin memiliki lebih dari satu keadaan energi minimum:
Entropi dari suatu sistem mendekati nilai konstan karena suhu mendekati nol.
Nilai konstan (tidak selalu nol) disebut entropi sisa dari sistem.
Secara fisik, hukum menyiratkan bahwa tidak mungkin untuk prosedur apapun untuk membawa
sistem ke nol mutlak suhu dalam jumlah terbatas langkah.
Pernyataan Hukum Ketiga Termodinamika :

43. • Suatu kristal sempurna pada temperatur nol mutlak mempunyai keteraturan sempurna →
entropinya adalah nol.
• Entropi suatu zat yang dibandingkan dengan entropinya dalam suatu bentuk kristal
sempurna pada nol mutlak, disebut Entropi Mutlak
• Makin tinggi temperatur zat, makin besar entropi mutlaknya
Penjelasan
Dalam istilah sederhana, menyatakan hukum ketiga bahwa entropi dari kristal sempurna
mendekati nol sebagai suhu mendekati nol mutlak. Undang-undang ini memberikan titik acuan
mutlak untuk penentuan entropi. Entropi ditentukan relatif terhadap titik ini adalah entropi
mutlak. Secara matematis, entropi mutlak sistem apapun pada suhu nol adalah log alami dari
jumlah B konstanta k tanah negara kali Boltzmann.
Entropi dari suatu kisi kristal yang sempurna seperti yang didefinisikan oleh teorema
Nernst ini adalah nol asalkan keadaan dasar adalah unik, karena ln (1) = 0.
Sebuah contoh dari sistem yang tidak memiliki keadaan dasar yang unik adalah salah
satu yang mengandung setengah-bulat berputar , yang waktu pembalikan simetri memberikan
dua merosot keadaan dasar. Untuk sistem tersebut, entropi pada suhu nol setidaknya ln (2) k B
(yang diabaikan pada skala makroskopis). Beberapa sistem kristal menunjukkan frustrasi
geometris , di mana struktur kisi kristal mencegah munculnya keadaan dasar yang unik. Ground-
state helium (kecuali di bawah tekanan) tetap cair.
Selain itu, gelas dan solusi yang solid mempertahankan entropi besar di 0K, karena
mereka adalah koleksi besar negara hampir merosot, di mana mereka menjadi terperangkap
keluar dari keseimbangan. Contoh lain yang solid dengan banyak hampir-degenerate keadaan
dasar, terperangkap keluar dari keseimbangan, adalah es Ih , yang memiliki "gangguan proton" .
Untuk entropi nol mutlak untuk menjadi nol, momen magnetik dari kristal sempurna
memerintahkan harus diri mereka sempurna memerintahkan, memang, dari perspektif entropis,
ini dapat dianggap sebagai bagian dari definisi "kristal sempurna". Hanya feromagnetik ,
antiferromagnetik , dan diamagnetik bahan dapat memenuhi kondisi ini. Bahan yang tetap
paramagnetik pada 0K, sebaliknya, mungkin memiliki keadaan dasar banyak hampir-merosot
(misalnya, dalam kaca spin ), atau dapat mempertahankan gangguan dinamis (a cairan berputar
).
formulasi Matematika
Pertimbangkan sebuah sistem tertutup dalam keseimbangan internal. Karena sistem berada
dalam kesetimbangan tidak ada proses ireversibel sehingga produksi entropi adalah nol. Selama
gradien suhu panas pasokan yang dihasilkan dalam materi, namun produksi entropi terkait dapat
disimpan cukup rendah jika panas diberikan perlahan-lahan. Kenaikan entropi karena δ panas
tambah Q kemudian diberikan oleh
(1)

44. Kenaikan suhu δ T karena δ panas Q ditentukan oleh kapasitas panas C (T, X) sesuai dengan
(2)
The X Parameter adalah notasi simbolis untuk semua parameter (seperti tekanan, medan magnet,
cair / padat fraksi, dll) yang dijaga konstan selama pasokan panas. Misalnya jika volume
konstan kita mendapatkan kapasitas panas pada volume konstan C V. Dalam kasus fase transisi
dari cair ke padat, atau dari gas ke cair X parameter dapat menjadi sebagian kecil dari salah satu
dari dua komponen. Menggabungkan hubungan (1) dan (2) memberikan
(3)
Integrasi persamaan. (3) dari suhu acuan T 0 ke suhu T sewenang-wenang memberikan entropi
pada suhu T
(4)
Kita sekarang sampai pada formulasi matematis dari hukum ketiga. Ada tiga langkah:
1:. Dalam batas T 0 0 → integral di Persamaan (4) adalah terbatas. Sehingga kita dapat
mengambil T 0 = 0 dan menulis
(5)
2. nilai S (0, X) adalah independen dari X. Dalam bentuk matematika
(6)
Jadi persamaan. (5) dapat lebih disederhanakan
(7)
Persamaan (6) juga dapat dirumuskan sebagai
(8)
Dengan kata: pada nol mutlak semua proses isotermal yang isentropik. Persamaan. (8) adalah
formulasi matematis dari hukum ketiga.

45. 3: sebagai salah satu bebas untuk memilih nol entropi akan lebih mudah untuk mengambil
(9)
sehingga persamaan. (7) tereduksi menjadi bentuk akhir
(10)
Makna fisik Persamaan. (9) adalah lebih dari sekedar pilihan yang nyaman dari nol entropi. Hal
ini karena urutan yang sempurna nol kelvin seperti yang dijelaskan sebelumnya.
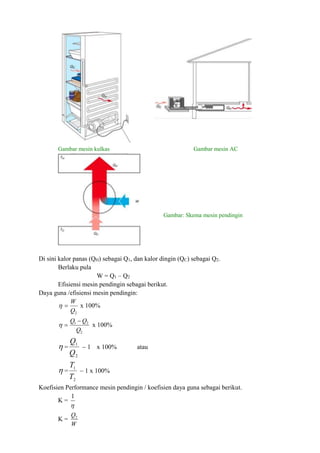
Konsekuensi dari hukum ketiga
Gambar 1 Sisi Kiri: Absolute nol dapat dicapai dalam jumlah terbatas langkah-langkah jika S (0,
X 1) ≠ S (0, X 2). Kanan: Sebuah jumlah tak terbatas langkah ini diperlukan karena S (0, X 1) = S
(0, X 2).
Hukum ketiga adalah setara dengan pernyataan bahwa
"Tidak mungkin dengan prosedur apapun, tidak peduli seberapa ideal, untuk mengurangi
suhu sistem apapun ke nol suhu dalam jumlah terbatas operasi terbatas".
Alasan bahwa T = 0 tidak dapat dicapai sesuai dengan hukum ketiga dijelaskan sebagai berikut:
Misalkan suhu suatu zat dapat dikurangi dalam proses isentropik dengan mengubah parameter X
dari X 2 X 1. Salah satu bisa memikirkan multistage demagnitization nuklir setup dimana medan
magnet dihidupkan dan dimatikan dengan cara yang terkontrol. [8]
Jika akan ada perbedaan
entropi pada nol mutlak T = 0 dapat dicapai dalam jumlah terbatas langkah. Namun, pada T = 0
tidak ada perbedaan entropi sehingga jumlah tak terbatas langkah akan diperlukan. Proses ini
diilustrasikan dalam Gambar 1.
panas spesifik

46. Misalkan bahwa kapasitas panas dari sampel di wilayah LT dapat didekati dengan C (T, X) = C 0
T α,
maka
(11)
Integral terbatas untuk T 0 → 0 jika α> 0. Jadi kapasitas panas dari semua zat harus pergi ke nol
pada nol mutlak
(12)
Panas spesifik molar pada volume konstan dari gas ideal monoatomik klasik, seperti helium
pada suhu kamar, diberikan oleh C V = (3/2) R dengan R molar gas ideal konstan. Pergantian
dalam Pers. (4) memberikan
(13)
Dalam batas T 0 0 → ini menyimpang ekspresi. Jelas kapasitas panas konstan tidak memenuhi
persamaan. (12). Ini berarti bahwa gas dengan kapasitas panas yang konstan sepanjang jalan ke
nol mutlak melanggar hukum ketiga termodinamika.
Konflik diselesaikan sebagai berikut: Pada suhu tertentu sifat quantum dari materi mulai
mendominasi perilaku. Partikel Fermi mengikuti Fermi-Dirac statistik Bose dan partikel
mengikuti statistik Bose-Einstein . Dalam kedua kasus kapasitas panas pada suhu rendah tidak
lagi suhu independen, bahkan untuk gas ideal. Untuk gas Fermi
(14)
dengan temperatur Fermi T F diberikan oleh
(15)
Berikut N adalah bilangan Avogadro, V m volume molar, dan M massa molar.
Untuk gas Bose
(16)
dengan T B diberikan oleh

47. (17)
Spesifik memanaskan diberikan oleh Persamaan (14) dan. (16) keduanya memenuhi persamaan.
(12).
Tekanan uap
Cairan hanya dekat nol mutlak adalah ³ Dia dan ⁴ Dia. Panas mereka penguapan memiliki nilai
membatasi diberikan oleh
(18)
dengan L 0 dan C konstanta p. Jika kita menganggap wadah, sebagian diisi dengan cairan dan
sebagian gas, entropi dari campuran cairan-gas
(19)
di mana S l (T) adalah entropi cairan dan x adalah fraksi gas. Jelas perubahan entropi selama
masa transisi cair-gas (x dari 0 ke 1) divergen dalam batas T → 0. Ini melanggar Persamaan. (8).
Alam memecahkan paradoks ini sebagai berikut: pada suhu di bawah sekitar 50 mK tekanan uap
yang sangat rendah sehingga kepadatan gas lebih rendah dari vakum terbaik di alam semesta.
Dengan kata lain: di bawah 50 mK ada cukup gas di atas cairan.
Laten panas mencair
Kurva pencairan dari ³ Dia dan ⁴ Dia baik memperpanjang turun ke nol mutlak pada tekanan
terbatas. Pada tekanan mencair cair dan padat berada dalam kesetimbangan. Hukum yang ketiga
menuntut bahwa entropi dari padat dan cair yang sama pada T = 0. Akibatnya panas laten
pencairan adalah nol dan kemiringan kurva leleh mengekstrapolasikan untuk nol sebagai hasil
dari persamaan Clausius-Clapeyron .
koefisien ekspansi termal
Koefisien ekspansi termal didefinisikan sebagai
(20)
Dengan hubungan Maxwell
(21)

48. dan persamaan (8) dengan X = p. terlihat bahwa
(22)
Jadi koefisien ekspansi termal dari semua bahan harus pergi ke nol nol kelvin.
2.8 Siklus Termodinamika
Sebuah siklus termodinamika terdiri dari serangkaian proses termodinamika
mentransfer panas dan kerja, sementara memvariasikan tekanan, temperatur, dan variabel negara
lainnya, akhirnya mengembalikan sistem ke keadaan awal. Dalam proses melalui siklus ini,
sistem dapat melakukan bekerja pada sekitarnya, sehingga bertindak sebagai mesin panas .
Jumlah negara tergantung hanya pada keadaan termodinamika , dan variasi kumulatif
sifat tersebut menambahkan hingga nol selama siklus. Proses kuantitas (jumlah atau path),
seperti panas dan kerja adalah proses tergantung, dan panas kumulatif dan pekerjaan non-nol.
The hukum pertama termodinamika menyatakan bahwa masukan panas yang bersih adalah sama
dengan output kerja bersih atas setiap siklus. Sifat mengulangi dari jalur proses memungkinkan
untuk terus beroperasi, membuat siklus konsep penting dalam termodinamika . Siklus
termodinamika sering menggunakan proses quasistatic untuk model kerja dari perangkat yang
sebenarnya.
Panas dan bekerja
Dua kelas utama siklus termodinamika adalah kekuatan siklus dan siklus pompa
panas. Siklus Power siklus yang mengubah beberapa masukan panas menjadi kerja mekanik
output, sedangkan siklus panas pompa mentransfer panas dari rendah ke suhu tinggi
menggunakan masukan kerja mekanik. Siklus seluruhnya terdiri dari proses quasistatic dapat
beroperasi sebagai kekuatan atau siklus pompa panas dengan mengendalikan arah proses. Pada
diagram Volume tekanan atau diagram temperatur entropi , yang searah jarum jam dan
berlawanan arah menunjukkan kekuasaan dan siklus pompa panas, masing-masing.
Hubungan dengan bekerja
Contoh diagram PV dari siklus termodinamika.

49. Karena variasi bersih properti negara selama siklus termodinamika adalah nol, membentuk loop
tertutup pada diagram PV. Sebuah diagram PV sumbu Y menunjukkan tekanan (P) dan sumbu X
menunjukkan volume (V). Daerah tertutup oleh loop adalah kerja (W) yang dilakukan oleh
proses:
Pekerjaan ini sama dengan keseimbangan panas (Q) ditransfer ke dalam sistem:
Persamaan (2) membuat proses siklus mirip dengan proses isotermal : meskipun perubahan
energi internal selama proses siklik, ketika proses siklik selesai energi sistem adalah sama
dengan energi itu ketika proses dimulai.
Jika proses siklus bergerak searah jarum jam di sekitar loop, maka W akan positif, dan itu
merupakan mesin panas . Jika bergerak berlawanan, maka W akan negatif, dan itu merupakan
pompa panas .
Kekuatan siklus
Diagram Panas mesin.
Siklus kekuasaan Termodinamika merupakan dasar untuk pengoperasian mesin panas,
yang memasok sebagian besar dunia tenaga listrik dan menjalankan sebagian besar kendaraan
bermotor . Siklus daya dapat dibagi sesuai dengan tipe mesin panas mereka berusaha untuk
model. Yang paling umum bahwa model siklus mesin pembakaran internal adalah siklus Otto ,
yang model mesin bensin dan siklus Diesel , yang model mesin diesel . Siklus bahwa model
mesin pembakaran eksternal meliputi siklus Brayton , yang model turbin gas , dan siklus
Rankine , yang model turbin uap .

50. Siklus termodinamika searah jarum jam ditunjukkan oleh panah menunjukkan bahwa
siklus merupakan mesin panas. Siklus ini terdiri dari empat negara (titik ditunjukkan oleh salib)
dan proses termodinamika empat (baris).
Misalnya tekanan-volume kerja mekanik dilakukan dalam siklus mesin panas, terdiri
dari 4 proses termodinamika, adalah:
Jika tidak ada perubahan volume yang terjadi dalam proses 4 -> 1 dan 2 -> 3, persamaan (3)
disederhanakan menjadi:
siklus pompa panas
Siklus panas Termodinamika pompa adalah model untuk pompa panas dan lemari es .
Perbedaan antara keduanya adalah bahwa pompa panas dimaksudkan untuk menjaga tempat
yang hangat saat lemari es dirancang untuk mendinginkannya. Siklus refrigerasi yang paling
umum adalah siklus kompresi uap , yang model sistem yang menggunakan refrigeran yang fase
perubahan. The siklus refrigerasi absorpsi merupakan alternatif yang menyerap refrigeran dalam
larutan cair daripada menguap itu. Gas siklus refrigerasi termasuk siklus Brayton terbalik dan
siklus Hampson-Linde . Regenerasi dalam pendingin gas memungkinkan untuk pencairan gas .
Pemodelan sistem nyata

51. Contoh sistem nyata dimodelkan dengan proses ideal: PV dan TS diagram siklus Brayton
dipetakan ke proses aktual dari mesin turbin gas
Siklus termodinamika dapat digunakan untuk model perangkat nyata dan sistem,
biasanya dengan membuat serangkaian asumsi. asumsi penyederhanaan sering diperlukan untuk
mengurangi masalah ke bentuk yang lebih mudah dikelola. Sebagai contoh, seperti yang
ditunjukkan pada gambar, perangkat seperti turbin gas atau mesin jet dapat dimodelkan sebagai
siklus Brayton . Perangkat yang sebenarnya terdiri dari serangkaian tahap, masing-masing itu
sendiri dimodelkan sebagai proses termodinamika ideal. Meskipun setiap tahap yang bekerja
pada fluida kerja adalah perangkat nyata yang kompleks, mereka dapat dimodelkan sebagai
proses ideal yang mendekati perilaku nyata mereka. Asumsi selanjutnya adalah bahwa gas
buang akan diteruskan kembali melalui inlet dengan kerugian yang sesuai panas, sehingga
menyelesaikan siklus ideal.
Perbedaan antara siklus ideal dan performa sebenarnya dapat menjadi signifikan. [2]
Sebagai
contoh, gambar berikut menggambarkan perbedaan dalam output kerja diprediksi oleh ideal
siklus Stirling dan kinerja aktual dari mesin Stirling:
Ideal Stirling siklus Realisasi kinerja
Aktual dan ideal dilapis,
menunjukkan perbedaan
dalam output kerja

52. Sebagai hasil kerja diwakili oleh interior siklus, ada perbedaan yang signifikan antara output
kerja prediksi siklus ideal dan output kerja yang sebenarnya ditunjukkan oleh mesin nyata. Hal
ini juga dapat diamati bahwa proses individu nyata menyimpang dari rekan-rekan ideal mereka,
misalnya, ekspansi isochoric (proses 1-2) terjadi dengan beberapa perubahan volume aktual.
siklus termodinamika terkenal
Dalam prakteknya, sederhana siklus termodinamika ideal biasanya terbuat dari empat proses
termodinamika . Setiap proses termodinamika dapat digunakan. Namun, ketika siklus ideal
dimodelkan, seringkali proses di mana satu variabel negara dipertahankan konstan digunakan,
seperti proses isotermal (suhu konstan), proses isobaric (tekanan konstan), proses isochoric
(volume konstan), proses isentropik (entropi konstan) , atau proses isenthalpic (entalpi konstan).
Seringkali proses adiabatik juga digunakan, di mana tidak ada panas yang dipertukarkan.
Beberapa siklus termodinamika contoh dan proses konstituen mereka adalah sebagai berikut:
Sepeda
Proses 1-2
(Compression)
Proses 2-3
(Penambahan
Panas)
Proses 3-4
(Ekspansi)
Proses 4-1
(Penolakan
Panas)
Catatan
Daya siklus normal dengan pembakaran eksternal - atau siklus pompa panas:
Bell
Coleman
adiabatik isobarik adiabatik isobarik
Sebuah Brayton siklus
terbalik
Carnot isentropik isotermal isentropik isotermal
Ericsson isotermal isobarik isotermal isobarik
kedua Ericsson siklus dari
1853
Rankine adiabatik isobarik adiabatik isobarik Mesin uap
Scuderi adiabatik
variabel
tekanan
dan volume
adiabatik isochoric
Stirling isotermal isochoric isotermal isochoric
Stoddard adiabatik isobarik adiabatik isobarik
Daya siklus normal dengan pembakaran internal :
Brayton adiabatik isobarik adiabatik isobarik
Mesin jet
versi pembakaran
eksternal siklus ini
dikenal sebagai pertama
siklus Ericsson dari 1.833
Disel adiabatik isobarik adiabatik isochoric
Lenoir isobarik isochoric adiabatik
Pulse jet
(Catatan: Proses 1-2
menyelesaikan keduanya
penolakan panas dan
kompresi)

53. Minyak
mawar
adiabatik isochoric adiabatik isochoric Bensin / mesin
Siklus Ideal
Sebuah ilustrasi dari sebuah mesin panas siklus yang ideal (panah searah jarum jam).
Sebuah siklus yang ideal dibangun dari:
1. TOP dan BOTTOM dari loop: sepasang proses isobaric paralel
2. KIRI dan KANAN dari loop: sepasang proses paralel isochoric
Carnot siklus
The Siklus Carnot adalah siklus terdiri dari benar-benar proses reversibel dari isentropik
kompresi dan ekspansi dan isotermal Selain panas dan penolakan. The Efisiensi termal dari
siklus Carnot hanya bergantung pada suhu mutlak dari dua waduk di mana perpindahan panas
berlangsung, dan untuk siklus daya:
dimana adalah suhu terendah siklus dan tertinggi. Untuk siklus Carnot listrik dengan
koefisien kinerja untuk pompa panas adalah:
dan untuk kulkas koefisien kinerja adalah:
Hukum kedua termodinamika membatasi efisiensi dan COP untuk semua perangkat siklik ke
tingkat pada atau di bawah efisiensi Carnot. The Siklus Stirling dan siklus Ericsson adalah dua

54. siklus reversibel lainnya yang menggunakan regenerasi untuk mendapatkan perpindahan panas
isotermal.
Stirling siklus
Siklus Stirling adalah seperti siklus Otto, kecuali bahwa adiabats diganti dengan isoterm.
Hal ini juga sama dengan siklus Ericsson dengan proses isobaric diganti untuk proses volume
konstan.
1. TOP dan BOTTOM dari loop: sepasang kuasi-paralel proses isotermal
2. KIRI dan KANAN sisi loop: sepasang proses paralel isochoric
Panas mengalir ke loop melalui isoterm atas dan isochore kiri, dan beberapa dari panas ini
mengalir kembali keluar melalui isoterm bawah dan isochore yang tepat, tetapi sebagian besar
aliran panas adalah melalui sepasang isoterm. Hal ini masuk akal karena semua pekerjaan yang
dilakukan oleh siklus dilakukan oleh sepasang proses isotermal, yang dijelaskan oleh Q = W.
Hal ini menunjukkan bahwa semua panas bersih masuk melalui isoterm atas. Bahkan, semua
panas yang datang melalui isochore kiri keluar melalui isochore yang tepat: karena isoterm atas
adalah semua pada suhu yang lebih hangat yang sama dan isoterm bawah adalah semua pada
temperatur dingin yang sama , Dan karena perubahan dalam energi untuk isochore suatu
sebanding dengan perubahan suhu, maka semua panas yang masuk melalui isochore kiri
dibatalkan tahu persis oleh panas akan keluar isochore yang tepat.
2.9 Tabel persamaan termodinamika
jumlah pokok Umum
Kuantitas (Nama umum / s)
(Umum) Simbol /
s
SI Unit Dimensi
Jumlah molekul N berdimensi berdimensi
Jumlah mol n mol [N]
Suhu T K [Θ]
Panas Energi Q, q J [M] [L] 2
[T] -2
Laten Panas Q L J [M] [L] 2
[T] -2
jumlah berasal Umum
Kuantitas (Nama
umum / s)
(Umum)
Simbol / s
Mendefinisikan Persamaan SI Unit Dimensi
Termodinamika
beta suhu, Inverse
β J -1 [T] 2
[M] -1
[L] -2
Entropi S JK -1 [M] [L] 2
[T] -2
[Θ] -1
Negentropy J JK -1 [M] [L] 2
[T] -2
[Θ] -1

55. Energi internal U J
[M] [L] 2
[T] -2
Entalpi H J
[M] [L] 2
[T] -2
Partisi Fungsi Z berdimensi berdimensi
Energi bebas Gibbs G J
[M] [L] 2
[T] -2
Kimia potensial
(dari
komponen i dalam
campuran)
μ i
(N i, S, V semua harus
konstan)
J
[M] [L] 2
[T] -2
Energi bebas
Helmholtz
Sebuah F, J
[M] [L] 2
[T] -2
Landau potensial ,
Landau Gratis
Energy
Ω J
[M] [L] 2
[T] -2
Potensi besar Φ G J
[M] [L] 2
[T] -2
Massieu Potensi,
Helmholtz gratis
entropi
Φ JK -1 [M] [L] 2
[T] -2
[Θ] -1
Planck potensial,
Gibbs bebas entropi
Ξ JK -1 [M] [L] 2
[T] -2
[Θ] -1
Thermal sifat materi
Kuantitas
(nama
umum / s)
(Umum
) simbol
/ s
Mendefinisikan persamaan SI unit Dimensi
Umum
panas /
kapasitas
termal
C JK -1
[M] [L] 2
[T] -2
[Θ] -
1
Kapasitas
panas
(isobarik)
C p JK -1
[M] [L] 2
[T] -2
[Θ] -
1
Kapasitas
panas
spesifik
(isobarik)
C mp J kg -1
K -1 [L] 2
[T] -2
[Θ] -1
Molar
kapasitas
panas
C np
JK -1
mol -
1
[M] [L] 2
[T] -2
[Θ] -
1
[N] -1

56. spesifik
(isobarik)
Kapasitas
panas
(isochoric /
volumetrik
)
C V JK -1
[M] [L] 2
[T] -2
[Θ] -
1
Kapasitas
panas
spesifik
(isochoric)
C mV J kg -1
K -1 [L] 2
[T] -2
[Θ] -1
Molar
kapasitas
panas
spesifik
(isochoric)
C nV
JK -1
mol -
1
[M] [L] 2
[T] -2
[Θ] -
1
[N] -1
Spesifik
panas laten
L J kg -1
[L] 2
[T] -2
Rasio
isobarik
terhadap
kapasitas
panas
isochoric,
panas rasio
kapasitas
indeks,
adiabatik
γ
berdimens
i
berdimens
i
Thermal transfer
Kuantitas (nama umum /
s)
(Umum)
simbol / s
Mendefinisikan
persamaan
SI unit Dimensi
Suhu gradien
Tidak ada
simbol
standar
K m -1
[Θ] [L] -1
Konduksi termal tingkat,
termal saat ini, termal /
panas fluks , transfer
daya termal
P
W = J s
-1
[M] [L] 2
[T] -2
Thermal intensitas Saya W m -2
[M] [T] -3
Termal / panas kerapatan
fluks (vektor analog
intensitas termal di atas)
q W m -2
[M] [T] -3

57. Persamaan
Fase transisi
Fisik Situasi Persamaan
Adiabatik transisi
Isotermal transisi Untuk gas ideal
Isobarik transisi
p 1 = p 2, p = konstanta
Isochoric transisi
V 1 = V 2, V = konstan
Adiabatik ekspansi
Gratis ekspansi
Pekerjaan dilakukan oleh gas
memperluas
Proses
Kerja Bersih Selesai dalam Proses Cyclic
Teori Kinetic
Ideal gas persamaan
Fisik Situasi Tata nama Persamaan
Ideal gas
hukum
 p = tekanan
 V = volume
kontainer
 T = temperatur
 n = jumlah mol
 N = jumlah
molekul
 k = konstanta
Boltzmann

58. Tekanan gas
ideal
 m = massa satu
molekul
 M m = massa molar
gas Ideal
Kuan
titas
Persamaan Umum
Isobarik
Δ p = 0
Isochoric
Δ V = 0
Isoterm
al
Δ T = 0
Adiabatik
Beker
ja
W
Panas
Kapa
sitas
C
(Seperti untuk gas
nyata)
(Untuk
gas ideal
monoato
mik)
(Untuk
gas ideal
monoato
mik)
Energ
i
intern
al
Δ U
Ental
pi
Δ H
Entro
pi
Δ S
[1]
Konst
an
Entropi
 , Di mana k B adalah konstanta Boltzmann , dan Ω menunjukkan volume
macrostate di ruang fase atau probabilitas termodinamika dinyatakan disebut.
 , Untuk proses reversibel hanya

59. Statistik fisika
Di bawah ini adalah hasil yang bermanfaat dari distribusi Maxwell-Boltzmann untuk gas ideal,
dan implikasi dari jumlah Entropy. Distribusi ini berlaku untuk atom atau molekul merupakan
gas yang ideal.
Fisik Situasi Tata nama Persamaan
Maxwell-
Boltzmann
distribusi
 v = kecepatan
atom / molekul,
 m = massa
setiap molekul
(semua
molekul adalah
identik dalam
teori kinetik),
 γ (p) = Faktor
Lorentz sebagai
fungsi dari
momentum
(lihat di bawah)
 Rasio termal
untuk
beristirahat
massa-energi
setiap molekul:
K 2 adalah Modifikasi
fungsi Bessel jenis
kedua.
Non-relativistik kecepatan
Relativistik kecepatan (Maxwell-Juttner
distribusi)
Entropi
Logaritma
dari
kepadatan
negara
 P i =
probabilitas
sistem di
microstate i
 Ω = jumlah
microstates
di mana:
Entropi
perubahan
Entropik
kekuatan

60. Equipartition
teorema
 d f = derajat
kebebasan
Rata-rata energi kinetik per derajat kebebasan
Energi internal
Kololari dari distribusi non-relativistik Maxwell-Boltzmann di bawah.
Fisik Situasi Tata nama Persamaan
Berarti kecepatan
Root mean
kecepatan persegi
Modal kecepatan
Berarti jalan
bebas
 σ = penampang Efektif
 n = Volume kepadatan
jumlah partikel sasaran
 ℓ = jalan bebas Rata-Rata
proses Kuasi-statis dan reversibel
Untuk kuasi-statis dan reversibel proses, hukum pertama termodinamika adalah:
di mana δ Q adalah panas yang dipasok ke sistem dan δ W adalah kerja yang dilakukan oleh
sistem.
potensi Termodinamika
Energi berikut ini disebut potensi termodinamika ,
Nama Simbol Rumus Natural variabel
Energi internal
Energi bebas Helmholtz
Entalpi
Energi bebas Gibbs
Landau Potensi (potensial Grand) ,

61. dan terkait hubungan termodinamika mendasar atau "persamaan master" [2]
adalah:
Potensi Diferensial
Energi internal
Entalpi
Energi bebas Helmholtz
Energi bebas Gibbs
hubungan Maxwell
Empat yang paling umum hubungan Maxwell adalah:
Fisik Situasi Tata nama Persamaan
Termodinamika
potensi sebagai
fungsi dari variabel
alami mereka
 =
internal energi
 =
Entalpi
 =
energi bebas
Helmholtz
 =
energi bebas
Gibbs
Hubungan mencakup berikut ini.
Persamaan diferensial lainnya adalah:
Nama H U G

62. Gibbs-
Helmhol
tz
persama
an
Quantum properti

 Dibedakan Partikel
di mana N adalah jumlah partikel, h adalah konstanta Planck , I adalah momen inersia , dan Z
adalah fungsi partisi , dalam berbagai bentuk:
Derajat kebebasan Partisi Fungsi
Terjemahan
Getaran
Rotasi  di mana:
 σ = 1 ( molekul heteronuklir )
 σ = 2 ( homonuclear )
Thermal sifat materi
Koefisien Persamaan
Joule-
Thomson
koefisien
Kompresibilit
as (suhu
konstan)

63. Koefisien
ekspansi
termal
(tekanan
konstan)
Kapasitas
panas
(tekanan
konstan)
Kapasitas
panas
(volume
konstan)
Derivasi dari kapasitas panas (tekanan konstan)
Sejak
Derivasi dari kapasitas panas (volume konstan)
Sejak
(Di mana δ W rev adalah kerja yang dilakukan oleh sistem),

64. Thermal transfer
Fisik Situasi Tata nama Persamaan
Net intensitas emisi
/ penyerapan
 T = temperatur eksternal
eksternal (di luar sistem)
 T = sistem internal yang
suhu (dalam sistem)
 ε = emmisivity
Energi internal dari
suatu zat
 C V = isovolumetric
kapasitas panas dari
substansi
 Δ T = perubahan suhu
zat
Meyer persamaan
 C p = kapasitas panas
isobarik
 C V = isovolumetric
kapasitas panas
 n = jumlah mol
Efektif termal
konduktivitas
 λ i = konduktivitas
termal zat i
 λ bersih konduktivitas
termal = setara
Seri
Paralel
efisiensi termal
Fisik Situasi Tata nama Persamaan
Termodinamika
mesin
 η = efisiensi
 W = kerja yang
dilakukan oleh mesin
 Q H = energi panas
pada reservoir suhu
tinggi
 Q C = energi panas
pada reservoir suhu
yang lebih rendah
 T H = suhu suhu yang
Termodinamika Mesin:
Carnot mesin efisiensi:

65. lebih tinggi. waduk
 T C = suhu suhu yang
lebih rendah. waduk
Pendinginan
 K = koefisien kinerja
pendinginan
Pendinginan kinerja
Carnot pendingin kinerja
 v
 t
 e
Cabang fisika
Inti
Divisi
 Eksperimental fisika
 Teoritis fisika
Energi
dan
gerak
 Klasik mekanika
o Newtonian
mekanik
o Lagrangian
mekanika
o Hamiltonian
mekanik
 Continuum mekanik
 Celestial mekanika
 Mekanika statistika
 Termodinamika
 Mekanika zat cair dan
gas
 Biomekanika
 Mekanika kuantum
Gelomba
ng dan
bidang
 Gravitasi
 Elektromagnetisme
 Quantum teori medan
 Kenisbian
o Relativitas khusus
o Relativitas umum
Terap
an
Fisik
ilmu dan
matemati
ka
 Akustik
 Fisika perbintangan
 Atom, molekul, dan
optik fisika

66.  Atom fisika
 Kimia fisika
 Komputasi fisika
 Publikasi materi fisika
 Tinggi fisika energi
 Matematika fisika
 Optik
 Fisika plasma
Biologi ,
geologi ,
ekonomi
 Biofisika
o Medis fisika
o Neurophysics
 Agrophysics
o Tanah fisika
 Atmosfer fisika
 Econophysics
 Geofisika
Diperoleh dari "
http://en.wikipedia.org/w/index.php?title=Table_of_thermodynamic_equations&oldid=5172912
59 "
BAB III
Penutup
3.1 Kesimpulan
Terdapat empat Hukum Dasar yang berlaku di dalam sistem termodinamika, yaitu:
 Hukum Awal (Zeroth Law) Termodinamika
Hukum ini menyatakan bahwa dua sistem dalam keadaan setimbang dengan sistem ketiga, maka
ketiganya dalam saling setimbang satu dengan lainnya.
 Hukum Pertama Termodinamika
Hukum ini terkait dengan kekekalan energi. Hukum ini menyatakan perubahan energi dalam
dari suatu sistem termodinamika tertutup sama dengan total dari jumlah energi kalor yang
disuplai ke dalam sistem dan kerja yang dilakukan terhadap sistem.
 Hukum kedua Termodinamika

67. Hukum kedua termodinamika terkait dengan entropi. Hukum ini menyatakan bahwa total
entropi dari suatu sistem termodinamika terisolasi cenderung untuk meningkat seiring dengan
meningkatnya waktu, mendekati nilai maksimumnya.
 Hukum ketiga Termodinamika
Hukum ketiga termodinamika terkait dengan temperatur nol absolut. Hukum ini menyatakan
bahwa pada saat suatu sistem mencapai temperatur nol absolut, semua proses akan berhenti dan
entropi sistem akan mendekati nilai minimum. Hukum ini juga menyatakan bahwa entropi
benda berstruktur kristal sempurna pada temperatur nol absolut bernilai nol.
3.2 Daftar Pustaka
HALLIDAY, RESNICK, WALKER. “ DASAR – DASAR FISIKA “
http://hyperphysics.phy-astr.gsu.edu/hbase/thermo/firlaw.html
http://thermodynamicslaw.blogspot.com/2011/12/about-thermodynamics-2.html
http://bowlesphysics.com/images/AP_Physics_B_-_Thermodynamics.ppt
http://en.wikipedia.org/wiki/Thermodynamic_process
http://www.transtutors.com/physics-homework-help/thermal-physics/thermodynamic-
process.aspx
http://www.britannica.com/EBchecked/topic/591572/thermodynamics/258543/Isothermal-and-
adiabatic-processes
http://translate.googleusercontent.com/translate_c?depth=1&hl=id&langpair=en|id&rurl=transla
te.google.co.id&u=http://en.wikipedia.org/wiki/Carnot%27s_theorem_%28thermodynamics%2
9&usg=ALkJrhhjGR0dbJfOPksDTa28M7Vb3TQ7TA
http://en.wikipedia.org/wiki/Thermodynamics
http://translate.googleusercontent.com/translate_c?depth=1&hl=id&langpair=en|id&rurl=transla
te.google.co.id&u=http://en.wikipedia.org/wiki/Pressure&usg=ALkJrhhXCqhmEjd0Yfm_ej3yZ
y0v_-S9nA
http://www.fisikanet.lipi.go.id/utama.cgi?cetakartikel&1112756344
http://didot4com.wordpress.com/animasi-fisika/
http://subkioke.wordpress.com/download/download-animasi-flash/
http://blogfisikaku.wordpress.com/category/animasi-fisika/
http://translate.googleusercontent.com/translate_c?depth=6&hl=id&langpair=en|id&rurl=transla
te.google.com&twu=1&u=http://en.wikipedia.org/wiki/Entropy&usg=ALkJrhiWhhcRmymmct
C6nuXAZgzmds97XQ
http://translate.googleusercontent.com/translate_c?depth=6&hl=id&langpair=en|id&rurl=transla
te.google.com&twu=1&u=http://en.wikipedia.org/wiki/Free_entropy&usg=ALkJrhiD5ZCpKZS
FYSijDSWQuVVlNMW3YQ

68. http://translate.googleusercontent.com/translate_c?depth=6&hl=id&langpair=en|id&rurl=transla
te.google.com&twu=1&u=http://en.wikipedia.org/wiki/Entropy_%28classical_thermodynamics
%29&usg=ALkJrhio3ebSUjZj1zB7FLgwzw48hN0ugA
Latihan Soal
Soal No. 1
Suatu gas memiliki volume awal 2,0 m3
dipanaskan dengan kondisi isobaris hingga volume
akhirnya menjadi 4,5 m3
. Jika tekanan gas adalah 2 atm, tentukan usaha luar gas tersebut!
(1 atm = 1,01 x 105
Pa)
Pembahasan
Data :
V2 = 4,5 m3
V1 = 2,0 m3
P = 2 atm = 2,02 x 105
Pa
Isobaris → Tekanan Tetap
W = P (ΔV)
W = P(V2 − V1)
W = 2,02 x 105
(4,5 − 2,0) = 5,05 x 105
joule
Soal No. 2
1,5 m3
gas helium yang bersuhu 27o
C dipanaskan secara isobarik sampai 87o
C. Jika tekanan gas
helium 2 x 105
N/m2
, gas helium melakukan usaha luar sebesar….
A. 60 kJ
B. 120 kJ
C. 280 kJ
D. 480 kJ
E. 660 kJ
(Sumber Soal : UMPTN 1995)
Pembahasan
Data :
V1 = 1,5 m3
T1 = 27o
C = 300 K
T2 = 87o
C = 360 K
P = 2 x 105
N/m2

69. W = PΔV
Mencari V2 :
V
2/T2 = V
1/T1
V2 = ( V
1/T1 ) x T2 = ( 1,5
/300 ) x 360 = 1,8 m3
W = PΔV = 2 x 105
(1,8 − 1,5) = 0,6 x 105
= 60 x 103
= 60 kJ
Soal No. 3
2000
/693 mol gas helium pada suhu tetap 27o
C mengalami perubahan volume dari 2,5 liter
menjadi 5 liter. Jika R = 8,314 J/mol K dan ln 2 = 0,693 tentukan usaha yang dilakukan gas
helium!
Pembahasan
Data :
n = 2000
/693 mol
V2 = 5 L
V1 = 2,5 L
T = 27o
C = 300 K
Usaha yang dilakukan gas :
W = nRT ln (V2 / V1)
W = (2000
/693 mol) ( 8,314 J/mol K)(300 K) ln ( 5 L
/ 2,5 L )
W = (2000
/693) (8,314) (300) (0,693) = 4988,4 joule
Soal No. 4
Mesin Carnot bekerja pada suhu tinggi 600 K, untuk menghasilkan kerja mekanik. Jika mesin
menyerap kalor 600 J dengan suhu rendah 400 K, maka usaha yang dihasilkan adalah….
A. 120 J
B. 124 J
C. 135 J
D. 148 J
E. 200 J
(Sumber Soal : UN Fisika 2009 P04 No. 18)
Pembahasan
η = ( 1 − T
r / Tt ) x 100 %
Hilangkan saja 100% untuk memudahkan perhitungan :
η = ( 1 − 400
/600) = 1
/3
η = ( W
/ Q1 )
1
/3 = W
/600
W = 200 J
Soal No. 5
Diagram P−V dari gas helium yang mengalami proses termodinamika ditunjukkan seperti
gambar berikut!

70. Usaha yang dilakukan gas helium pada proses ABC sebesar….
A. 660 kJ
B. 400 kJ
C. 280 kJ
D. 120 kJ
E. 60 kJ
(Sumber Soal : UN Fisika 2010 P04 No. 17)
Pembahasan
WAC = WAB + WBC
WAC = 0 + (2 x 105
)(3,5 − 1,5) = 4 x 105
= 400 kJ
Soal No. 6
Suatu mesin Carnot, jika reservoir panasnya bersuhu 400 K akan mempunyai efisiensi 40%. Jika
reservoir panasnya bersuhu 640 K, efisiensinya…..%
A. 50,0
B. 52,5
C. 57,0
D. 62,5
E. 64,0
(Sumber Soal : SPMB 2004)
Pembahasan
Data pertama:
η = 40% = 4
/ 10
Tt = 400 K
Cari terlebih dahulu suhu rendahnya (Tr) hilangkan 100 % untuk mempermudah perhitungan:
η = 1 − (Tr
/Tt)
4
/ 10 = 1 − (Tr
/400)
(Tr
/400) = 6
/ 10
Tr = 240 K
Data kedua :
Tt = 640 K
Tr = 240 K (dari hasil perhitungan pertama)
η = ( 1 − Tr
/Tt) x 100%
η = ( 1 − 240
/640) x 100%
η = ( 5
/ 8 ) x 100% = 62,5%
Soal No. 7
Perhatikan gambar berikut ini!
Jika kalor yang diserap reservoir suhu tinggi adalah 1200 joule, tentukan :
a) Efisiensi mesin Carnot

71. b) Usaha mesin Carnot
c) Perbandingan kalor yang dibuang di suhu rendah dengan usaha yang dilakukan mesin Carnot
d) Jenis proses ab, bc, cd dan da
Pembahasan
a) Efisiensi mesin Carnot
Data :
Tt = 227o
C = 500 K
Tr = 27o
C = 300 K
η = ( 1 − Tr
/Tt) x 100%
η = ( 1 − 300
/500) x 100% = 40%
b) Usaha mesin Carnot
η = W
/Q1
4
/10 = W
/1200
W = 480 joule
c) Perbandingan kalor yang dibuang di suhu rendah dengan usaha yang dilakukan mesin Carnot
Q2 = Q1 − W = 1200 − 480 = 720 joule
Q2 : W = 720 : 480 = 9 : 6 = 3 : 2
d) Jenis proses ab, bc, cd dan da
ab → pemuaian isotermis (volume gas bertambah, suhu gas tetap)
bc → pemuaian adiabatis (volume gas bertambah, suhu gas turun)
cd → pemampatan isotermal (volume gas berkurang, suhu gas tetap)
da → pemampatan adiabatis (volume gas berkurang, suhu gas naik)
Soal No. 8
Suatu gas ideal mengalami proses siklus seperti pada gambar P − V di atas. Kerja yang
dihasilkan pada proses siklus ini adalah….kilojoule.
A. 200
B. 400
C. 600
D. 800
E. 1000
Pembahasan
W = Usaha (kerja) = Luas kurva siklus = Luas bidang abcda
W = ab x bc
W = 2 x (2 x 105
) = 400 kilojoule