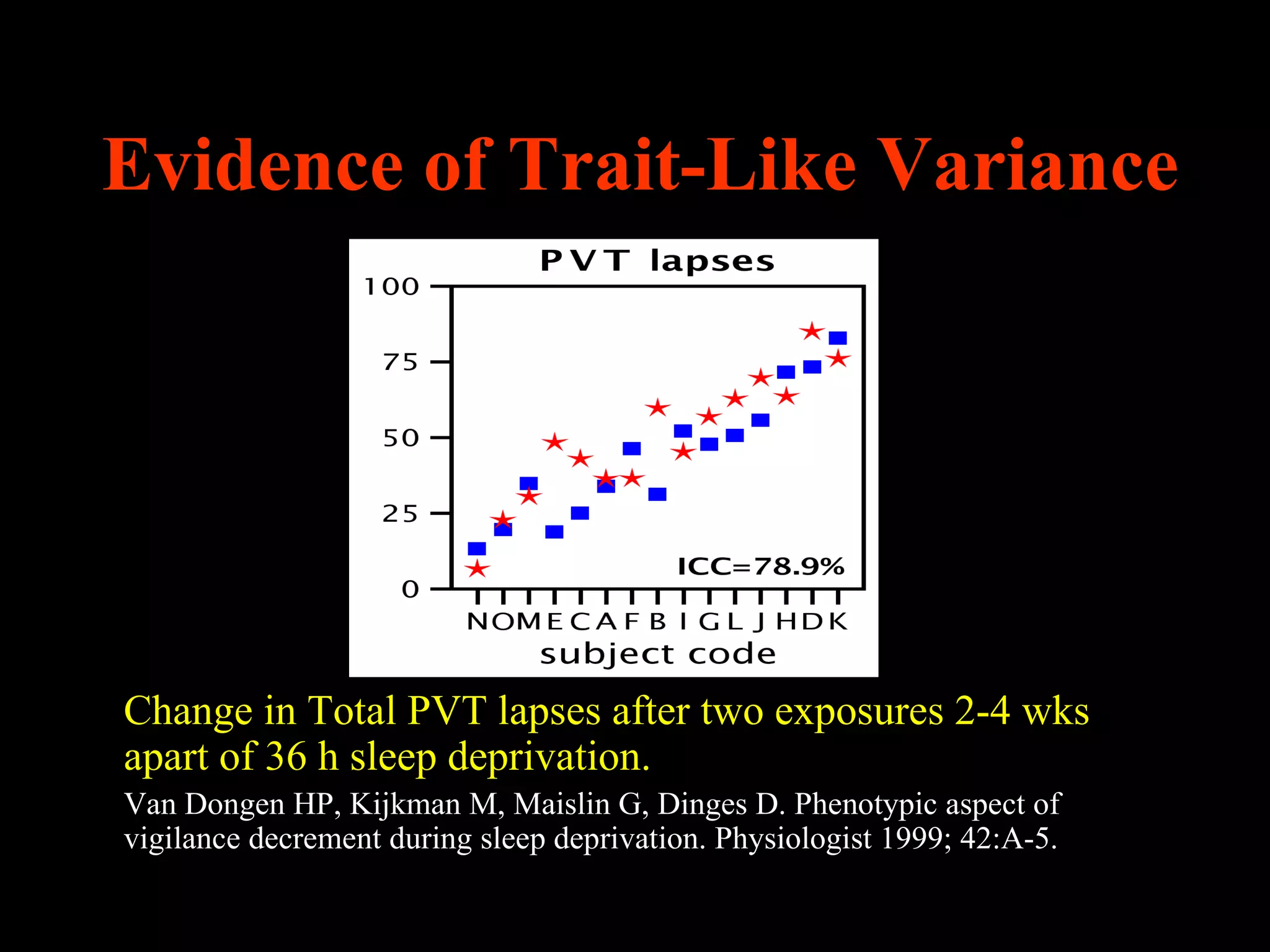
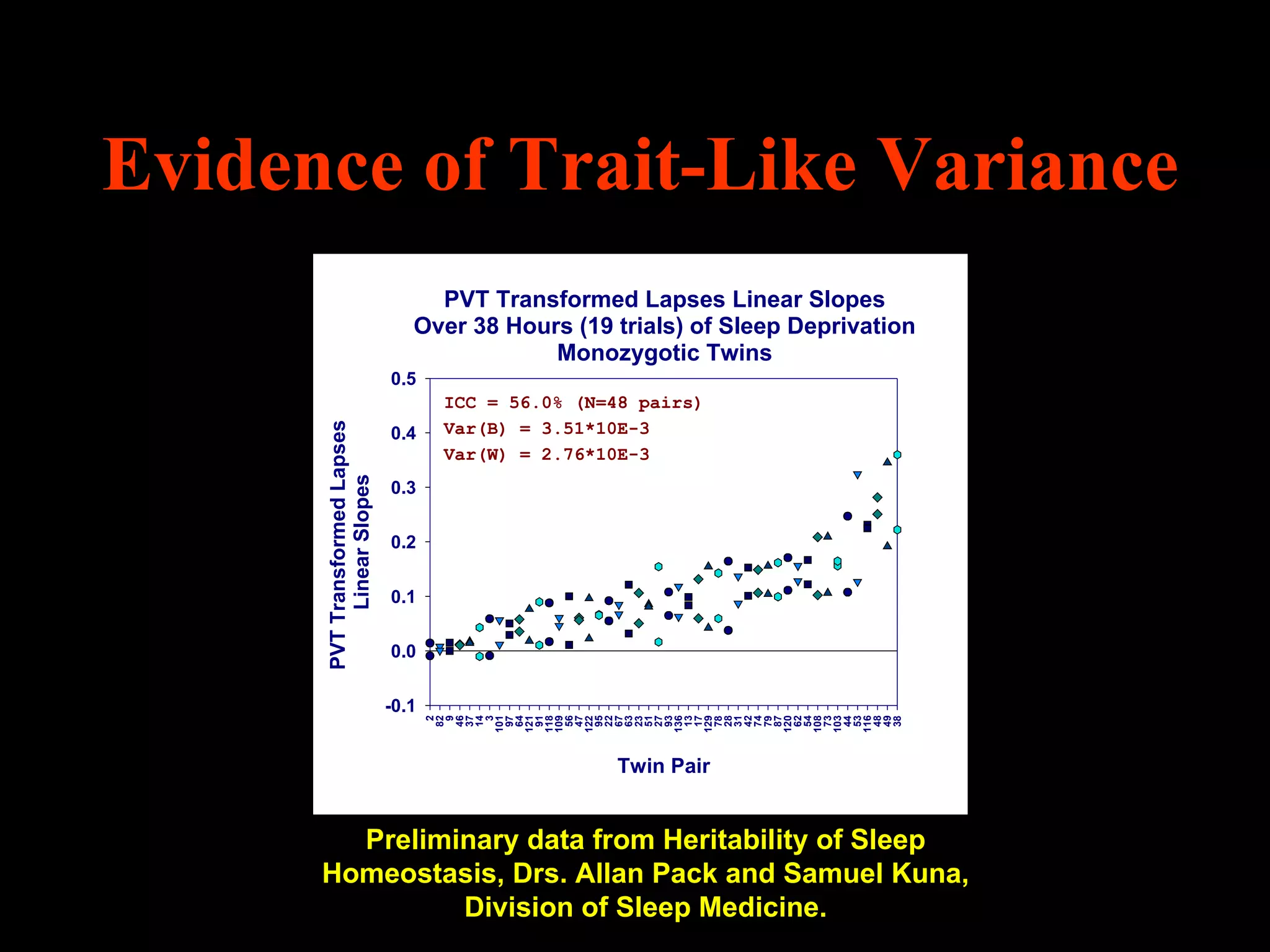
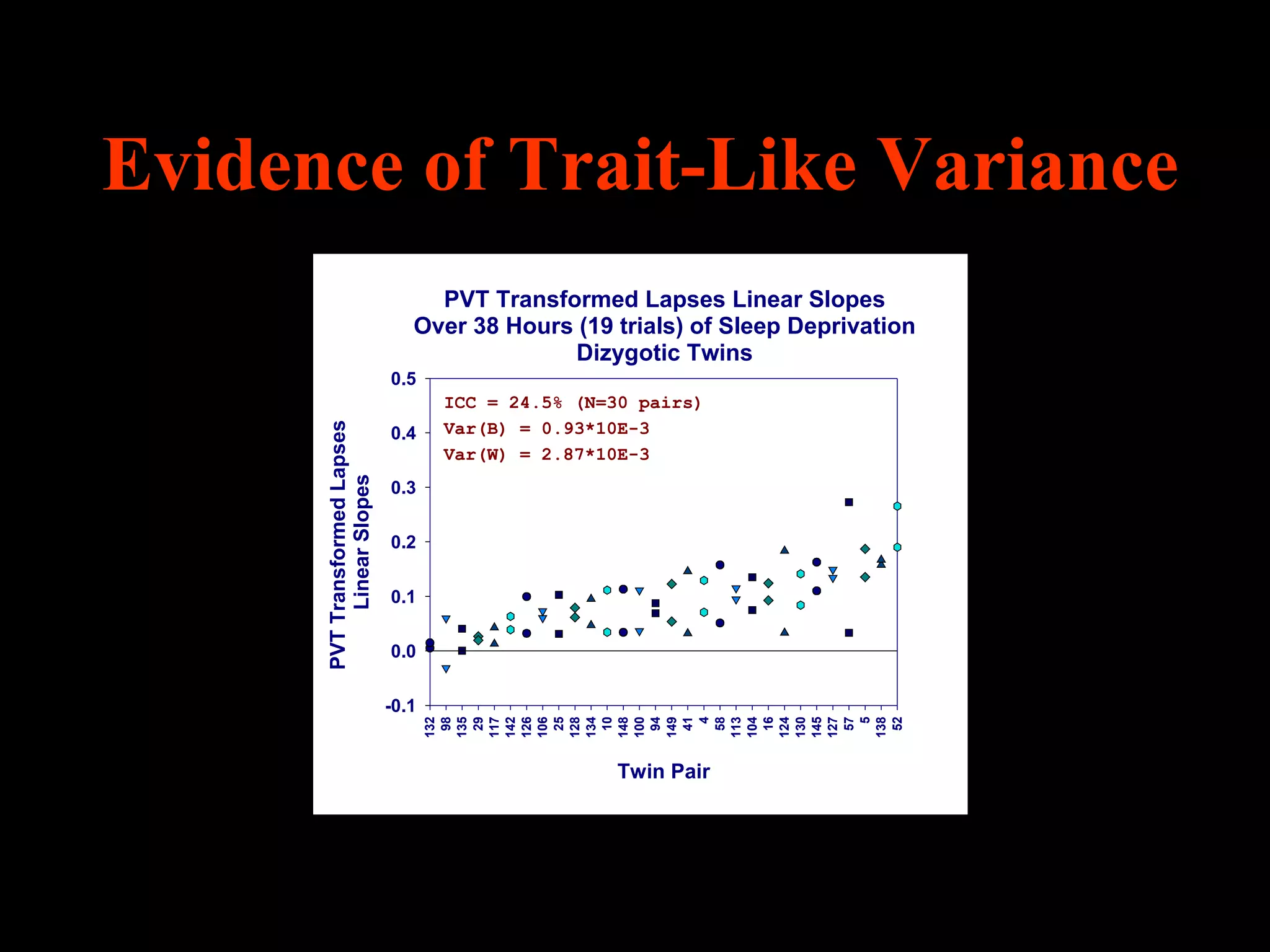
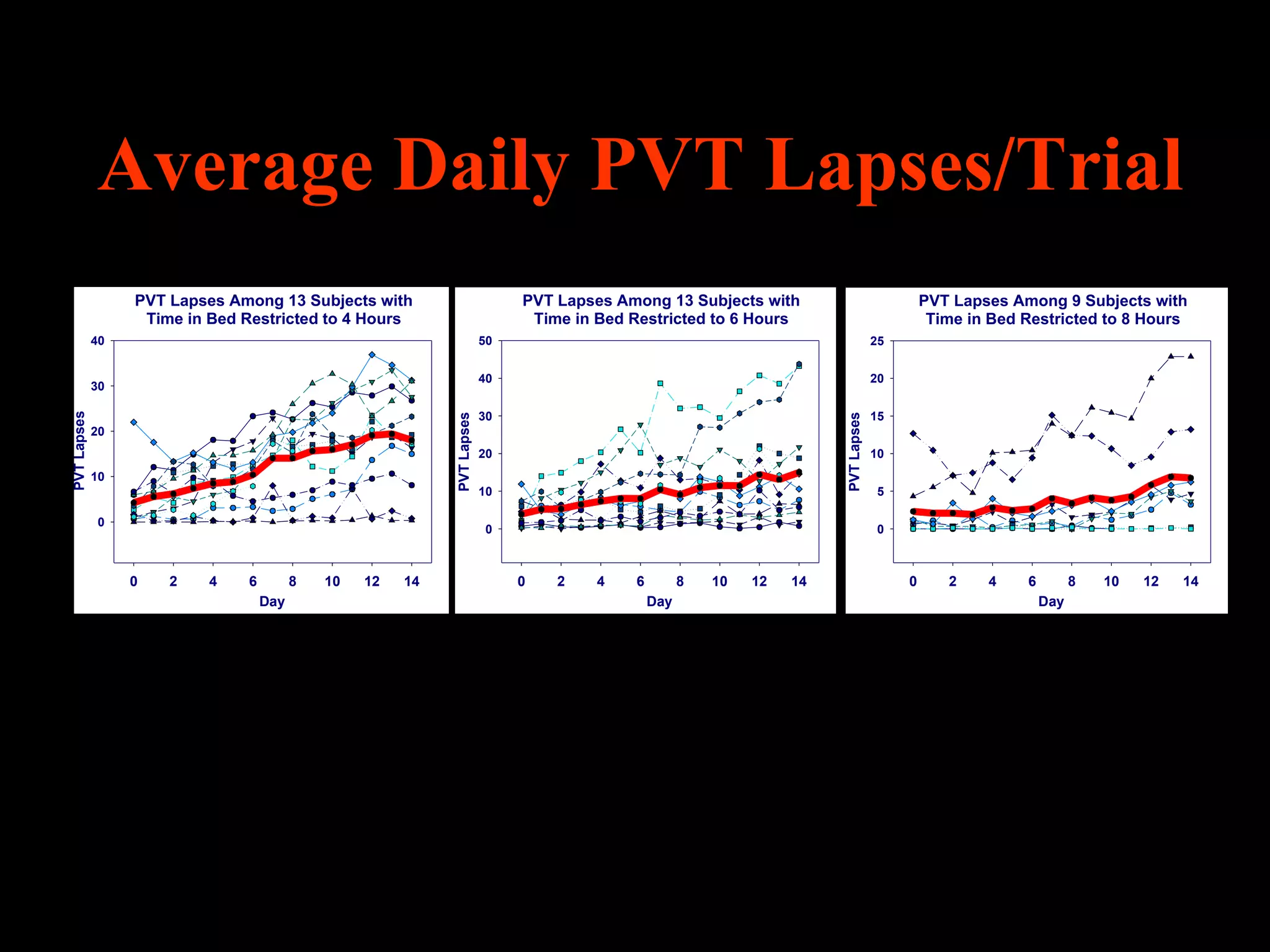
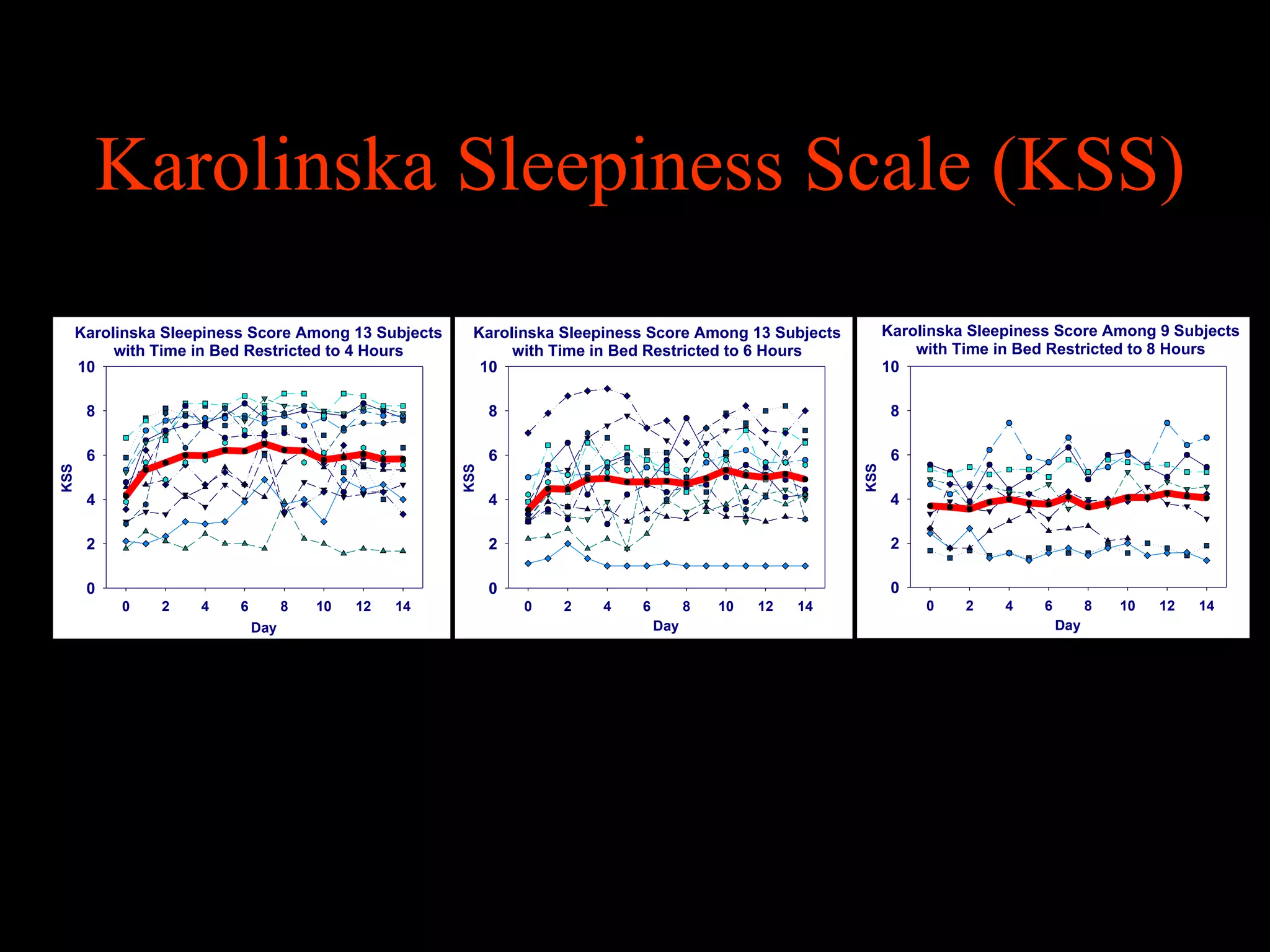
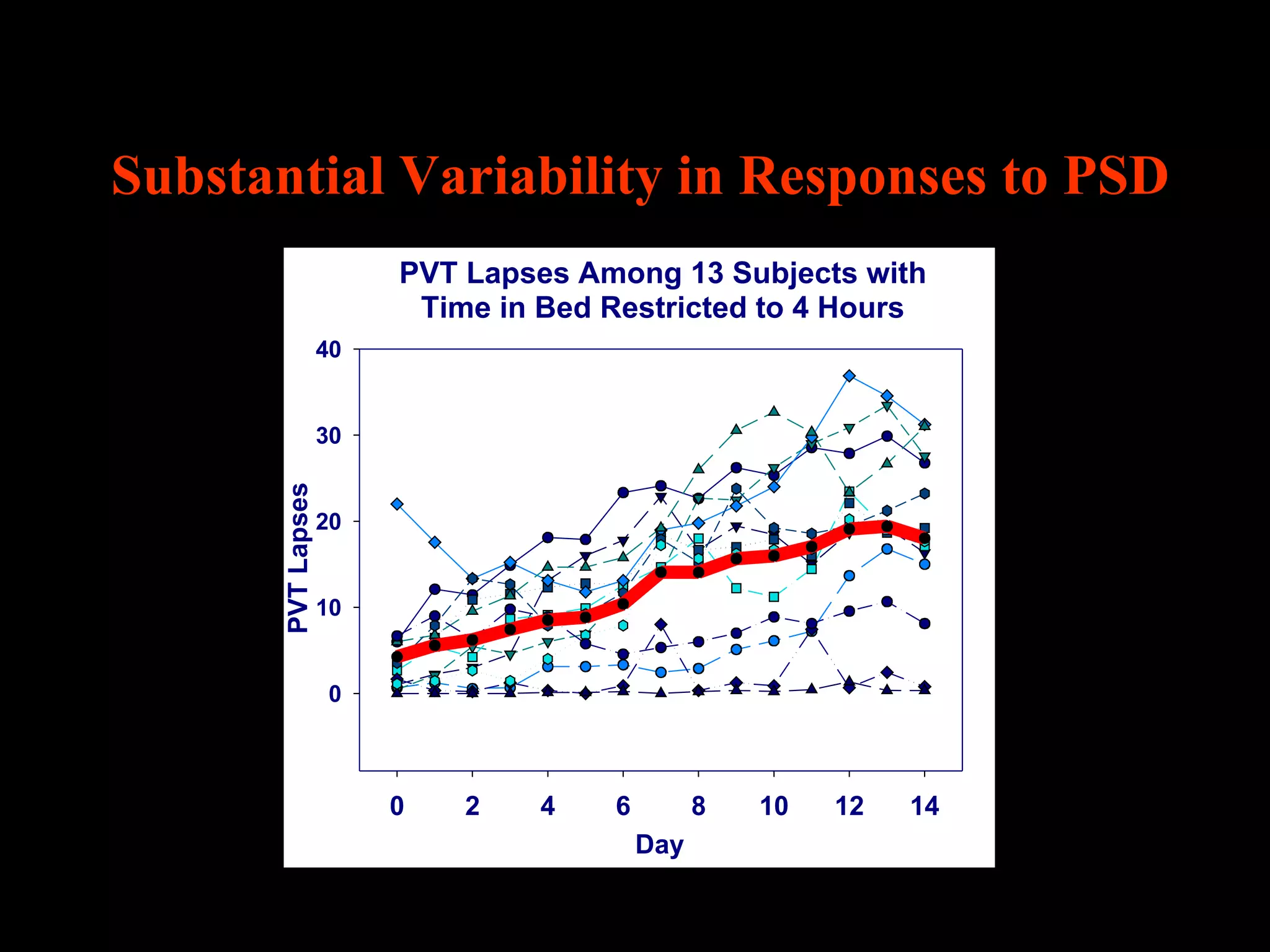
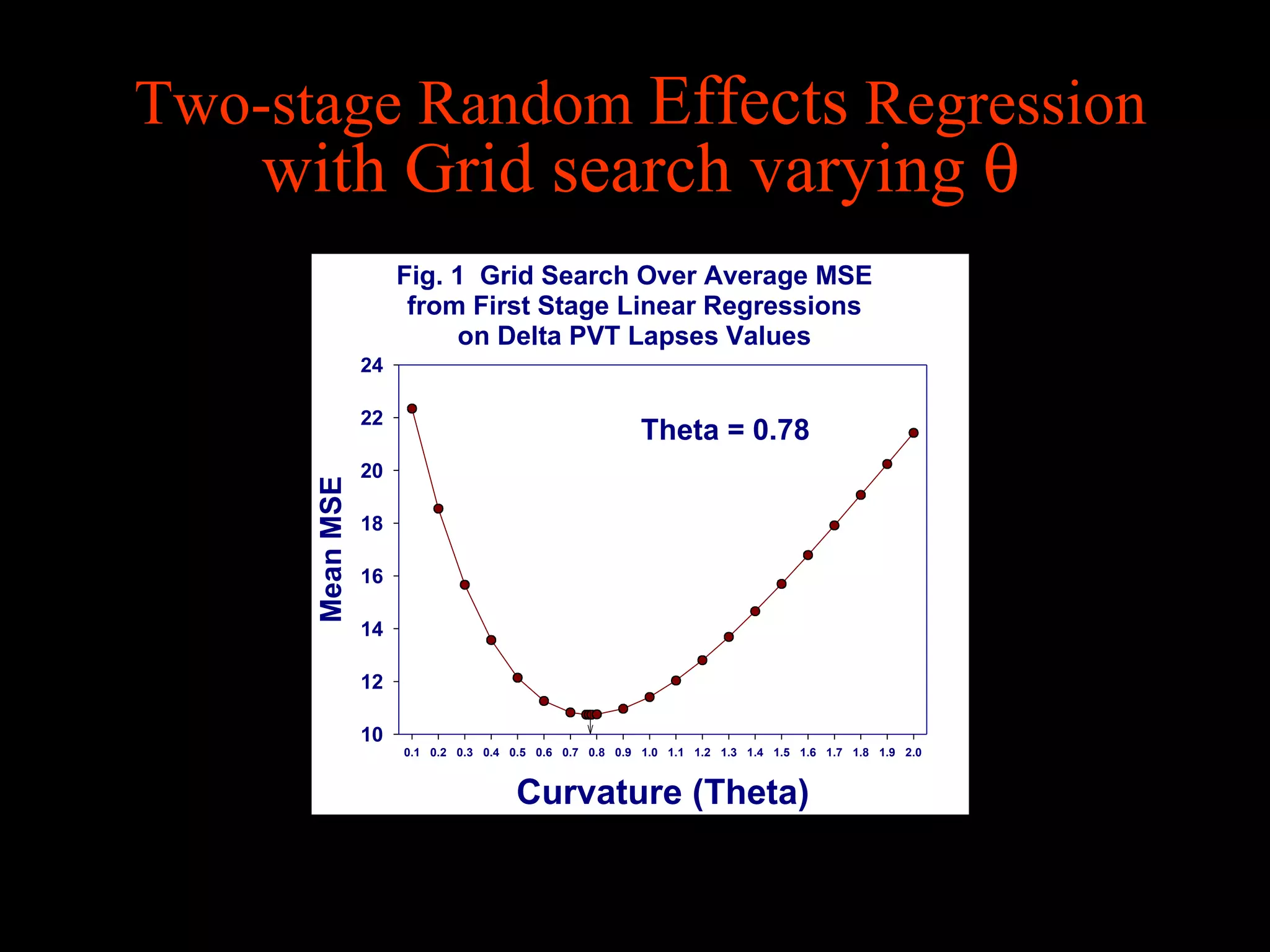
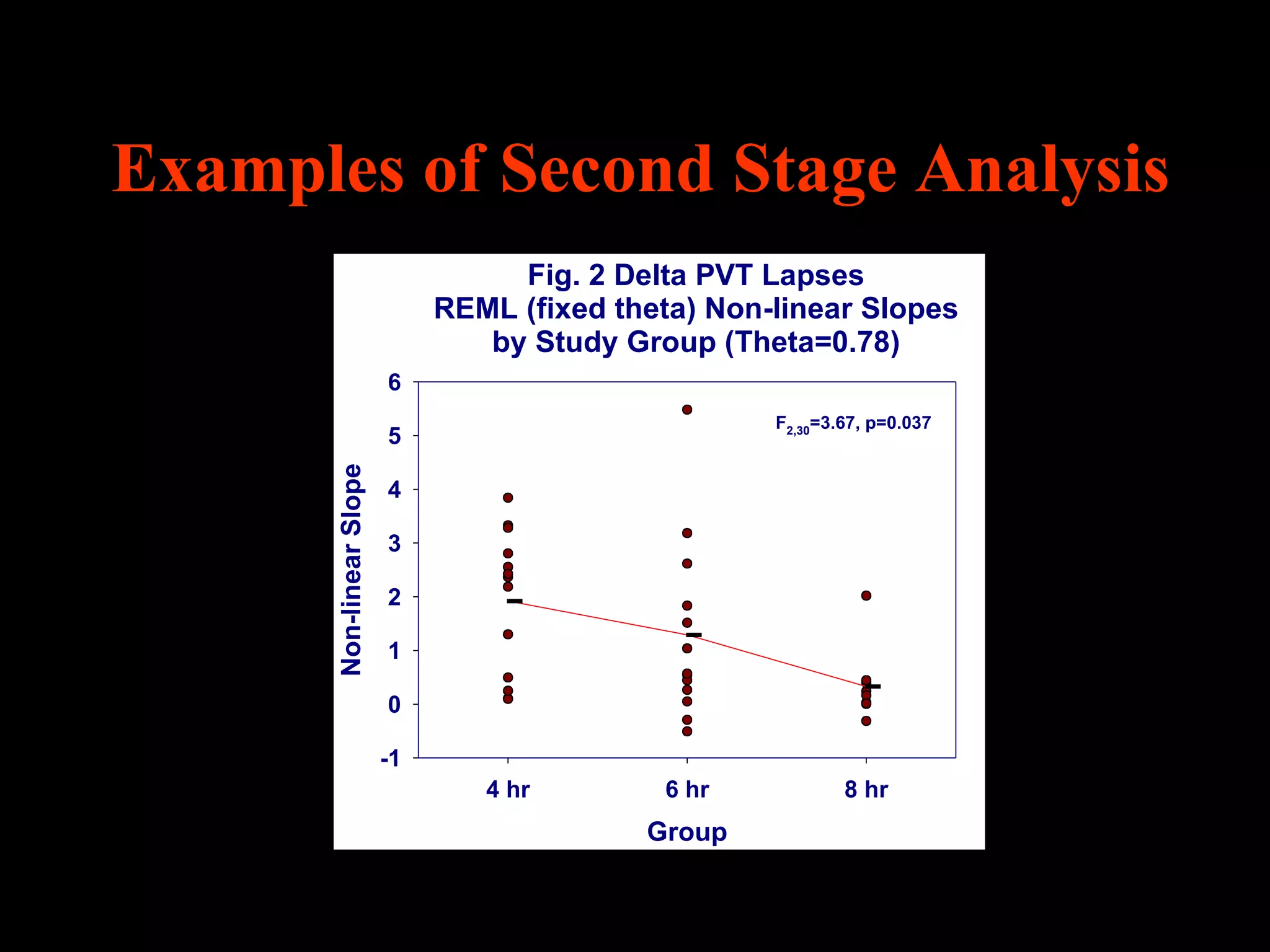
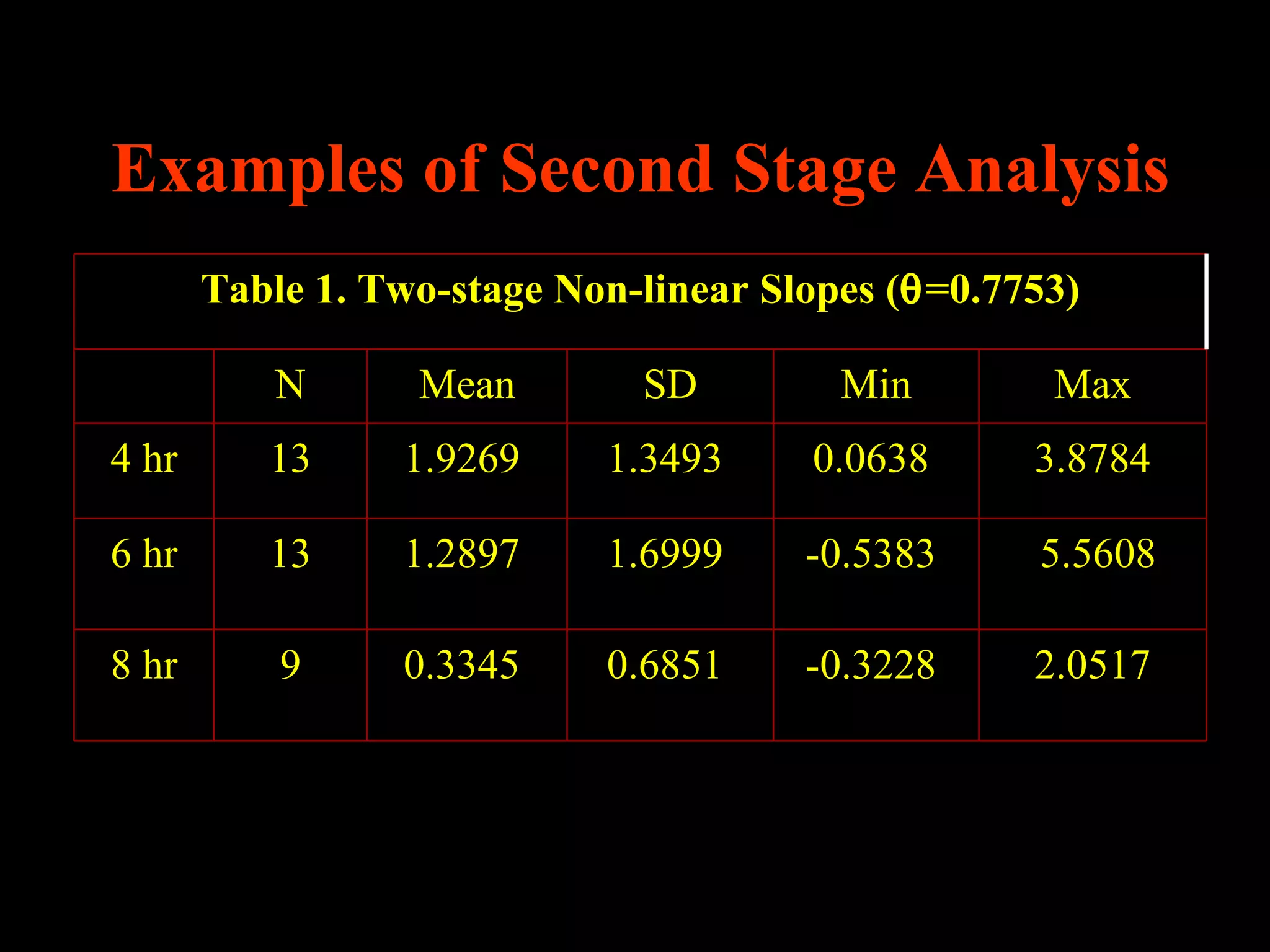
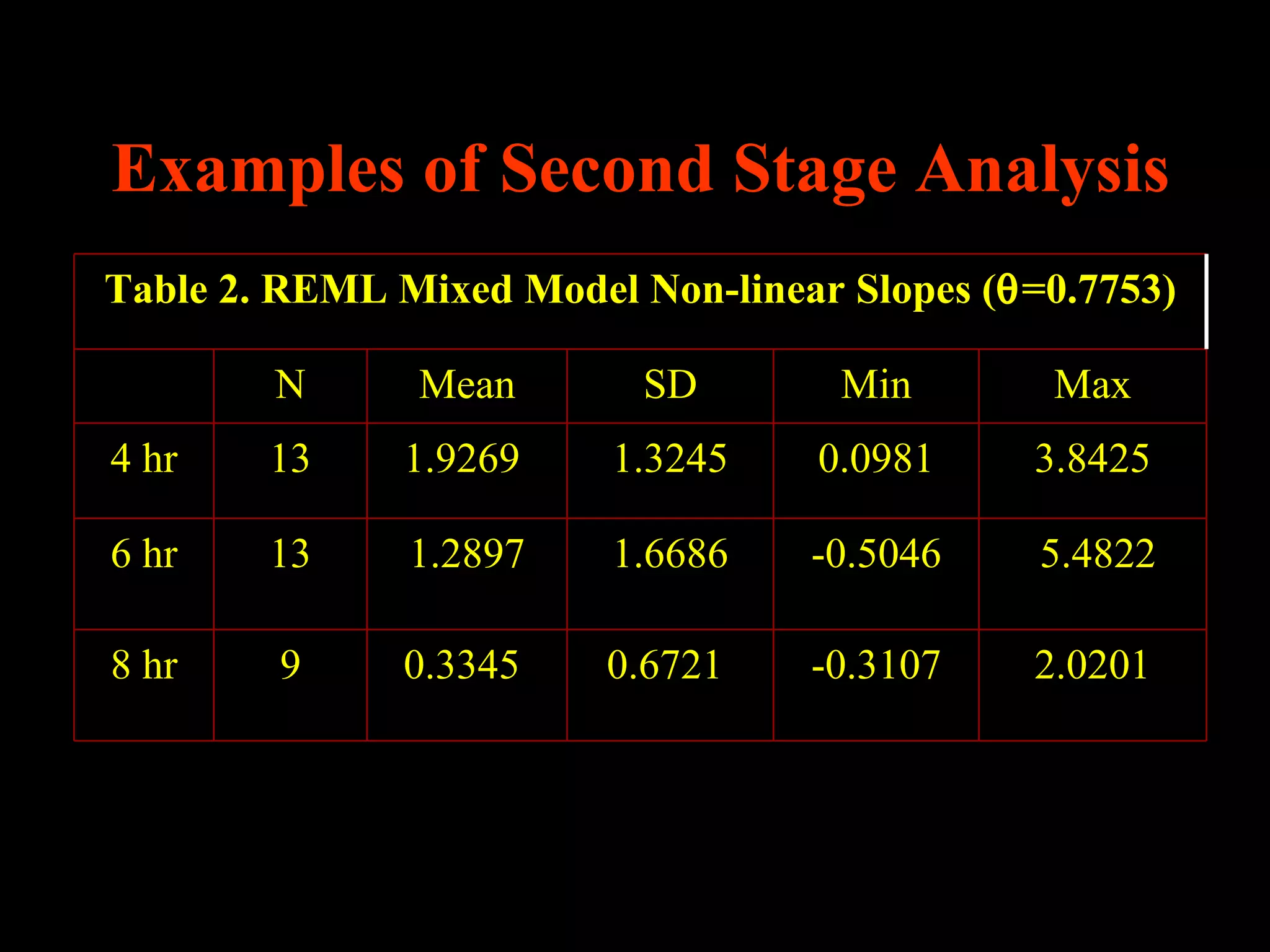
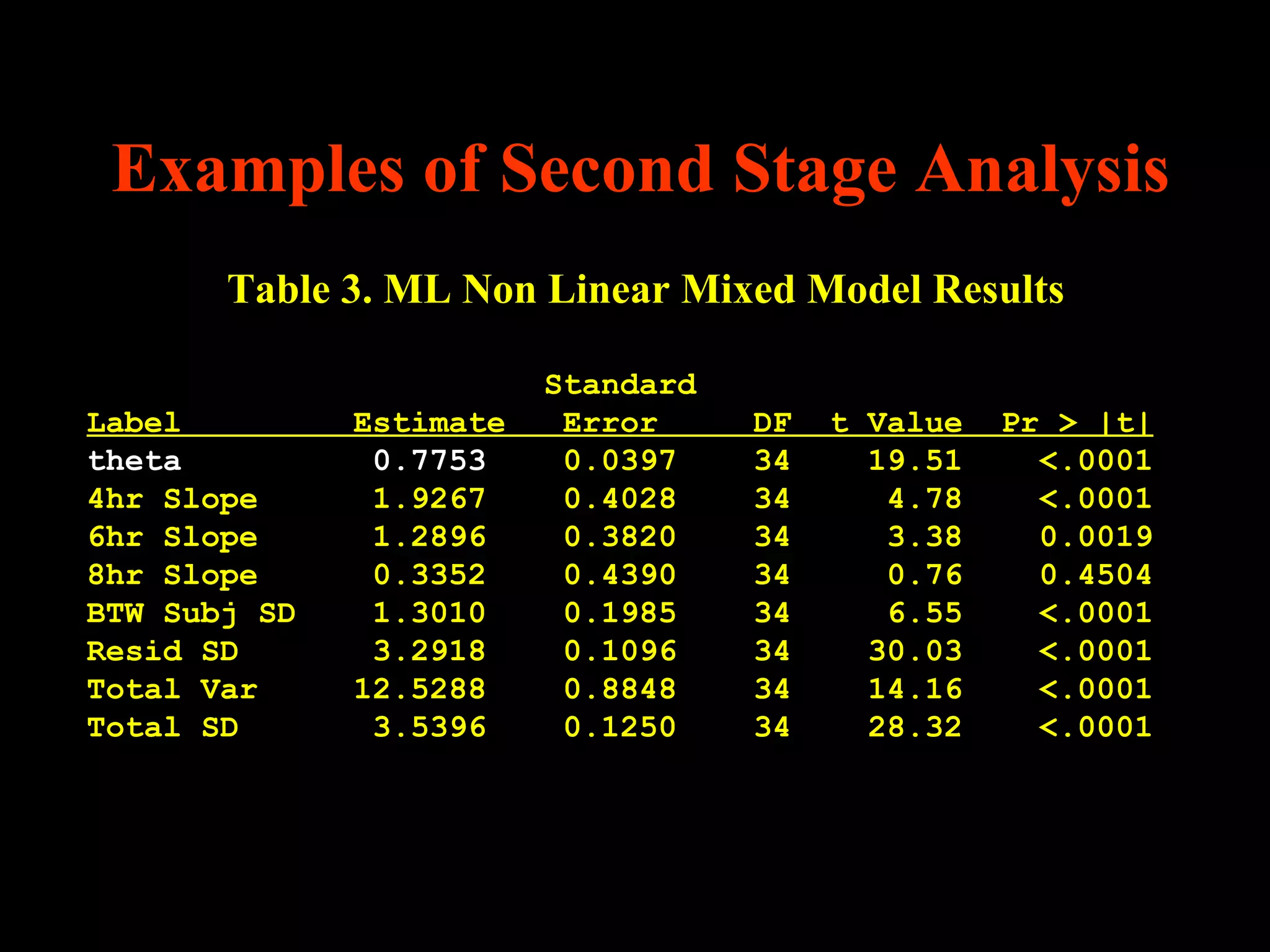
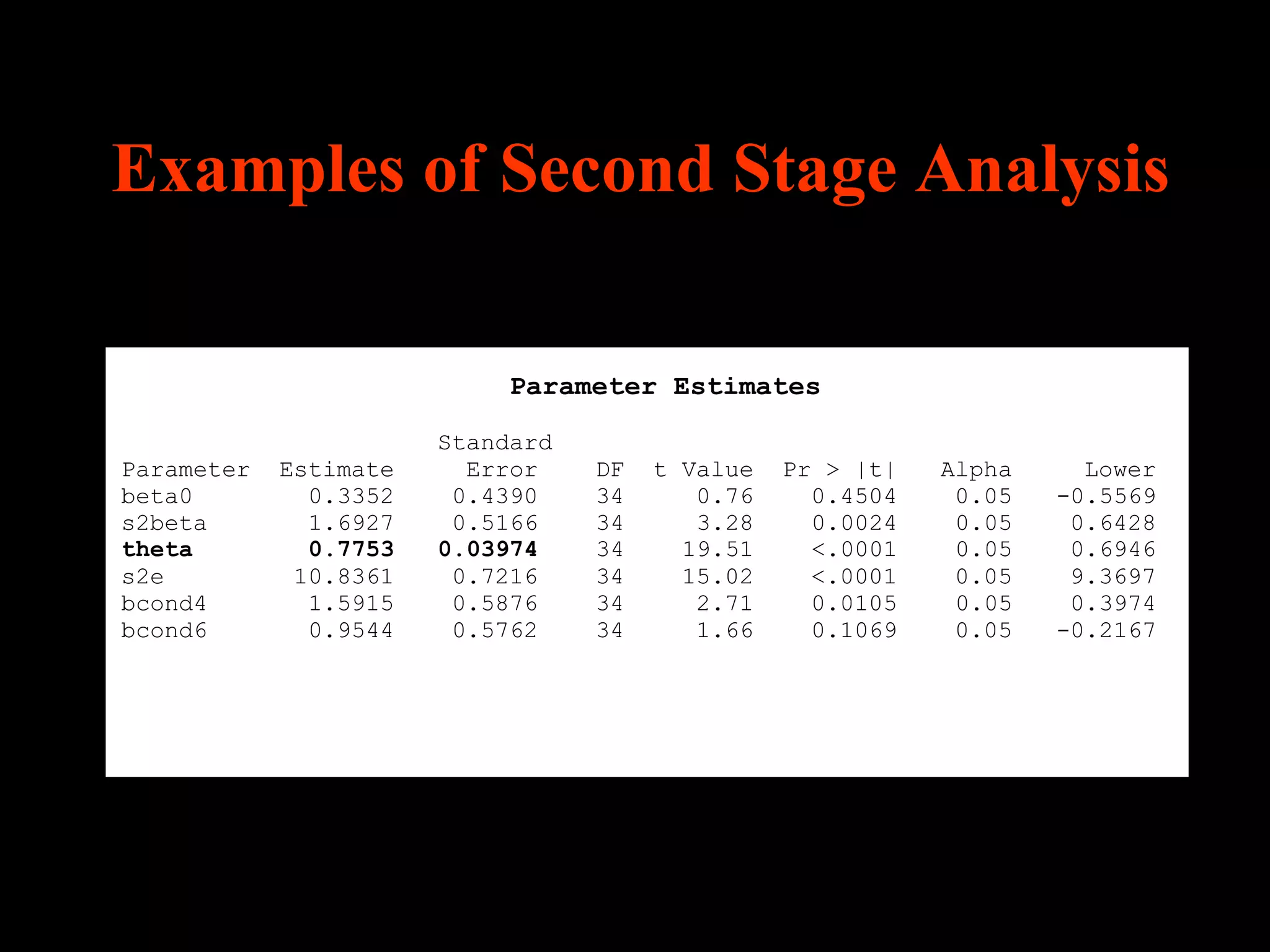
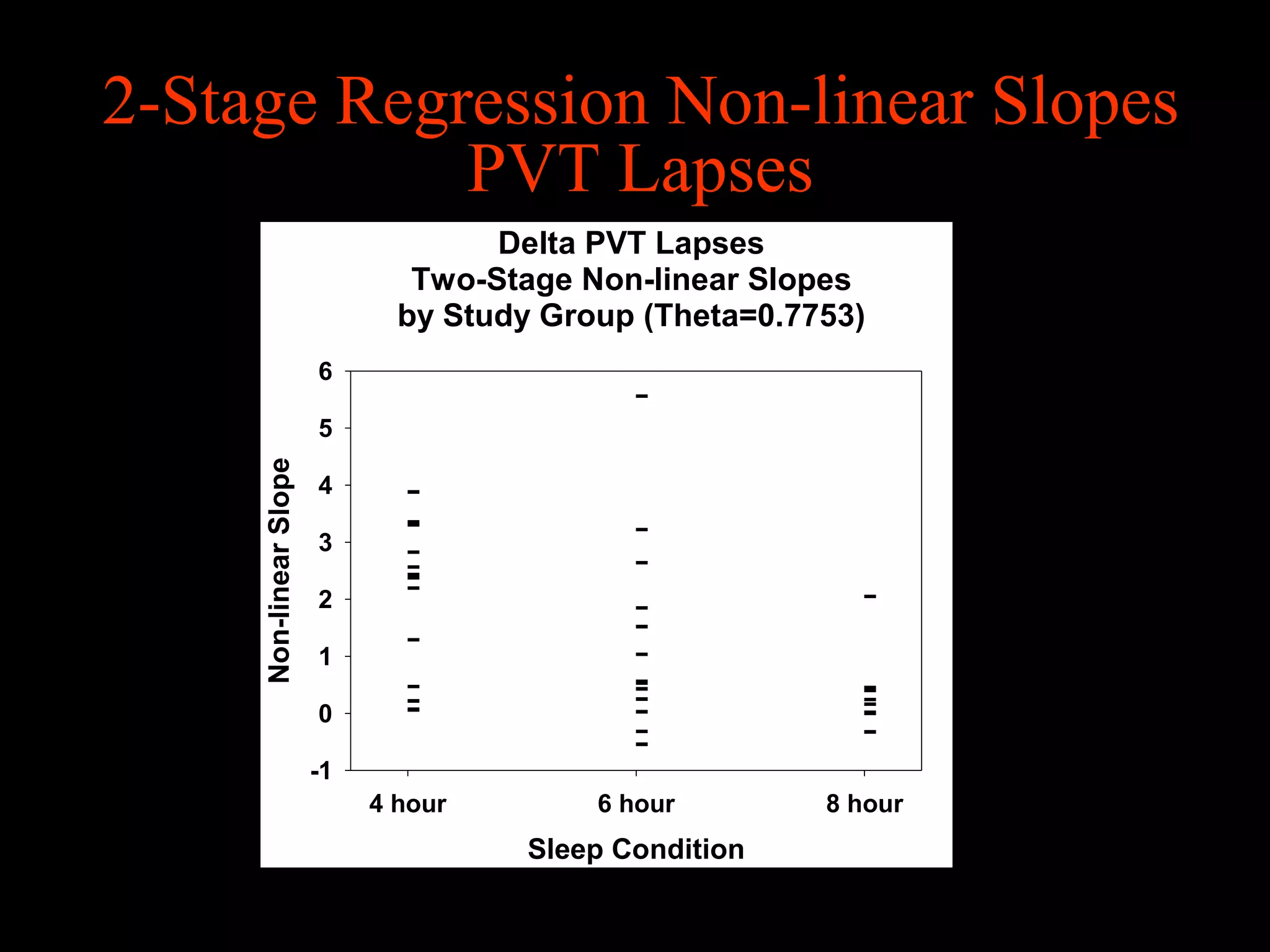
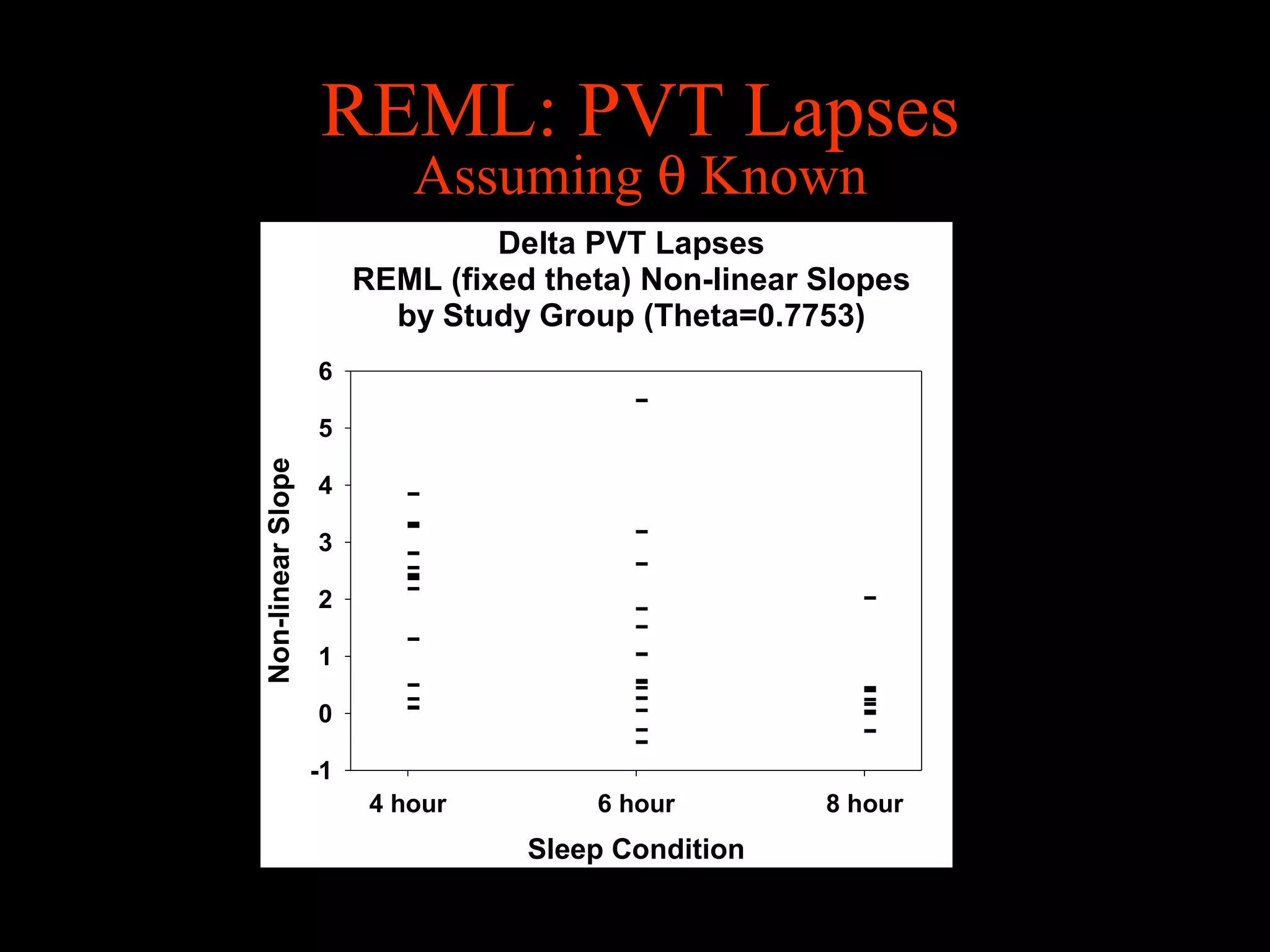
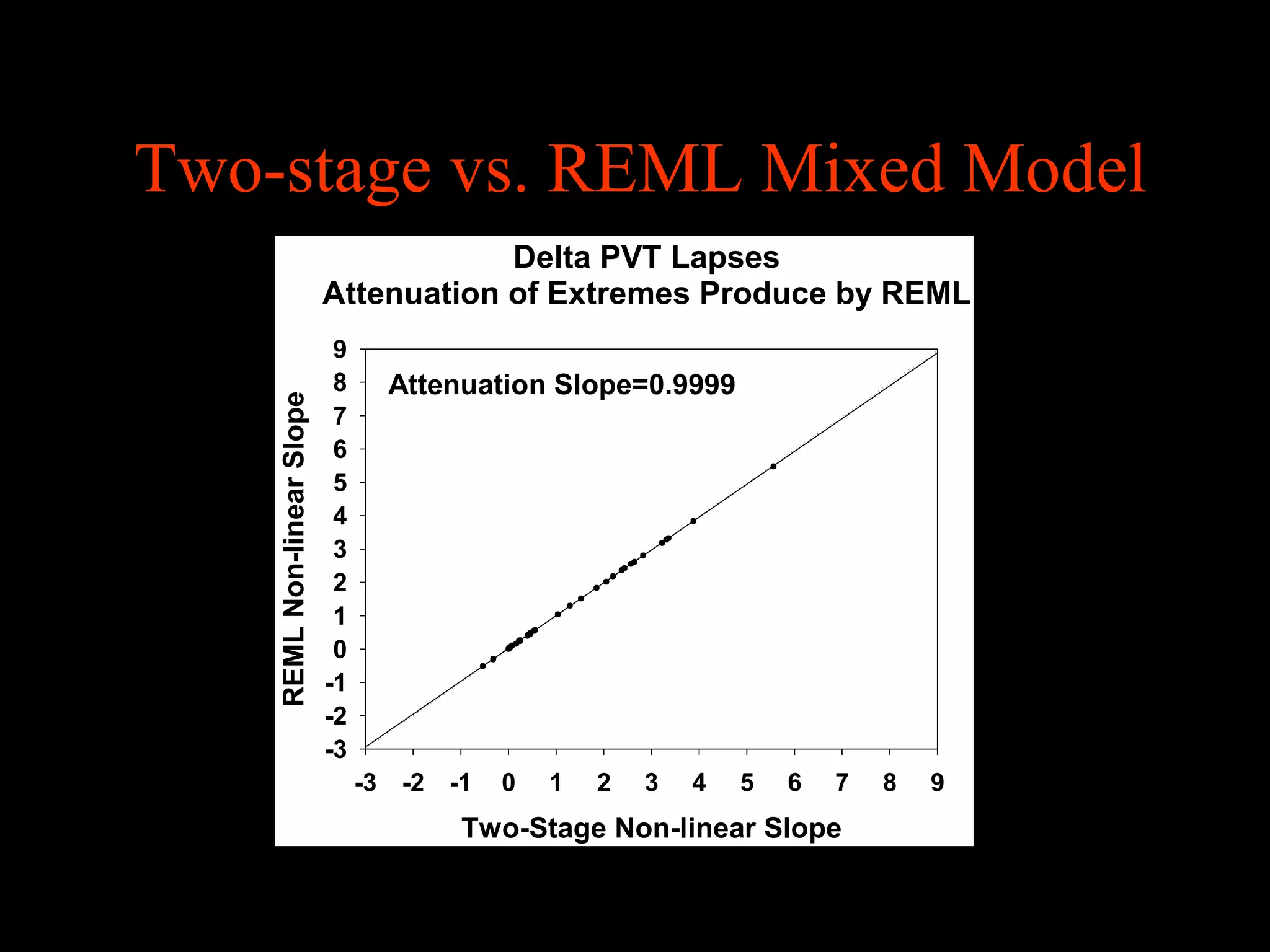
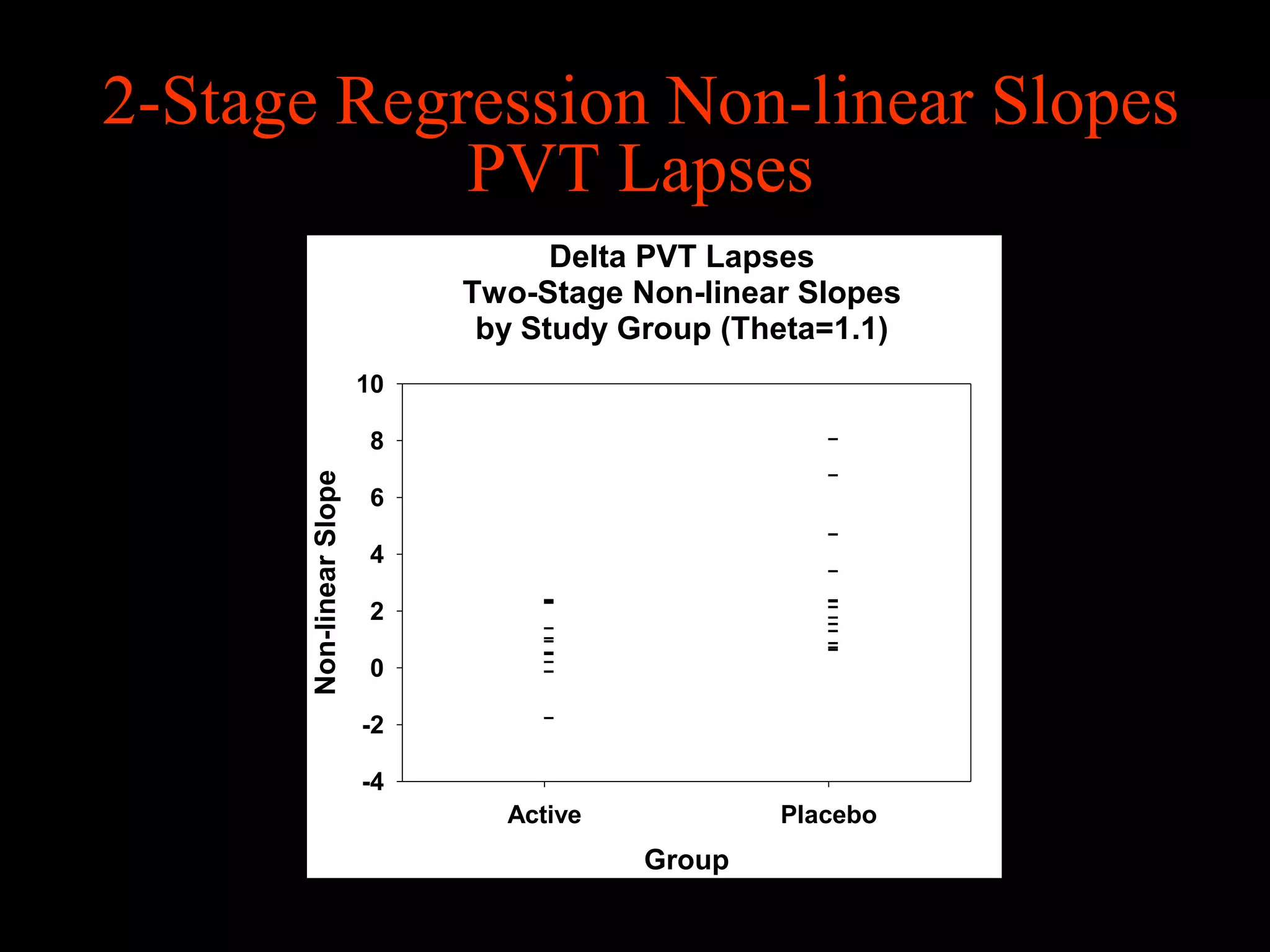
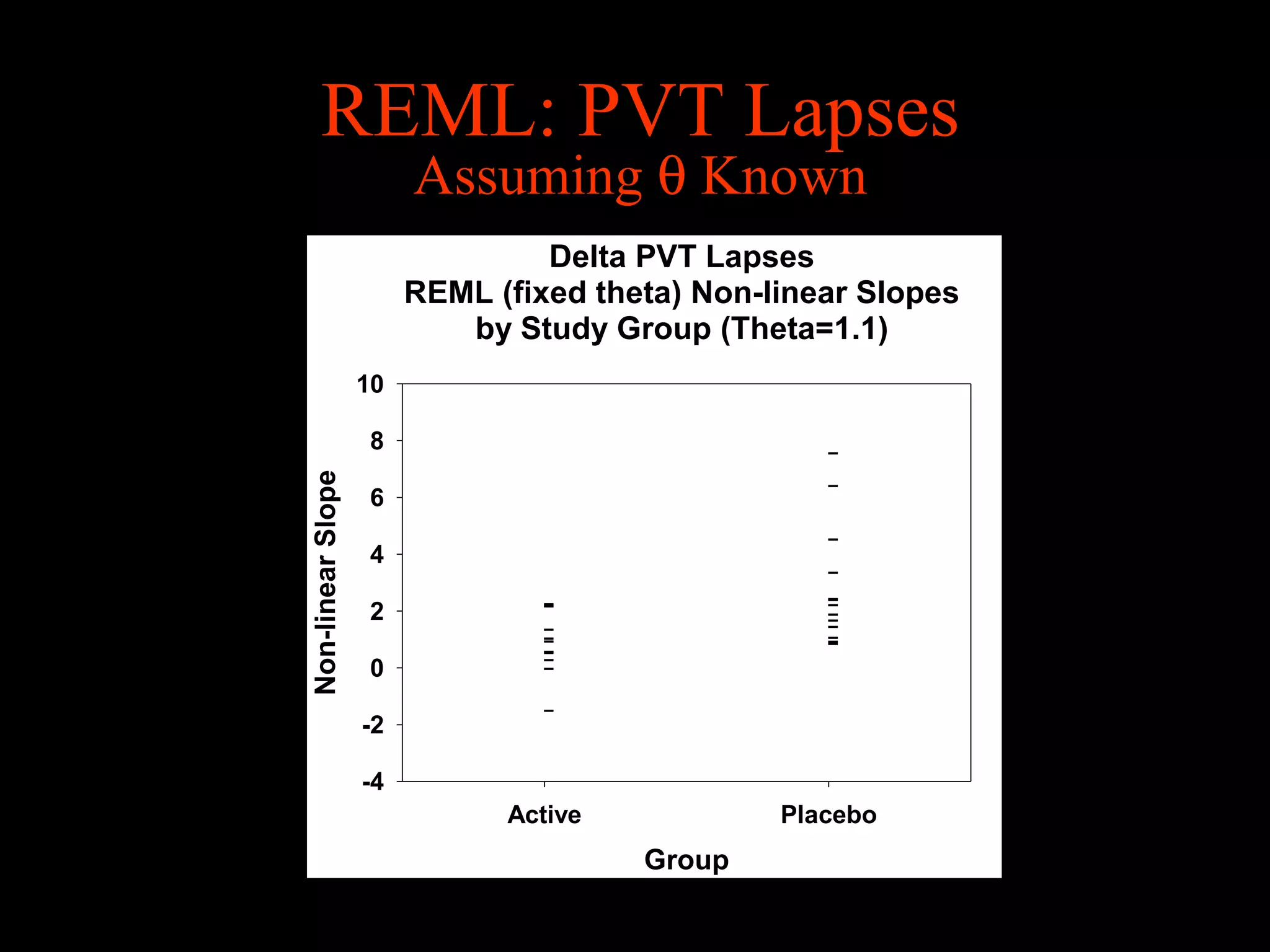
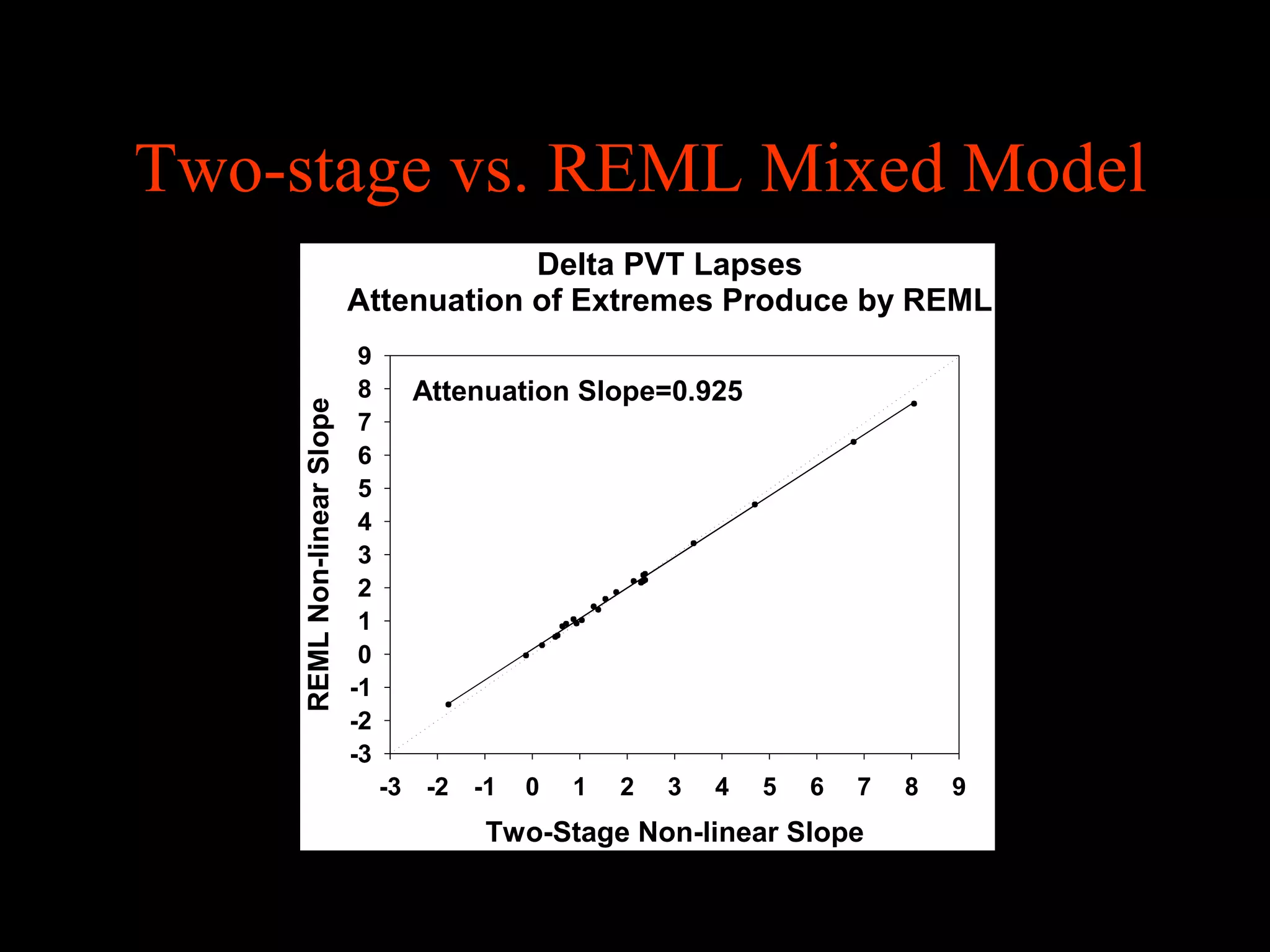
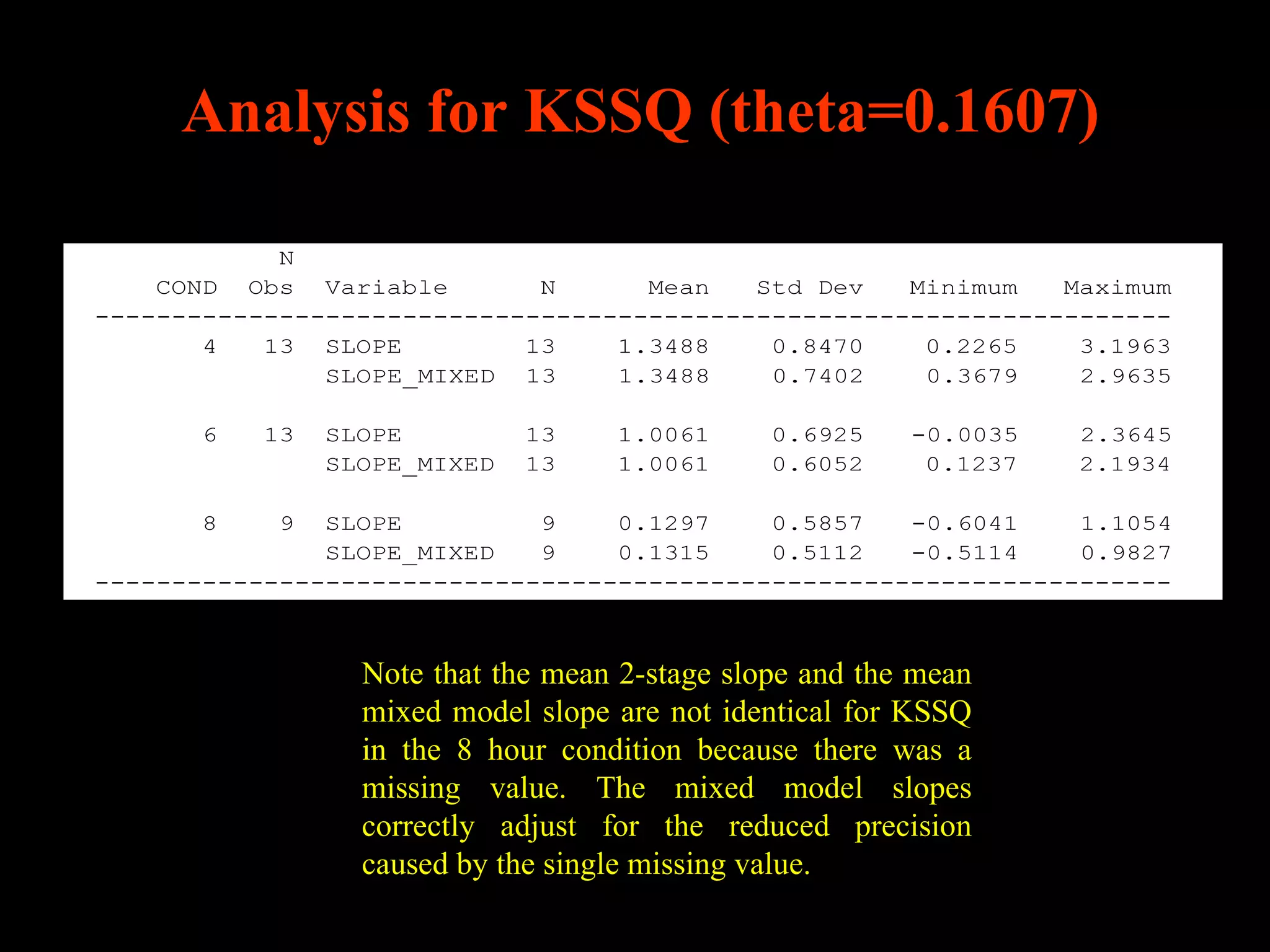
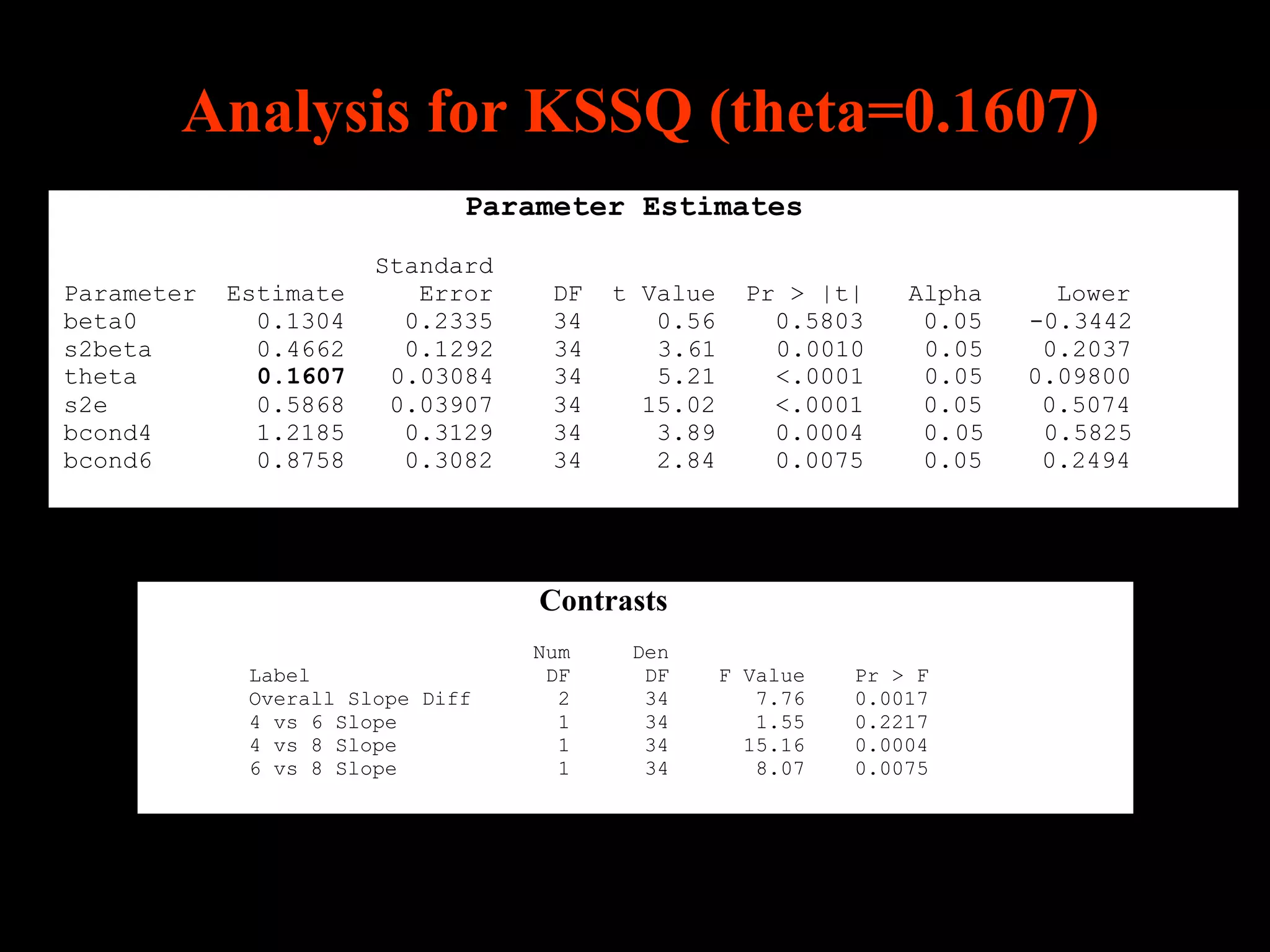
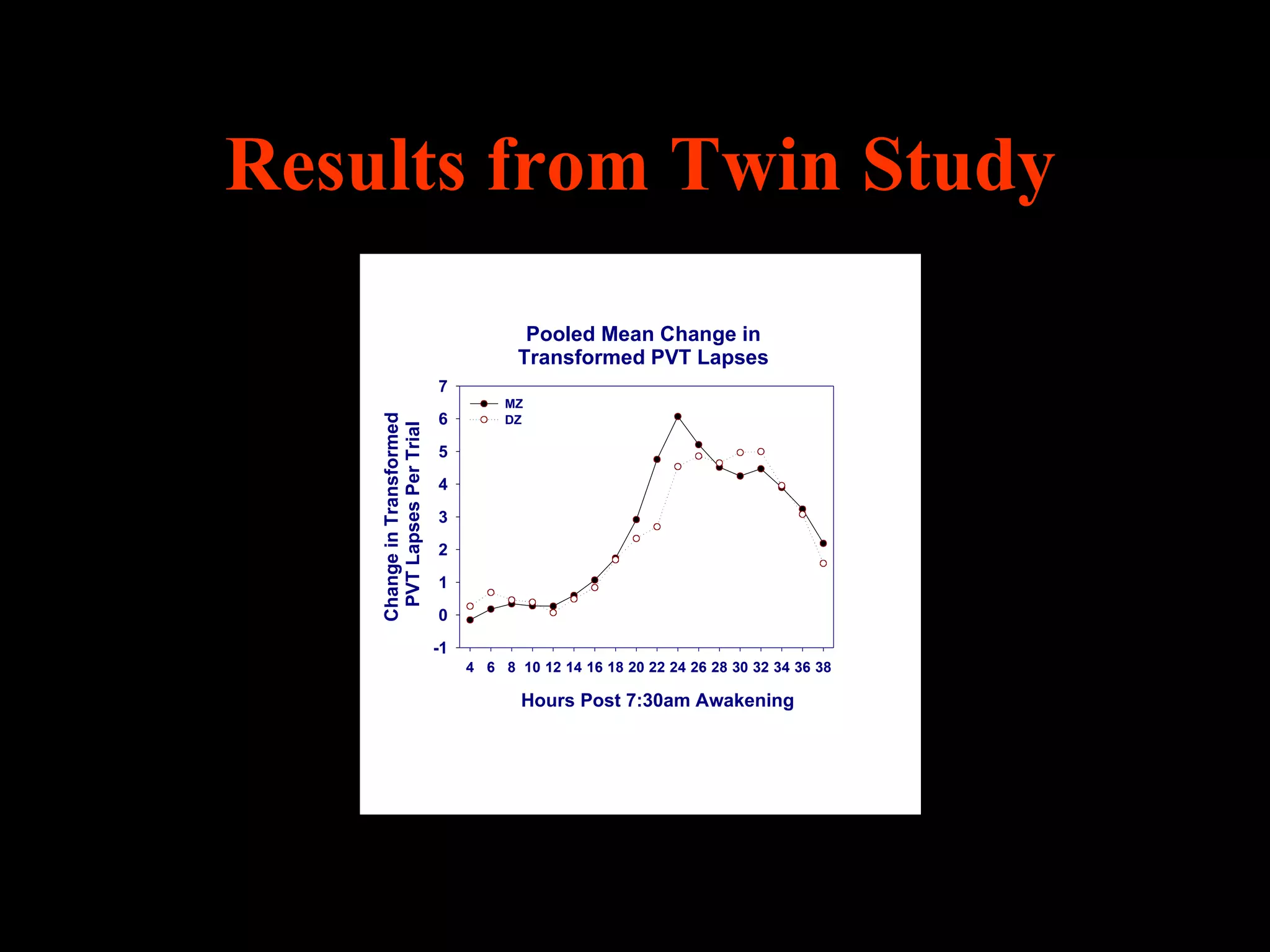
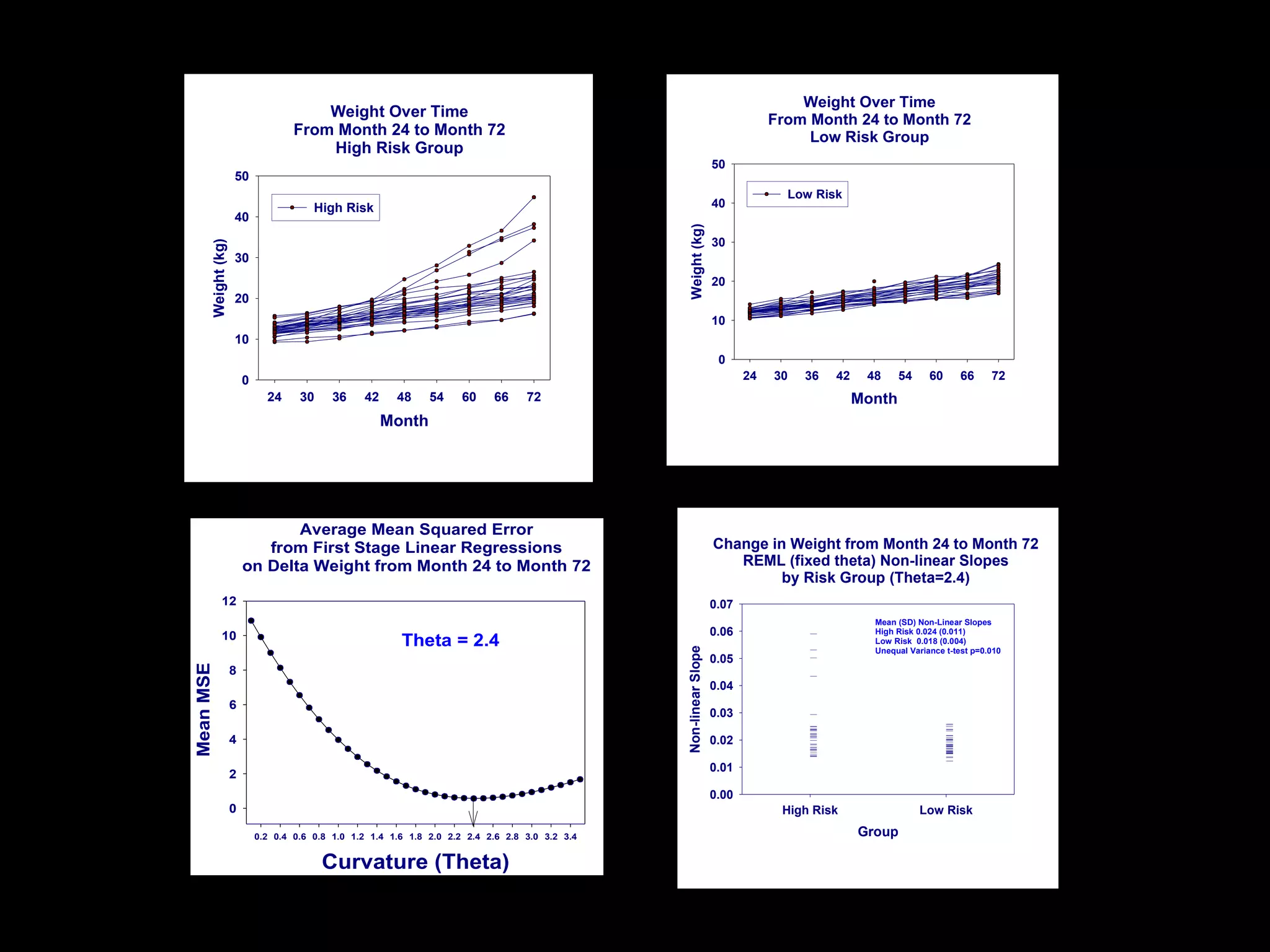
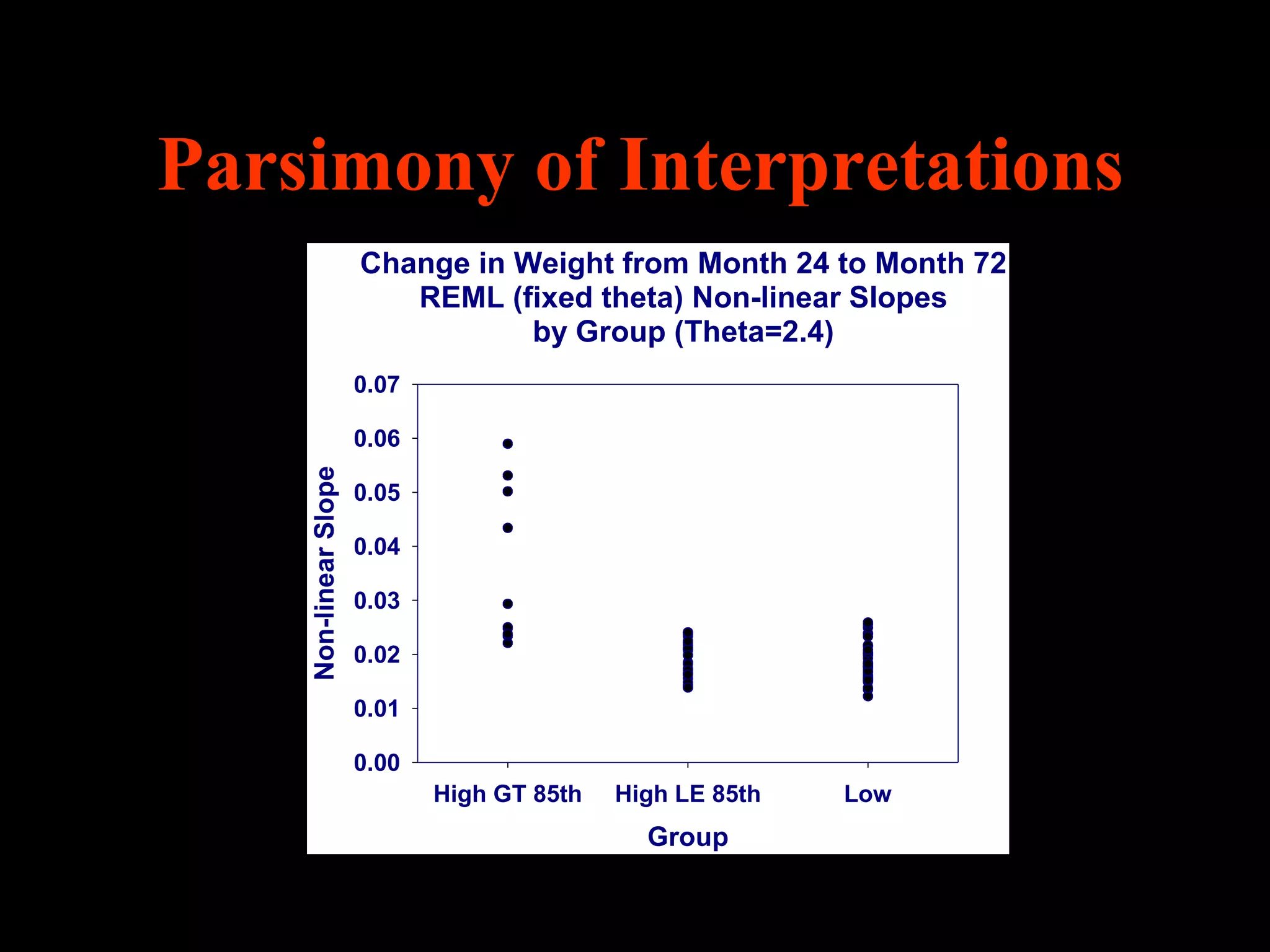
This document discusses statistical approaches for analyzing individual responses to sleep deprivation over time. It presents data from an experiment where subjects had restricted time in bed of 4, 6, or 8 hours for 14 days. Measures like psychomotor vigilance task (PVT) lapses and sleepiness ratings showed substantial variability between subjects. The document proposes a two-stage non-linear mixed model to estimate subject-specific slopes that account for both individual differences and non-linear changes over time. It compares methods like two-stage random effects regression with grid search and maximum likelihood estimation for determining the slopes.

1. Parsimonious Statistical Modeling
of Inter-Individual Response
Differences to Sleep Deprivation
Greg Maislin
Principal Biostatistician
Biomedical Statistical Consulting &
Director, Biostatistics and Data Management Core
Center for Sleep and Respiratory Neurobiology
University of Pennsylvania School of Medicine

2. Acknowledgements and Thanks
 Special thanks to Dr. David F. Dinges whose experiments
exploring the consequences of partial and total sleep
deprivation with and without counter measures provided
fertile ground for deep thinking about some very interesting
statistical issues.
 To Dr. Hans Van Dongen for challenging me to be clear and
compelling in my thinking.
 And to Bob Hachadoorian, Senior Statistical Programmer for
his dedication in programming SAS production runs capable
of mass processing multitudes of assessments across many
domains in the PSD and TSD protocols.

3. Introduction
 Inter-individual differences in response to sleep loss
are substantial. Sleep deprivation protocols often
involve neurobehavioral and physiological testing
over multiple days. There is need for conceptually
simple, yet quantitatively valid statistical methods
that recognize inter-individual variability and
accommodate assay-specific non-linearity of time
trajectories.

4. Intraclass Correlation Coefficient
(ICC)
 Between-subject variance (σbs2 )
 Within-subject (σws2) variance
 σTotal2 = σbs2 + σws2
 ICC is defined as follows to quantify trait-like
inter-individual variability:
 ICC = σbs2
σbs2 + σws2

5. Intraclass Correlation Coefficient
(ICC)
 ICC varies by population since σbs2 varies by
population.
 The magnitudes of σbs2 and σws2 should be
interpreted, not just ICC.
 Mixed effects ANOVA can be used to estimate
ICC-like measures that include multiple sources
of variance and that filter out ‘fixed’ effects
such as demographic factors and experimental
conditions.

6. Evidence of Trait-Like Variance
Change in Total PVT lapses after two exposures 2-4 wks
apart of 36 h sleep deprivation.
Van Dongen HP, Kijkman M, Maislin G, Dinges D. Phenotypic aspect of
vigilance decrement during sleep deprivation. Physiologist 1999; 42:A-5.

7. Evidence of Trait-Like Variance
PVT Transformed Lapses Linear Slopes
Over 38 Hours (19 trials) of Sleep Deprivation
Monozygotic Twins
0.5
ICC = 56.0% (N=48 pairs)
Var(B) = 3.51*10E-3
PVT Transformed Lapses
0.4
Var(W) = 2.76*10E-3
Linear Slopes
0.3
0.2
0.1
0.0
-0.1
2
82
9
46
37
14
3
101
64
121
91
118
109
56
47
95
22
67
63
51
27
93
136
13
17
129
28
31
42
74
87
120
62
54
108
73
103
53
116
48
49
97
122
23
78
79
44
38
Twin Pair
Preliminary data from Heritability of Sleep
Homeostasis, Drs. Allan Pack and Samuel Kuna,
Division of Sleep Medicine.

8. Evidence of Trait-Like Variance
PVT Transformed Lapses Linear Slopes
Over 38 Hours (19 trials) of Sleep Deprivation
Dizygotic Twins
0.5
ICC = 24.5% (N=30 pairs)
Var(B) = 0.93*10E-3
PVT Transformed Lapses
0.4
Var(W) = 2.87*10E-3
Linear Slopes
0.3
0.2
0.1
0.0
-0.1
132
98
135
29
117
142
126
106
25
128
10
148
94
41
4
16
124
127
5
138
52
134
100
149
58
113
104
130
145
57
Twin Pair

9. ‘Test-bed’ Experiment1
 This sleep restriction experiment involved one adaptation day
and two baseline days with 8 h sleep opportunities (TIB
23:30–07:30), followed by randomization to 8 h, 6 h or 4 h
periods for nocturnal sleep (TIB ending at 07:30) for 14 days.
 13 Subjects randomized to 4 hrs TIB for 14 days
 13 Subjects randomized to 6 hrs TIB for 14 days
 9 Subjects randomized to 8 hrs TIB for 14 days
 Assessments every 2 hrs during wakefulness
1
Van Dongen HP, Maislin G, Mullington JM, and Dinges DF. The cumulative cost
of additional wakefulness: Dose-response effects on neurobehavioral functions and
sleep physiology from chronic sleep restriction and total sleep restriction.
Sleep 2003, 26(2):117-126.

10. Neurobehavioral Test Battery (NAB)
(1) Psychomotor vigilance task (PVT) (Dinges & Powell 1985)
(2) Probed recall memory (PRM) test that controls for reporting bias and evaluates free
recall/retention (Dinges et al 1993)
(3) Digit symbol substitution task (DSST) assesses cognitive throughput (speed/accuracy)
(4) Time estimation task (TET)
(5) Performance evaluation and effort rating scales (PEERS) to track self monitoring,
compensatory effort, and motivation (Dinges et al 1992)
(1) Karolinska Sleepiness Scale (KSS) (Akerstedt & Gillberg 1990)
(2) Stanford Sleepiness Sale (SSS) (Hoddes et al 1973)
(3) Visual analog scale (VAS) for mental and physical exhaustion
(4) Activation-Deactivation Checklist (AD-ACL)(Thayer 1986)
(5) Profile of Mood States (POMS) (McNair, Lorr, & Druppleman 1971)

11. Psychomotor vigilance task (PVT)
 Simple, high-signal-load reaction time (RT)
test designed to evaluate the ability to sustain
attention and respond in a timely manner to
salient signals.
 10 minute duration
 Yields six primary metrics on the capacity for
sustained attention and vigilance performance.

12. Psychomotor vigilance task (PVT)
 Frequency of lapses (RT>500 msec)
 Duration of the lapse domain (mean of 10% slowest
reciprocal RTs)
 Optimum response times (mean of 10% fastest RTs)
 False response frequency (errors),
 Frequency of non-responses (caused by spontaneous
sleep episodes)
 Fatigability function (slope computed from 1 minute
bins of mean 1/RTs).

13. Average Daily PVT Lapses/Trial
PVT Lapses Among 13 Subjects with PVT Lapses Among 13 Subjects with PVT Lapses Among 9 Subjects with
Time in Bed Restricted to 4 Hours Time in Bed Restricted to 6 Hours Time in Bed Restricted to 8 Hours
40 50 25
40 20
30
30 15
PVT Lapses
PVT Lapses
PVT Lapses
20
20 10
10
10 5
0
0 0
0 2 4 6 8 10 12 14 0 2 4 6 8 10 12 14 0 2 4 6 8 10 12 14
Day Day Day

14. Karolinska Sleepiness Scale (KSS)
Karolinska Sleepiness Scale (KSS)
Place the X next to the ONE statement that best describes your SLEEPINESS
during the PREVIOUS 5 MINUTES. You may also use the intermediate steps.
X
__ 1. very alert
__ 2.
__ 3. alert, normal level
__ 4.
__ 5. neither alert nor sleepy
__ 6.
__ 7. sleepy, but no effort to keep awake
__ 8.
__ 9. very sleepy, great effort to keep awake, fighting sleep
Use {UP/ DOWN} cursor keys to move X block, then press {ENTER}

15. Karolinska Sleepiness Scale (KSS)
Karolinska Sleepiness Score Among 13 Subjects Karolinska Sleepiness Score Among 13 Subjects Karolinska Sleepiness Score Among 9 Subjects
with Time in Bed Restricted to 4 Hours with Time in Bed Restricted to 6 Hours with Time in Bed Restricted to 8 Hours
10 10 10
8 8 8
6 6 6
KSS
KSS
KSS
4 4 4
2 2 2
0 0 0
0 2 4 6 8 10 12 14 0 2 4 6 8 10 12 14 0 2 4 6 8 10 12 14
Day Day Day

16. Observations
 For the subjective measure, end-of-study values
depend heavily on baseline values.
 The objective measure increased linearly throughout
the PSD protocol.
 The increase in the subjective measure was non-
linear with decelerating increases. Most of the
increase was very early.
 There was substantial variability among subjects in
both objective and subjective responses to PSD.

17. Substantial Variability in Responses to PSD
PVT Lapses Among 13 Subjects with
Time in Bed Restricted to 4 Hours
40
30
PVT Lapses
20
10
0
0 2 4 6 8 10 12 14
Day

18. Statistical Approaches
for Growth Curves
 Classical repeated measures analysis fails to recognize individual
response variance. It is a model for the mean response with no
recognition of true biological variability among subjects in the
magnitudes of their response.
 Mixed effects models for each individual observation include
random subject effects and can allow for a variety of covariance
structures that can reflect many different assumptions concerning
the nature of within subject correlations overtime (e.g. AR(1)).
Although theoretically appealing, concern has been raised about
the robustness of these models1. They also require sophisticated
statistical approaches that may not be immediately accessible to all
researchers.
1
Ahnn, Tonidandel, and Overall. Issues in use of Proc.Mixed to test the significance of
treatment effects in controlled clinical trials. J of Biopharm Stat 10(2):265-286, 2000

19. Standard Two Stage (STS) regression
 Using simple linear regression, a slope (and intercept) for each
subject are determined at the first stage. Second stage group
comparisons are made by comparing mean slopes.
 STS gives each subject’s first stage slope estimate equal
weight, which is not appropriate if the sample size or layout of
time values varies widely among subjects.
 STS disguises residual error, pooling it with between-subject
variance and biasing the latter upward. If residual variance is
small or the numerical values of variance components are not
themselves of interest, this is not a problem.

20. Standard Two Stage (STS) regression (cont.)
 STS does not account for the covariance between
slopes and intercepts.
 Parsimony: It is desirable to reduce the response
curve to a single number (eliminating the intercept).
 Slopes assume constant accumulations of deficit over
time. However, accumulation of deficits can be
decelerating or accelerating.

21. Mixed linear model determination of slopes
 The simultaneous determination of subject specific
slopes using maximum likelihood incorporates the
assumption that the slopes are normally distributed with
condition-specific mean values and a common variance.
 STS does not make this assumption, computing each
subject-specific slope independently from all other
subjects (robustness?).

22. Proposed Model: Two-Stage Non-Linear
Mixed Model Regression
∆(t)i(j) = Bi(j) · tθ + ε(t)i(j)
 ∆(t)i(j) = performance deficit for subject i in group j at
time t
 θ is a curvature parameter reflecting the nature of
non-linearity of growth in deficits
 Bi(j) are subject-specific “non-linear” slopes
 ε(t)i(j) are residual errors.

23. Reference
 Van Dongen HPA, Maislin G, Dinges DF.
Dealing with inter-individual differences in
the temporal dynamics of fatigue and
performance: Importance and techniques.
Aviat Space Environ Med 2004: 75:A147–
A154.

24. Proposed Model: Two-Stage Non-Linear
Mixed Model Regression
 The (non-linear) slopes are combinations of group
specific mean values and random effects reflecting
individual susceptibilities to the deprivation challenge.
 Bi(j) = β j + bi(j)
βj is the mean response in group j
bi(j) ~ Normal(0, σ2b).
σ2b is a subject specific variance contribution.
Bi(j) ~ Normal(βj,, σ2b ).

25. Three Methods of Estimating Bi(j)
 Two-stage Random Effects Regression1 with grid
search varying θ.
 REML2 (treating θ as fixed)
 MLE3 (estimating θ)
1
Feldman. Families of lines: random effects in linear regression, J Appl. Physiol.
64(4):1721-1732, 1988.
2
Diggle, Kiang, Zeger. Analysis of Longitudinal Data, Oxford: Clarendon Press, 1996,
pages 64-68.
3
Vonesh: Nonlinear Models for the Analysis of Longitudinal Data. Stat. in Med, 11,
1929 – 1954, 1992.

26. Two-stage Random Effects Regression
with Grid search varying θ
 Simple linear regression for each subject
varying θ from 0.1 to 2.0.
 The θ that minimizes the average MSE is
selected.

27. Two-stage Random Effects Regression
with Grid search varying θ
Fig. 1 Grid Search Over Average MSE
from First Stage Linear Regressions
on Delta PVT Lapses Values
24
22
Theta = 0.78
20
Mean MSE
18
16
14
12
10
0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 2.0
Curvature (Theta)

28. REML Mixed Linear Model (fixed θ)
 The 2-stage approach disguises residual error, pooling
it with between-subject variance and biasing the latter
upward (compare SD’s in Table 1 and Table 2).
 Conditional on the value of the optimal θ obtained
from the grid search, the model is no longer non-linear.
 When θ is assumed known, a mixed linear model can
be used to simultaneously derive subject specific
slopes (e.g., SAS Proc Mixed).

29. ML Mixed Non-Linear Model
(simultaneous estimation of θ)
 Has greatest theoretical appeal.
 Requires specialized software
(e.g., SAS Proc NLMIXED).
 Model sometimes does not converge.
 More precise estimate of θ (Table 3).

30. Examples of Second Stage Analysis
Fig. 2 Delta PVT Lapses
REML (fixed theta) Non-linear Slopes
by Study Group (Theta=0.78)
6
F2,30=3.67, p=0.037
5
Non-linear Slope
4
3
2
1
0
-1
4 hr 6 hr 8 hr
Group

31. Examples of Second Stage Analysis
Table 1. Two-stage Non-linear Slopes (θ=0.7753)
N Mean SD Min Max
4 hr 13 1.9269 1.3493 0.0638 3.8784
6 hr 13 1.2897 1.6999 -0.5383 5.5608
8 hr 9 0.3345 0.6851 -0.3228 2.0517

32. Examples of Second Stage Analysis
Table 2. REML Mixed Model Non-linear Slopes (θ=0.7753)
N Mean SD Min Max
4 hr 13 1.9269 1.3245 0.0981 3.8425
6 hr 13 1.2897 1.6686 -0.5046 5.4822
8 hr 9 0.3345 0.6721 -0.3107 2.0201

33. Examples of Second Stage Analysis
Table 3. ML Non Linear Mixed Model Results
Standard
Label Estimate Error DF t Value Pr > |t|
theta 0.7753 0.0397 34 19.51 <.0001
4hr Slope 1.9267 0.4028 34 4.78 <.0001
6hr Slope 1.2896 0.3820 34 3.38 0.0019
8hr Slope 0.3352 0.4390 34 0.76 0.4504
BTW Subj SD 1.3010 0.1985 34 6.55 <.0001
Resid SD 3.2918 0.1096 34 30.03 <.0001
Total Var 12.5288 0.8848 34 14.16 <.0001
Total SD 3.5396 0.1250 34 28.32 <.0001

34. Examples of Second Stage Analysis
Parameter Estimates
Standard
Parameter Estimate Error DF t Value Pr > |t| Alpha Lower
beta0 0.3352 0.4390 34 0.76 0.4504 0.05 -0.5569
s2beta 1.6927 0.5166 34 3.28 0.0024 0.05 0.6428
theta 0.7753 0.03974 34 19.51 <.0001 0.05 0.6946
s2e 10.8361 0.7216 34 15.02 <.0001 0.05 9.3697
bcond4 1.5915 0.5876 34 2.71 0.0105 0.05 0.3974
bcond6 0.9544 0.5762 34 1.66 0.1069 0.05 -0.2167

35. 2-Stage Regression Non-linear Slopes
PVT Lapses
Delta PVT Lapses
Two-Stage Non-linear Slopes
by Study Group (Theta=0.7753)
6
5
Non-linear Slope
4
3
2
1
0
-1
4 hour 6 hour 8 hour
Sleep Condition

36. REML: PVT Lapses
Assuming θ Known
Delta PVT Lapses
REML (fixed theta) Non-linear Slopes
by Study Group (Theta=0.7753)
6
5
Non-linear Slope
4
3
2
1
0
-1
4 hour 6 hour 8 hour
Sleep Condition

37. Two-stage vs. REML Mixed Model
Delta PVT Lapses
Attenuation of Extremes Produce by REML
9
8 Attenuation Slope=0.9999
REML Non-linear Slope
7
6
5
4
3
2
1
0
-1
-2
-3
-3 -2 -1 0 1 2 3 4 5 6 7 8 9
Two-Stage Non-linear Slope

38. 2-Stage Regression Non-linear Slopes
PVT Lapses
Delta PVT Lapses
Two-Stage Non-linear Slopes
by Study Group (Theta=1.1)
10
8
Non-linear Slope
6
4
2
0
-2
-4
Active Placebo
Group

39. REML: PVT Lapses
Assuming θ Known
Delta PVT Lapses
REML (fixed theta) Non-linear Slopes
by Study Group (Theta=1.1)
10
8
Non-linear Slope
6
4
2
0
-2
-4
Active Placebo
Group

40. Two-stage vs. REML Mixed Model
Delta PVT Lapses
Attenuation of Extremes Produce by REML
9
8 Attenuation Slope=0.925
REML Non-linear Slope
7
6
5
4
3
2
1
0
-1
-2
-3
-3 -2 -1 0 1 2 3 4 5 6 7 8 9
Two-Stage Non-linear Slope

41. Analysis for KSSQ (theta=0.1607)
N
COND Obs Variable N Mean Std Dev Minimum Maximum
----------------------------------------------------------------------
4 13 SLOPE 13 1.3488 0.8470 0.2265 3.1963
SLOPE_MIXED 13 1.3488 0.7402 0.3679 2.9635
6 13 SLOPE 13 1.0061 0.6925 -0.0035 2.3645
SLOPE_MIXED 13 1.0061 0.6052 0.1237 2.1934
8 9 SLOPE 9 0.1297 0.5857 -0.6041 1.1054
SLOPE_MIXED 9 0.1315 0.5112 -0.5114 0.9827
----------------------------------------------------------------------
Note that the mean 2-stage slope and the mean
mixed model slope are not identical for KSSQ
in the 8 hour condition because there was a
missing value. The mixed model slopes
correctly adjust for the reduced precision
caused by the single missing value.

42. Analysis for KSSQ (theta=0.1607)
Parameter Estimates
Standard
Parameter Estimate Error DF t Value Pr > |t| Alpha Lower
beta0 0.1304 0.2335 34 0.56 0.5803 0.05 -0.3442
s2beta 0.4662 0.1292 34 3.61 0.0010 0.05 0.2037
theta 0.1607 0.03084 34 5.21 <.0001 0.05 0.09800
s2e 0.5868 0.03907 34 15.02 <.0001 0.05 0.5074
bcond4 1.2185 0.3129 34 3.89 0.0004 0.05 0.5825
bcond6 0.8758 0.3082 34 2.84 0.0075 0.05 0.2494
Contrasts
Num Den
Label DF DF F Value Pr > F
Overall Slope Diff 2 34 7.76 0.0017
4 vs 6 Slope 1 34 1.55 0.2217
4 vs 8 Slope 1 34 15.16 0.0004
6 vs 8 Slope 1 34 8.07 0.0075

43. Analysis for KSSQ (theta=0.1607)
Additional Estimates
Standard
Label Estimate Error DF t Value Pr > |t| Alpha Lower
4hr Slope 1.3488 0.2110 34 6.39 <.0001 0.05 0.9201
6hr Slope 1.0062 0.2032 34 4.95 <.0001 0.05 0.5933
8hr Slope 0.1304 0.2335 34 0.56 0.5803 0.05 -0.3442
BTW Subj SD 0.6828 0.09460 34 7.22 <.0001 0.05 0.4905
Resid SD 0.7660 0.02550 34 30.03 <.0001 0.05 0.7142
Total Var 1.0530 0.1346 34 7.83 <.0001 0.05 0.7795
Total SD 1.0261 0.06557 34 15.65 <.0001 0.05 0.8929
Note that estimated slopes using ML are identical to
REML because the ML theta was used.

44. Results from Twin Study
Pooled Mean Change in
Transformed PVT Lapses
7
MZ
6
Change in Transformed
PVT Lapses Per Trial DZ
5
4
3
2
1
0
-1
4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38
Hours Post 7:30am Awakening

45. Results from Twin Study
E(θ it) =
β i0 + β i1*t + ai*cos(2*Π*t/24) + bi*sin(2*Π*t/24)

46. Results from Twin Study
Predicted Change in PVT Lapses
Change in PVT Lapses Per Trial Linear plus Single Harmonic Model
25 Tw 1/A
Tw 1/B
Tw 2/A
20 Tw 2/B
Tw 3/A
Tw 3/B
15 Tw 4/A
Tw 4/B
Tw 5/A
10
Tw 5/B
Tw 9/A
5 Tw 9/B
Tw 10/A
Tw 10/B
0 Tw 13/A
Tw 13/B
Tw 14/A
-5 Tw 14/B
4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 Tw 16/A
Tw 16/B
Hours Post 7:30am Awakening

47. Results from Twin Study
Heritability Indices Classical Approach
PVT Linear Slopes
Monozygotic Twins Dizygotic Twins
σ 2B σ 2W σ 2T ICC σ 2B σ 2W σ 2T ICC h2
Transformed 0.63
Lapses 3.51 2.76 6.27 0.560 0.93 2.87 3.80 0.245
1

48. An Application in Another Area
 Berkowitz RI, Stallings VA, Maislin G, Stunkard AJ.
Growth of children at high risk for obesity during the
first six years: Implications for prevention. American
Journal of Clinical Nutrition. Am J Clinical Nutrition
2005;81:140–6.
 Body size and composition of high and low risk
groups were measured repeatedly from 3 mo. to 6 yrs
of age at CHOP. Subjects included 33 children at
high risk for and 37 children at lower risk for obesity
on the basis of mothers’ overweight1
1
high risk mean (SD) BMI = 30.2 (4.2), low risk mothers’ BMI = 19.5 (1.1).

49. An Application in Another Area
 At year 2, there were no differences between high
and low risk groups in any measure of body size
and composition1
 (Energy intake and sucking behaviors at Month 3
were predictive of 2 year weight in both groups.)
1
Stunkard AJ, Berkowitz RI, Schoeller D, Maislin G, Stallings VA. Predictors of body size in the
first 2 years of life: a high-risk study of human obesity. International Journal of Obesity 2004
1-11.

50. Weight Over Time
Weight Over Time From Month 24 to Month 72
From Month 24 to Month 72 Low Risk Group
High Risk Group
50
50
Low Risk
High Risk 40
40
Weight (kg)
30
Weight (kg)
30
20
20
10
10
0
0 24 30 36 42 48 54 60 66 72
24 30 36 42 48 54 60 66 72 Month
Month
Average Mean Squared Error
from First Stage Linear Regressions Change in Weight from Month 24 to Month 72
on Delta Weight from Month 24 to Month 72 REML (fixed theta) Non-linear Slopes
by Risk Group (Theta=2.4)
12 0.07
Mean (SD) Non-Linear Slopes
10 0.06 High Risk 0.024 (0.011)
Theta = 2.4 Low Risk 0.018 (0.004)
Non-linear Slope
Unequal Variance t-test p=0.010
0.05
Mean MSE
8
0.04
6
0.03
4 0.02
0.01
2
0.00
0 High Risk Low Risk
0.2 0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8 2.0 2.2 2.4 2.6 2.8 3.0 3.2 3.4 Group
Curvature (Theta)

51. Parsimony of Interpretations
Change in Weight from Month 24 to Month 72
REML (fixed theta) Non-linear Slopes
by Group (Theta=2.4)
0.07
0.06
Non-linear Slope
0.05
0.04
0.03
0.02
0.01
0.00
High GT 85th High LE 85th Low
Group

52. Generally monotonic but varying in
direction:
 It is possible that trajectories are generally
monotonic but vary in direction (i.e., there are
subgroups of individuals with generally
increasing values and others with generally
decreasing values over time).
 In this case, θ can be set to 1 with slope
estimated individually using two-stage random
effects regression or simultaneously by Proc
Mixed.

53. Generally non-monotonic changes:
 If trajectories are non-monotonic (e.g. quadratic), mixed model analyses of
longitudinal changes can be performed that incorporate multiple time
variables such as linear plus quadratic terms or appropriately constructed
sets of time indicator variables.
 Correlations among observations within subject can be accounted for by
using appropriately constructed covariance matrices1. A particular
covariance structure is the ‘random intercept plus AR(1)’ structure. This
structure induces within subject correlations by assuming both systematic
variance in overall levels between subjects plus a component that
diminishes over time.
1
Littell RC, Pendergast J, Natarajan R. Tutorial in biostatistics: Modeling covariance
structure in the analysis of repeated measures data. Statistics in Medicine. 19:1793-1819,
2000.

54. General Linear Mixed Model:
 Verbeke G and Molenberghs G (2000). Linear Mixed
Models for Longitudinal Data. Springer Series in
Statistics. New-York: Springer.
 Yi = Xiβ + Zibi + εi bi ~ N(0,D), εi ~ N(0, ∑i)
 b1, . . . , bN, εi , . . . , εN independent
 Terminology
 Fixed effects: β
 Random effects: bi
 Variance components: Elements in D and ∑i

55. General Linear Mixed Model:
 Hierarchical model can be rewritten as:
Yi|bi ~ N(Xiβ + Zibi, ∑i); bi ~ N(0,D)
 Marginal model can be rewritten as:
Yi ~ N(Xiβ, ZibiZ'i +∑i)
 The hierarchical model is most naturally interpreted
through a Bayesian perspective
 Only the hierarchical model explicitly assumes inter-
individual variability

56. General Linear Mixed Model:
 Prior distribution: f(bi) = N(0,D)
 Likelihood function: f(yi|bi) = N(Xiβ + Zibi, ∑i)
 Posterior distribution:
f(bi | Yi = yi) α f(yi|bi) * f(bi)
 Posterior mean: ∫ bi f(bi | yi) dbi is the Empirical
Bayes estimate of bi

57. Conclusions
 The STS, REML, and ML approaches have advantages and
disadvantages.
 “The great advantage of the STS, aside from conceptual and
computational simplicity, is the availability of valid small-
sample statistics. STS can thus be relied upon, whereas WLS
and REML cannot, to produce accurate P values in the cases
of very few subjects, so long as the assumptions of the small-
sample model (e.g., normality) are met1”
 The ML approach requires starting values (guesses) for every
parameter and sometimes the ML optimization does not
converge.
1
Feldman HA. Families of lines: random effects in linear regression analysis, J.
Appl. Physiol. 64(4):1721-1732, 1988.

58. Conclusions
 The “grid search plus STS” method provides good
solutions that in most cases are very similar to the
optimal ML solutions, facilitate analysis of inter-
individual variability in responses to sleep
deprivation, and is easy to implement.
 The model: ∆(t)i(j) = Bi(j) · tθ + ε(t)i(j) can be
generally recommended for sets of responses that are
generally monotonic.
 Other methods are needed for non-monotonic
trajectories. The cost of non-monotonicity is greater
analytical complexity.

59. Conclusions
 The Linear Mixed Model provides a
comprehensive platform for evaluation and
estimation of inter-individual variability
including the evaluation of prior and posterior
distributions of subject specific parameters. It
may be possible to update subject specific
parameters reflecting individual performance,
and then sum over these individual
performance estimates to obtain a summary
prediction of unit performance.