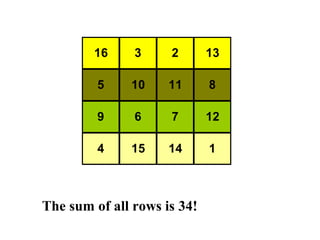
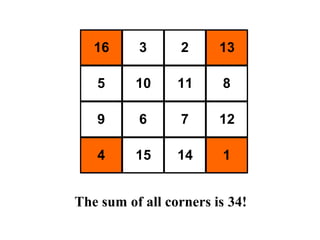
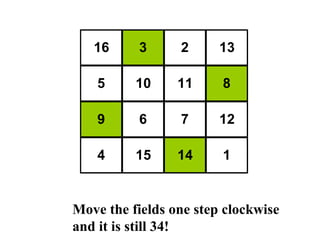
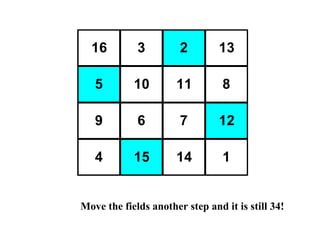
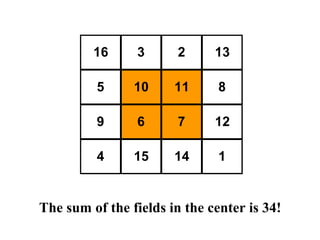
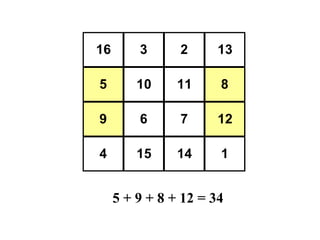
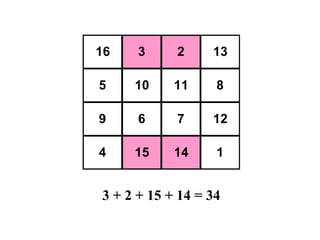
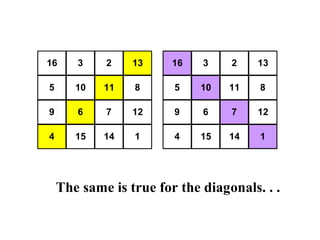
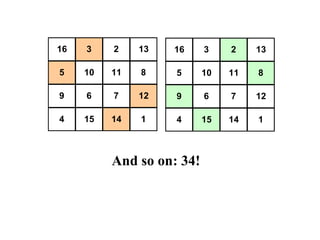
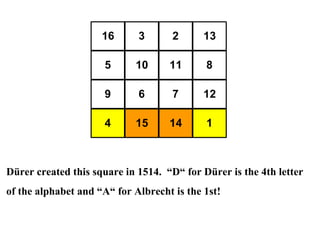
The document summarizes Albrecht Dürer's magic square from 1514. It notes that the magic of the square is that the sum of any row, column, diagonal or selection of center squares is always 34. Dürer was proud of this creation as the numbers 4 and 1 represent his initials.

1. Albrecht Dürer
And his magic square

2. On the wall to the
right hangs the
magic square Dürer
created.

3. It looks like this.
16 3 2 13 And what is the magic?
It is the number 34!
5 10 11 8
9 6 7 12
This number is the sum of the
various fields within the magic
4 15 14 1 square.

4. 16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
The sum of all rows is 34!

5. 16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
The sum of all columns is 34!

6. 16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
The sum of all corners is 34!

7. 16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
Move the fields one step clockwise
and it is still 34!

8. 16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
Move the fields another step and it is still 34!

9. 16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
The sum of the fields in the center is 34!

10. 16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
5 + 9 + 8 + 12 = 34

11. 16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
3 + 2 + 15 + 14 = 34

12. 16 3 2 13 16 3 2 13
5 10 11 8 5 10 11 8
9 6 7 12 9 6 7 12
4 15 14 1 4 15 14 1
The same is true for the diagonals. . .

13. 16 3 2 13 16 3 2 13
5 10 11 8 5 10 11 8
9 6 7 12 9 6 7 12
4 15 14 1 4 15 14 1
And so on: 34!

14. 16 3 2 13
5 10 11 8
9 6 7 12
4 15 14 1
Dürer created this square in 1514. “D“ for Dürer is the 4th letter
of the alphabet and “A“ for Albrecht is the 1st!

15. Genius!
. . . He was very
proud for creating
this magic square –
and he should be!

16. Shared by a member of NidoKidoS Group
Subscribe by email | Visit website | Join our Forum
*Nidokidos is just sharing this file.
all rights are reserved by the respective authors of this presentation.