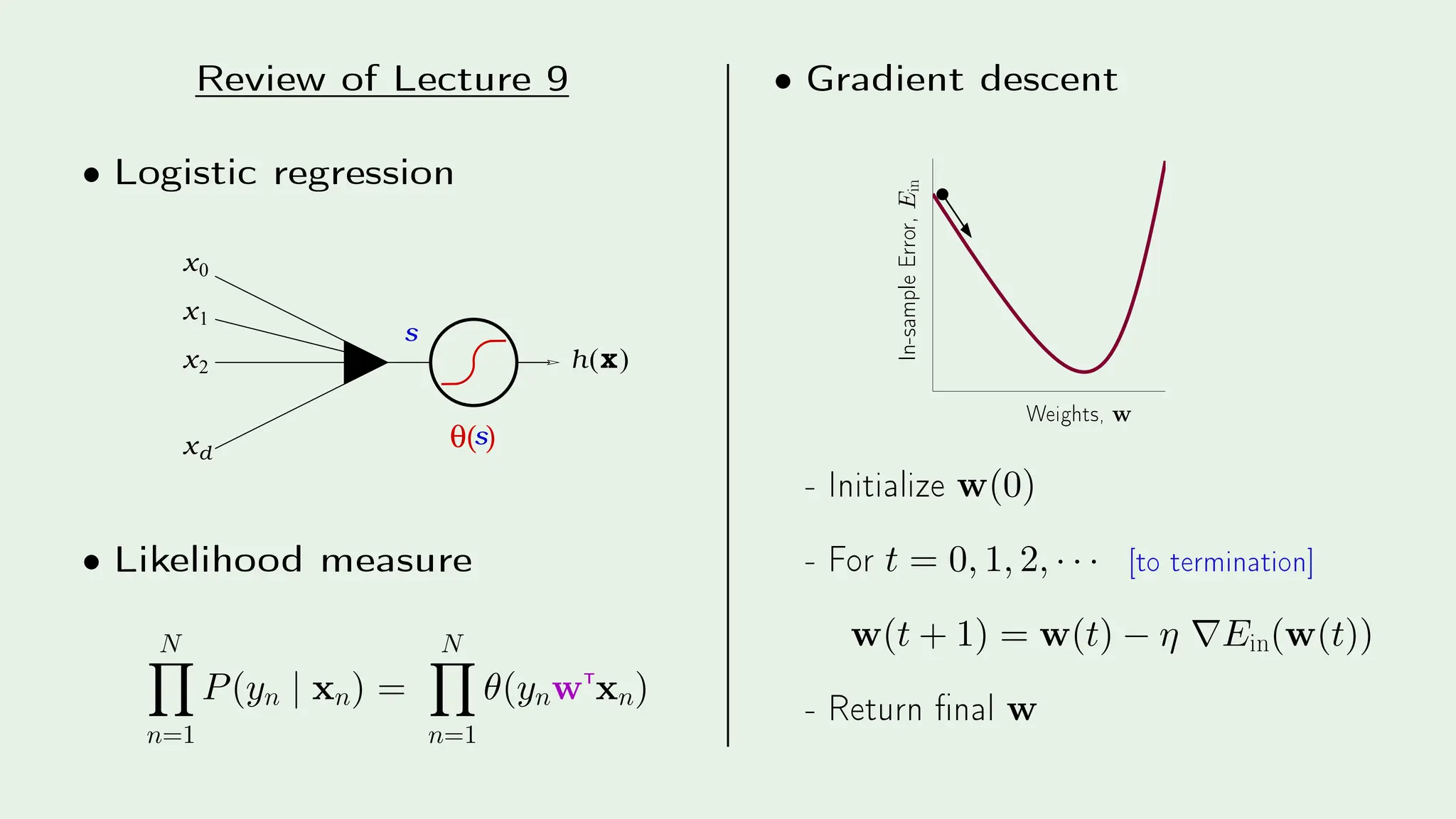
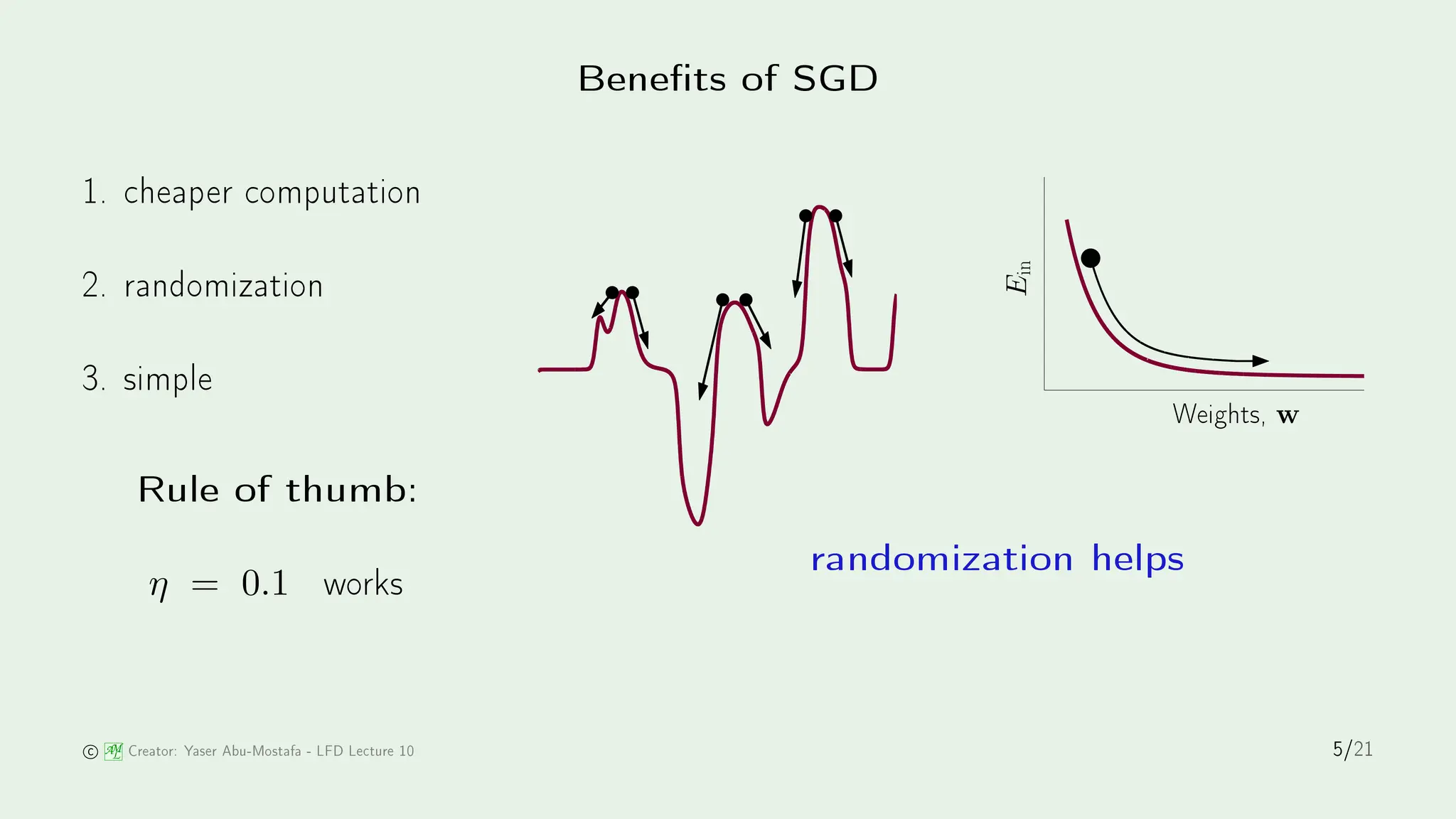
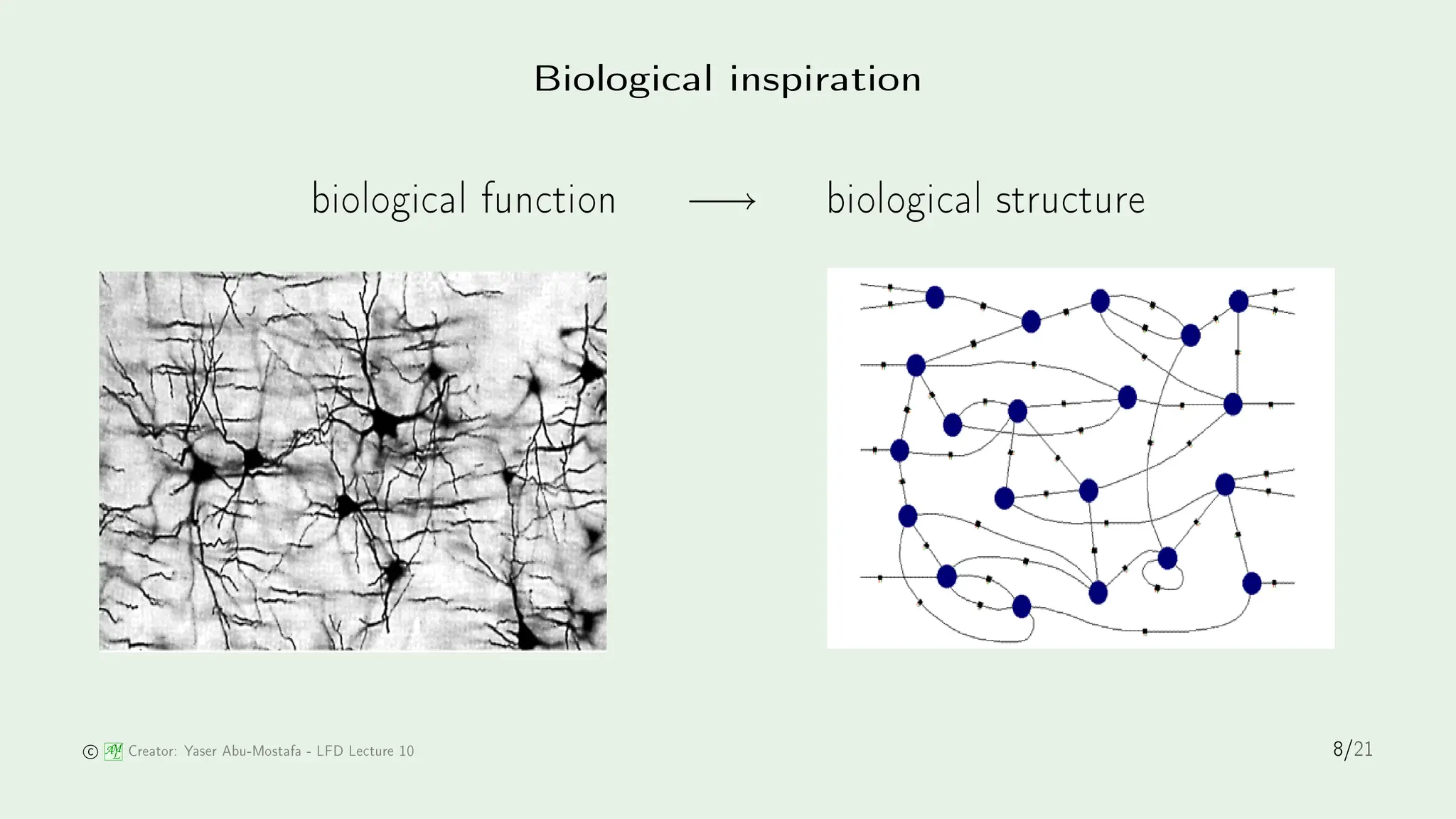
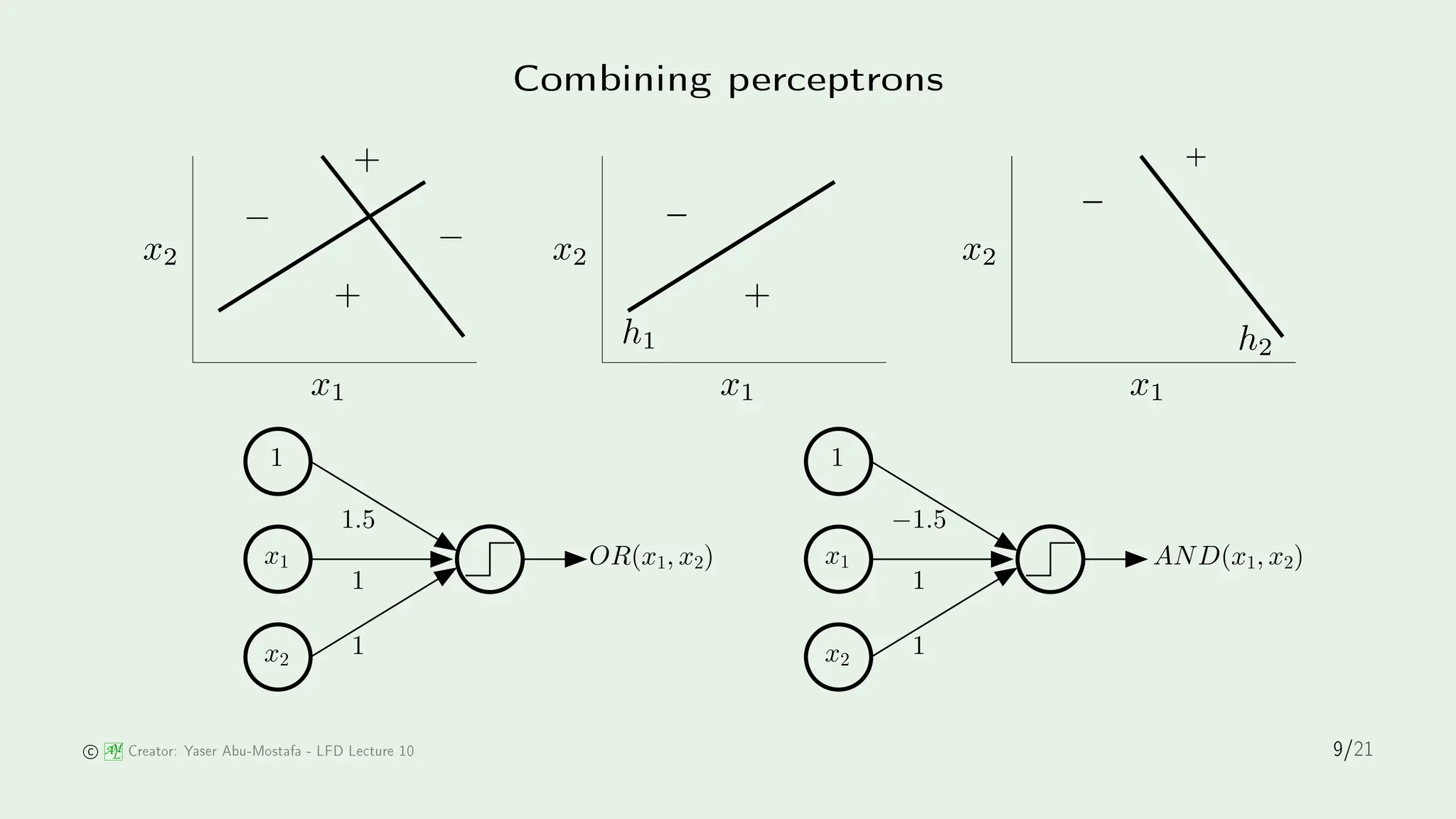
The document discusses stochastic gradient descent (SGD) and its application in logistic regression and neural networks, outlining the principles of how SGD minimizes error through iterative weight updates. It further details the backpropagation algorithm as a method for training multilayer perceptrons through the calculation of gradients. The influence of biological inspiration on neural network architecture is also addressed, emphasizing the complexity and power of neural models.

1. Review of Le ture 9
• Logisti regression
s
x
x
x
x0
1
2
d
h x
( )
s
θ( )
• Likelihood measure
N
Y
n=1
P(yn | xn) =
N
Y
n=1
θ(ynwT
xn)
• Gradient des ent
Weights, w
In-sample
Error,
E
in
-10
-8
-6
-4
-2
0
2
10
15
20
25
- Initialize w(0)
- For t = 0, 1, 2, · · · [to termination℄
w(t + 1) = w(t) − η ∇Ein(w(t))
- Return nal w

2. Learning From Data
Yaser S. Abu-Mostafa
California Institute of Te hnology
Le ture 10: Neural Networks
Sponsored by Calte h's Provost O e, EAS Division, and IST • Thursday, May 3, 2012

3. Outline
• Sto hasti gradient des ent
• Neural network model
• Ba kpropagation algorithm
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 2/21

4. Sto hasti gradient des ent
GD minimizes: Ein(w) =
1
N
N
X
n=1
e h(xn), yn
| {z }
ln(1+e−ynwTxn) ←− in logisti regression
by iterative steps along −∇Ein:
∆w = − η ∇Ein(w)
∇Ein is based on all examples (xn, yn)
bat h GD
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 3/21

5. The sto hasti aspe t
Pi k one (xn, yn) at a time. Apply GD to e h(xn), yn
Average dire tion: En
−∇e h(xn), yn
=
1
N
N
X
n=1
−∇e h(xn), yn
= −∇ Ein
randomized version of GD
sto hasti gradient des ent (SGD)
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 4/21

6. Benets of SGD
Weights, w
E
in
1
2
3
4
5
6
0
0.05
0.1
0.15
randomization helps
1. heaper omputation
2. randomization
3. simple
Rule of thumb:
η = 0.1 works
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 5/21

7. SGD in a tion
rating
m o v i e
top
i
j
rij
u u u u
i1 i2 i3 iK
j1
v v v jK
v
j2 j3
u s e r
bottom
Remember movie ratings?
eij = rij −
K
X
k=1
uikvjk
!2
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 6/21

8. Outline
• Sto hasti gradient des ent
• Neural network model
• Ba kpropagation algorithm
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 7/21

9. Biologi al inspiration
biologi al fun tion −→ biologi al stru ture
1
2
1
2
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 8/21

10. Combining per eptrons
−
−
+
x1
x2
+
−
h1
x1
x2
+
+
−
h2
x1
x2
OR(x1, x2)
1
x1
x2
1
1
1.5 −1.5
1
x1
x2
AND(x1, x2)
1
1
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 9/21

11. Creating layers
1
1
h1h̄2
h̄1h2
f
1.5
1
1
f
1
1.5
1
1
1
h1
h2
−1
−1
−1.5
−1.5
1
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 10/21

12. The multilayer per eptron
w1 • x
f
1
1.5
1
1
1 1
−1
−1
−1.5
−1.5
1
1
x1
x2
w2 • x
3 layers feedforward
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 11/21

13. A powerful model
−
−
−
+
+
+
−
+
− −
−
−
+
+
+
+
− −
−
+
+
+
−
+
Target 8 per eptrons 16 per eptrons
2 red ags for generalization and optimization
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 12/21

14. The neural network
θ
x2
xd
s
θ(s)
h(x)
1
1 1
x1
input x hidden layers 1 ≤ l L output layer l = L
θ
θ
θ θ
θ
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 13/21

15. How the network operates
linear
tanh
hard threshold
+1
−1
-4
-2
0
2
4
-1
-0.5
0
0.5
1
θ(s) = tanh(s) =
es
− e−s
es + e−s
w
(l)
ij







1 ≤ l ≤ L layers
0 ≤ i ≤ d(l−1)
inputs
1 ≤ j ≤ d(l)
outputs
x
(l)
j = θ(s
(l)
j ) = θ


d(l−1)
X
i=0
w
(l)
ij x
(l−1)
i


Apply x to x
(0)
1 · · · x
(0)
d(0) → → x
(L)
1 = h(x)
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 14/21

16. Outline
• Sto hasti gradient des ent
• Neural network model
• Ba kpropagation algorithm
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 15/21

17. Applying SGD
All the weights w = {w
(l)
ij } determine h(x)
Error on example (xn, yn) is
e h(xn), yn
= e(w)
To implement SGD, we need the gradient
∇e(w):
∂ e(w)
∂ w
(l)
ij
for all i, j, l
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 16/21

18. Computing
∂ e(w)
∂ w
(l)
ij
x
w
s
x
i
ij
j
j
(l)
(l)
(l)
(l−1)
top
bottom
θ
We an evaluate
∂ e(w)
∂ w
(l)
ij
one by one: analyti ally or numeri ally
A tri k for e ient omputation:
∂ e(w)
∂ w
(l)
ij
=
∂ e(w)
∂ s
(l)
j
×
∂ s
(l)
j
∂ w
(l)
ij
We have
∂ s
(l)
j
∂ w
(l)
ij
= x
(l−1)
i We only need:
∂ e(w)
∂ s
(l)
j
= δ
(l)
j
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 17/21

19. δ for the nal layer
δ
(l)
j =
∂ e(w)
∂ s
(l)
j
For the nal layer l = L and j = 1:
δ
(L)
1 =
∂ e(w)
∂ s
(L)
1
e(w) = ( x
(L)
1 − yn)2
x
(L)
1 = θ(s
(L)
1 )
θ′
(s) = 1 − θ2
(s) for the tanh
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 18/21

20. Ba k propagation of δ
x i
(l−1)
x i
(l−1) 2
wij
j
xj
(l)
(l)
(l)
δ
δi
(l−1)
1−( )
top
bottom
δ
(l−1)
i =
∂ e(w)
∂ s
(l−1)
i
=
d(l)
X
j=1
∂ e(w)
∂ s
(l)
j
×
∂ s
(l)
j
∂ x
(l−1)
i
×
∂ x
(l−1)
i
∂ s
(l−1)
i
=
d(l)
X
j=1
δ
(l)
j × w
(l)
ij × θ′
(s
(l−1)
i )
δ
(l−1)
i = (1 − (x
(l−1)
i )2
)
d(l)
X
j=1
w
(l)
ij δ
(l)
j
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 19/21

21. Ba kpropagation algorithm
wij
(l)
δj
(l)
x
(l−1)
i
top
bottom
1: Initialize all weights w
(l)
ij at random
2: for t = 0, 1, 2, . . . do
3: Pi k n ∈ {1, 2, · · · , N}
4: Forward: Compute all x
(l)
j
5: Ba kward: Compute all δ
(l)
j
6: Update the weights: w
(l)
ij ← w
(l)
ij − η x
(l−1)
i δ
(l)
j
7: Iterate to the next step until it is time to stop
8: Return the nal weights w
(l)
ij
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 20/21

22. Final remark: hidden layers
θ
x2
xd
s
θ(s)
h(x)
1
1 1
x1
θ
θ
θ θ
θ
learned nonlinear transform
interpretation?
AM
L Creator: Yaser Abu-Mostafa - LFD Le ture 10 21/21