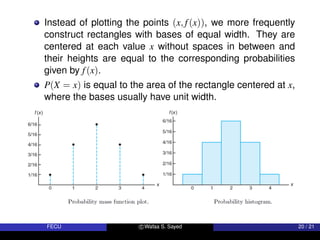
The document discusses random variables and probability distributions, focusing on their definitions and types, such as discrete and continuous random variables. It provides illustrative examples, defining how random variables can be applied in statistical inference regarding populations and characteristics, including practical scenarios like sampling plans and defect probabilities. Key definitions include the nature of discrete and continuous sample spaces, as well as the formulation of probability mass functions.