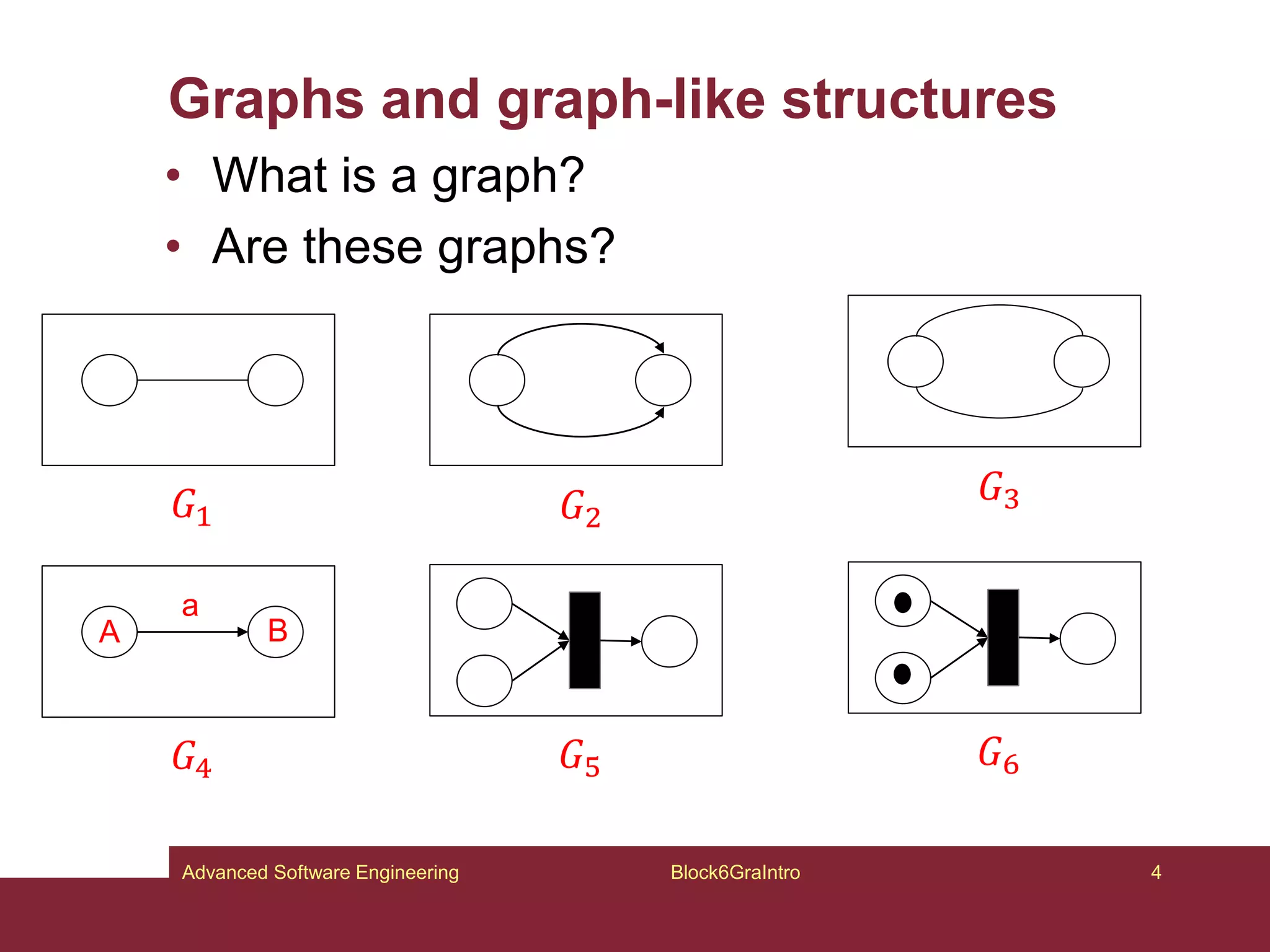
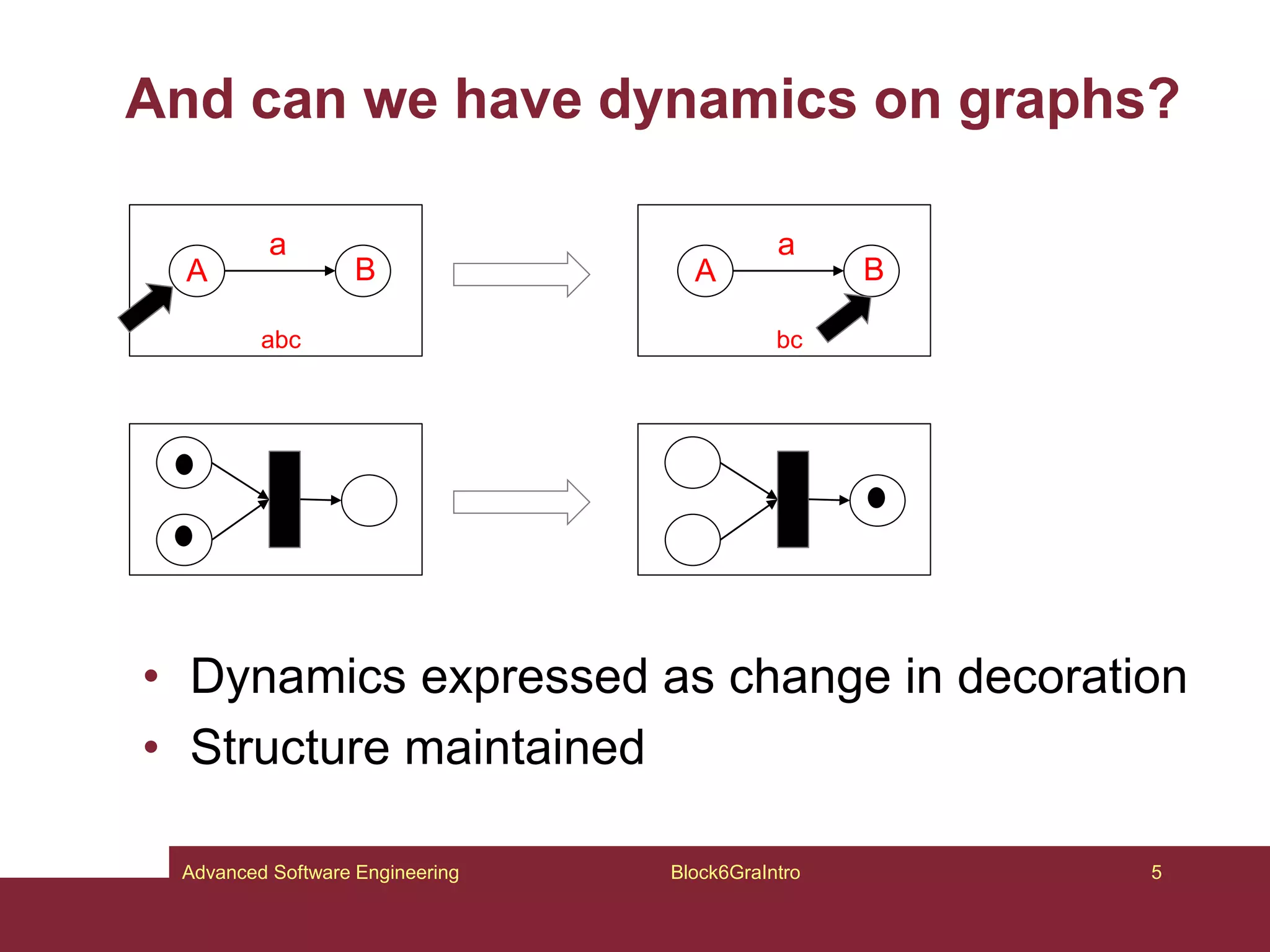
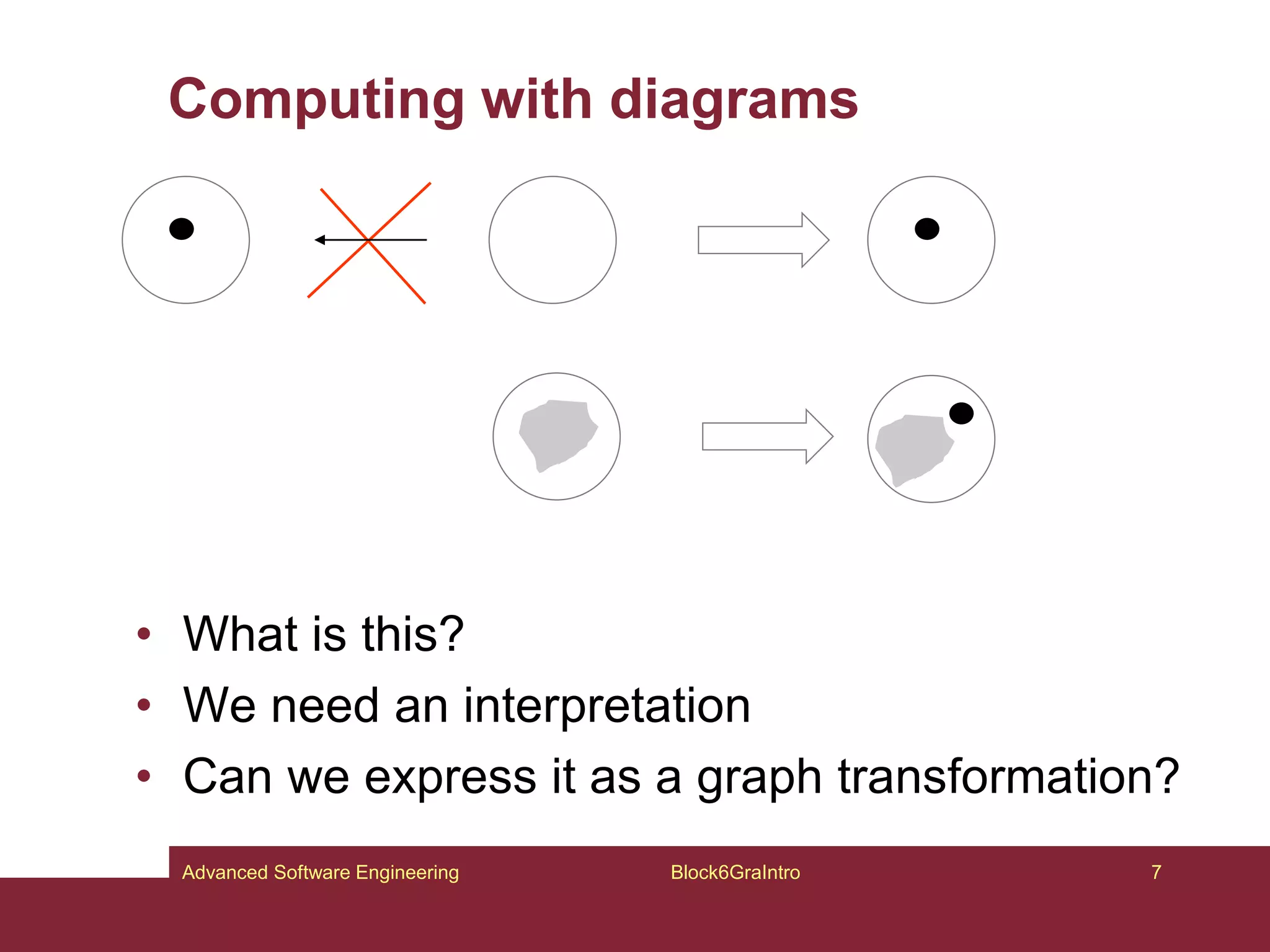
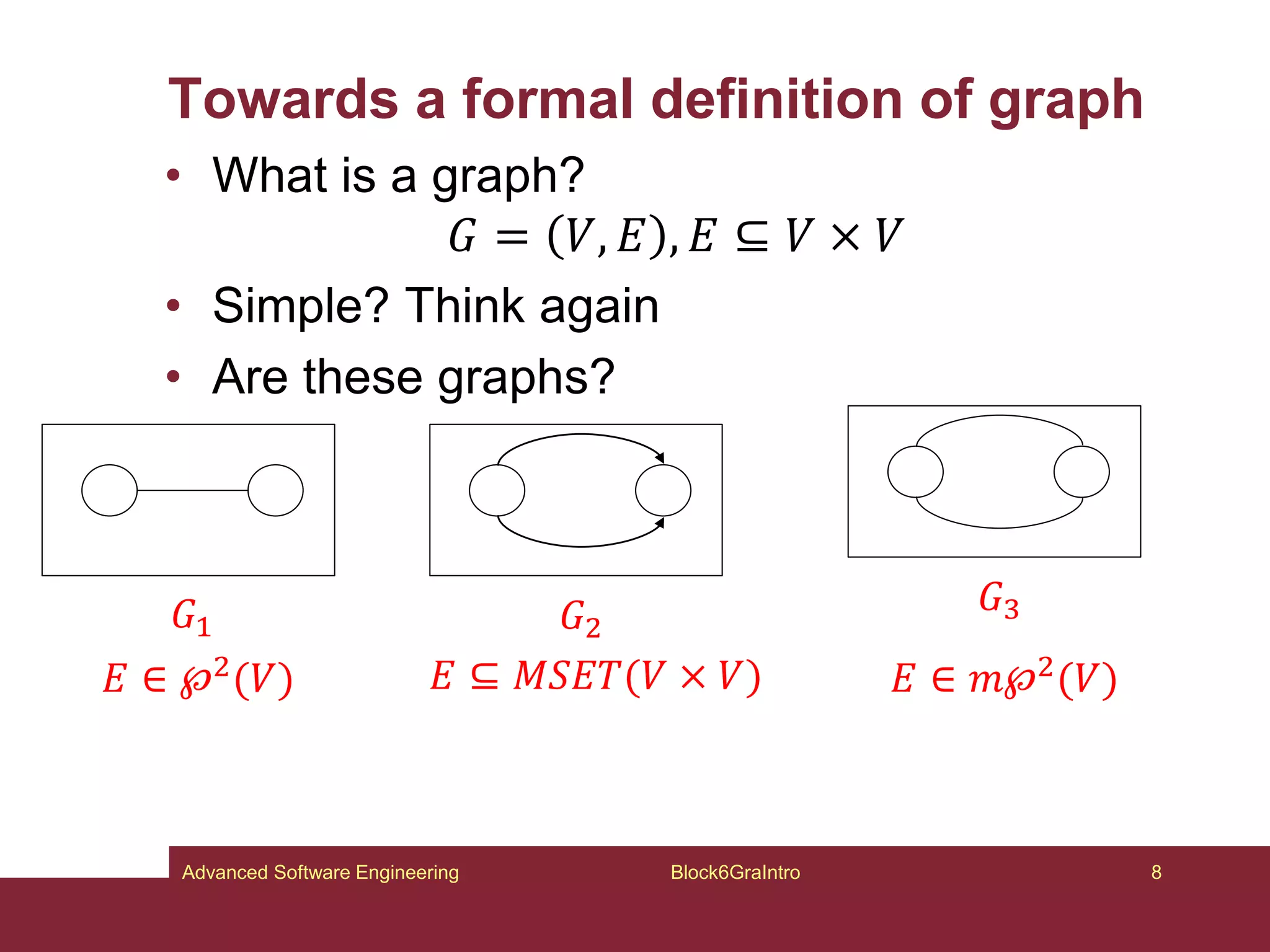
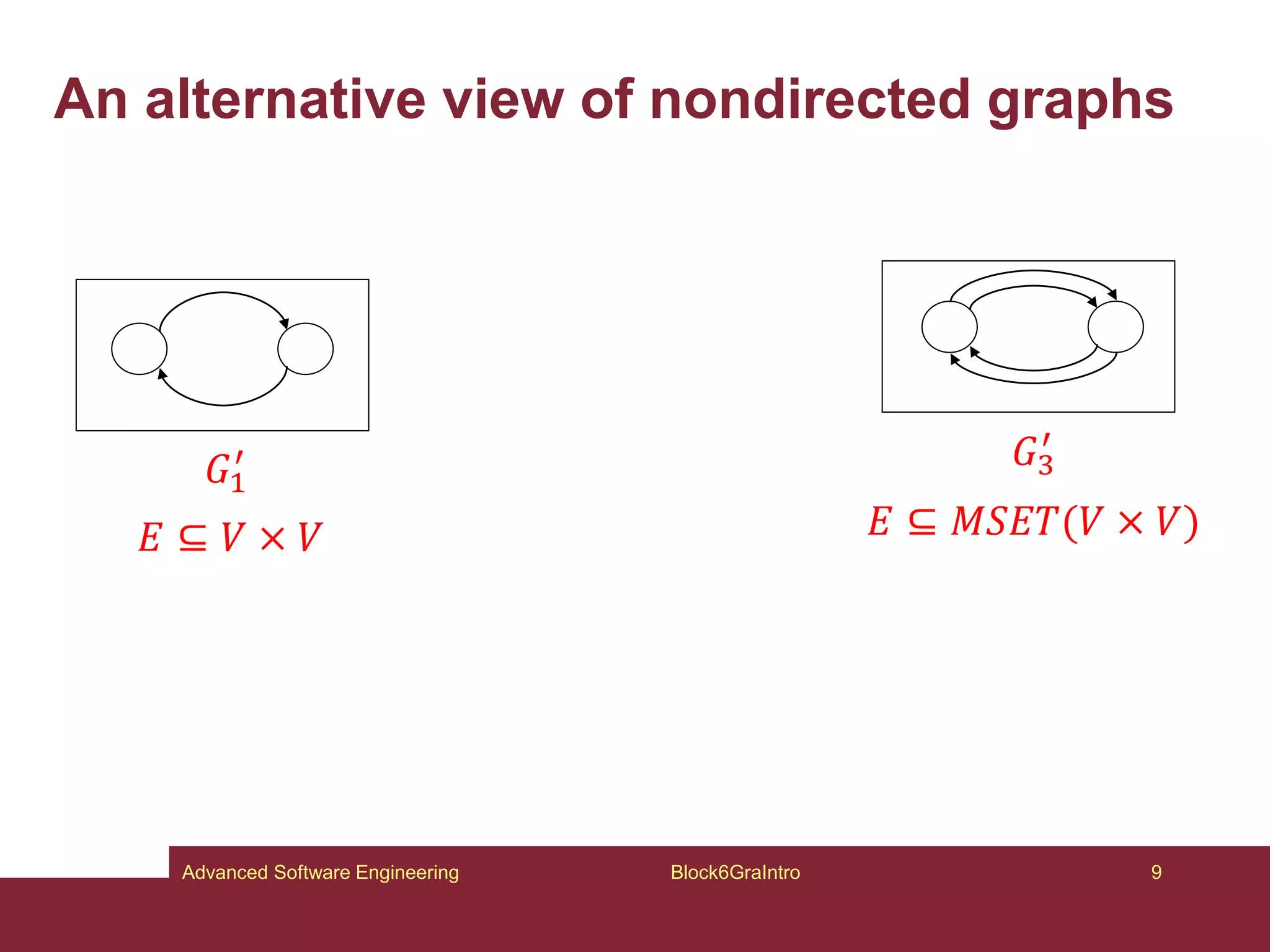
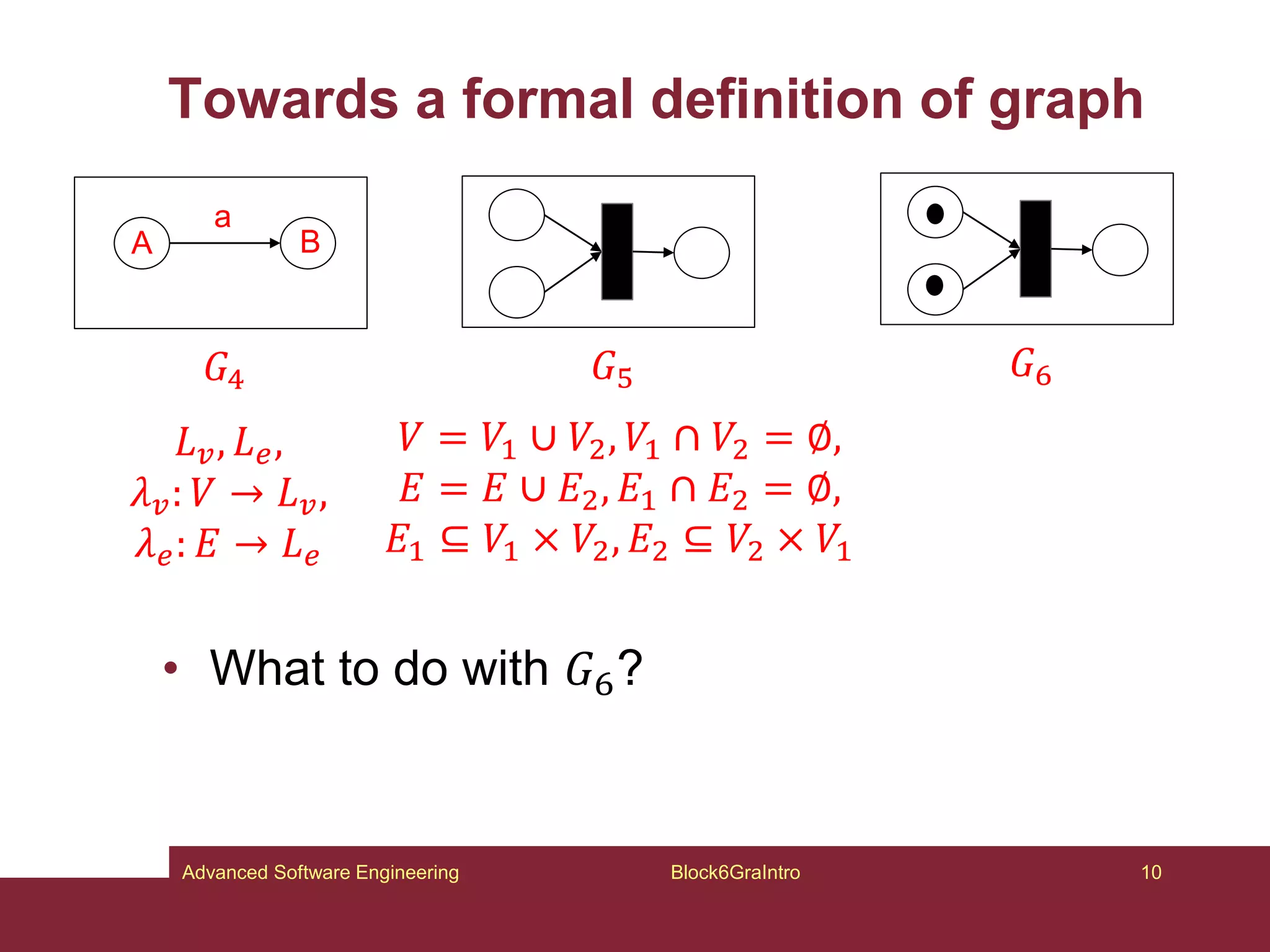
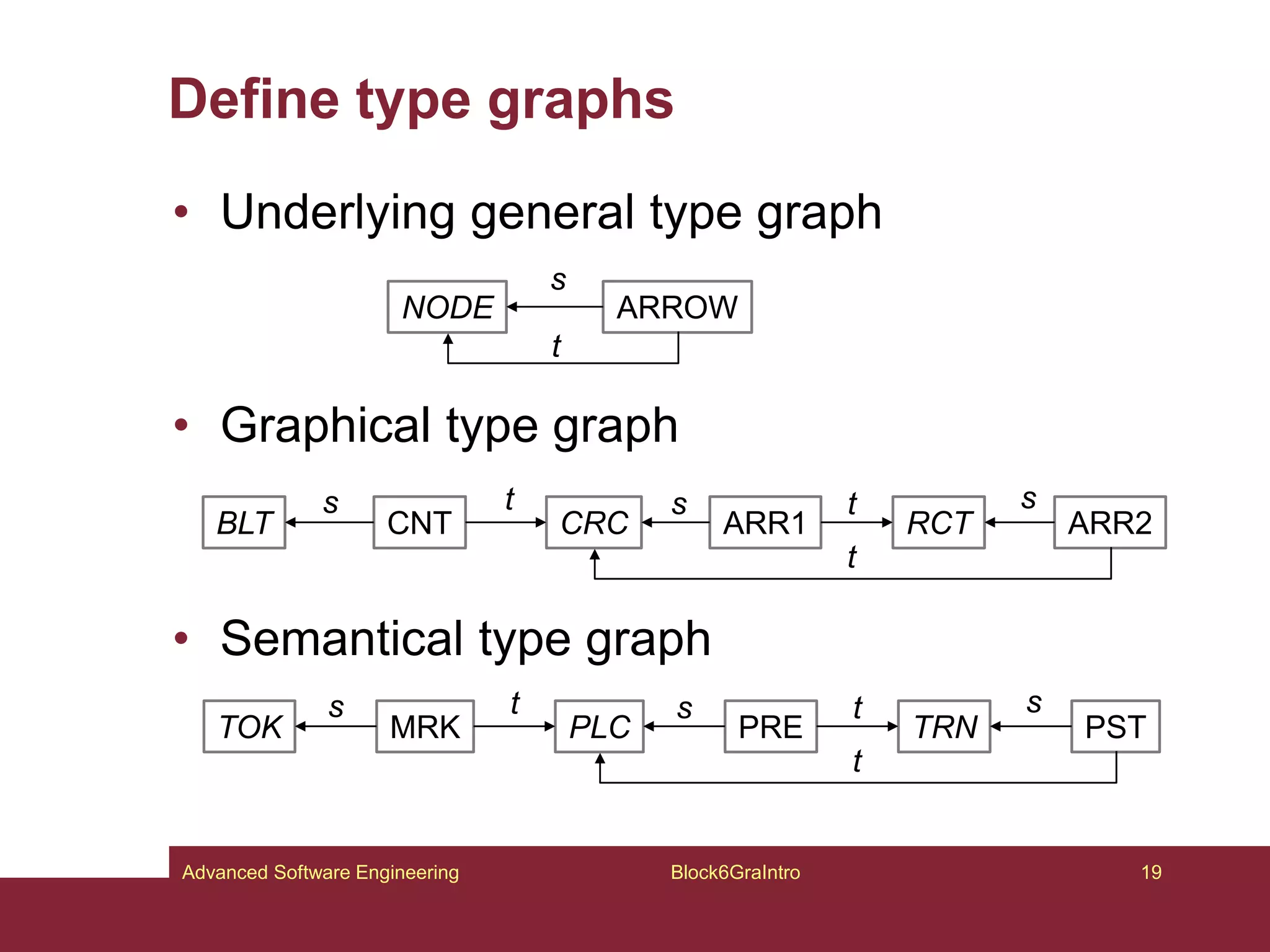
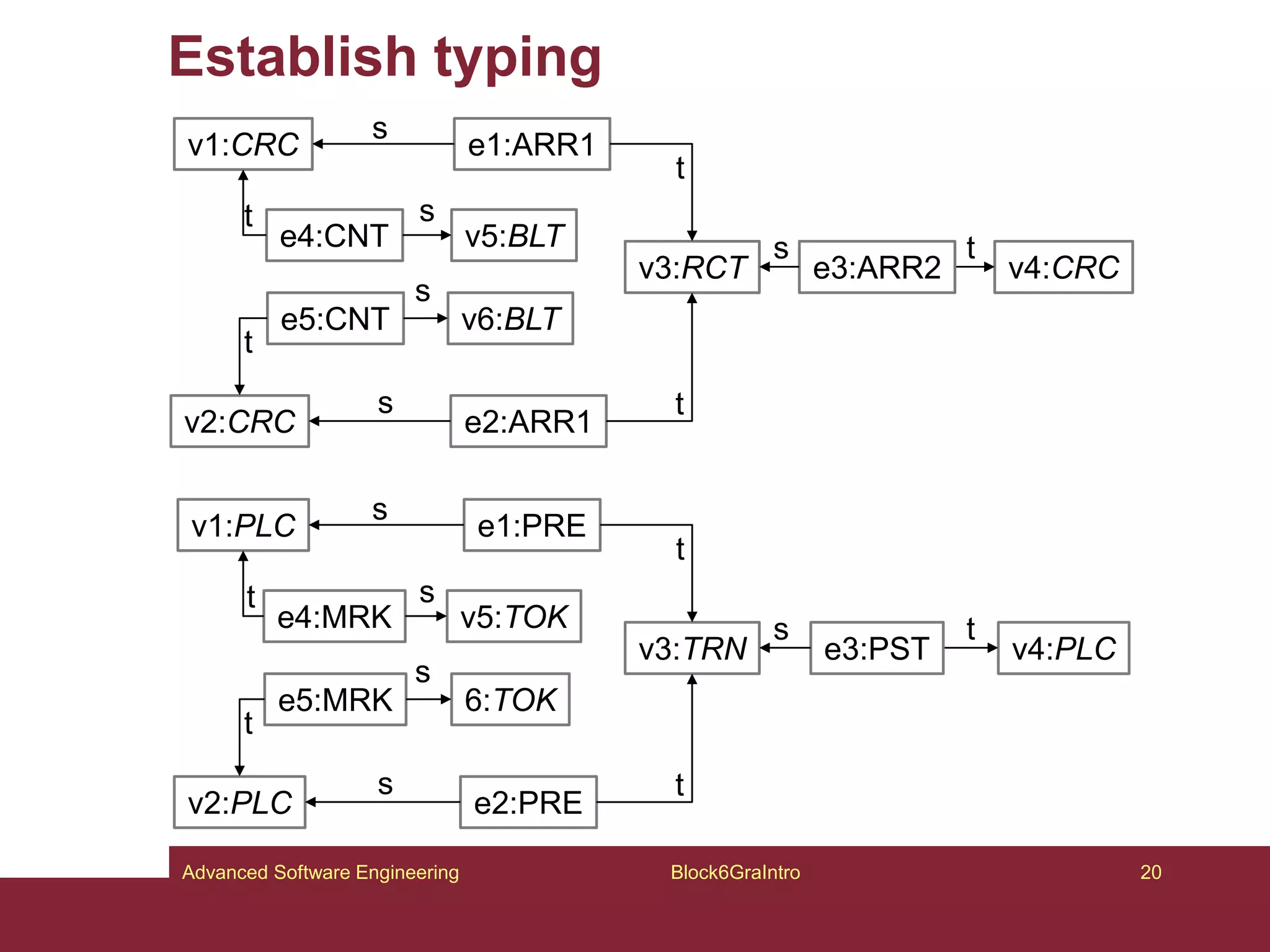
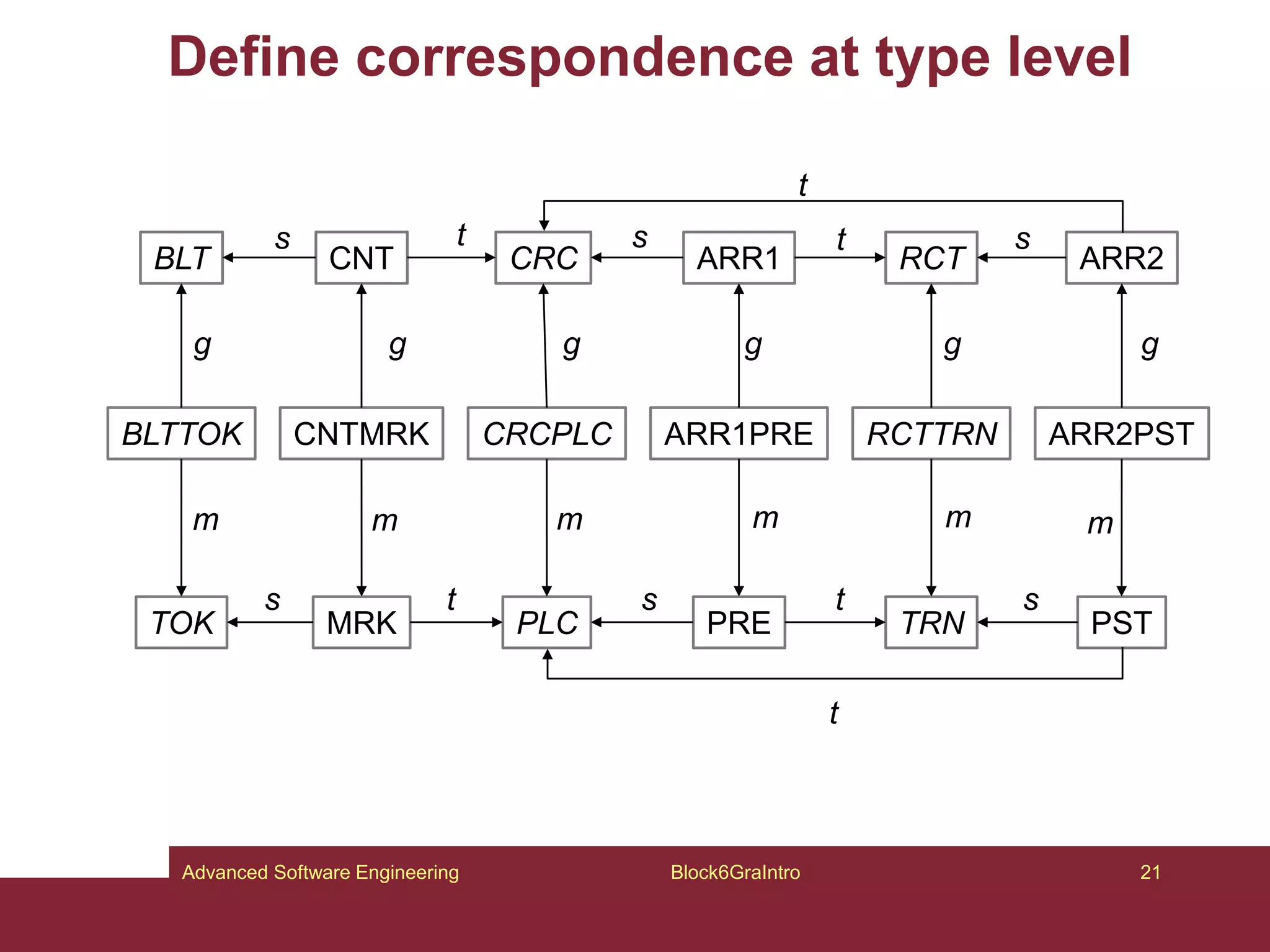
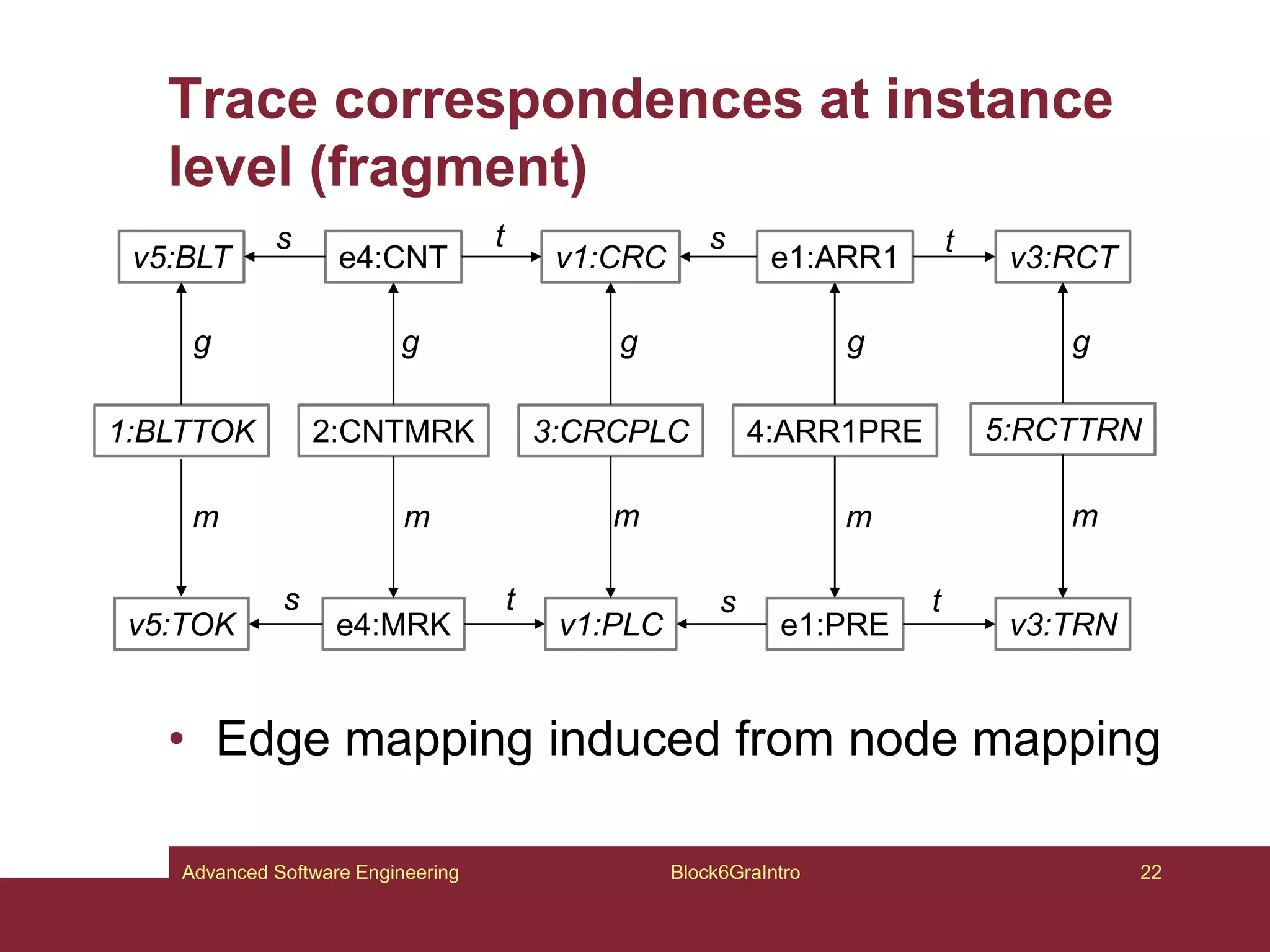
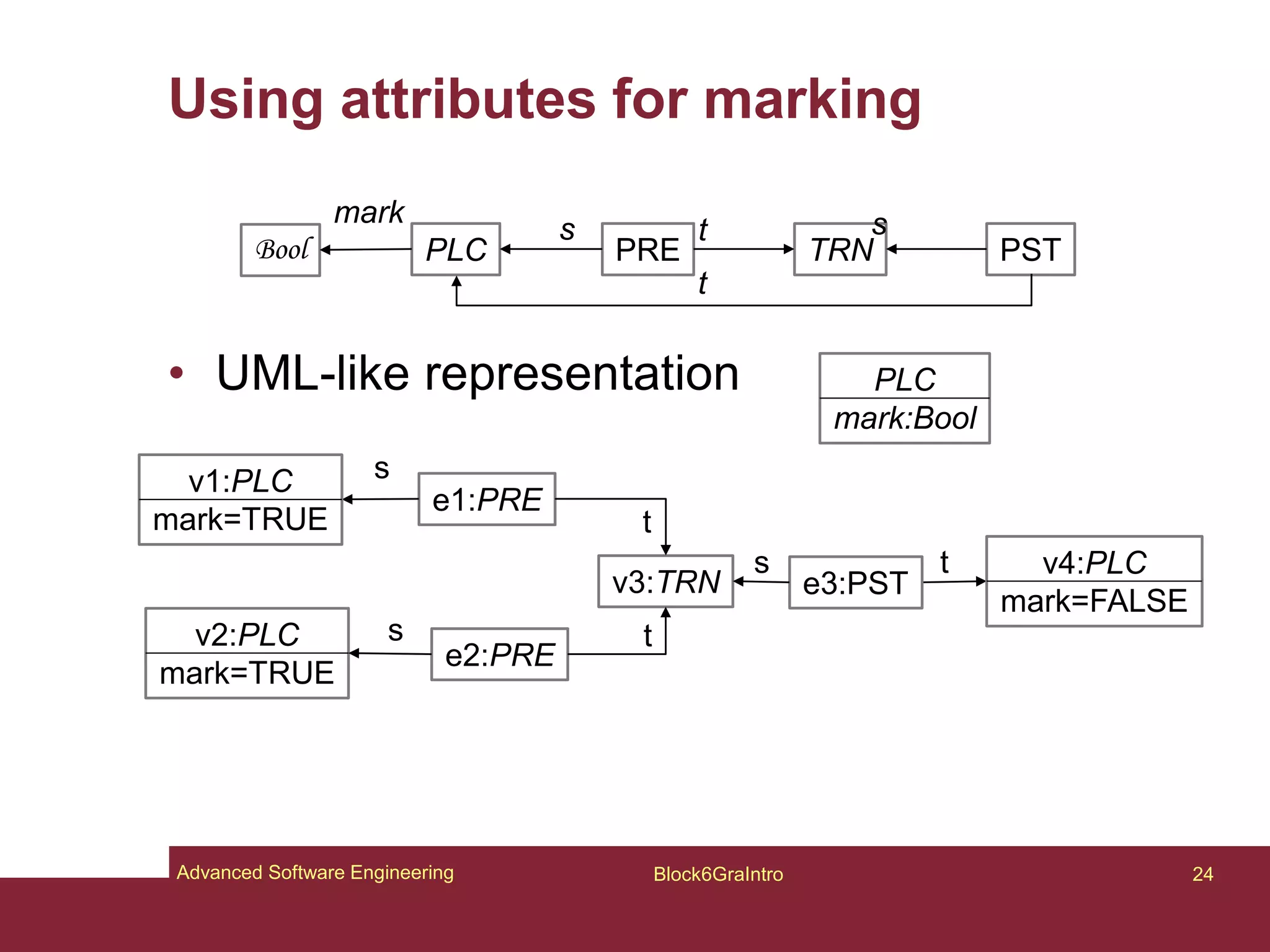
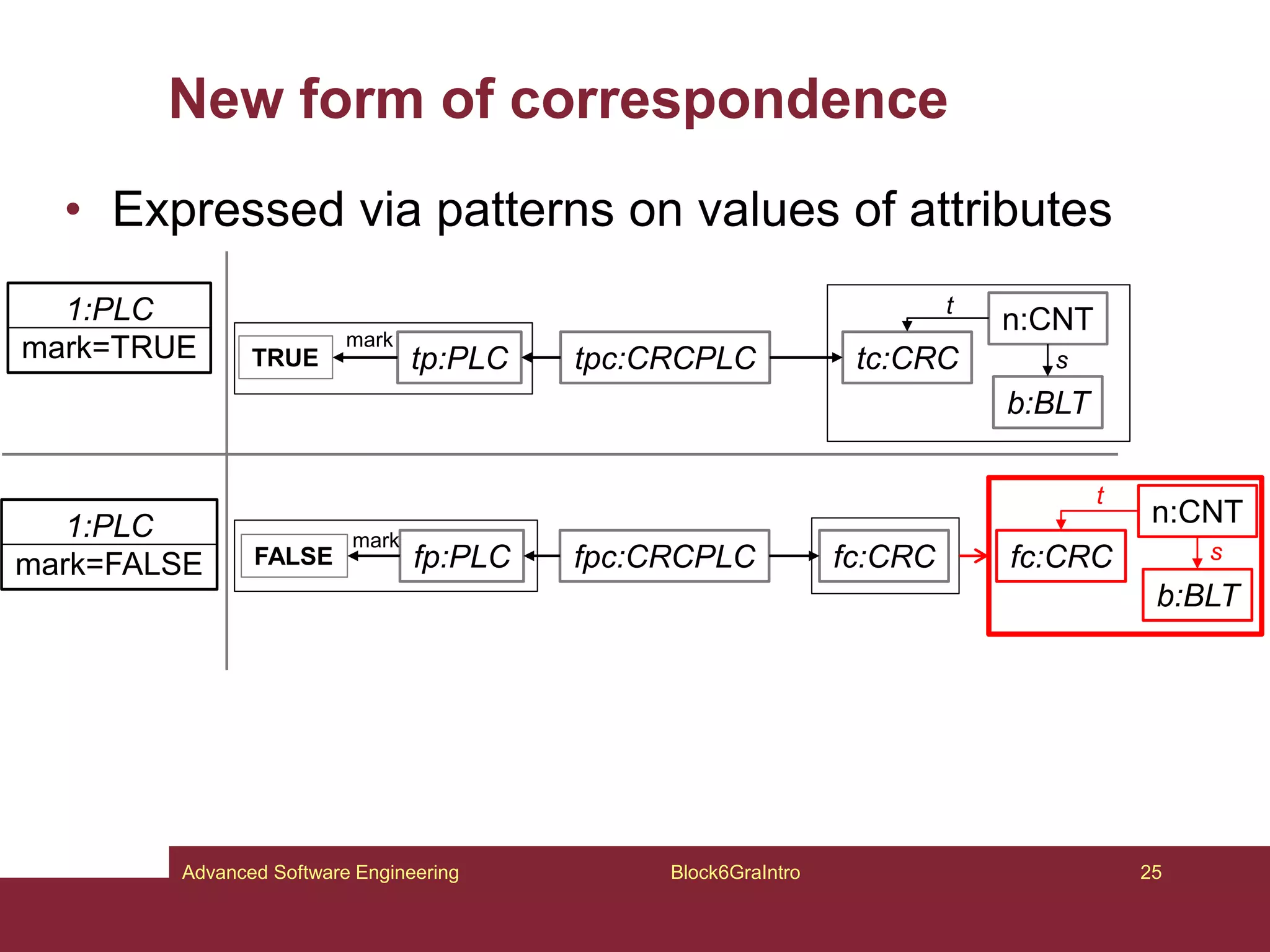
This document provides an introduction to graphs and graph-related concepts. It discusses different types of graphs, including labeled, typed, and attributed graphs. It also explores various definitions of graphs and considers whether certain structures qualify as graphs. The document examines computing with graphs, including dynamics and transformations on graphs. It proposes formal definitions of graphs and considers how to represent more complex structures like G6 as graphs. Finally, it discusses typed graphs and establishing correspondences between graphical and semantic relationships in graphs.

1. Advanced Software Engineering
Paolo Bottoni
Block 6: Introduction to graphs

2. Overview
• Introduction to graphs
• Computing with graphs
• Graphs as metamodels
Block6GraIntro 2
Advanced Software Engineering

3. Introduction to graphs
• Graphs
• Labelled
• Typed
• Attributed
• Examples of models
Block6GraIntro 3
Advanced Software Engineering

4. Graphs and graph-like structures
• What is a graph?
• Are these graphs?
Block6GraIntro 4
Advanced Software Engineering
𝐺1
𝐺3
𝐺2
𝐺4
A B
a
𝐺5 𝐺6

5. And can we have dynamics on graphs?
• Dynamics expressed as change in decoration
• Structure maintained
Block6GraIntro 5
Advanced Software Engineering
A B
a
abc
A B
a
bc

6. Dynamics in graph construction
• Languages of graphs, well-formedness
– Generating
– Parsing
– Membership problem
Block6GraIntro 6
Advanced Software Engineering

7. Computing with diagrams
• What is this?
• We need an interpretation
• Can we express it as a graph transformation?
Block6GraIntro 7
Advanced Software Engineering

8. Towards a formal definition of graph
• What is a graph?
𝐺 = 𝑉, 𝐸 , 𝐸 ⊆ 𝑉 × 𝑉
• Simple? Think again
• Are these graphs?
Block6GraIntro 8
Advanced Software Engineering
𝐺1
𝐺3
𝐸 ∈ ℘2
(𝑉) 𝐸 ∈ 𝑚℘2
(𝑉)
𝐸 ⊆ 𝑀𝑆𝐸𝑇(𝑉 × 𝑉)
𝐺2

9. An alternative view of nondirected graphs
Block6GraIntro 9
Advanced Software Engineering
𝐺1
′ 𝐺3
′
𝐸 ⊆ 𝑉 × 𝑉 𝐸 ⊆ 𝑀𝑆𝐸𝑇(𝑉 × 𝑉)

10. Towards a formal definition of graph
• What to do with 𝐺6?
Block6GraIntro 10
Advanced Software Engineering
𝐿𝑣, 𝐿𝑒,
𝜆𝑣: 𝑉 → 𝐿𝑣,
𝜆𝑒: 𝐸 → 𝐿𝑒
𝐺4
A B
a
𝐺5 𝐺6
𝑉 = 𝑉1 ∪ 𝑉2, 𝑉1 ∩ 𝑉2 = ∅,
𝐸 = 𝐸 ∪ 𝐸2, 𝐸1 ∩ 𝐸2 = ∅,
𝐸1 ⊆ 𝑉1 × 𝑉2, 𝐸2 ⊆ 𝑉2 × 𝑉1

11. A more general definition of graph
• 𝐺 = 𝑉, 𝐸, 𝑠, 𝑡 , 𝑉 ∩ 𝐸 = ∅, 𝑠, 𝑡: 𝐸 → 𝑉
• Are 𝐺1, … , 𝐺3 all graphs under this new definition?
𝐺1 = ( 𝑣1, 𝑣2 , 𝑒1, 𝑒2 , 𝑠 = (𝑒1, 𝑣1 , (𝑒2 , 𝑣2)}, 𝑡 = { 𝑒1, 𝑣2 , (𝑒2, 𝑣1)}
𝐺2 = ( 𝑣1, 𝑣2 , 𝑒1, 𝑒2 , 𝑠 = (𝑒1, 𝑣1 , (𝑒2 , 𝑣1)}, 𝑡 = { 𝑒1, 𝑣2 , (𝑒2, 𝑣2)}
𝐺3 = 𝑣1, 𝑣2 , 𝑒1, 𝑒2, 𝑒3, 𝑒4 , 𝑠 = (𝑒1, 𝑣1 , (𝑒2 , 𝑣1 , 𝑒3, 𝑣2 , (𝑒4, 𝑣2)},
𝑡 = { 𝑒1, 𝑣2 , 𝑒2, 𝑣2 , 𝑒3, 𝑣1 , (𝑒4, 𝑣1)}
• We do not need multisets!
Block6GraIntro 11
Advanced Software Engineering

12. Adding labels and partitioning
𝐺 = 𝑉, 𝐸, 𝐿𝑣, 𝐿𝑒, 𝜆𝑣: 𝑉 → 𝐿𝑣, 𝜆𝑒: 𝐸 → 𝐿𝑒
𝐺 = (𝑉1 ∪ 𝑉2, 𝐸1 ∪ 𝐸2, 𝑠1 ∪ 𝑠2, 𝑡1 ∪ 𝑡2)
• Also: 𝐺 = 𝑉1 ∪ 𝑉2, 𝐸, 𝑠, 𝑡 , 𝑠, 𝑡: 𝐸 → 𝑉,
𝑠 𝑒 ∈ 𝑉1 ⇒ 𝑡 𝑒 ∈ 𝑉2, 𝑠 𝑒 ∈ 𝑉2 ⇒ 𝑡 𝑒 ∈ 𝑉1
𝐺4 = ( 𝑣1, 𝑣2 , 𝑒1 , 𝐿𝑣 = 𝐴, 𝐵 , 𝐿𝑒 = 𝑎 , 𝑠 = 𝑒1, 𝑣1 ,
𝑡 = 𝑒1, 𝑣2 , 𝜆𝑣 = 𝑣1, 𝐴 , 𝑣2, 𝐵 , 𝜆𝑒 = 𝑒1, 𝑎
𝐺5 = ( 𝑣1, 𝑣2, 𝑣4 ∪ 𝑣3 , 𝑒1, 𝑒2} ∪ {𝑒3 ,
𝑠 = 𝑒1, 𝑣1 , 𝑒2, 𝑣2 , 𝑒3, 𝑣3 ,
𝑡 = { 𝑒1, 𝑣3 , 𝑒2, 𝑣3 , 𝑒3, 𝑣4 }
Block6GraIntro 12
Advanced Software Engineering

13. What do we need to see 𝑮𝟔 as a graph?
• Abstract graphs!!!
• We are interested in relationships
• Graphical relationships
• Semantic relationships
Block6GraIntro 13
Advanced Software Engineering

14. But for that …
• We need typed graphs
𝐺𝑇 = 𝐺, 𝑇𝑉 ∪ 𝑇𝐸, 𝜏𝑉, 𝜏𝐸
𝑇𝑉 ∩ 𝑇𝐸 = ∅, 𝜏𝑣: 𝑉 → 𝑇𝑉, 𝜏𝑒: 𝐸 → 𝑇𝐸
• More on that later ….
Block6GraIntro 14
Advanced Software Engineering

15. Graphical relationships
Block6GraIntro 15
Advanced Software Engineering
𝐺6
𝐺6
𝑔𝑟𝑝
= (𝑉5 ∪ 𝑣5, 𝑣6 , 𝐸5 ∪ 𝑒4, 𝑒5 ,
𝑠 = 𝑠5 ∪ { 𝑒4, 𝑣5 , (𝑒5, 𝑣6)}, 𝑡 = 𝑡5 ∪ { 𝑒4, 𝑣1 , (𝑒5, 𝑣2)},
𝐶𝑅𝐶, 𝑅𝐶𝑇, 𝐵𝐿𝑇} ∪ {𝐴𝑅𝑅1, 𝐴𝑅𝑅2, 𝐶𝑁𝑇 ,
𝜏𝑉 = 𝑣1, 𝐶𝑅𝐶), (𝑣2, 𝐶𝑅𝐶}, (𝑣4, 𝐶𝑅𝐶 , 𝑣3, 𝑅𝐶𝑇 , 𝑣5, 𝐵𝐿𝑇 , (𝑣6, 𝐵𝐿𝑇) ,
𝜏𝑒 = (𝑒1, 𝐴𝑅𝑅1), 𝑒2, 𝐴𝑅𝑅1 (𝑒3, 𝐴𝑅𝑅2), 𝑒4, 𝐶𝑁𝑇 , (𝑒5, 𝐶𝑁𝑇) )

16. Semantical relationships
Block6GraIntro 16
Advanced Software Engineering
𝐺6
𝐺6
𝑠𝑒𝑚
= (𝑉5 ∪ 𝑣5, 𝑣6 , 𝐸5 ∪ 𝑒4, 𝑒5 ,
𝑠 = 𝑠5 ∪ { 𝑒4, 𝑣5 , (𝑒5, 𝑣6)}, 𝑡 = 𝑡5 ∪ { 𝑒4, 𝑣1 , (𝑒5, 𝑣2)},
𝑃𝐿𝐶, 𝑇𝑅𝑁, 𝑇𝑂𝐾} ∪ {𝑃𝑅𝐸, 𝑃𝑆𝑇, 𝑀𝑅𝐾 ,
𝜏𝑉 = 𝑣1, 𝑃𝐿𝐶), (𝑣2, 𝑃𝐿𝐶}, (𝑣4, 𝑃𝐿𝐶 , 𝑣3, 𝑇𝑅𝑁 , 𝑣5, 𝑇𝑂𝐾 , (𝑣6, 𝑇𝑂𝐾) ,
𝜏𝑒 = (𝑒1, 𝑃𝑅𝐸), 𝑒2, 𝑃𝑅𝐸 (𝑒3, 𝑃𝑆𝑇), 𝑒4, 𝑀𝑅𝐾 , (𝑒5, 𝑀𝑅𝐾) )

17. Graphical-semantical mapping
Block6GraIntro 17
Advanced Software Engineering
𝑉𝑔𝑟𝑝 ↔ 𝑉𝑠𝑒𝑚, 𝐸𝑔𝑟𝑝 ↔ 𝐸𝑠𝑒𝑚, 𝑠𝑔𝑟𝑝 ↔ 𝑠𝑠𝑒𝑚, 𝑡𝑔𝑟𝑝 ↔ 𝑡𝑠𝑒𝑚,
𝑇𝑉
𝑔𝑠
= 𝐶𝑅𝐶, 𝑃𝐿𝐶 , 𝑅𝐶𝑇, 𝑇𝑅𝑁 , 𝐵𝐿𝑇, 𝑇𝑂𝐾 ,
𝑇𝐸
𝑔𝑠
= 𝐴𝑅𝑅1, 𝑃𝑅𝐸 , 𝐴𝑅𝑅2, 𝑃𝑆𝑇 , (𝐶𝑁𝑇, 𝑀𝑅𝐾)
𝜏𝑉
𝑔𝑠
and 𝜏𝐸
𝑔𝑠
induced by correspondences above

18. Can we do this graphically?
• Define a type graph
• Establish typing
• Define correspondence at type level
• Trace correspondence at instance level
Block6GraIntro 18
Advanced Software Engineering

19. Define type graphs
• Underlying general type graph
• Graphical type graph
• Semantical type graph
Block6GraIntro 19
Advanced Software Engineering
PRE TRN
PLC PST
MRK
TOK
s s
s
t
t
t
ARROW
NODE
s
t
ARR1 RCT
CRC ARR2
CNT
BLT
s s
s
t
t
t

20. Establish typing
Block6GraIntro 20
Advanced Software Engineering
e1:ARR1
v2:CRC
v4:CRC
v3:RCT
v1:CRC
e2:ARR1
e3:ARR2
e4:CNT v5:BLT
e5:CNT v6:BLT
s
s
s
s
s
t
t
t
t
t
e1:PRE
v2:PLC
v4:PLC
v3:TRN
v1:PLC
e2:PRE
e3:PST
e4:MRK v5:TOK
e5:MRK 6:TOK
s
s
s
s
s
t
t
t
t
t

21. Define correspondence at type level
Block6GraIntro 21
Advanced Software Engineering
PRE TRN
PLC PST
MRK
TOK
s s
s
t
t
t
ARR1 RCT
CRC ARR2
CNT
BLT
s s
s
t
t
t
ARR1PRE RCTTRN
CRCPLC ARR2PST
CNTMRK
BLTTOK
g
m
g g g g g
m m m m m

22. Trace correspondences at instance
level (fragment)
• Edge mapping induced from node mapping
Block6GraIntro 22
Advanced Software Engineering
e1:PRE v3:TRN
v1:PLC
e4:MRK
v5:TOK
s
s t
t
e1:ARR1 v3:RCT
v1:CRC
e4:CNT
v5:BLT
s
s t
t
4:ARR1PRE 5:RCTTRN
3:CRCPLC
2:CNTMRK
1:BLTTOK
g
m
g g g g
m m m m

23. Do we need the MARK type?
• Attributed graphs
𝐺 = 𝑉 ∪ 𝑉𝐴, 𝐸 ∪ 𝐸𝐴, 𝑠, 𝑡, 𝑁𝑚𝑠, 𝜆𝐸: 𝐸𝐴 → 𝑁𝑚𝑠
∀𝑒𝐴 ∈ 𝐸𝐴, 𝑠 𝑒 ∈ 𝑉, 𝑡 𝑒 ∈ 𝑉
𝑠
• Usually coupled with types
𝐺 = (𝑉 ∪ 𝑉𝐴, 𝐸 ∪ 𝐸𝐴, 𝑠, 𝑡, 𝑇𝑉, 𝑇𝐸, 𝑇𝐴, 𝑁𝑚𝑠, 𝜏𝑉, 𝜏𝐸,
𝜏𝐴: 𝑉𝐴 → 𝑇𝐴, 𝜆𝐸: 𝐸𝐴 → 𝑁𝑚𝑠)
∀𝑒 ∈ 𝐸𝐴, 𝑠 𝑒 = 𝑣, 𝜆𝐸 𝑒 = 𝑛𝑚, 𝑡 𝑒 = 𝑣𝑙, 𝜏𝑉 𝑣 = 𝑡𝑝1,
𝜏𝐴 𝑣𝑙 = 𝑡𝑝2 ⇒ ∀𝑣′ ∈ 𝑉, 𝜏𝑉 𝑣′ = 𝑡𝑝1,
∃𝑒′ ∈ 𝐸𝐴, ∃𝑣𝑙′ ∈ 𝑉𝐴, 𝑠 𝑒′ = 𝑣′, 𝑡 𝑒′ = 𝑣𝑙′,
𝜆𝐸 𝑒′ = 𝑛𝑚, 𝜏𝑠 𝑣𝑙′ = 𝑡
Block6GraIntro 23
Advanced Software Engineering
5
sz

24. Using attributes for marking
• UML-like representation
Block6GraIntro 24
Advanced Software Engineering
PRE TRN
PLC PST
Bool
s s
mark
t
t
PLC
mark:Bool
e1:PRE
v3:TRN
v2:PLC
mark=TRUE
e2:PRE
e3:PST
s
s
s
t
t
v1:PLC
mark=TRUE
t
v4:PLC
mark=FALSE

25. New form of correspondence
• Expressed via patterns on values of attributes
Block6GraIntro 25
Advanced Software Engineering
1:PLC
mark=TRUE
1:PLC
mark=FALSE
tp:PLC
TRUE
mark
fp:PLC
FALSE
mark
tpc:CRCPLC
fpc:CRCPLC
n:CNT
b:BLT
s
tc:CRC
fc:CRC
n:CNT
b:BLT
s
fc:CRC
t
t

26. What is left to do
• Defining languages
– Graph grammars
– Wellformedness constraint
– Controlling parsing
• Defining dynamics
– Graph transformations
– Application conditions
– Controlling transformations
Block6GraIntro 26
Advanced Software Engineering