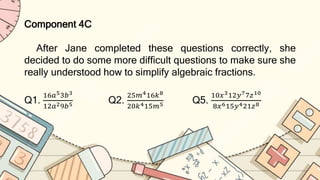
This document contains lessons on simplifying rational algebraic expressions. It includes examples of expressions to simplify, definitions of key terms used in simplification like common factor and cancel, and practice questions for students to consolidate their skills in simplifying fractions. One section involves word problems about a cook determining how many boxes of vegetables are needed to make soup for a certain number of restaurant guests.

1. Simplifies
Rational
Algebraic
Expressions
Lesson 3

2. Component 1: Short Review
Simplify these expressions as far as possible:
Q1.
8
20
Q2.
12𝑥
3
Q3.
6𝑥
12𝑥𝑦
Q4.
16𝑥2
24𝑥3𝑦4

3. Component 3: Lesson Language Practice
Simplify – reduce the expression into a simpler form.
Expression – a set of terms combined using the four
operations.
Cancel – simplify a fraction by dividing both top and
bottom by the same amount.
Common factor – numbers or terms that divide exactly
into another number or expression.

4. Component 4: Lesson Activity
Component 4A
Jane wants to practice her algebraic fraction skills. Her
teacher suggested she do some extra problems to help
consolidate her skills. Jane practiced and practiced lots of
questions until she could confidently simplify a number of
algebraic fractions into their simplest form.

5. Component 4A
Simplify each algebraic fraction:
Q1.
18𝑎
24
Q2.
28𝑏𝑥
8𝑥
Q3.
27𝑥2
18𝑥
Q4.
30𝑎2
25𝑎2
Q5.
12𝑥5𝑦3
15𝑥4𝑦6

6. Component 4C
After Jane completed these questions correctly, she
decided to do some more difficult questions to make sure she
really understood how to simplify algebraic fractions.
Q1.
16𝑎53𝑏3
12𝑎29𝑏5 Q2.
25𝑚416𝑘8
20𝑘415𝑚5 Q5.
10𝑥312𝑦77𝑧10
8𝑥615𝑦421𝑧8

7. Solves
Problems with
Rational
Expressions
Lesson 4

8. Component 1: Short Review
Simplify these expressions as far as possible:
Q1.
6𝑥
12𝑥𝑦
Q2.
𝑥
3
+
2𝑥
5
Q3.
3𝑥−6
5
−
2𝑥+1
3
Q4.
3
2𝑥
−
𝑦+1
3𝑥𝑦

9. Component 3: Lesson Language Practice
Simplify – reduce the expression into a simpler form.
Expression – a set of terms combined using the four
operations.
Cancel – simplify a fraction by dividing both top and
bottom by the same amount.
Common factor – numbers or terms that divide exactly
into another number or expression.

10. Component 4: Lesson Activity
Component 4A
Joe is a cook in a restaurant. Joes uses algebraic
expressions and formulate to determine many boxes of
vegetables he needs to buy to cook his meals each right. The
number of boxes of vegetables determines how much soup
he can cook.
On a particular night, Joe intends to make carrot soup.
The number of boxes Joe will need is determined by the
expression:
𝟑𝒙−𝟔
𝟓
−
𝟐𝒙+𝟏
𝟑
Where y is the number of boxes of carrots.

11. Component 4B
Q1. Simplify this expression.
Q2. There are 51 people booked into the restaurant that
night. If each person has carrot soup how many boxes of
carrots will Joe require?
Q3. On a previous night, Joe purchased 125 boxes of
carrots. How many people was he expecting at the
restaurant?

12. Component 4C
Joe decided to cook potato soup to include in his menu at
the restaurant. The number of potato soups that can be
cooked was determined by the expression:
𝟐𝒙+𝟏
𝟓
−
𝒙−𝟏
𝟐
Q1. Simplify this expression.
Q2. There are 60 people booked into the restaurant that
night. How many boxes of potatoes will Joe require if every
person has potato soup?
Q3. Joe buys 40 boxes of potatoes. How many people will be
able to have potato soup?