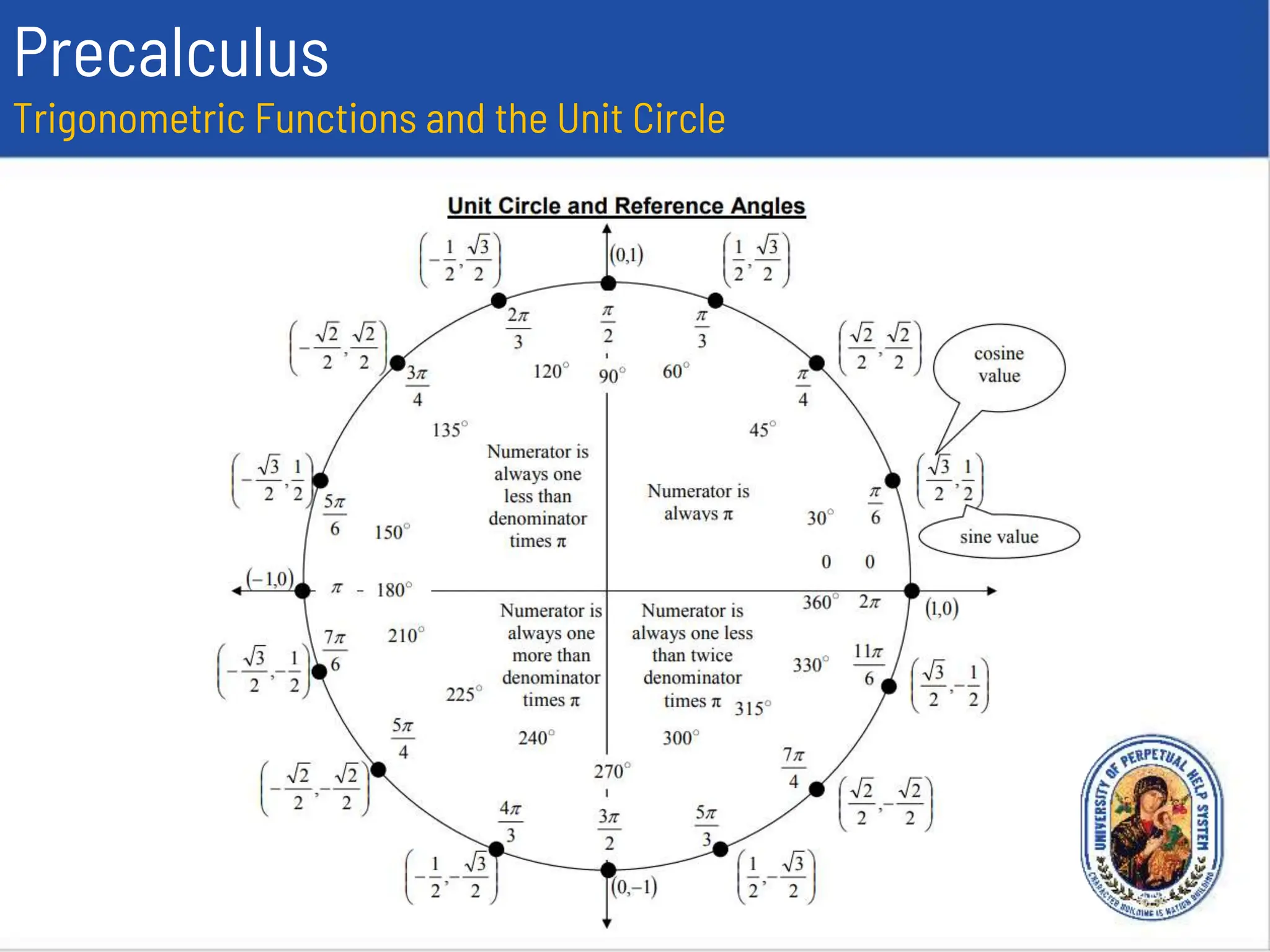
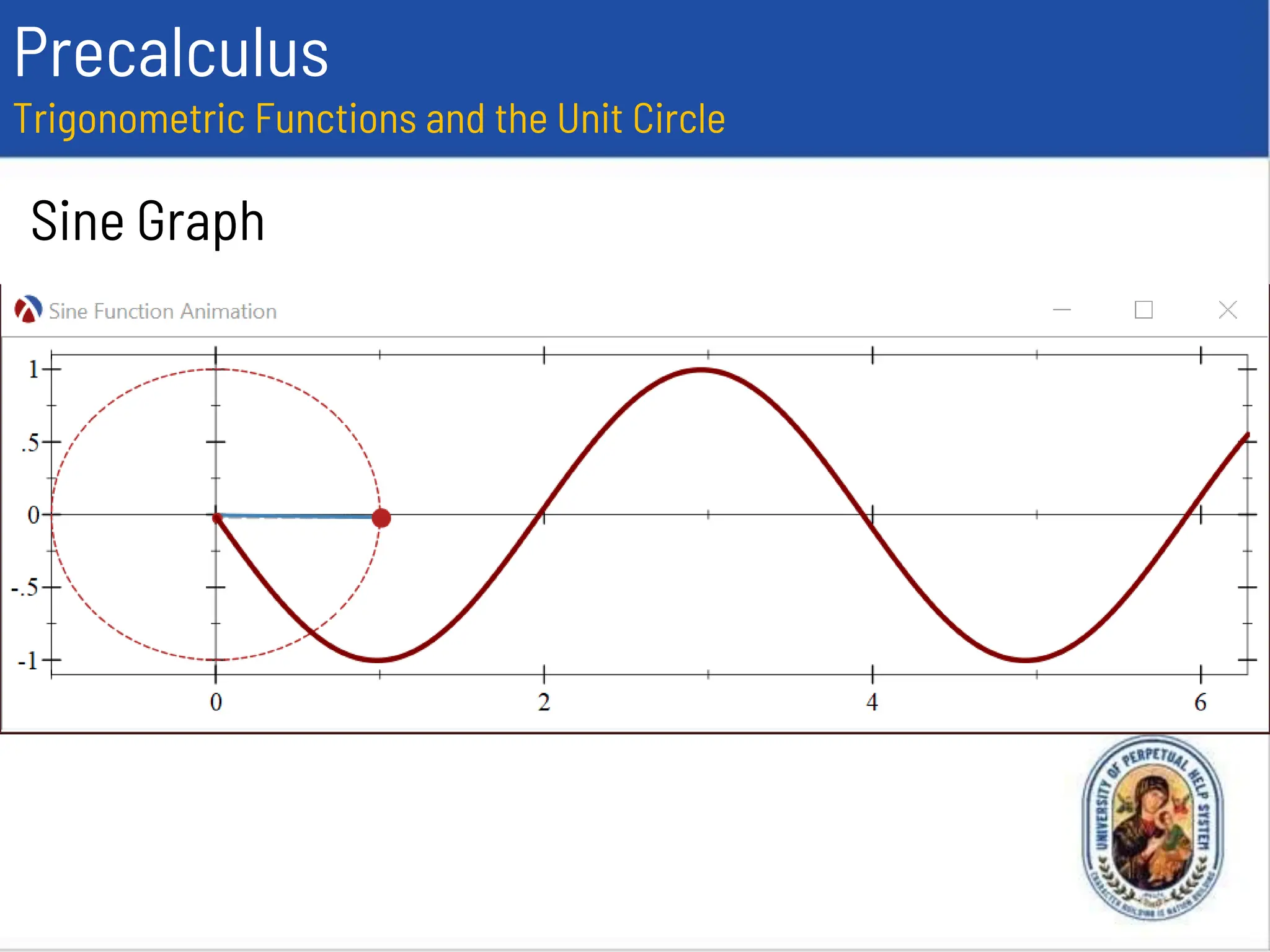
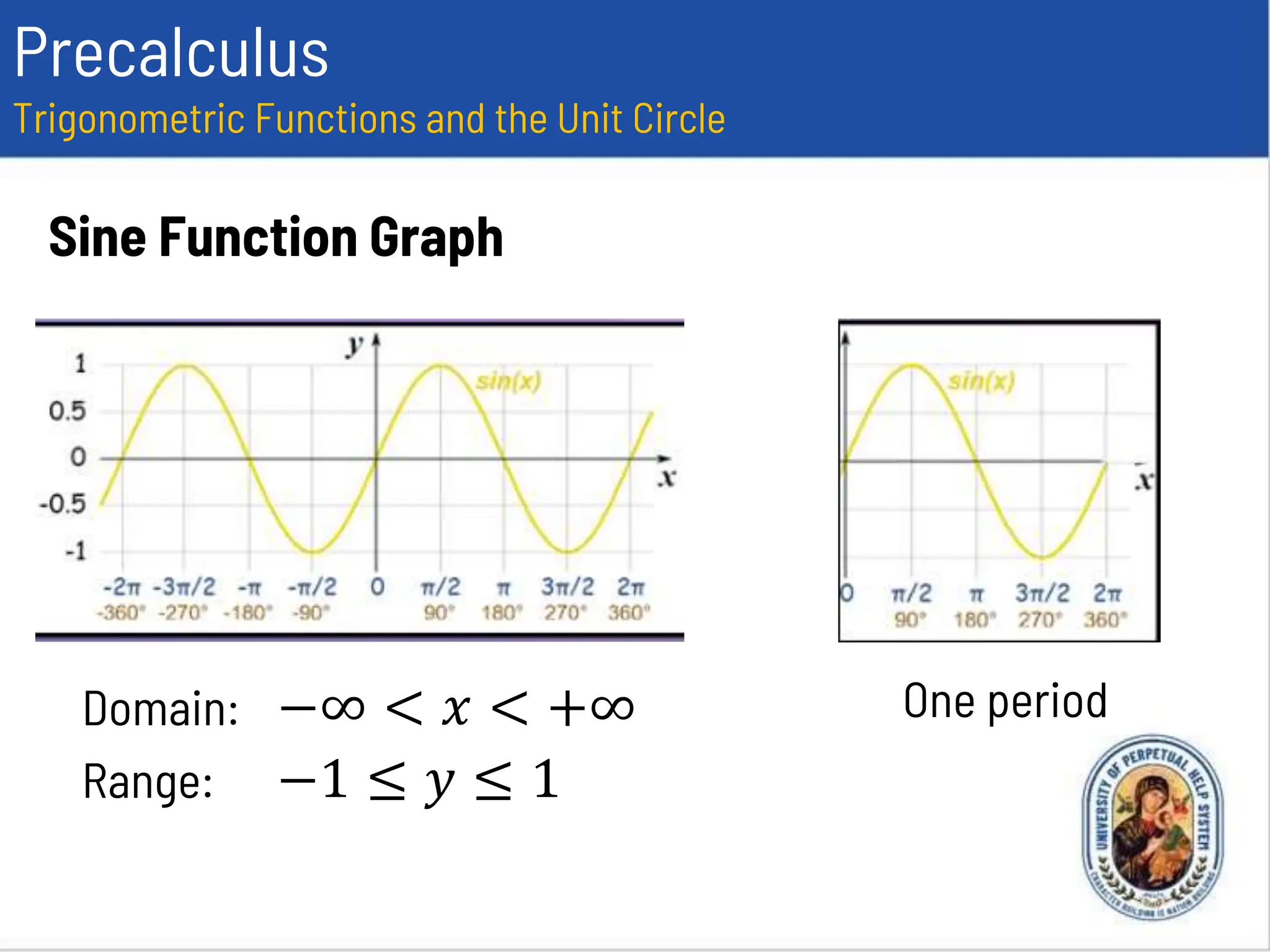
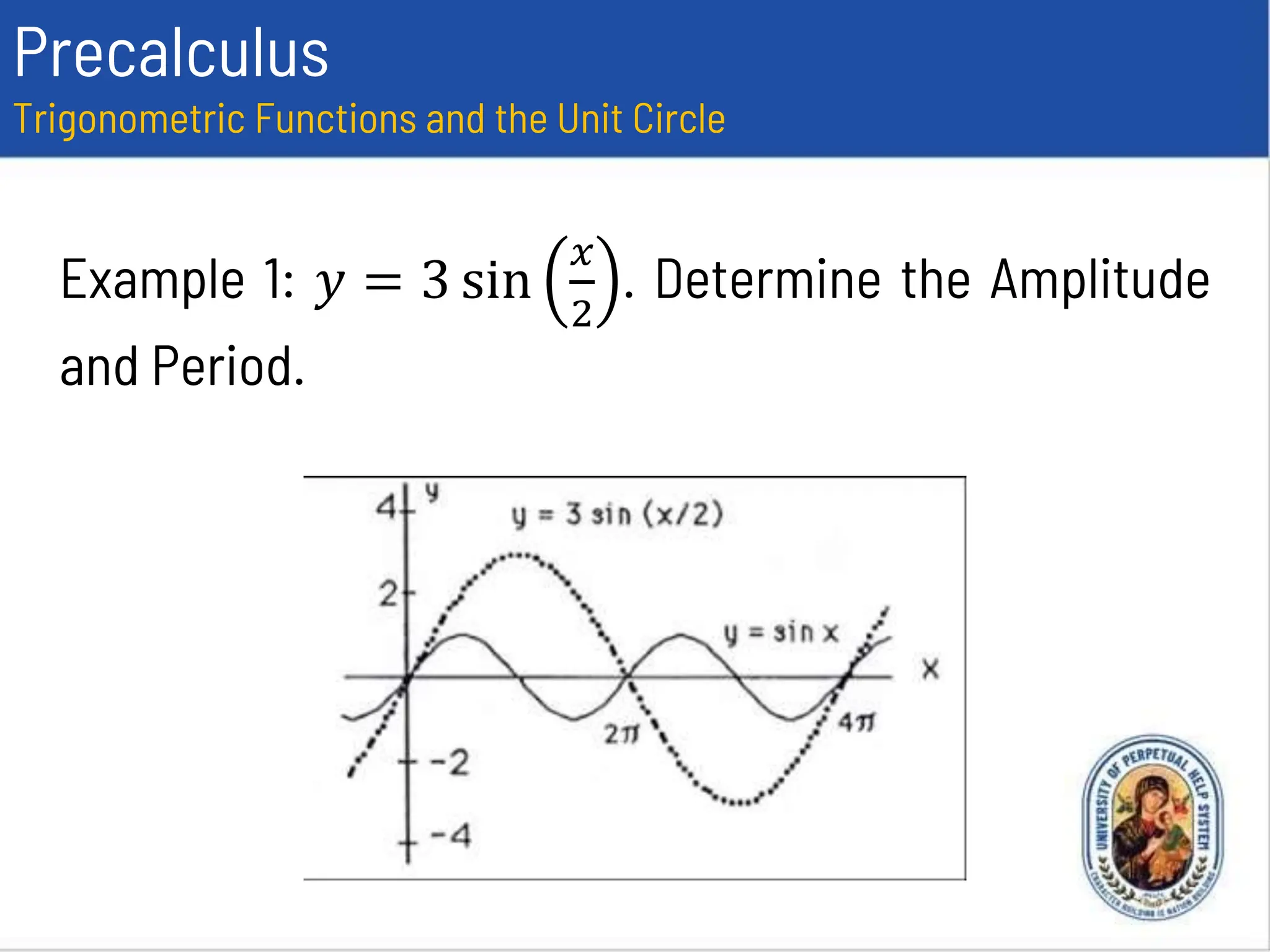
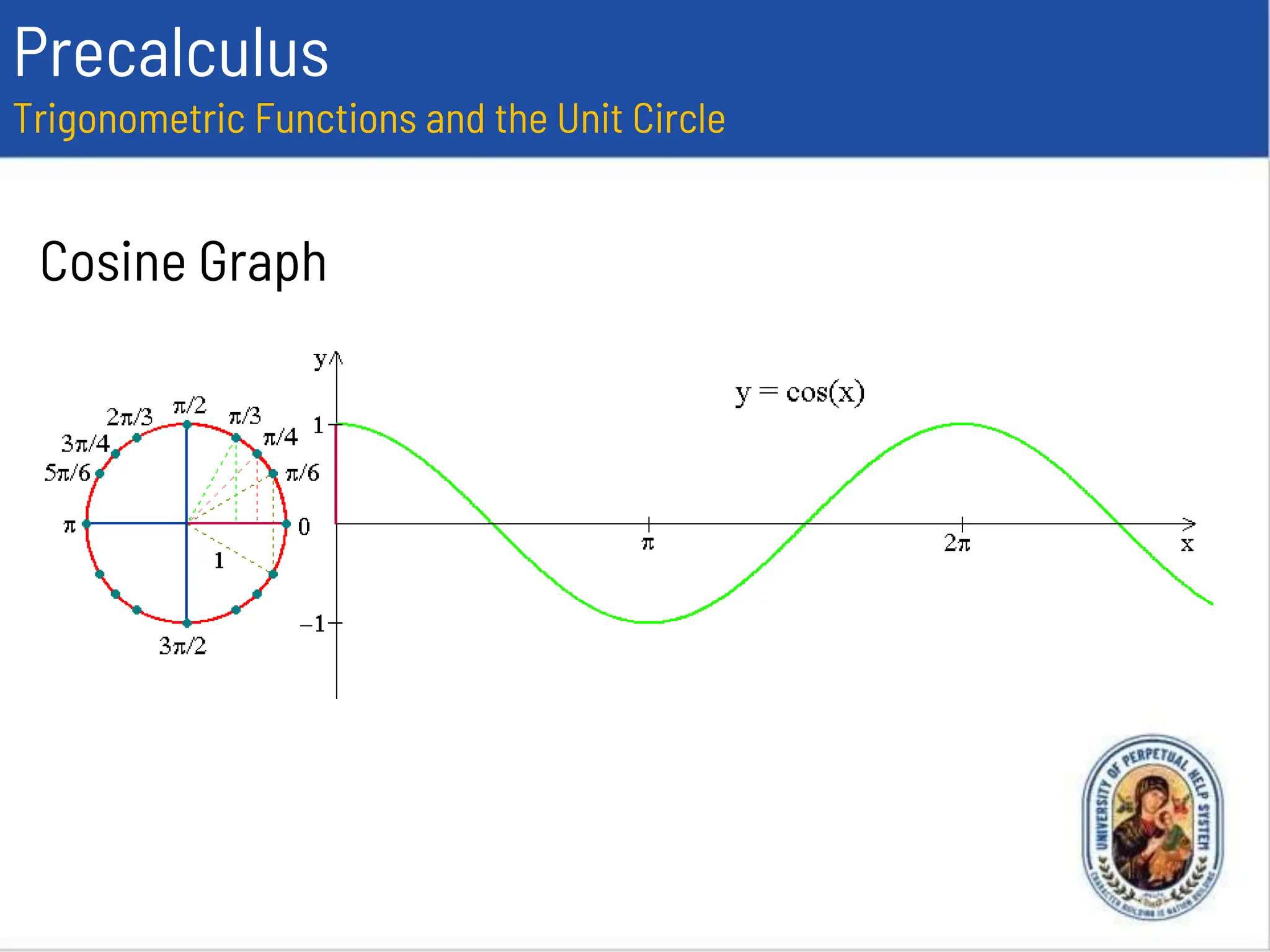
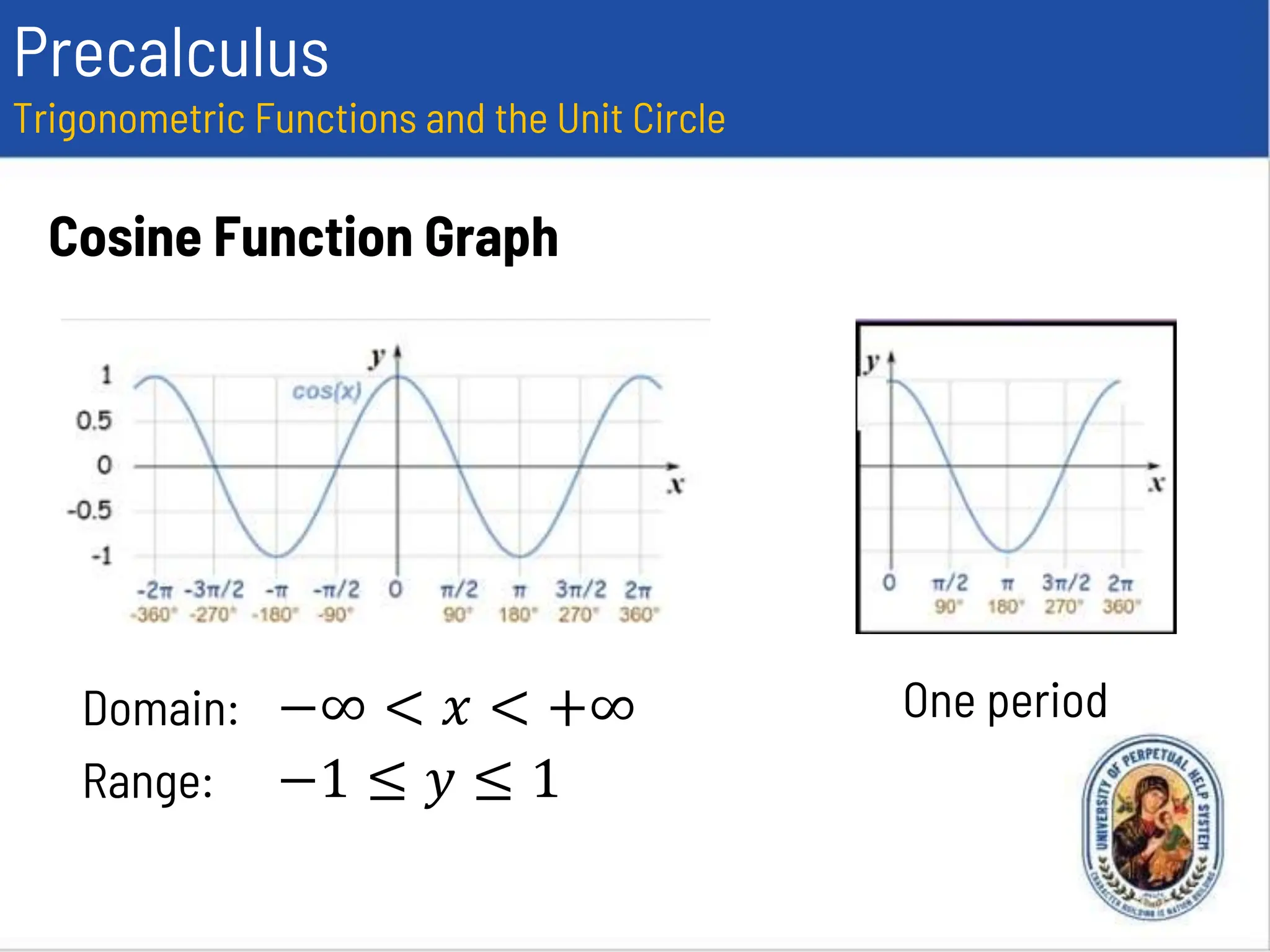
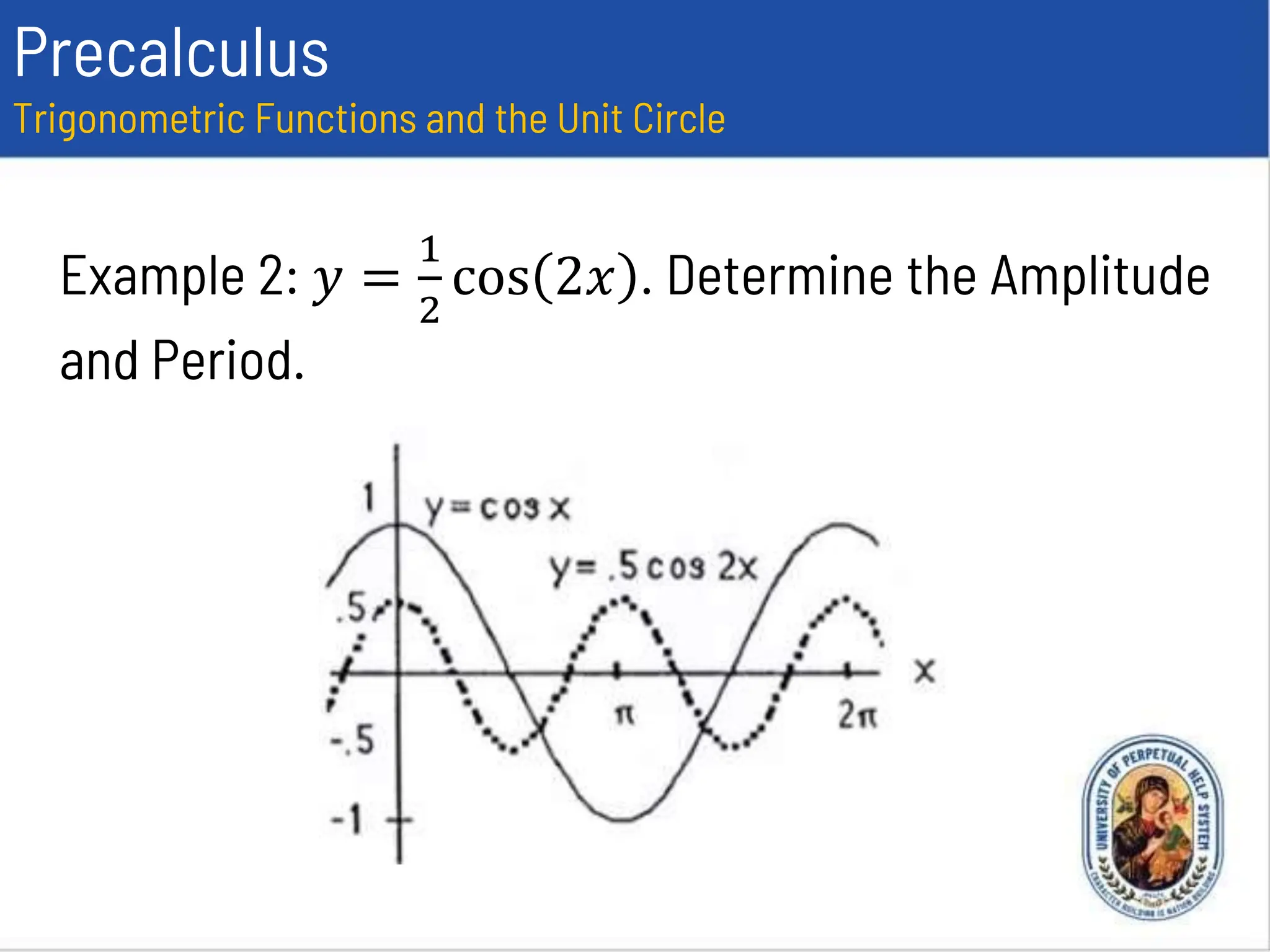
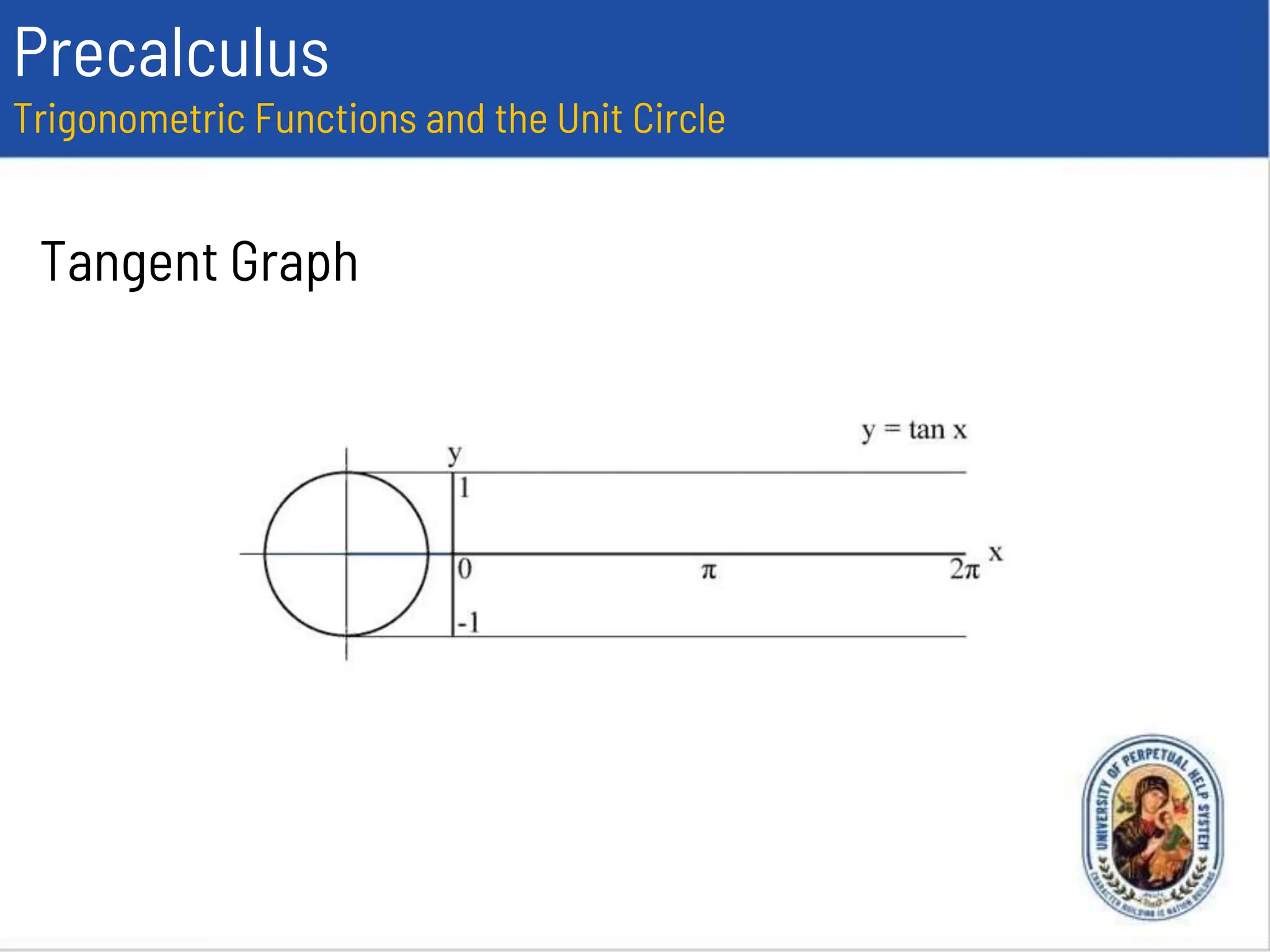
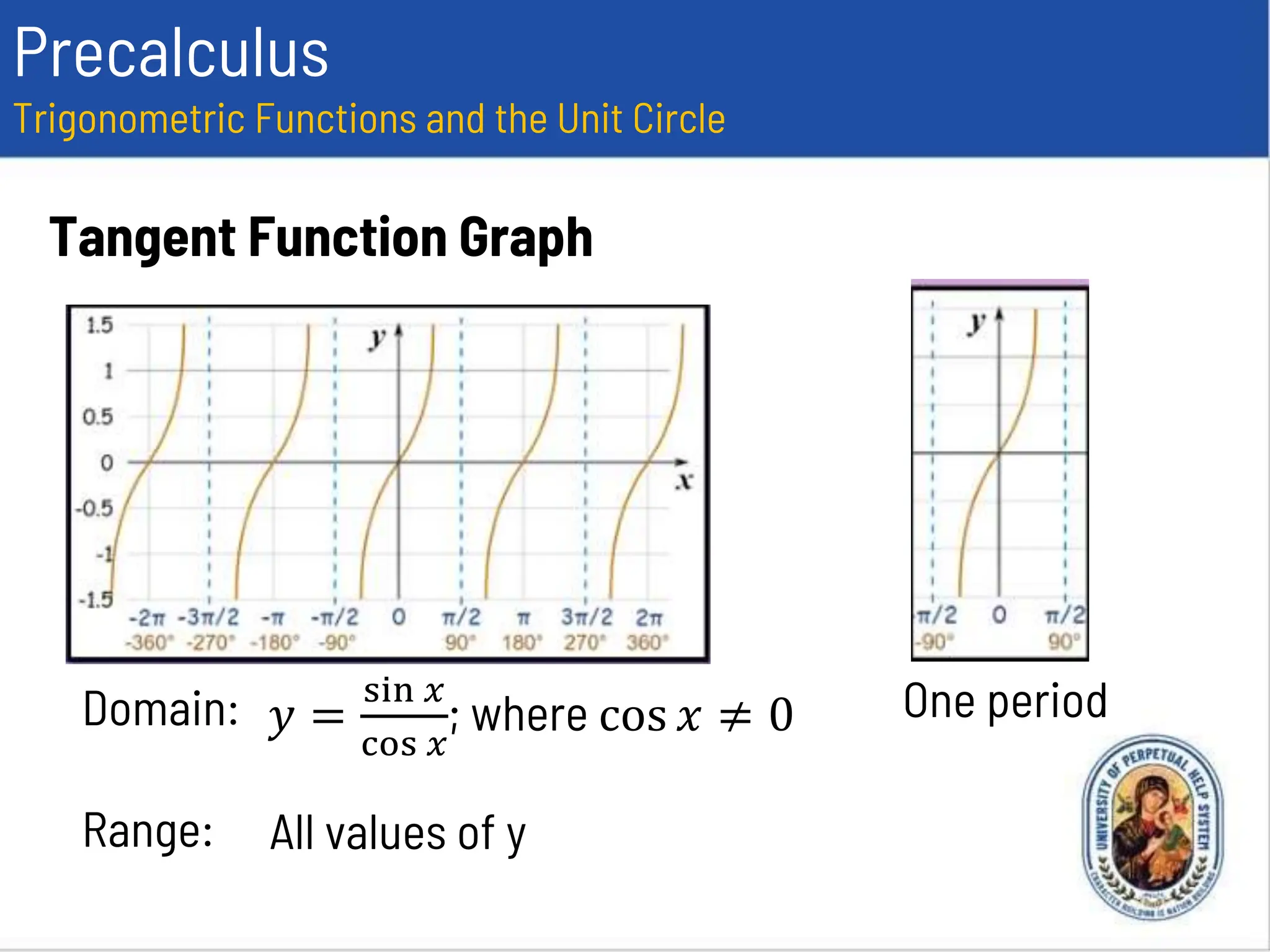
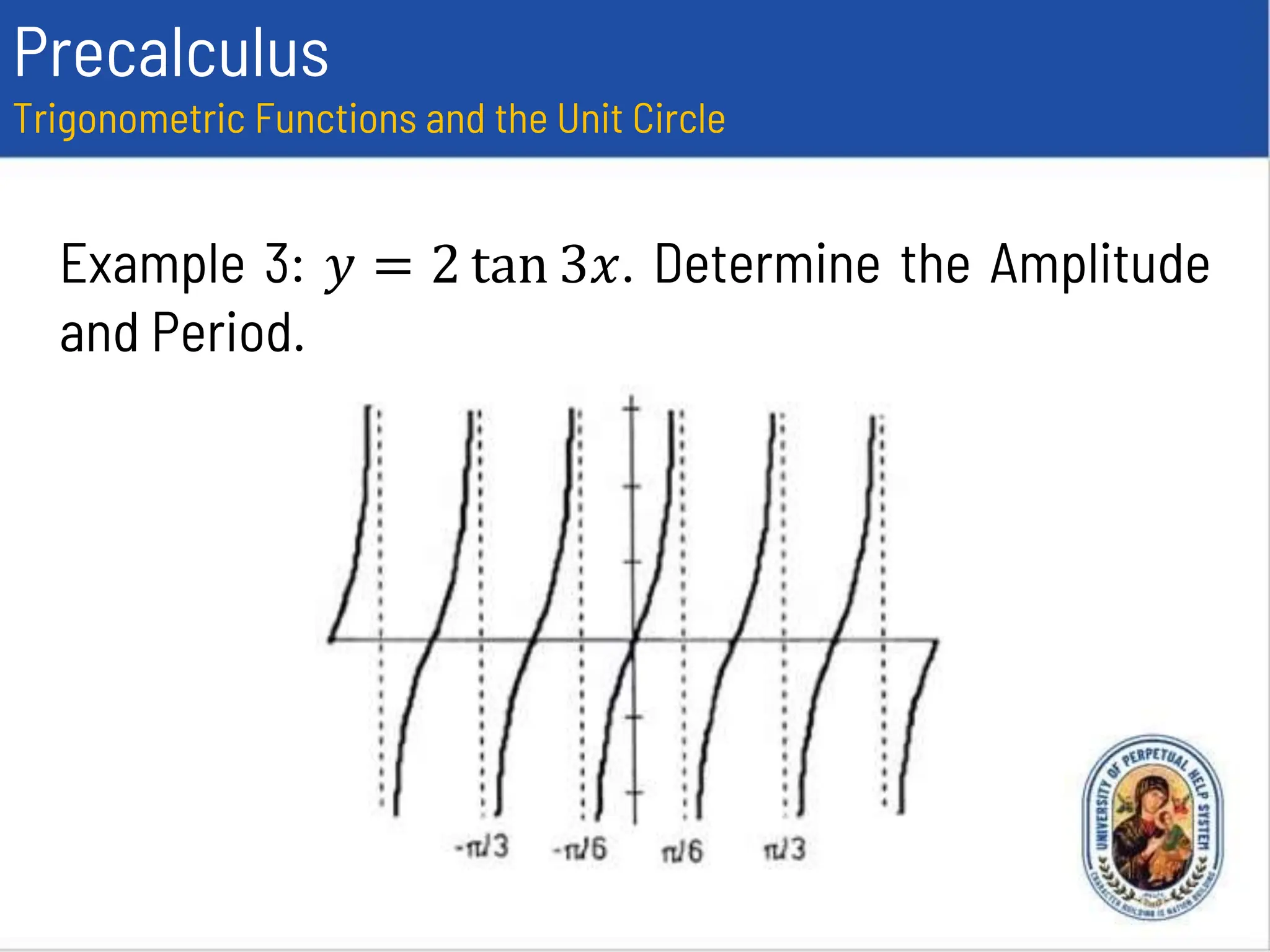
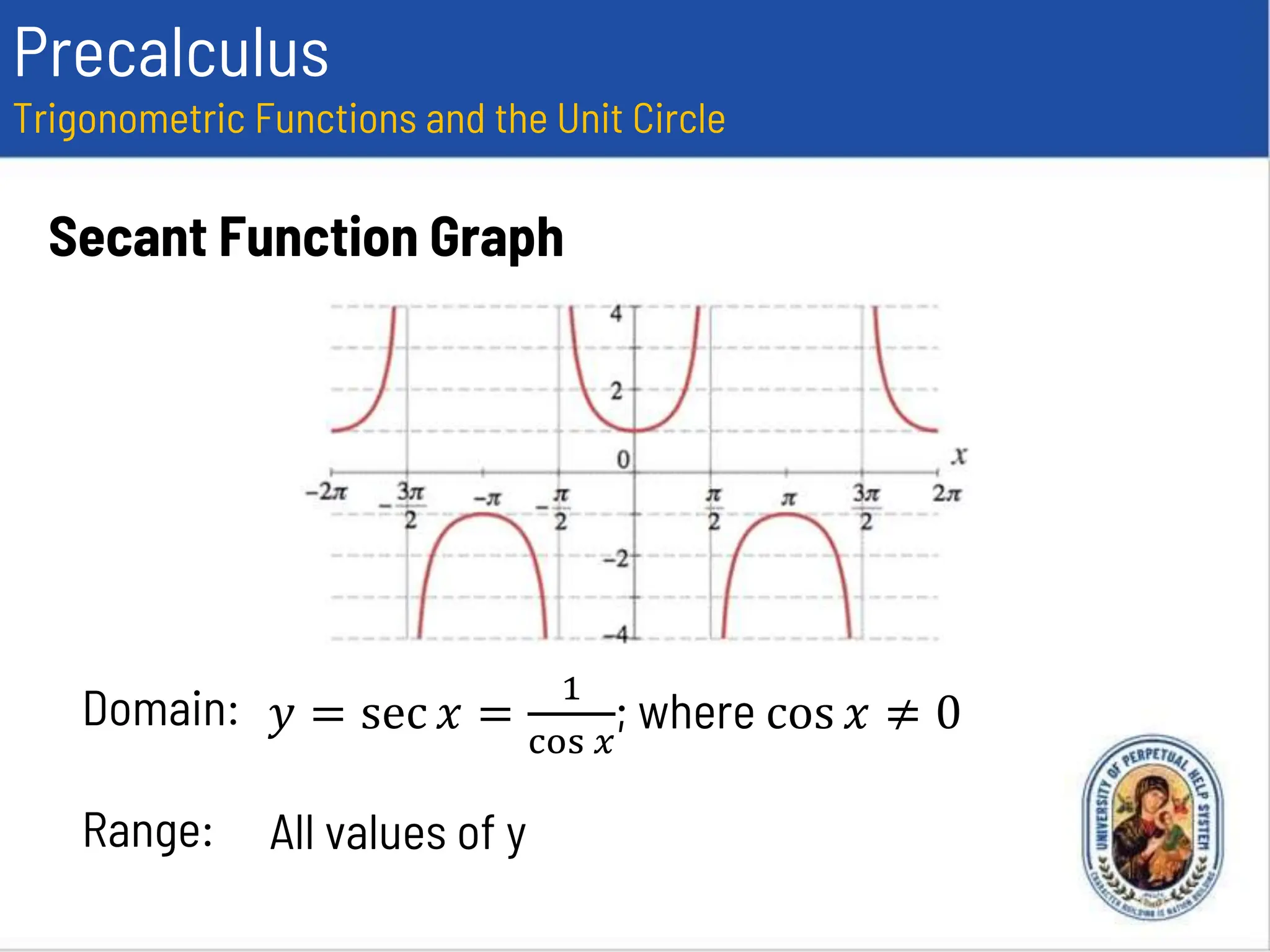
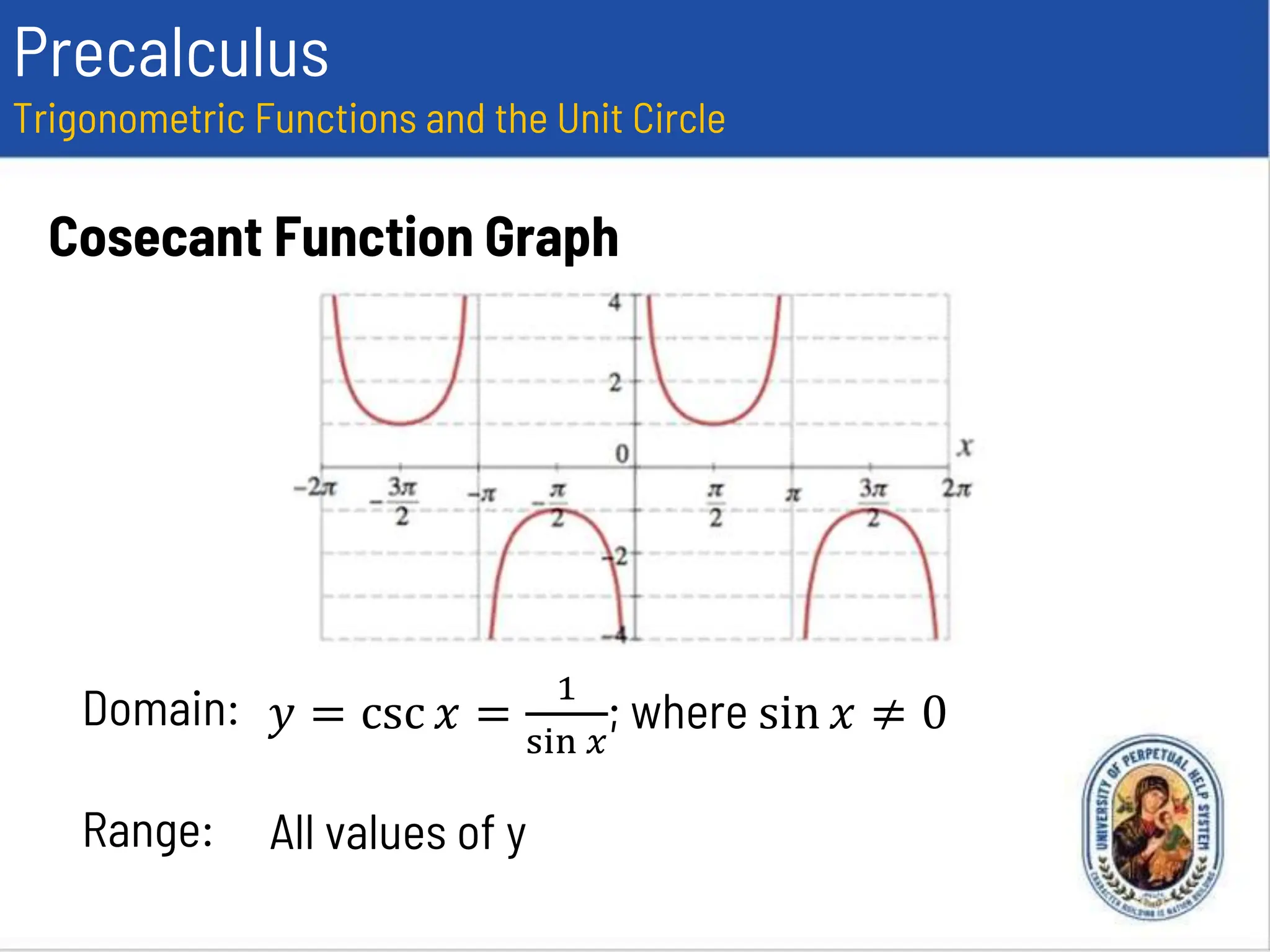
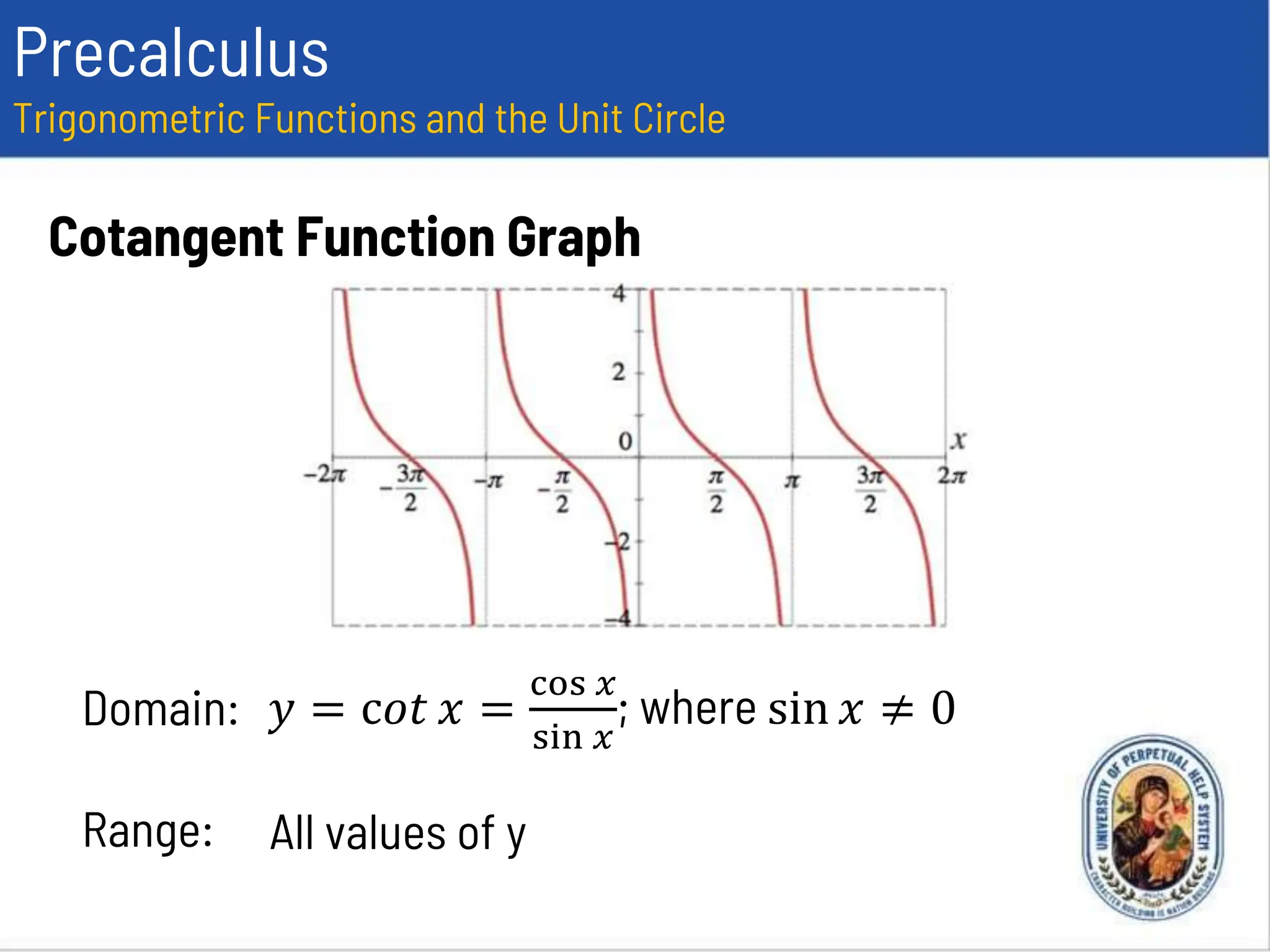
This document provides an overview of trigonometric functions using the unit circle approach. It defines the six trigonometric functions (sine, cosine, tangent, cotangent, secant, cosecant) using the unit circle. It discusses the domain, range, amplitude and period of the sine, cosine, tangent, secant, and cosecant functions. Examples are provided to determine the amplitude and period of specific trigonometric functions.

1. Lesson 10: The Trigonometric Functions:
The Unit Circle Approach
Precalculus
Unit 3: Trigonometric Functions

2. At the end of the lesson, the learner is expected
to:
 Use a unit circle to define trigonometric
functions of real numbers;
 Recognize the domain and range of
trigonometric functions.
Learning Objectives:
Precalculus
Trigonometric Functions and the Unit Circle

3. Precalculus
Trigonometric Functions and the Unit Circle

4. 1. What do you notice about the figure in
the previous slide?
2. Can you name some of trigonometric
functions?
Answer the following key questions:
Precalculus
Trigonometric Functions and the Unit Circle

5. Trigonometric Functions using Unit Circle
sin 𝜃 =
𝑦
1
= 𝑦
cos 𝜃 =
𝑥
1
= 𝑥
tan 𝜃 =
𝑦
𝑥
=
sin 𝜃
cos 𝜃
csc 𝜃 =
1
𝑦
=
1
sin 𝜃
sec 𝜃 =
1
𝑥
=
1
cos 𝜃
cot 𝜃 =
𝑥
𝑦
=
cos 𝜃
sin 𝜃
Precalculus
Trigonometric Functions and the Unit Circle

6. Precalculus
Trigonometric Functions and the Unit Circle
Special Angles in Trigonometric Functions

7. Examples
1.cos 90°
2.cos
𝜋
3
3.csc 180°
4.tan 45°
5.sec 270°
6. cot 0°
7. cos 330°
8. sin −
𝜋
4
9. sec −
3𝜋
4
10. tan 390°
Precalculus
Trigonometric Functions and the Unit Circle

8. Precalculus
Trigonometric Functions and the Unit Circle
Definitions
Amplitude- maximum ordinate (𝑦) value.
Period- length of the smallest domain
interval which corresponds to a complete
cycle of values of a function.

9. Sine Graph
Precalculus
Trigonometric Functions and the Unit Circle

10. Precalculus
Trigonometric Functions and the Unit Circle
−∞ < 𝑥 < +∞
Domain:
−1 ≤ 𝑦 ≤ 1
Range:
One period
Sine Function Graph

11. Precalculus
Trigonometric Functions and the Unit Circle
Example 1: 𝑦 = 3 sin
𝑥
2
. Determine the Amplitude
and Period.

12. Cosine Graph
Precalculus
Trigonometric Functions and the Unit Circle

13. Precalculus
Trigonometric Functions and the Unit Circle
−∞ < 𝑥 < +∞
Domain:
−1 ≤ 𝑦 ≤ 1
Range:
One period
Cosine Function Graph

14. Precalculus
Trigonometric Functions and the Unit Circle
Example 2: 𝑦 =
1
2
cos 2𝑥 . Determine the Amplitude
and Period.

15. Precalculus
Trigonometric Functions and the Unit Circle
Amplitude and Period
For the functions of the form:
𝒚 = 𝒂 𝒔𝒊𝒏 𝒃𝒙
𝒚 = 𝒂 𝐜𝐨𝐬 𝒃𝒙
Amplitude: 𝒂
Period: =
2𝜋
𝑏

16. Precalculus
Trigonometric Functions and the Unit Circle
Tangent Graph

17. Precalculus
Trigonometric Functions and the Unit Circle
𝑦 =
sin 𝑥
cos 𝑥
; where cos 𝑥 ≠ 0
Domain:
All values of y
Range:
One period
Tangent Function Graph

18. Precalculus
Trigonometric Functions and the Unit Circle
Amplitude and Period
For the function of the form: 𝒚 = 𝐭𝐚𝐧 𝒃𝒙
Amplitude: None, since there are no
maximum value for 𝑦.
Period: =
𝜋
𝑏

19. Precalculus
Trigonometric Functions and the Unit Circle
Example 3: 𝑦 = 2 tan 3𝑥. Determine the Amplitude
and Period.

20. Precalculus
Trigonometric Functions and the Unit Circle
𝑦 = sec 𝑥 =
1
cos 𝑥
; where cos 𝑥 ≠ 0
Domain:
All values of y
Range:
Secant Function Graph

21. Precalculus
Trigonometric Functions and the Unit Circle
𝑦 = csc 𝑥 =
1
sin 𝑥
; where sin 𝑥 ≠ 0
Domain:
All values of y
Range:
Cosecant Function Graph

22. Precalculus
Trigonometric Functions and the Unit Circle
𝑦 = c𝑜𝑡 𝑥 =
cos 𝑥
sin 𝑥
; where sin 𝑥 ≠ 0
Domain:
All values of y
Range:
Cotangent Function Graph

23. Reference
Bacani, J. et. Al. Precalculus (Teaching Guide for Senior
High School). Published by Commission on Higher
Education, 2016.
https://www.mathsisfun.com/