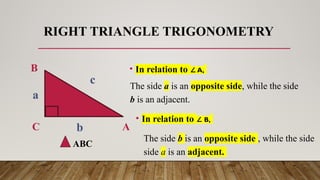
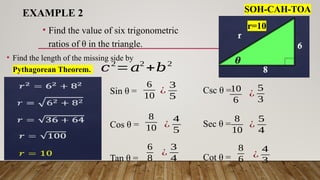
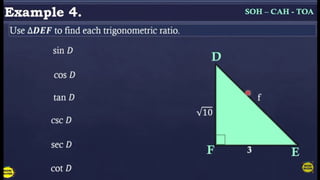
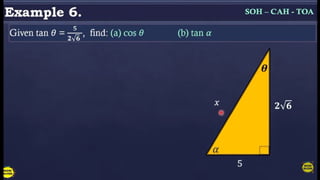
The document discusses the six trigonometric ratios: sine, cosine, tangent, cosecant, secant, and cotangent, which relate to the angles and sides of triangles. It primarily focuses on right triangle trigonometry, explaining how to identify sides as opposite, adjacent, and hypotenuse, and provides mnemonic devices for remembering the ratios. Additionally, it touches on the use of the Pythagorean theorem to find missing side lengths.

1. THE SIX TRIGONOMETRIC RATIOS
(SINE, COSINE, TANGENT, COSECANT, SECANT, COTANGENT)

2. TRIGONOMETRY
• It is the branch of mathematics that deals with the relation between
the sides and angles of a triangle.
• It is from the Greek words “trigon” trigon meaning triangle and
“metron means “measurement of triangles.
• It is a tool use for measuring distances that cannot be directly
measured.

3. RIGHT TRIANGLE TRIGONOMETRY
• It is often used to find the length of the side or the measure of an
acute angle of a right triangle.
A
B
C
a
b
c
• Hypotenuse is always the side opposite the right
angle, it is the longest side of a right triangle.
• The side opposite an angle is called an
opposite side, and the side which is also a
side of the angle is called an adjacent side.

4. RIGHT TRIANGLE TRIGONOMETRY
A
B
C
a
b
c
• In relation to A,
∠
The side a is an opposite side, while the side
b is an adjacent.
• In relation to B,
∠
The side b is an opposite side , while the side
side a is an adjacent.
ABC

5. THE SIX TRIGONOMETRIC RATIOS
opposite
• The three primary trigonometric ratios are sine, cosine and tangent
hypothenuse
adjacent
θ

6. THE SIX TRIGONOMETRIC RATIOS
opposite
• The three secondary trigonometric ratios are cosecant, secant and
cotangent.
hypothenuse
adjacent
θ

7. THE SIX TRIGONOMETRIC RATIOS
• SOH-CAH-TOA
• SOH-sin (opposite, hypothenuse)
• CAH-cos (adjacent, hypothenuse)
• TOA-tan (opposite, adjacent)
• CHO-SHA-CAO
• CHO-cos (hypothenuse, adjacent)
• SHA- sec (hypothenuse, adjacent)
• CAO-cot (adjacent, opposite)

8. • SOH-CAH-TOA
opposite
adjacent
hypothenuse
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
h h
𝑦𝑝𝑜𝑡 𝑒𝑛𝑢𝑠𝑒
3
5
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
h h
𝑦𝑝𝑜𝑡 𝑒𝑛𝑢𝑠𝑒
4
5
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
3
4
h h
𝑦𝑝𝑜𝑡 𝑒𝑛𝑢𝑠𝑒
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒
5
3
h h
𝑦𝑝𝑜𝑡 𝑒𝑛𝑢𝑠𝑒
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
5
4
𝑎𝑑𝑗𝑎𝑐𝑒𝑛𝑡
𝑜𝑝𝑝𝑜𝑠𝑖𝑡𝑒 4
3

10. • Find the value of six trigonometric
ratios of θ in the triangle.
• Find the length of the missing side by
Pythagorean Theorem. 𝑐2
=𝑎2
+𝑏2
EXAMPLE 2
r=10
SOH-CAH-TOA
Sin θ =
Cos θ =
Tan θ =
Csc θ =
Sec θ =
Cot θ =
6
10
¿
3
5
8
10 ¿
4
5
6
8
¿
3
4
¿
5
3
¿
5
4
¿
4
3
10
6
8
10
8
6