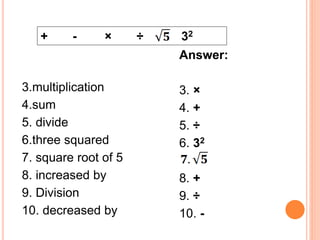
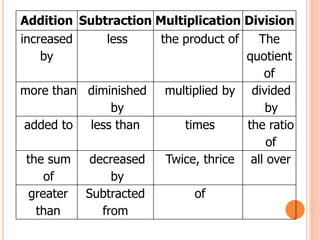
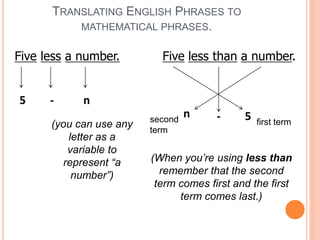
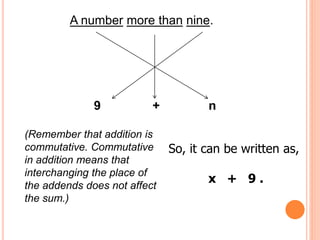
This document provides examples for translating between English phrases and mathematical expressions. It begins by outlining learning objectives around differentiating English phrases from mathematical symbols and translating between the two. Examples are then given for translating common terms like "sum," "multiplication," and others into mathematical symbols. Students practice translating phrases involving operations, variables, and order of operations. Key terms for translation are defined. Overall, the document aims to help students learn the relationship between verbal descriptions of mathematical concepts and their symbolic representations.

1. TRANSLATING ENGLISH
PHRASES TO MATHEMATICAL
PHRASES AND VICE VERSA
Prepared by:
Mae Ann Joy Matrido

2. At the end of the lesson, the students should
be able to: (M7AL-IIc-1)
a. differentiate English phrases from
mathematical symbols;
b. translate English phrase to mathematical
phrases and vice versa; and
c. appreciate the importance of using
symbols.

3. ACTIVITY 1
1.times
2.plus
+ - × ÷ 32
Choose appropriate symbol to use in the box
which corresponds to the following
words/phrases.
Answer:
1. ×
2. +

4. 3.multiplication
4.sum
5. divide
6.three squared
7. square root of 5
8. increased by
9. Division
10. decreased by
+ - × ÷ 32
Answer:
3. ×
4. +
5. ÷
6. 32
8. +
9. ÷
10. -

5. Activity 2: Find Me
Direction: Each envelope contains different
word/phrases and each group should look for the
phrases with the same meaning.
increased by
the quotient of
more than
less
the product of
diminished by
divided by
less than
added to
multiplied by
decreased by
times

6. English phrases are
composed of word or group of
words while mathematical
phrases are composed of
numbers/digit and symbols
such as the fundamental
operations, exponents, radical
signs, etc.

7. Some of the key words used in translating
English phrases to mathematical symbols.

8. Addition Subtraction Multiplication Division
increased
by
less the product of The
quotient
of
more than diminished
by
multiplied by divided
by
added to less than times the ratio
of
the sum
of
decreased
by
Twice, thrice all over
greater
than
Subtracted
from
of

9. TRANSLATING ENGLISH PHRASES TO
MATHEMATICAL PHRASES.
Five less a number. Five less than a number.
second
term
first term
(When you’re using less than
remember that the second
term comes first and the first
term comes last.)
(you can use any
letter as a
variable to
represent “a
number”)
5
n
- n
- 5

10. A number more than nine.
9 + n
(Remember that addition is
commutative. Commutative
in addition means that
interchanging the place of
the addends does not affect
the sum.)
So, it can be written as,
x + 9 .

11. A number increased by nine.
n + 9
It can be written as,
9 + x .

12. The product of ten and a number.
10 . y 10y
(Remember that
multiplication is also
commutative. Commutative
in multiplication means that
interchanging the factors
does not affect the product.)
So, it can be
written as,
y · 10 .

13. However, in multiplying a number and a
variable, always remember that number always
comes first thus, y · 10 is also 10y.

14. The quotient of six and a number.
6 ÷ m

15. Now it’s your turn. Translate the following into
mathematical phrase.
1. Twelve more than a number.
2. Ten less a number b.
3. Three multiplied to a
number.
4. Six less than a number w.
5. The quotient of seven and a
number.
Answer:
1.
2.
3.
4.
5.
+ 12
n
-
10 b
3n
w - 6
7 ÷ n

16. Six times the sum of two and a number.
6 . ( )
2 n
+
It can be simply written as 6(2+n) .

17. Twice a number plus seven.
2n + 7
(Twice means 2
times, so twice a
number means 2
times a number
thus, 2 ·n or
simply 2n.)

18. The sum of six and thrice a number plus five.
6 + ( )
3n + 5
(Thrice means 3
times, so thrice
a number means
3 times a
number thus, 3·n
or simply 3n.)

19. Now it’s your turn.
1.Five multiplied by the sum of
eight and a number.
2.Twice a number divided by four.
3.The difference of six and twice a
number plus three.
Answer
1.
2.
3.
5 ( )
+
8 m
2n ÷ 4
-
6 ( 2y )
+ 3

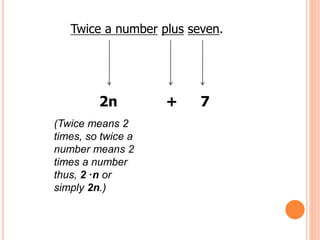
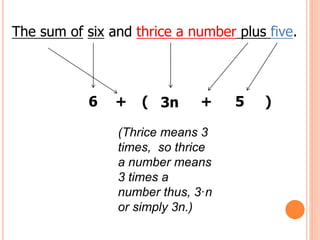
20. Let’s do it!
A. Direction: Choose the correct answer of the
following in the parenthesis.
1.The product of 6 and a number plus five.
(6x + 7 , 6 + 7x )
2. Ten more than a number. ( n + 10 , 10n )
3. A number subtracted from twelve. ( m – 12, 12
– m )
4. Fifteen divided by the difference of eight and
three. ( 15 ÷ [8 – 3] , 15 ÷ [3 – 8] ).

21. 5.4 (m ÷ 9) ( Four times a number divided by
nine, four times the quotient of a number and
nine)
6.The product of five and a number added to
three. ( 5n - 3 , 3 + 5n )
7. 6 + 2n (six decreased by twice a number, six
increased by twice a number )
8. 4x – 8. (eight less than the product of four
and a number, eight less the product of four
and a number )

22. B.
1. Ester is 5 years older than Ric . Let r represent
the age of Ric. Write a mathematical symbol
expression of
Ester’s age.
Answer: r + 5
2. Renze has dimes and quarters in his pocket. The
number of dimes is 5 less than four times the
number of quarters. Let q represent the number of
quarters. Write a mathematical expression of
dimes.
Answer: 4q - 5

23. Do it Alone!
A. Translate the word problem into mathematical
expression.
1. The length of a rectangle is 5 inches less than
the width. Let w represent the width of the
rectangle. Write an expression for the length of
the rectangle.

24. B. Translate the following mathematical
expressions into verbal phrases.
1. (x + 10) 5
2. 10 – n
3. 5r 6
4. 3d + 5
5. 6 + 2n

25. THANK YOU!