1. 1
Åðºíõèé õèìèéí ëåêö¿¿ä
Ëåêö ¹4
1. Àòîìûí íàðèéí íèéëìýë á¿òýö
2. Àòîìûí ýëåêòðîíò á¿òýö.
Àòîìûí ýëåêòðîíò á¿òöèéã òàéëáàðëàõ
êâàíò ìåõàíèêèéí îíîë
• 19 -ð çóóíû ýöýñ. Ôèçèêèéí øèíæëýõ óõààíû íýýëò¿¿ä
• Àòîìûí á¿òöèéí çàãâàðóóä
• Àòîìûí á¿òöèéí îíîëóóä
• Àòîìûí ýëåêòðîíò á¿òýö áà êâàíò ìåõàíèê
• Óñòºðºã÷èéí àòîìä áè÷ñýí Øðåäèíãåðèéí òýãøèòãýë,
ò¿¿íèé øèéäèéí õàðèó
• Êâàíòûí òîî (n, l, ml) –íóóä, òýäãýýðèéí àâàõ óòãà
• Àòîìûí îðáèòàëü òºëºâ áàéäëóóä

2. 2
1. Àòîìûí íàðèéí íèéëìýë á¿òýö
19-ð çóóíû ýöýñ õ¿ðòýë àòîì íü öààø ¿ë õóâààãäàõ áîäèñûã
á¿ðä¿¿ëýã÷ æèæèã õýñýã ãýæ ¿çýæ áàéâ.
(Atomos = º÷¿¿õýí áàãà õóâààãäàøã¿é ãýñýí ãðåê ¿ã)
Êàòîäûí òóÿà áóþó ýëåêòðîíûã (e-) -ûã 1897 îíä Àíãëèéí ôèçèê÷
Joseph Tomson /1856-1940/ íýýæ, õàñàõ öýíýãò æèæèã õýñãèéí óðñãàë áîëîõûã
òîãòîîæ ò¿¿íèéã ýëåêòðîí ãýæ íýðëýñýí.
Àíîäûí òóÿà = ñóâãèéí òóÿà áóþó протон (protos) -ûã 1886 îíä Ãåðìàíû ôèçèê÷
Goldstein íýýñýí áºãººä óëìààð Â.Âin, J.J.Thomson íàð ñóäàëæ íýìýõ öýíýãò
æèæèã õýñãèéí óðñãàë áîëîõûã òîãòîîñîí
Ñààðìàã æèæèã õýñýã íåéòðîí (neutrons) -ûã 1932 îíä Àíãëèéí ôèçèê÷
James Chadwich íýýæ, ò¿¿íèé ìàññ íü ïðîòîíû ìàññòàé îéðîëöîî áîëîõûã
àæèãëàñàí.

3. 3
Òýìäýãëýý Цýíýã Õàðüöàíãóé àòîì
ìàññ /relative/
Үíýìëýõ¿é àòîì ìàññ /actual/
e- ýëåêòðîí 1- 1/1840
(ïðîòîíû ìàññ)
9.11 · 10-28
ð+ ïðîòîí 1+ 1 1.67 · 10-24
n 0 íåéòðîí 0 1 1.67 · 10-24
• Ãåðìàíû ýðäýìòýí À.Áåêêåðåëè öºìèéí öàöðàã èäýâõò øèíæ ÷àíàðûã
1896 îíä èëð¿¿ëñýí
• Ôðàíöûí ýðäýìòýí Ìàðè áà Ïepu Êþðè íàð öàöðàã èäâýõò ÷àíàð àòîìûí
öºìèéí çàäðàëûí á¿òýýãäõ¿¿í áîëîõûã òîãòîîñîí (àëüôà, áåòòà, ãàììà òóÿà)
ï pî òî í
Þ Þ Þ ®
aтoмí óêëî íкварк
í åéòpî í
10- 10- 10- 10-
8 12 13 16
ñì ñì ñì ñì

4. 4

5. 5
Àòîìûí á¿òöèéí çàãâàðóóä
1. 1904 îíä Àíãëèéí ôèçèê÷ Òîìñîí áºìáºðöºã çàãâàð ãàðãàñàí e-,
Ẻìñ ìåòàëë ÿëòàñ äóíäóóð íýâòðýõýäýý õàðèëöàí àäèëã¿é ñàðíèäàã шинжèéã
¿íäýñëýñýí. 1Àо äèàìåòðòýé ïðîòîí á¿õ ýçýëõ¿¿íýýð æèãä òàðõñàí áºìáºðöºã,
ò¿¿íèé ìàíäàë äýýã¿¿ð ýëåêòðîí õºâæ áàéíà.Ýëåêòðîíû õýëáýëçëýýð
îðîí çàéä öàõèëãààí ñîðîíçîí äîëãèîí öàöàðíà ãýæ ¿çñýí.
2. 1904 îíä ßïîíû ýðäýìòýí Õ.Íàãàîêî ñàí÷èð ãàðèãàí çàãâàð áóþó ýëåêòðîíû
á¿ðõ¿¿ëò çàãâàðûã á¿òýýñýí.
3. 1907 îíä Àíãëèéí ôèçèê÷ Ðåçîðôîðä àëüôà òóÿàíû ñàðèíàëûí òóðøèëò
õèéæ, 1911 îíä ãàðèãàí çàãâàð äýâø¿¿ëñýí.
0.0001ñì Pt ÿëòàñ ≈3ìÿíãàí àòîì àãóóëíà ãýæ ¿çñýí
3. 1920 îíä Àòîìûí á¿òöèéí õàãàñ êâàíòûí îíîëûã Äàíèéí ýðäýìòýí Í.Áîð
áîëîâñðóóëæ, àòîìûí ýëåêòðîí äàâõðààò çàãâàðûã ãàðãàñíààð Ðåçîðôîðäûí
äóòàãäëûã çàññàí.
4. 1920 èîä îíîîñ êâàíò ìåõàíèêèéí çàãâàð ãàðñàí. Ýíý çàãâàð ¸ñîîð öºìèéí
¿éë÷ëýëèéí îðîí çàéä ýëåêòðîí îðøèõ ìàãàäëàë 90% -ûã àãóóëñàí ýçýëõ¿¿íä
ýëåêòðîí òîäîðõîéëîãäîíî ãýæ ¿çñýí.

6. 6
Òîìñîíû
çàãâàð
Õ. Íàãàîêàûí
çàãâàð
Í.Áîðûí
çàãâàð
Peçåðôîðäûí
çàãâàð
Êâàíò ìåõàíèêèéí
çàãâàð
Орбиталын энегийн ихсэлт

7. 7
Òîìñîí òóðøëàãà
Ðåçåðôîðäûí òóðøëàãà
~3 ìÿíãàí àòîì àãóóëàõ 0.0001 ñì çóçààíòàé öàãààí àëòàí (Pt) ÿëòñûã a–Ẻ캺ð áºìáºãäсºí
20000 õàçàéëòààñ çºâõºí íýã íàçàéëò 90î –ûí õàçàéëò (ýðãýí îéñîí) –ûã ¿ç¿¿ëæ áàéæýý.

8. 8
 Ðåíòãåí ñïåêòð, Ìîçëèéí õóóëü.
- Ðåíòãåí òóÿà íü êàòîäààñ ãàð÷, àíòèêàòîä äýýð òóñàõ ¿åä /Õóðä = 0 ¿åä/ ¿¿ñíý.
- Ðåíòãåí ñïåêòð á¿ðèéí á¿ëýã øóãàìûã (K.L.M....) ãýæ òýìäýãëýíý
íýã á¿ëýã äîòðîî α, β, γ, δ ãýõ ìýò ñàëààëíà.
- Õèìèéí ýëåìåíò á¿ð íü ººðèéí òîäîðõîéëîã÷ ãîë ñïåêòð øóãàìûã ãàðãàäàã. Ðåíòãåí
ñïåòðèéí øóãàìààð íü òýð ýëåìåíòèéã òàíèíà.
- 1912 îíä àíòèêàòîäîîð ÿíç á¿ðèéí ýëåìåíòèéã õèéæ òóðøèõ ÿâöäàà ðåíòãåí ñïåêòðèéí
äîëãèîíû óðò, äîëãèîíû òîî (ν) íü ýëåìåíòèéí äýñ äóãààðòàé øóãàìàí õàìààðàëòàéã
òîãòîîñîí.
N- äýñ äóãààð
à- á¿ëýã øóãàìûí øóãàì á¿ðò òîõèðîõ òîãòìîë òîî.
b- á¿ëýã øóãàì á¿ðò òîõèðîõ òîãòìîë òîî.
R- Ðèäáåðãèéí òîãòìîë /3.2869·10-14ãö/
N ≈ Zöºì ãýæ áàòàëñàí.
= 1 = a(N - b)
l
n
N = n
R
Ýíý õóóëü: à) ¿åëýõ ñèñòåìä øèíý òîäîðõîéëîëò ºãñºí
á) ¯åëýõ ñèñòåìä ýëåìåíòèéí ýçëýõ áàéðûã íàéäâàðòàé òîãòîîõ áîëîìæ
îëãîñîí Ììàññûí òîî= MP + Mn
Èçîòîï /èæèë áàéðò/ - öºìèéí öýíýã èæèë, àòîì ìàññààðàà ººð.
Z=84-92 –ð ýëåìåíò áàéãàëüä áàéäàã ÷ òîãòâîðòîé èçîòîïã¿é. Z>93 çîõèîìîëîîð ãàðãàí
àâäàã, öàöðàã èäâýõò ÷àíàð ¿ç¿¿ëíý. ð, n – íû òîî íü 2, 8, 14, 20, 28, 50, 82 áîë øèäýò
öºì ãýíý.(øèäýò òîî)
Èçîáàð /èæèë ìàññòàé/ - öºìèéí öýíýã ººð ÷ , ìàññ íü èæèë.
Èçîòîí /èæèë äàðààëàëòàé/ - öºìèéí öýíýãýý𠺺ð, íåéòðîíû òîî èæèë .

9. 9
Ðåíòãåí ñïåêòð ¿¿ñýõ ÿâö

10. 10
H
Hg

11. 11
1. Н. Áîðûí õàãàñ êâàíòûí îíîë
Онол дэвшигдэх үндэслэл:
Àòîìûí ýëåêòðîíò á¿òöèéí ãàðèãàí çàãâàð ñîíãîäîã öàõèëãààí
äèíàìèêèéí ñóðãààëòàé õî¸ð ãàçàð çºð÷èëääºã.
• Òàñðàëòã¿é õºäëºã÷ e- òàñðàëòã¿é ýíåðãè àëäàж ààæèì óñòàíà.
Гýòýë àòîì òîãòâîðòîé оршдог.
• Òàñðàëòã¿é èõ õóðäòàé õºäëºã÷ áèåòèéí ñïåêòð íèë áóþó
¿ðãýëæèëñýí áàéõ ¸ñòîé.
Ãýòýë àòîìûí ñïåêòð òàñðàëòòàé áàéäàã.
1913 îíä Äàíèéí ýðäýìòýí Í.Áîð уñòºðºã÷èéí àòîìûí á¿òöèéã çàãâàð
áîëãîí “õàãàñ êâàíòûí îíîë” -îî ïîñòóëàò áàéäëààð äýâø¿¿ëэн атомын
шинж чанарыг тайлбарласан.

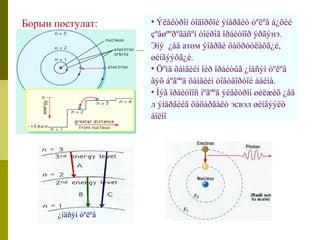
12. • Ýëåêòðîí òîäîðõîé ýíåðãèò òºëºâ á¿õèé
çºâøººðºãäñºí òîéðîã îðáèòîîð ýðãýнэ.
Эíý ¿åä атом ýíåðãè öàöðóóëàõã¿é,
øèíãýýõã¿é.
• Öºìä õàìãèéí îéð îðáèòûã ¿íäñýí òºëºâ
ãýõ áºãººä õàìãèéí òîãòâîðòîé áàéíà.
• Íýã îðáèòîîñ íºãººä ýëåêòðîí øèëæèõ ¿åä
л ýíåðãèéã öàöàðãàëò эсвэл øèíãýýëò
áîëíî
Борын постулат:
¿íäñýí òºëºâ

13. ò v e
2
2
r
e
1). n– ýëåêòðîíû øóãàìàí õóðä ãýâýë ýëåêòðîíû òºâººñ çóãàòàõ õ¿÷ íü òºâä òýì¿¿ëýõ õ¿÷ -òýé
òýíöýõ ¿åä òîéðîã îðáèòûí õºäºë㺺í òîãòâîðòîé áàéíà.
r
2 2
ò v e = Þ =
2
mv e
 
e
r
r
2). Ýëåêòðîíû íèéò ýíåðãè íü ò¿¿íèé ïîòåíöèàë áà êèíåòèê ýíåðãèéí íèéëáýðòýé òýíö¿¿ áàéíà.
2
2
r
E E E mv e Ê ï = + = -
2
2 2

r
H-èéí èîíæèëòèéí ýíåðãè íü 13.6 ýâ.
(2)
(3)
2 2 2 2 2 2 2
e e
= - = - = - 2
= -
e
r
2 2
e
m v e
r
2 2

r
e
r
r
3). Ýëåêòðîíû õºäºë㺺íò òîîíû ìîìåíò íü meve r ÿìàãò òàñðàëòòàé , á¿õýë = “êâàíò” óòãààð ÿëãàãäàíà.
ò v r n h x m ì
v = nийнhутгыг m v = дeорлуулбал - m n h =
e
p m r r p m r r
Áîðûí ðàäèóñ
2
(1)
r = n h =
n a
p m e
ао – тогтмол тоо
n = 2, 3, 4 ... – байх энергит төлөвийг ºäººãäñºí буюу ñýðñýí òºëºâ ãýíý.
n -èéã ãîë êâàíòûí òîî гэнэ. Аòîì äàõü ýëåêòðîíû ýíåðãèò òºëºâ áàéäëã òîäîðõîéëîõ áºãººä атомын
ñïåêòð шугам êâàíòëàгдах ¿íäýñ áîëäîã.
n = 1 2 3 4 5 6 7
K L M N O P Q 13
E e
íèéò
/ . . /
e e 2
p
=
2 2 2 2
2
2 2 2 . . ... .. ,
2 4
e
e
e e
0
0 n =1r = 0.53A
2 0
2 0 r = r n = 2.12A
2
o r = a n
2 2
2
4 2 2 o
e

14. 1. Ãýðëèéí ñïåêòðèéí ìºí ÷àíàðûã
òàéëñàí. 5-20 ý ýíåðãè ºãºõºä,
Ëàéìàí - óëüòðà ÿãààí,
Áàéëìàð - ¿çýãäýõ ãýðýë,
Ïàéøèí - èíôðà óëààí òóÿàíû ñïåêòð
Атомын спектрын íýã бүлэг шугамûí äîòîðõ
ñïåêð øóãàìûí çàéí èõñýëò.
ΔÅ2 »ΔÅ3 >ΔÅ4 ~ ΔÅ5 » ΔÅ6»ΔÅ7
14
Борын îíîëûí òàéëáàð:
¿çýãäýõ ãýðýë
Óëüòðà ÿãààí òóÿà Èíôðà óëààí òóÿà

15. 2. Ðåíòãåí ñïåêòðèéí ìºí ÷àíàðûã òàéëáàðëàñàí. Àòîìûí
äîòîîä äàâõðààíààñ ýëåêòðîí ñóãàëàí ò¿¿íèé áàéðûã
õàìãèéí îéð äàâõðны ýëåêòðîí эзэмших үед рентген
туяа цацарна
• Íýã ¿åèéí ýëåìåíòèéí ðåíòãåí ñïåêòðèéí á¿ëýã øóãàì ººð
¿åèéíõýýñ ýðñ ÿëãààòàé байна. Электрон äàâõðààны
тоо ººðчлөгдөхөд спектрийн бүлэг шугам
өөрчлөгдөнө.
2 2 2 2 2 1
ö çè
÷ø
4 2
e m
e e m
E e e e
íèéò
= - = - = - = æ 2 2
2 2 2
2
4
hR
2 n h
n h
n
r
p p
-1
é ù
1 1 109677.576 cm ni nf
E E hv R R
- = = ê - ú =
2 2
n n
êë f i
úû


16. Áîðûí îíîëûã õºãæ¿¿ëñýí íü:
Ñïåêòð àíàëèçûí áàãàæ óëàì áîëîâñðîíãóé áîëîõûí õèðýýð ñïåêòðèéí íýã á¿ëýã øóãàì äîòðîî íàðèéí
ñàëààëäàã áîëîõûã òîãòîîñîí. 1 ñïåêòð øóãàì õýñýã øóãàìààñ òîãòäîã. Ýíýõ¿¿ ç¿é òîãòëûã 1916 îíä
Ãåðìàíû ôèçèê÷ Çîììåðôåëüä àòîì öºìºº òîéðîí ýðãýõýäýý áºìáºðöºã çàìààð òîéðîõîîñ ãàäíà ýëëèïñ çàìààð
ýðãýæ áîëíî ãýæ ¿çñýí.
= 2
b r
0 r = bn 2
0.25
1
a R
0 R = a ´n 0
r
2
2
n
=1 = 0.7
= 0.5
=
R
1
1
1
n R
=
r - бага радиус болон R- их радиусûí õóâüä ðàäèóñ âåêòîð, ýðãýëòèéí ºíöºã ººð тул хоёр ëåêòðîí ººð
ºөөр õºäºë㺺íò òîîíû ìîìåíòèéí óòãà àâíà. Нýã ýíåðãèéí êâàíò òîî (n)-íû óòãàíä орших ýºð êâàíò óòãààð
èëýðõèëýãäýæ áîëíî. Ýðãýëòèéí îðáèòàëûí õýëáýðýýñ õàìààðàí ÿëãàãäàõ êâàíò óòãûã “l “ ãýæ
òýìäýãëýñýí.
l = 0. 1. 2....(n-1) á¿õýë òîîí óòãà àâíà. Оðáèòàë êâàíòûí òîî ãýíý. Мөн орбиталын энергит утгыг
илэрхийлнэ. Сïåêòð øóãàìûí òºðõ çààñàí àíãëè íýðíèé
ýõíèé ¿ñãýýð s, p, d, f ãýõ ìýòýýð
íýðëýõ
áîëñîí. Áîäèò àòîìûí îðáèòàëûí õýëáýð
ä¿ðñòýé õîëáîîã¿é
=
=
1 2 3
0 0 1 0 1 2
s s , p s , p ,
d
n
l
Эíýõ¿¿ ñóäàëãàà,
Зºâõºí H -èéí àòîìûí ñïåêòð ç¿é òîãòîë, á¿òöèéã òàéëáàðëàñàí.
Ãàäíû ñîðîíçîí îðíû íºëººãººð ñïåêòð øуãàì ñàëààëàõ ¿çýãäëèéã òàéëáàðëàñàí 16

17. 1920 –èîä îíä Ôðàíöûí Ëóé Äå – Áðîéë, Ãåðìàíû Ãåéçåíáåðã, Àâñòðèéí Ý. Øðåäèíãåð,
Äàíèéí Í.Áîð, Àíãëèéí Äèðàê Ï.À., Ôîê .Â.À. íàðûí ýðäýìòýäýýñ àòîì, ýëåêòðîí,
ìîëåêóëü çýðýã æèæèã áèåòèéí õºäºë㺺í, ìºí ÷àíàðûã òàéëáàðëàõ òóñãàé àðãà áîëñîí
äîëãèîíû ìåõàíèêèéí øèíý ñàëáàðûã áèé áîëãîñîí /Ýíý íü ö.ñ.ä –íû òàðõàëòûí õóóëü ç¿é
áîëñîí êâàíò ìåõàíèêèéí ¿çýë ñàíààã ººðòºº àãóóëñàí байñàí./
Ñîíãîäîã ìåõàíèêò áèåòèéí òºðõèéã ò¿¿íèé õºäºë㺺íèé òðàåêòîð = óë ìºðººð èëýðõèéëäýã
áîë,
 Дîëãèîíû ìåõàíèêò äîëãèîëîã áîëîí Ẻìëºã хоёрмол øèíæ ÷àíàðтай áè÷èë
áèåòèéí òºðõèéã ò¿¿íèé îðøèõóéí ìàãàäëàëààð èëýðõèéëäýã.
 Áè÷èë áèåòèéí õî¸ðäìîë øèíæ ÷àíàð( äóàëèçì)-ыг òîäîðõîéã¿éí õàðüöàà,
õàðèëöàí íºõºõ¿éí çàð÷èì, ìàãàäëàë, ýëåêòðîí ¿¿ë, äîëãèîíû ôóíêö çýðýã êâàíò
ìåõàíèêèéí ¿íäñýí çàð÷èì, óõàãäàõóóíóóä äýýð ¿íäýñëýí тайлбарлана.
17
Ýëåêòðîíû äîëãèîëîã òºðõ, äîëãèîíû ìåõàíèê.
Àòîìûí электронт бүтцийн êâàíò ìåõàíèêèéí çàãâàð.

18. Дэлгэрүүлэн унших ñýäýâ
 1900 îíä Ì.Ïëàíê àòîìààñ öàöðàõ ãýðëèéí ýíåðãè áàãöààð/êâàíòààð/öàöàðäàã áºãººä öàöàðãàëòûí
ýíåðãè íü ãýðëèéí äàâòàìæààñ õàìààðíà ãýæ ¿çñýí
 - 1905 îíä Ýéíøòåéí áèåòèéí ìàññûí ººð÷ëºëòòýé ýíåðãè õîëáîîòîéã òîãòîîñîí.
 1924 îíä Ëóé-Äå-Áðîéë äîëãèîëîã øèíæ ÷àíàð çºâõºí ãýðýëä òºäèéã¿é áóñàä á¿õ /ýãýë/ áè÷èë
áèåòýä õàìààòàéã òîãòîîñîí. Ëóé-Äå-Áðîéëûí äîëãèîí Áîðûí äýâø¿¿ëñýí õºäºë㺺íò òîîíû ìîìåíòèéí
êâàíòëàãäàõ òóõàé ïîñòóëàòûã îíîëûí õóâüä áàòàëñàí.
 1927 îíä Äåâèññîí, Äæåìåð íàð íèêåëèéí ìîíîêðèñòàëèéí äóíäóóð ýëåêòðîíûã òóñãàõàä äèôðàêöèéí
øèíæ ÷àíàð ¿ç¿¿ëæ áàéñàí /òàëñò òîðûí äóíäóóð ãýðýë íýâòðýõýä ¿ç¿¿ëäýã äèôðàêöòàé àäèë/
Ýëåêòðîíû äîëãèîíû óðò òàëñò òîðûí çàéòàé õàðãàëçàæ áàéõûã ¿íäýñëýñýí.
 1925 îíä Ãåéçåíáåðã ýëåêòðîíû äîëãèîëîã áîëîí Ẻìëºã øèíæ ÷àíàðûí õàðüöààã ººðèéí
áîëîâñðóóëñàí òîäîðõîéã¿éí çàð÷èìààð òàéëáàðëàñàí. Áîäîõóéí ñîðèë õèéñýí.
Ôîòîíû ýíåðãè (E) áàãà ¿åä áàéðàà áàãà ñîëèíî. Ýíý ¿åä áàéðëàëûã òîäîðõîéëæ áîëíî.
Õóðä (υ) èõòýé ôîòîíòîé ìºðãºëäºõ òºäèé õóãàöààíä ÿâæ ºíãºðñºí çàì èëýðíý.
- õºäºë㺺íã¿é áèåòèéí õóðäûã òîäîðõîéëîõ áîëîìæã¿é,
- õóðä èõòýé áèåòèéí áàéðëàëûã òîäîðõîéëîõ áîëîìæã¿é.
Òîäîðõîéã¿éí íýãýí çóðâàñò ýëåêòðîí õºäëºõ áºãººä ýëåêòðîíû áàéð, õóðäûí ¿ðæâýð
áàéíà.
DX ×DP ³ h
 Í.Áîð õàðèëöàí íºõºõ¿éí çàð÷ìûã òîìú¸îëñîí. Õî¸ðäìîë øèíæ ÷àíàð áèå áèåý ¿ã¿éñãýäýã ÷ øèíæ
÷àíàð òîäîðõîéëîõîä áèå áèåý íºõºæ ºãäºã.
p 4

19. Õî¸ðäìîë øèíæ ÷àíàðòàé ýëåêòðîíû òºðõ öºìèéí ¿éë÷ëýëèéí îðîíä èëðýõ
ìàãàäëàëààð òîäîðõîëîãäîíî. Ýíýõ¿¿ ìàãàäëàëûí îðîí çàéä ýëåêòðîí äîëãèîëîã òºðõòýé áàéõ
áºãººä ò¿¿íèé õºäºë㺺íèé òºðõèéã äîëãèîíû òýãøèòãýëýýð òîäîðõîéëíî
Àòîì äàõü ýëåêòðîíû òºðõèéã ôóíêö áàéäëààð áè÷èõäýý òîãòîëöîîíû ýíåðãèéã ãàìåëüòîíû
Hy = Ey
ö
÷ ÷ø
æ
ò
Ñ + - = Ñ = ¶ Y 2
ç çè
+ ¶ Y
¶
+ ¶ Y
¶
¶
2
2
2
2
2
e y 2
y
2 ( ) 0
2
8
x y z
E U
h
y n
p
y
îïåðàòîð H – ð èëýðõèéëíý.
H –yíü -ôóíêöèéí ¿éëäëèéí äàðààëëûã òîäîðõîéëíî
y àòîìûí îðîí çàéí ÿíç á¿ðèéí öýãò òîäîðõîé òãà àâäàã
ýëåêòðîíû òºðõèéã òîäîðõîéëîã÷ õýìæèãäõ¿¿í
y =y (x, y, z) äîëãèîíû ôóíêöèéí ìàòåìàòèê áè÷èãëýë
Öºì ýëåêòðîíòîé õàðèëöàí ¿éë÷ëýõýä äîëãèîëîã òºðõ èëðýõã¿é ãýæ ¿çýí çºâõºí
ýëåêòðîíä äîëãèîíû òýãøèòãýë áè÷íý.1927 îíä Øðåäèíãåð óñòºðºã÷èéí àòîìûí
ýëåêòðîíä äîëãèîíû òýãøèòãýëèã áè÷ñýí
Ñ - íàáëà , Y - ôóíêöèéí õ,ó,z-òýíõëýãýýñ àâñàí 2-ð ýðýìáèéí óëàìæëàë

20. Y ôóíêöèéí ôèçèê óòãà:
Y 2 íü àòîìûí îðîí çàéí òóõàéí öýãò áàéõ ýëåêòðîíû ìàãàäëàëûã èëýðõèéëíý.
Y 2 dV – ýëåìåíòàð ýçýëõ¿¿íä òîäîðõîéëîãäîõ ýëåêòðîíû ìàãàäëàëûã çààíà.
Ìàãàäëàëûã ýëåêòðîí ¿¿ë áàéäëààð ä¿ðñëýí, ýëåêòðîíû 90% -èéí ìàãàäëàë
á¿õèé îðîí çàéã äàéðóóëàí òàòàõàä ¿¿ñýõ ãàäàðãóóã îðáèòàëü ãýíý.

21. Øðåäèíãåðèéí òýãøèòãýëèéã áîäîõîä 1 îëîí òîîíû õàðèó ãàðäàã. Ò¿¿íèé øèéä
àòîìä îðøèõ ýëåêòðîíû ìàãàäëàë, ò¿¿íèé òºðõèéã èëýðõèéëæ áàéõ ¿¿äíýýñ
õýä õýäýí áîëçëûã òîãòîîæ ºãñºí áàéäàã /Áîðûí ïîñòóëàòûí àäèë/
-ôóíêö òàñðàëòã¿é ,òºãñãºëºã áàéõ ¸ñòîé. Õýðýâ æèæèã õýñýã (e-) ¿ë
òîäîðõîéëîãäîõ íºõöºëä áàéõ ¸ñòîé.
Y -ôóíêö íü íýã óòãàòàé áàéõ ¸ñòîé, ººðººð õýëáýë 1 öýãò íýã ë óòãà àâàõ ¸ñòîé.
Èíãýñýíýýð ýëåêòðîíû òóõàéí öýã äýõ ìàãàäëàëûã òîäîðõîéëíî.
Y
Y = 0
Y ôóíêö íîðì÷ëîãäñîí áàéõ ¸ñòîé. ¯¿íèéã ìàòåìàòèêò äàðààõ áàéäëààð èëýðõèéëíý.
+¥
òY2 = 1
-¥
dV
º/õ îðîí çàéí àëü íýã öýãò èëðýõ ýëåêòðîíû ìàãàäëàë íýã ë áàéíà.
rçàé
ìàãäëàë

22. Õýðýâ ýëåêòðîíû ìàãàäëàëûã 3 õýìæýýñò áºìáºðöºã ãàäàðãóóä òîäîðõîéëæ áàéâàë,
Y = Y(r,q ,j ) j,q, r
áóþó ãýñýí 3 êîîðäèíàòûí ôóíêö áàéäëààð áè÷íý.
j (r,q ,j ) ôóíêö õÿçãààðã¿é îëîí óòãà àâàõ 3 ôóíêöèéí
¿ðæâýð áàéäëààð áè÷èãäýíý.
j(r,q ,j) = R(r)q (q )Y(j)
R(r) ôóíêö íü ýëåêòðîíû öºìººñ àëñëàãäàõ çàéãààñ õàìààðàõ áà
äîëãèîíû ôóíêöèéí ðàäèàëü õýñýã ãýíý
q (q ),y (j ) ôóíêö¿¿äèéã q ,j ºíöã¿¿äýýñ õàìààðàõ äîëãèîíû
ôóíêöèéí ºíöãºí õýñýã ãýíý.
õºäºëæ áóé ýëåêòðîíû r, q ,j êîîðäèíàòààð òîäîðõîéëîãäîõ ìàãàäëàë
Y2 =R2q2Y2
[R(r)]2 - èéã öºìººñ r çàéä àëñëàãäàõ ýëåêòðîíû ìàãàäëàë ãýíý.
[q (q ) ×y (j )]2 -èéã r –ðàäèóñòàé ãàäàðãóó äýýðõ ýëåêòðîíû
ìàãàäëàë ãýíý.

23. Ðàäèàë áîëîí ºíöãºí ôóíêö¿¿äèéí äèôôåðåíöèàë òýãøèòãýëèéã áîäîõîä òîäîðõîé
á¿õýë òîîí óòãóóäààð èëýðõèéëýãäýõ øèéäèéí õàðèó ãàðíà.
q j
sin cos
q j
sin sin
q
cos
x =
r
y =
r
z =
r
( ) ( )
( ) ( )
( ) ( ) e
R r f n l
1
,
f l m
e
2
f m
3
,
=
=
yj
=
qq
äîëãèîíû
òýãøèòãýëèéí
á¿òýí øèéä.
( )
( )
y(j)
R r n = 1, 2, 3, 4 ….
qq
l = 0, 1, 2, 3 ….n-1
ml = -l, -l+1 ….+l
Ìàíäàë êîîðäèíàòàäáîäñîí
äîëãèîíû ôóíêöèéí
õóâèéí øèéä.

24. Äîëãèîíû ôóíêöèéí øèéäèéí õàðèó ml – êâàíòûí òîîã ñîðîíçîí êâàíòûí òîî ãýíý.
Äîëãèîíû ôóíêöèéí ðàäèàëü õýñãýýð òîäîðõîéëîãäîõ êâàíòûí òîî
n áà l –íü öºìººñ ýëåêòðîíû àëñëàãäàõ õýìæýýã òîäîðõîéëîãäîõ òóë ýëåêòðîíû
ýíåðãèéí óòãûã çààäàã. Èéìä ýëåêòðîíû á¿ðýí ýíåðãè n+l -ãýñýí íèéëáýðýýð
òîäîðõîéëîãäîíî.
Äîëãèîíû ôóíêöèéí ºíöãºí õýñãýýð òîäîðõîéëîãäîõ (l, áà me) êâàíòûí òîî íü
ýëåêòðîíû ìàãàäëàë áóþó îðáèòàëèéí õýëáýð ä¿ðñ, îðîí çàéí ÷èãèéã
(l- õýëáýðèéã, me- - ÷èãëýëò ÷àíàðûã) òîäîðõîéëíî
Ìàíäàë êîîðäèíàòàä áîäñîí äîëãèîíû ôóíêöèéí òîäîðõîé íýã õóâèéí øèéä áóþó
êâàíòûí 3 òîîíû íýã áàãöààð òîäîðõîéëîãäîæ áóé ýëåêòðîíû òºëºâ áàéäëûã îðáèòàëü
òºëºâ áóþó îðáèòàëü ãýíý.

25. ÀÒÎÌÛÍ ÎÐÁÈÒÀË ÒªËªÂ ÁÀÉÄÀË
Ýíåðãèéí ò¿âøèí K L M
¯íäñýí ò¿âøèí,
ãîë êâ. òîî
n 1 2 3
Äýä ò¿âøèí,
îðáèòàë êâ. òîî
l 0 0 1 0 1 2
Ñîðîíçîí êâàíòûí
òîî
ml 0 0 -1 0 1 0 -1 0 1 -2 -1 0 1 2
Îðáèòàë òºëºâ 1s 2s 2px 2py 2pz 3s 3px 3py 3pz 3dz
2 3dxy 3dxz 3dyz 3dx
2
y
2
s s p s p d
Îðáèòàëûí òîî 1 4 9
N
4
0 1 2 3
0 -1 0 1 -2 -1 0 1 2 -3 -2 -1 0 1 2 3
4s 4p4p4p4d2 4d4d4d4dx y z z
xy xz yz x
2 4f1 4f2 4f3 4f4 4f5 4f6 4f7
2
y
s p d f
16

26. Àòîìûí îðáèòàëûí ýíåðãèò òºëºâ áºéäàë

27. ÀÒÎÌÛÍ ÎÐÁÈÒÀËÛÍ ÕÝËÝЯ¯Ä , ÎÐÁÈÒÀËÛà ÎÐÎÍ ÇÀÉÍ ÁÀÉÐËÀË
s - îðáèòàë
p - îðáèòàë
d - îðáèòàë

28. ÀÒÎÌÛÍ ÎÐÁÈÒÀËÛÍ ÕÝËÝЯ¯Ä , ÎÐÁÈÒÀËÛà ÎÐÎÍ ÇÀÉÍ ÁÀÉÐËÀË
3 3 2
5
f
3 3 2 -
5
- 3 3 2
x xr
f
y yr
5
z zr
f
-
x ( y2 z2 ) f - z ( y2 x2 ) f y ( x2 z2 ) - f x y z - f

29. 1925 îíä ýðäýìòýí Óéëåíáåê, Ãàóäñìèäò íàð ø¿ëòèéí ìåòàëëûí àòîìûí
ñïåêòðèéí øóãàìûí ìàø íàðèéí ñàëààëàõ ¿çýãäëèã ñóäëàí ýíý íü ýëåêòðîíû
õóâèéí òýíõëýãèéí ýðãýëòòýé õîëáîîòîé ãýæ ¿çñýí.
Õóâèéí òýíõëýãèéí ýðãýëòýýñ ¿¿ñýõ õóâèí ñîðîíçîí ìîìåíòèéã ñïèí ãýæ íýðëýñýí.
Ñïèí êâàíòûí òîî
s s = h ×m
2p
*
Ñïèí êâàíòûí òîî
ms- ýëåêòðîíû áîëîìæèò
õî¸ð óòãûí àëü íýãýíä îðøèæ
áóéã èëýðõèéëíý

30. Îëîí ýëåêòðîíò àòîìûí äîëãèîíû òýãøèòãýë,
ýíåðãèéí ò¿âøèí.
 Øð¸äèíãåðèéí òýãøèòãýëèéí øèéäèéí õàðèó áîëñîí êâàíòûí ãóðâàí òîîíû áàãöààð
òîäîðõîéëîãäîõ ýëåêòðîíû îðøèõ ìàãàäëàë áóþó îðáèòàë òºëºâ áàéäëóóä íü íýã
ýëåêòðîíîîñ òîãòñîí H –èéí àòîìûí òîãòîëöîîíä õèéãäñýí áîëîâ÷ òýäãýýð ýëåêòðîíû
îðøèõ ìàãàäëóóä á¿õ àòîìä àäèë õàäãàëàãäàíà ãýæ ¿çäýã.
 Íýãýýñ äýýø ýëåêòðîíòîé àòîìûã îëîí ýëåêòðîíò àòîì ãýäýã áºãººä òýäãýýð
ýëåêòðîíóóä ýëåêòðîí îðøèõ ìàãàäëàë (îðáèòàë) -ä òîäîðõîé ç¿é òîãòëîîð áàéðëàäàã.
 Îëîí ýëåêòðîíò àòîì äàõü ýëåêòðîí íü öºìòýé õàðèëöàí ¿éë÷ëýõèéí çýðýãöýý Êóëîíû
ò¿ëõýëöýë õ¿÷ýýð áèå áèåòýéãýý õàðèëöàí ¿éë÷ëýõ òóë òýäãýýðèéí äîëãèîíû
ôóíêö¿¿ä ìºí áèå áèåäýý íºëººëíº.
 Ãýâ÷ ýíý õàðèëöàí ¿éë÷ëýëèã òîîöñîí Øð¸äèíãåðèéí òýãøèòãýëèéí áîäîëò õàðààõàí
õèéãäýýã¿é áàéíà. Èéìä îëîí àòîì äàõü ýëåêòðîíû òºëºâ áàéäëûã îéðîëöîîëîõ àðãààð
øèéäíý.

31. Îéðîëöîî òîîöîëîõ àðãûã Òîìàñà, Ôåðìè íàð õýðýãëýí ¿åëýõ ñèñòåìèéí
èõýíõ ýëåìåíòèéí ñòàòèê çàãâàð ãàðàí ýëåêòðîí ¿¿ëíèé ºíöãºí òàðõàëòûã
îéðîëöîîãîîð òîäîðõîéëñîí.
Îéðîëöîî òîîöîîëîõ àðãûã õýðýãëýñýíýýð äàðààõ ä¿ãíýëòýä õ¿ðñýí:
 Îëîí ýëåêòðîíò àòîìûí ýëåêòðîíû õàðèëöàí ¿éë÷ëýë äîëãèîíû ôóíêöèéí çºâõºí
ðàäèóñûí õýñýãò íºëººëíº ªíöãºí õýñýãò áóþó îðáèòàëèéí õýëáýðò íºëººëºõã¿é
 Ýëåêòðîíû ýíåðãè ãîë êâàíòûí òîî áà îðáèò êâàíò òîîíû ýíåðãèéí íèéëáýð (n+l)
-ýýð òîäîðõîéëîãäîíî.
 Îëîí ýëåêòðîíò àòîì äàõü ýëåêòðîíû òºëºâ áàéäàë H-èéí ýëåêòðîíû àäèë
êâàíòûí 4 òîîíû óòãààð èëýðõèéëýãäýíý (n, l, ml, ms ).
 Îðáèòàëèééí ýíåðãè íýã àòîìààñ íºãººä øèëæèõýä ýëåìåíòèéí äýñ äóãààðààñ
õàìààðàí ººð÷ëºãäºíº.

32. ÀÒÎÌÛÍ ÎÐÁÈÒÀË ÝËÅÊÒÐÎÍÎÎÐ ÁªÃ˪ÃÄªÕ Ç¯É ÒÎÃÒÎË
Àòîìûí îðáèòàëûí ýíåðãèéí äàðààëàë
Ýíåðãèéí ºñºõ äàðààëàë Ïàóëûí õîðèãèéí çàð÷èì Õóíäûí ä¿ðýì
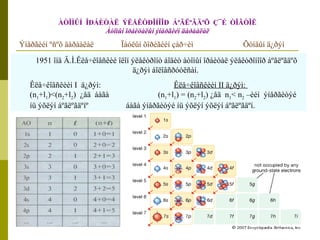
1951 îíä Â.Ì.Êëå÷êîâñêèé îëîí ýëåêòðîíò áîäèò àòîìûí îðáèòàë ýëåêòðîíîîð áºãëºãäºõ
ä¿ðýì áîëîâñðóóëñàí.
Êëå÷êîâñêèéí I ä¿ðýì: Êëå÷êîâñêèéí II ä¿ðýì:
(n1+l1)<(n2+l2) ¿åä áàãà (n1+l1) = (n2+l2) ¿åä n1< n2 –èéí ýíåðãèòýé
íü ýõëýí áºãëºãäºíº áàãà ýíåðãèòýé íü ýõëýí ýõëýí áºãëºãäºí.

33. Ïàóëèéí õîðèãèéí çàð÷èì:
Àòîì õè÷íýýí ýëåêòðîíòîé áàéñàí êâàíòûí
äºðâºí òîî äºðâ¿¿ëýý èæèë õî¸ð ýëåêòðîí
áàéäàãã¿é.
̺ðäëºãºº: Íýã îðáèòàëä ýñðýã ñïèíòýé
õî¸ðîî èë¿¿ ýëåêòðîí áºãëºãäºõã¿é
Àòîìûí ýëåêòðîíò á¿òýö
Õóíäûí ä¿ðýì:
̺õººãäñºí áóþó èæèë ýíåðãèòýé
ðáèòàëüä ýëåêòðîí áºãëºãäºõ人 ñïèí
êâàíòûí òîîíû íèéëáýð àëü èõ áàéõààð
áºãëºãäºíº.
̺ðäëºãºº: Èæèë ýíåðãèòýé îðáèòàëüä
ýëåêòðîíóóä ãàíö, ãàíöààð, ñïèíû
÷èãëýë èæèë áàéõààð áºãëºãäºíº.

34. Àòîìûí îðáèòàë ýëåêòðîíîîð áºãëºãäºõ ä¿ðýì çºð÷èãäºõ îíöãîé
òîõèîëäîë:
Æèøýý íü : Cr, Cu
2 2 6 2 6 4 2 5 1
Cr s s p s p d s Þ
d s
1 2 2 3 3 3 4 3 4
Cu s s p s p d s d s
2 2 6 2 6 9 2 10 1
24
29
Þ
1 2 2 3 3 3 4 3 4
d - îðáèòàëèéí õóâüä ýëåêòðîí íü èæèë ñïèíòýé äàí ýëåêòðîí áîëîí
ñºðºã ñïèíòýé õîñ ýëåêòðîíîîð á¿ðýí ä¿¿ðãýãäñýí òîõèîëäîëä
îðáèòàëü ýíåðãèéí õàìãèéí òîãòâîðòîé òºëºâä îðøèíî.