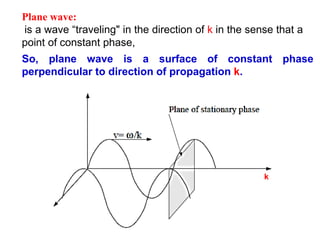
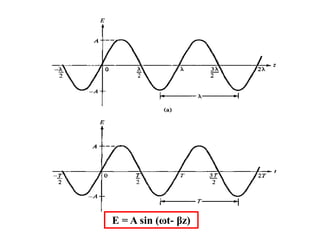
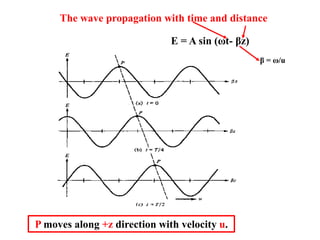
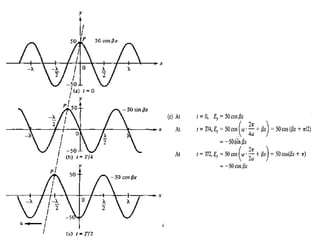
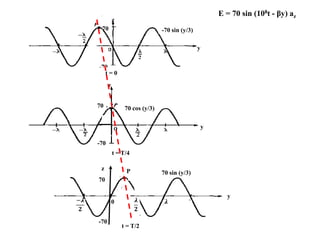
The lecture by Dr. Ahmed Abouelmagd focuses on electromagnetic wave propagation and how to derive electromagnetic wave motion in various media using Maxwell's equations. It discusses plane waves, their characteristics, and provides examples of wave equations in one-dimensional space. The document also includes calculations related to wave propagation, direction, and sketching the wave at different time intervals.

1. Lecture – 3
Dr. Ahmed Abouelmagd
Electromagnetic Fields
COMM 320
ELECTROMAGNETIC WAVE PROPAGATION
Plane Waves
Elgazeera High Institute for
Engineering and Technology

2. Waves are means of transporting energy or information
A wave is a function of both space and time.
Our goal is to solve Maxwell's equations and derive EM
wave motion in the following media:
ɛ ….. Permittivity
μ ….. Permeability
σ ….. Conductivity

3. So, plane wave is a surface of constant phase
perpendicular to direction of propagation k.
Plane wave:
is a wave “traveling" in the direction of k in the sense that a
point of constant phase,
k

4. Plane Waves
in Uniform Linear Isotropic Nonconducting Medium
Therefore: the Maxwell’s equations become:
For the above medium:

5. The Wave Equation:
Take the curl of Faraday's law curl equation:
As ( . E = 0 ), this equation may be written as:

6. Take the curl of Ampere's law curl equation, and follow the same
previous steps:
Thus any Cartesian component of E or B obeys a classical
wave equation of the form
where v = c/ 𝜇𝜀.
Complex traveling wave solution to this equation:

7. Wave moves along k direction with a speed v which is w/k.
This solution is a wave “traveling" in the direction of k in the
sense that a point of constant phase, meaning: k.x - wt = constant,
𝝏𝒖𝒌
𝝏𝒙

8. V …. Electric scalar potential
A…. magnetic vector potential
Wave equation:
In one dimension, a scalar wave equation takes the form of:
E = A sin (ωt- βz)
The solution of this equation:
u is the wave speed , ω is the angular frequency (in
radians/second); β is the phase constant or wave number,
β = ω/u = 2π/λ (in radians/meter).
Wave equation in one dimension

9. E = A sin (ωt- βz)

10. P moves along +z direction with velocity u.
β = ω/u
E = A sin (ωt- βz)
The wave propagation with time and distance

11. Solution 1
Example 1
The electric field in free space is given by:
E = 50 cos (108t + βx) ay V/m
(a) Find the direction of wave propagation.
(b) Calculate β and the time it takes to travel a distance of λ/2.
(c) Sketch the wave at t=0, T/4, and T/2)
(a) Compare E = 50 cos (108t + βx) ay with wave equation
solution : E = A sin (ωt- βz)
The direction of wave propagation is x
(b) In free space, u = c.
β = w/u= w/c = 108 / 3 (108) = 1/3

12. Time t1 wave takes to travel a distance of λ/2:
β = 2π/λ
1/3 = 2π/λ
λ = 2π/(1/3) = 6π
λ/2 = 3π
As the wave travels in free space, the wave velocity = light
velocity c, therefore:
t1 = (λ/2 )/c = 3π/3(10)8 = 31.42 ns
E = 50 cos (108t + βx) ay V/m

14. z
y
-70 sin (y/3)
70
-70
t = 0
t = T/4
70 cos (y/3)
-70
z
y
70
0 𝝀
𝟐
−𝝀
𝟐
𝝀
y
z P
70
-70
70 sin (y/3)
t = T/2
E = 70 sin (108t - βy) az