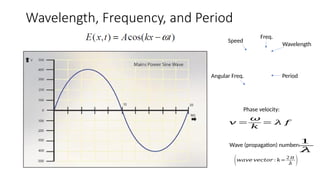
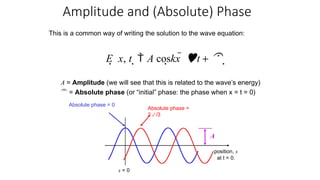
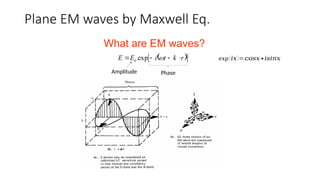
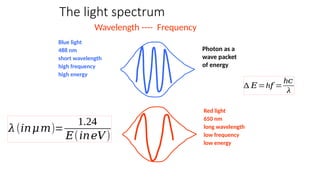
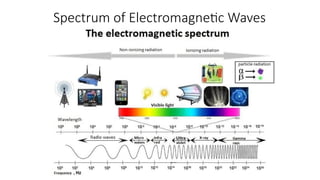
The document covers the basics of wave theory, focusing on the electromagnetic spectrum and the propagation of light as a wave. It explains the wave equation, the relationship between wavelength, frequency, and period, and distinguishes between longitudinal and transverse waves. Additionally, it highlights the characteristics of electromagnetic waves including amplitude, phase, and photon emission during electronic transitions.


![Solution of Wave Equation
0
v2
2
E
1 2
E
x2
t
2
In 1-D
The wave equation has the simple solution:
E x, t E x
vt
where E(t) [an f (u)] can be any twice-differentiable function.
(1)](https://image.slidesharecdn.com/lecture1introductiontowavesbasicconcepts-241203195402-cc5d89ad/85/Introduction-to-waves-basic-concepts-pptx-4-320.jpg)