Recommended
PPTX
PPTX
PPTX
PPTX
vFabric for i ISVs and MSPs
PPTX
Workab Presentation Day 4
PDF
PDF
PDF
CV Sarah Stefanini - Español
PDF
Certificado de Referencia Estadual
DOC
PPTX
PDF
PPTX
PPTX
PDF
PDF
Zimbra COMO DEBEMOS UTILIZARLO
PDF
PPTX
PPS
PDF
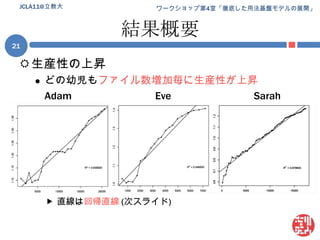
DOC
Secretarias municipais as (1)
DOCX
TXT
PDF
Fórum dos Leitores - O Estado de S. Paulo
PPTX
PPTX
Funcionamiento de un pila2
PDF
Informe Económico Mensual
PPT
Diálogos Capitais - Imazon
PDF
PDF
パターン・ランゲージ3.0研究会(2nd Season)第2回
More Related Content
PPTX
PPTX
PPTX
PPTX
vFabric for i ISVs and MSPs
PPTX
Workab Presentation Day 4
PDF
PDF
PDF
CV Sarah Stefanini - Español
Viewers also liked
PDF
Certificado de Referencia Estadual
DOC
PPTX
PDF
PPTX
PPTX
PDF
PDF
Zimbra COMO DEBEMOS UTILIZARLO
PDF
PPTX
PPS
PDF
DOC
Secretarias municipais as (1)
DOCX
TXT
PDF
Fórum dos Leitores - O Estado de S. Paulo
PPTX
PPTX
Funcionamiento de un pila2
PDF
Informe Económico Mensual
PPT
Diálogos Capitais - Imazon
Similar to Jcla11 ws research
PDF
PDF
パターン・ランゲージ3.0研究会(2nd Season)第2回
PPTX
PPTX
2014 NECTJ JHL Annual Conference Language Curriculum and Classroom
PDF
PDF
第8回山口県英語教育フォーラム(亘理スライド公開版)
PDF
企業向け「パターン・ランゲージ3.0研究会」第3回スライド
PPTX
PDF
PPT
Generalization of the Concept of Pattern Language
PDF
20111207 勉強会のパターンを書いてみるワークショップ
PPTX
PDF
PDF
知識構成型ジグソー法を用いた協調学習 ― 21世紀に向けた学習スタイル ― (2015)
PDF
PDF
PPT
Pattern mining-scrum gatheringtokyo20130115
PPTX
PDF
Ppp8 20151220watari公開版key
PDF
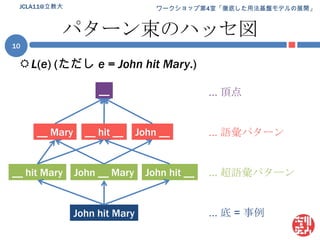
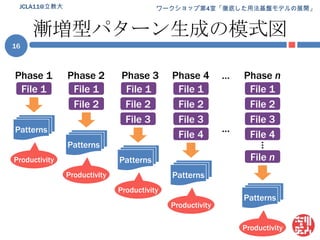
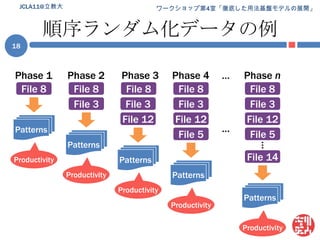
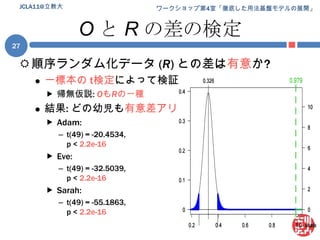
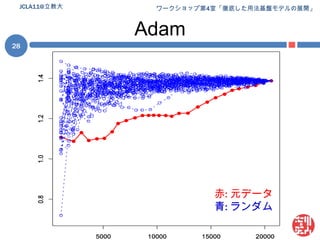
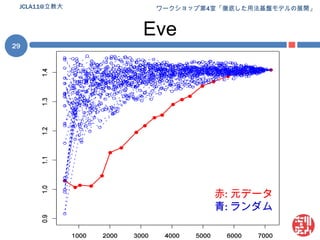
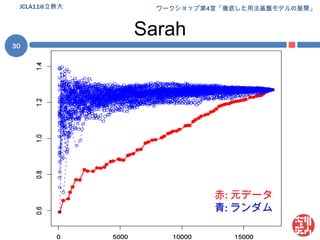
Jcla11 ws research 1. 2. 3. 4. 5. 6. 7. 8. 9. パターン束 (パターンラティス)パターン集合 P(e) の性質pi, pj∈P(e) に部分一致に基づく継承関係を規定可能= 継承関係 (is-a) を「順序」とする半順序集合継承関係を含むパターン集合P(e) = パターン束 L(e)継承関係の図示 (次スライド)e = John hit Maryの場合のL(e)をハッセ図により図示継承関係は推移律を満たすので冗長な関係は除いてある簡略化のため連続する変項は単一化してあるE.g., [John, __, __ ] [John, __ ]JCLA11@立教大9 10. 11. パターンの発達としての統語発達パターン = 統語知識の実体なら統語発達 = パターンの発達パターンの発達:a. 利用可能なパターンの総数の増加b. 個々のパターンの性質(e.g., 生産性, 複雑性) の成長注意幼児の統語知識が「XXX構文」となっている保証無し一語文 ~ 語彙依存構文は具体的な語が指定済み以上からパターン =構文の「候補」として網羅的に調査具体的には上記 b について調査 (評価対象は「生産性」)JCLA11@立教大11 12. 13. 14. 方法 [1](前処理)上記データから (前処理)幼児 = {Adam, Eve, Sarah} の発話のみを抜き出し言いさし・重複, ポーズの含まれる発話を除外前処理後のデータの詳細 (Eve) は予稿集 (p. xxx) 参照JCLA11@立教大14*CHI: Shadow .*CHI: read Shadow # Mommy .*CHI: read Shadow .*CHI: Shadow .*CHI: who (th)at ?*MOT: what is that ?*CHI: lollipop .*MOT: +" he sticks to me like +...*CHI: +, glue .*MOT: +" and scares away +...*CHI: piggie squeak .*CHI: wee wee way home .ポーズ母親の発話重複 15. 16. 漸増型パターン生成の模式図JCLA11@立教大16Phase 1Phase 2Phase 3Phase 4…Phase nFile 1File 1File 1File 1File 1File 2File 2File 2File 2File 3File 3File 3Patterns…File 4File 4Patterns…PatternsFile nProductivityPatternsProductivityProductivityPatternsProductivityProductivity 17. 18. 順序ランダム化データの例JCLA11@立教大18Phase 1Phase 2Phase 3Phase 4…Phase nFile 8File 8File 8File 8File 8File 3File 3File 3File 3File 12File 12File 12Patterns…File 5File 5Patterns…PatternsFile 14ProductivityPatternsProductivityProductivityPatternsProductivityProductivity 19. 生産性の算定生産性尺度 = シャノンのエントロピー(H)以降単に「エントロピー」or H各変項 (v) に対して計算変項 vのエントロピー (H(v)) :(ただし: p(wi) = i番目の実現値の生起確率)変項が複数ある場合 (e.g., Put __ in __):それぞれの変項に対してエントロピーを計算し各値を合計変項間「共変動率」を見積もり合計値を補正補正の詳細は吉川 (2010) 参照JCLA11@立教大19 20. 21. 22. 23. 24. 25. 26. 線形回帰増加の傾向は?線形回帰 (linear regression) によって確認目的変数: エントロピーの平均値説明変数: データ量(発話数)決定係数(R2) = 回帰の当てはまり度合い ≤ 1Adam: 0.96; Eve: 0.95; Sarah: 0.98軒並み高水準順序ランダム化データ(R)との比較Rにもそれぞれ線形回帰を実施“R2 ≥ 0.5”のデータに対し元データ(O)と傾きを比較線形の傾向と言えそうなものを選抜結果 Oと R諸データ間で傾きの違いは顕著JCLA11@立教大26 27. Oと Rの差の検定順序ランダム化データ (R) との差は有意か?一標本の t検定によって検証帰無仮説:OもRの一種結果: どの幼児も有意差アリAdam:t(49) = -20.4534,p < 2.2e-16Eve:t(49) = -32.5039,p < 2.2e-16Sarah:t(49) = -55.1863,p < 2.2e-16JCLA11@立教大27 28. 29. 30. 31. 32. 33. 34. 35. 課題 + 宣伝(統計的) 評価方法の不在線形回帰による比較は試験的なもの本当にうまく結果が評価できているか?この点に関しては日本認知科学会 第27回大会 (JCSS 2010)における発表「パターンの生産性に見る統語発達」by 吉川本発表とある意味相補的な内容JCSS 2010 @ 神戸大学鶴甲第1キャンパス (2010/9/17 ~ 19)吉川の発表は初日(9/17)論文は以下からダウンロード可能http://www.jcss.gr.jp/meetings/JCSS2010/proceedings.html35JCLA11@立教大 36. 37. 38. 追加の参考文献Borensztajn, G., Zuidema,W., & Bod, R. 2009. Children's grammars grow more abstract with age: Evidence from an automatic procedure for identifying the productive units of language. Topics in Cognitive Science, 1 (1), 175–188.JCLA11@立教大38 39.






![パターンの定義 [1]パターン束理論 (PLT)によるパターンの定義任意の事例 eを分節モデルTで分節化 分節列T(e)を得るeの例: John hit Mary.Tの例: 単語分節T(e)の例: [John, hit, Mary]7JCLA11@立教大John hahitMary= eJohn分節化= T(e)hitMaryJohn](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-7-320.jpg)
![パターンの定義 [2]パターンの定義の続きT(e) の分節を一つずつ変項 Xによって置換この産物をパターンと定義この工程を全分節が変項化されるまで再帰的に適用得られた産物 = eのパターン集合 P(e)JCLA11@立教大8hitMaryJohnパターンhitMary____MaryJohnhit__John](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-8-320.jpg)
![パターン束 (パターンラティス)パターン集合 P(e) の性質pi, pj∈P(e) に部分一致に基づく継承関係を規定可能= 継承関係 (is-a) を「順序」とする半順序集合継承関係を含むパターン集合P(e) = パターン束 L(e)継承関係の図示 (次スライド)e = John hit Maryの場合のL(e)をハッセ図により図示継承関係は推移律を満たすので冗長な関係は除いてある簡略化のため連続する変項は単一化してあるE.g., [John, __, __ ] [John, __ ]JCLA11@立教大9](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-9-320.jpg)


![データデータにはCHILDES内のBrownコーパスを使用JCLA11@立教大13CHILDESEnglish(USA)Japanese…BrownMacWhinney…AdamEveSarah…2;3–3;4 [4;10]28/55 files1;6–2;320 files2;3–3;8[5;1]71/139 files](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-13-320.jpg)
上記データから (前処理)幼児 = {Adam, Eve, Sarah} の発話のみを抜き出し言いさし・重複, ポーズの含まれる発話を除外前処理後のデータの詳細 (Eve) は予稿集 (p. xxx) 参照JCLA11@立教大14*CHI: Shadow .*CHI: read Shadow # Mommy .*CHI: read Shadow .*CHI: Shadow .*CHI: who (th)at ?*MOT: what is that ?*CHI: lollipop .*MOT: +" he sticks to me like +...*CHI: +, glue .*MOT: +" and scares away +...*CHI: piggie squeak .*CHI: wee wee way home .ポーズ母親の発話重複](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-14-320.jpg)
![方法[2] (漸増型パターン生成)生産性の算定 (漸増型パターン生成)各幼児1ファイル目のデータからパターンを生成ファイルは時系列に沿って番号(id)付けされている“頻度 ≥ 2” かつ “バリエーション ≥ 2” のものを選抜選抜パターンに対し生産性を算定・平均を算出以降nファイルある内の i = 2 ~ nまで1 ~ iファイル目のデータから上記のプロセスを繰り返すJCLA11@立教大15](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-15-320.jpg)
![方法 [3] (順序ランダム化)ただし漸増型パターン生成で生産性平均の上昇が示される それは単にデータの量が増えたからでは??幼児の知識の質的変化ではなく知識量の変化の現れ??「段階的習得プロセス」「統語発達」は示せないそこで順序ランダム化データを複数 (50パターン) 用意これを R= {r1, r2, r3, … r50} とするそれぞれに対し漸増型パターン生成を実施結果をオリジナルデータと比較JCLA11@立教大17](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-17-320.jpg)


![得られたパターンの例 [~10]JCLA11@立教大22](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-22-320.jpg)
![得られたパターンの例 [11~20]JCLA11@立教大23](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-23-320.jpg)
![得られたパターンの例 [21~28]JCLA11@立教大24](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-24-320.jpg)








![謝辞本ワークショップ参加メンバー黒田 航氏(情報通信研究機構)長谷部 陽一郎氏 (同志社大学)淺尾 仁彦氏 (ニューヨーク州立大学バッファロー校[院])慶應義塾大学大学院 井上逸兵研究会メンバー井上 逸兵教授(慶應義塾大学)中村 文紀氏 (慶應義塾大学[院])統計検定の補助久保田 ひろい氏 (千葉大学[院])JCLA11@立教大37](https://image.slidesharecdn.com/jcla11wsresearch-110112110753-phpapp01/85/Jcla11-ws-research-37-320.jpg)

