Downloaded 13 times
Uploaded byVon Ryan Sugatan
Introduction to Computer Lesson 5.0
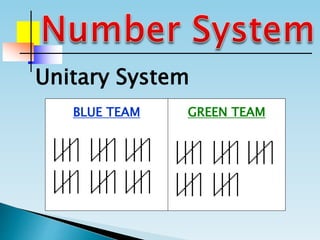
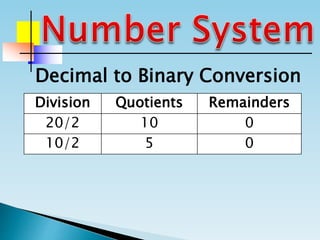
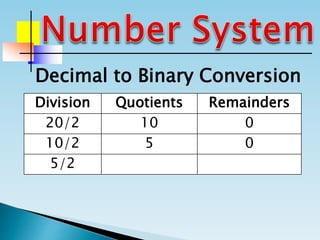
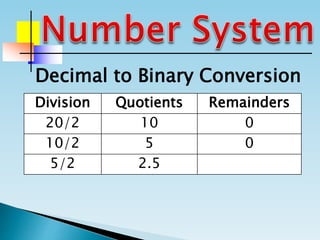
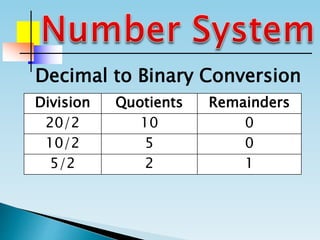
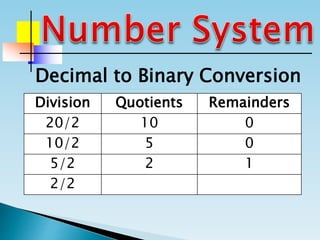
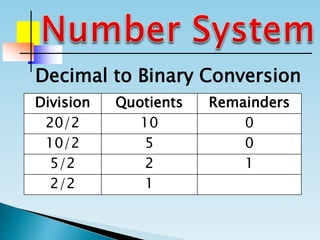
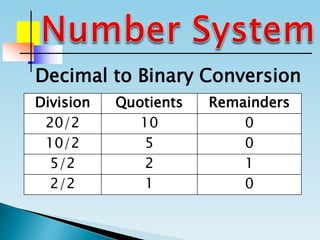
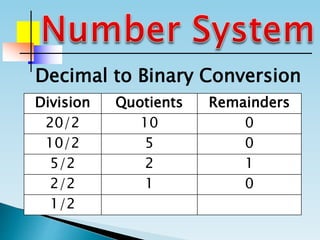
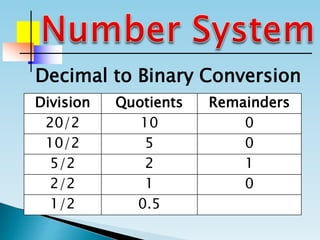
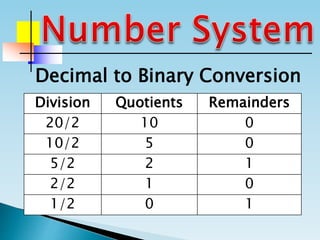
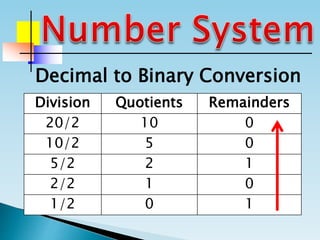
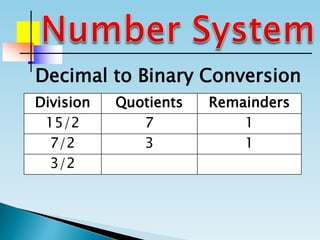
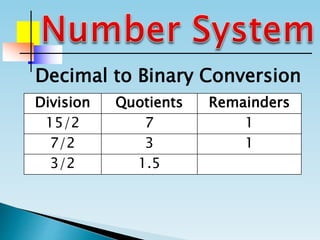
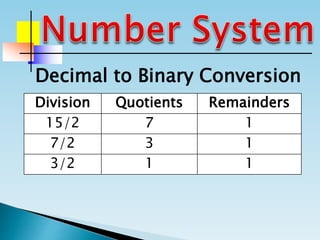
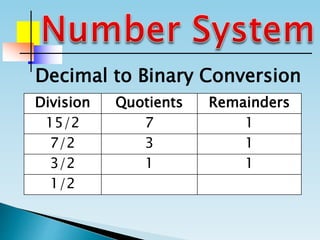
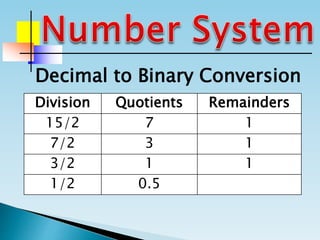
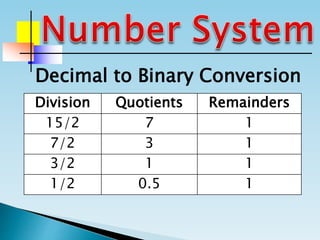
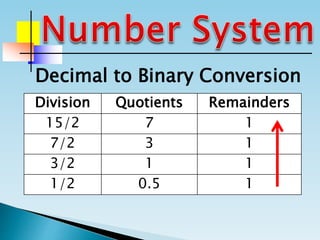
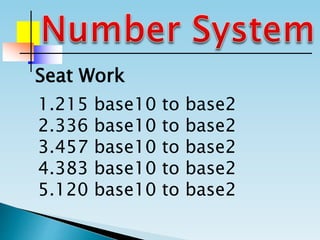
The document discusses the binary number system and how to convert between decimal and binary numbers. It explains that binary uses only the digits 0 and 1 and that each digit has a place value determined by its position. To convert a decimal number to binary, you repeatedly divide the number by 2 and write down the remainders with the rightmost remainder first. Similarly, to convert a binary number to decimal, you multiply each digit by its place value and add the results. Several examples are provided to demonstrate converting specific numbers between decimal and binary representations.
Introduction to Computer Lesson 5.0
- 1. By: Vhonz Sugatan POWERSchool
- 3.
- 4. Unitary System BLUE TEAMGREEN TEAM
- 5.
- 6. Decimal System 0, 1,2, 3, 4, 5, 6, 7, 8, 9
- 7.
- 8.
- 9.
- 10.
- 11.
- 12.
- 13.
- 14.
- 15.
- 16.
- 17. Decimal to BinaryConversion
- 18. Step 1 Decimal toBinary Conversion
- 19. Divide the decimalnumber by 2 and record the remainder. Step 1 Decimal to Binary Conversion
- 20. Step 2 Decimal toBinary Conversion
- 21. Continue to divideby 2 as long as the resulting quotient is not equal to zero. Step 2 Decimal to Binary Conversion
- 22. Step 3 Decimal toBinary Conversion
- 23. The binary equivalentof the number consists of the remainders listed from right to left. Step 3 Decimal to Binary Conversion
- 24. Example: Convert 20 (base10) to its binary equivalent. Decimal to Binary Conversion
- 25. Division Quotients Remainders 20/2 Decimalto Binary Conversion
- 26. Division Quotients Remainders 20/210 Decimal to Binary Conversion
- 27. Division Quotients Remainders 20/210 0 Decimal to Binary Conversion
- 28. Division Quotients Remainders 20/210 0 10/2 Decimal to Binary Conversion
- 29. Division Quotients Remainders 20/210 0 10/2 5 Decimal to Binary Conversion
- 30. Division Quotients Remainders 20/210 0 10/2 5 0 Decimal to Binary Conversion
- 31. Division Quotients Remainders 20/210 0 10/2 5 0 5/2 Decimal to Binary Conversion
- 32. Division Quotients Remainders 20/210 0 10/2 5 0 5/2 2.5 Decimal to Binary Conversion
- 33. Division Quotients Remainders 20/210 0 10/2 5 0 5/2 2 1 Decimal to Binary Conversion
- 34. Division Quotients Remainders 20/210 0 10/2 5 0 5/2 2 1 2/2 Decimal to Binary Conversion
- 35. Division Quotients Remainders 20/210 0 10/2 5 0 5/2 2 1 2/2 1 Decimal to Binary Conversion
- 36. Division Quotients Remainders 20/210 0 10/2 5 0 5/2 2 1 2/2 1 0 Decimal to Binary Conversion
- 37. Division Quotients Remainders 20/210 0 10/2 5 0 5/2 2 1 2/2 1 0 1/2 Decimal to Binary Conversion
- 38. Division Quotients Remainders 20/210 0 10/2 5 0 5/2 2 1 2/2 1 0 1/2 0.5 Decimal to Binary Conversion
- 39. Division Quotients Remainders 20/210 0 10/2 5 0 5/2 2 1 2/2 1 0 1/2 0 1 Decimal to Binary Conversion
- 40. Division Quotients Remainders 20/210 0 10/2 5 0 5/2 2 1 2/2 1 0 1/2 0 1 Decimal to Binary Conversion
- 41. Example: 20 (base 10)to its binary equivalent is 10100 (base 2) Decimal to Binary Conversion
- 42. Example: Convert 15 (base10) to its binary equivalent. Decimal to Binary Conversion
- 43. Division Quotients Remainders 15/2 Decimalto Binary Conversion
- 44. Division Quotients Remainders 15/27.5 Decimal to Binary Conversion
- 45. Division Quotients Remainders 15/27 1 Decimal to Binary Conversion
- 46. Division Quotients Remainders 15/27 1 7/2 Decimal to Binary Conversion
- 47. Division Quotients Remainders 15/27 1 7/2 3.5 Decimal to Binary Conversion
- 48. Division Quotients Remainders 15/27 1 7/2 3 1 Decimal to Binary Conversion
- 49. Division Quotients Remainders 15/27 1 7/2 3 1 3/2 Decimal to Binary Conversion
- 50. Division Quotients Remainders 15/27 1 7/2 3 1 3/2 1.5 Decimal to Binary Conversion
- 51. Division Quotients Remainders 15/27 1 7/2 3 1 3/2 1 1 Decimal to Binary Conversion
- 52. Division Quotients Remainders 15/27 1 7/2 3 1 3/2 1 1 1/2 Decimal to Binary Conversion
- 53. Division Quotients Remainders 15/27 1 7/2 3 1 3/2 1 1 1/2 0.5 Decimal to Binary Conversion
- 54. Division Quotients Remainders 15/27 1 7/2 3 1 3/2 1 1 1/2 0.5 1 Decimal to Binary Conversion
- 55. Division Quotients Remainders 15/27 1 7/2 3 1 3/2 1 1 1/2 0.5 1 Decimal to Binary Conversion
- 56. Example: 15 (base 10)to its binary equivalent is 1111 (base 2) Decimal to Binary Conversion
- 57. Binary to DecimalConversion
- 58. Binary to DecimalConversion Example: Convert 10100 (base 2) to its decimal equivalent.
- 59. Binary to DecimalConversion Example: 10100 (base 2)
- 60. Binary to DecimalConversion Example: 10100 (base 2) 1 0 1 0 0
- 61. Binary to DecimalConversion Example: 10100 (base 2) 1 0 1 0 0X2+ X2+ X2+ X2+ X2
- 62. Binary to DecimalConversion Example: 10100 (base 2) 1 0 1 0 0X2+ X2+ X2+ X2+ X2 01234
- 63. Binary to DecimalConversion Example: 10100 (base 2) 1 0 1 0 0X2+ X2+ X2+ X2+ X2 01234 0
- 64. Binary to DecimalConversion Example: 10100 (base 2) 1 0 1 0 0X2+ X2+ X2+ X2+ X2 01234 00
- 65. Binary to DecimalConversion Example: 10100 (base 2) 1 0 1 0 0X2+ X2+ X2+ X2+ X2 01234 004
- 66. Binary to DecimalConversion Example: 10100 (base 2) 1 0 1 0 0X2+ X2+ X2+ X2+ X2 01234 0040
- 67. Binary to DecimalConversion Example: 10100 (base 2) 1 0 1 0 0X2+ X2+ X2+ X2+ X2 01234 004016
- 68. Binary to DecimalConversion Example: 10100 (base 2) 1 0 1 0 0X2+ X2+ X2+ X2+ X2 01234 ++++ 004016
- 69. Binary to DecimalConversion Example: 10100 (base 2) 1 0 1 0 0X2+ X2+ X2+ X2+ X2 01234 ++++ 004016 20
- 70. 10100 (base 2)to its decimal equivalent is 20 (base 10) Binary to Decimal Conversion
- 71. Binary to DecimalConversion Example: Convert 1111 (base 2) to its decimal equivalent.
- 72. Binary to DecimalConversion Example: 1111 (base 2)
- 73. Binary to DecimalConversion Example: 1111 (base 2) 1 1 1 1
- 74. Binary to DecimalConversion Example: 1111 (base 2) 1 1 1 1X2+ X2+ X2+ X2
- 75. Binary to DecimalConversion Example: 1111 (base 2) 1 1 1 1X2+ X2+ X2+ X2 0123
- 76. Binary to DecimalConversion Example: 1111 (base 2) 1 1 1 1X2+ X2+ X2+ X2 0123 1
- 77. Binary to DecimalConversion Example: 1111 (base 2) 1 1 1 1X2+ X2+ X2+ X2 0123 12
- 78. Binary to DecimalConversion Example: 1111 (base 2) 1 1 1 1X2+ X2+ X2+ X2 0123 124
- 79. Binary to DecimalConversion Example: 1111 (base 2) 1 1 1 1X2+ X2+ X2+ X2 0123 1248
- 80. Binary to DecimalConversion Example: 1111 (base 2) 1 1 1 1X2+ X2+ X2+ X2 0123 1248 +++
- 81. Binary to DecimalConversion Example: 1111 (base 2) 1 1 1 1X2+ X2+ X2+ X2 0123 1248 +++ 15
- 82.
- 83. Seat Work 1.215 base10to base2 2.336 base10 to base2 3.457 base10 to base2 4.383 base10 to base2 5.120 base10 to base2
Editor's Notes
- #3 It is a fact that we use numbers for counting – that is to express quantities. From simple to complex expressions, we use numbers every day. At a very young age, we were taught (aside from the abcs) how to count 1 to 100. The reason for this is that ability to count is one essential skill that we need in life. In counting, the simplest is the. (CLICK NEXT TO CONTINUE)
- #4 Is a one-to-one comparison between the objects to be counted and the count or tally. We commonly use this in keeping track of scores in a basketball game or volleyball game. (CLICK NEXT TO CONTINUE)
- #5 This system is composed of vertical and horizontal marks which are divided into groups of five. The unitary system is simple and straightforward, but the way it is represent is a waste of writing time and space. It is also not ideal to be used in complicated calculations. We used the.. (CLICK NEXT TO CONTINUE)
- #6 The ingenious method of expressing all numbers by means of ten symbols originated from India. It is widely used and is based the ten fingers of human being The decimal number system is the system you and I use everyday. It makes use of ten numeric symbols (CLICK NEXT TO CONTINUE)
- #7 The decimal number system is called base 10 system. This is because the base of any number system is equal to the number of basic symbol used in that system. Since there are 10 basic number symbols in the decimal number system (numbers 0 – 9), it has a base of 10. We normally identify each basic numeric symbol by one of the following values. What are those values (CLICK NEXT TO CONTINUE)
- #8 The Inherent Value of a numeric symbol is the value of that symbol standing alone. Any number is still related somehow to its basic value regardless of how it appears in number system. For example what number is this. (CLICK NEXT TO CONTINUE)
- #9 (CLICK NEXT TO CONTINUE)
- #10 6 is related to the quantity six, even if it is used in different number positions, like 216, 161, or 617. Yet, in each of these examples, the symbol 6 does not really equal to the inherent value of the quantity six. This is because of. (CLICK NEXT TO CONTINUE)
- #11 The Positional Value of a numeric symbol is directly related to the base of a number system. In the decimal system, each position has a value 10 times greater than the position to its right. For example the number (CLICK NEXT TO CONTINUE)
- #12 (CLICK NEXT TO CONTINUE)
- #13 the symbol 3 represents the ones (or units) position. (CLICK NEXT TO CONTINUE)
- #14 the symbol 2 represents the tens position (10 x 1), (CLICK NEXT TO CONTINUE)
- #15 and the symbol 4 represents the hundreds position (10 x 10). In other words, each move to the left represents an increase in the value of the position by factor of ten. This is because the base of the decimal number system is ten. (CLICK NEXT TO CONTINUE)
- #16 The binary number system is a base 2 system. In other words, there are only to numeric symbols used in the binary system. Kaya hindi mahirap mag bilang. ( ,”) (CLICK NEXT TO CONTINUE)
- #17 this does not mean, however, that the binary system can only represent the value of zero (0), one (1), ten (10), eleven (11), and so on. In fact, any value represented in decimal can be represented in binary and vise-versa. This is made possible by the concepts of inherent and positional value. The binary to decimal representation is called (CLICK NEXT TO CONTINUE)
- #18 In binary- to decimal conversion, The division – multiplication method is one approach used in converting a decimal number to its binary equivalent. These are the steps to be followed in decimal to binary conversion. (CLICK NEXT TO CONTINUE)
- #19 (CLICK NEXT TO CONTINUE)
- #20 (CLICK NEXT TO CONTINUE)
- #21 (CLICK NEXT TO CONTINUE)
- #22 (CLICK NEXT TO CONTINUE)
- #23 (CLICK NEXT TO CONTINUE)
- #24 When the obtained quotient is equal to zero, The binary equivalent of the number consists of the remainders listed from right to left. (bottom to top) in the order way they were recorded. Example: (CLICK NEXT TO CONTINUE)
- #25 (CLICK NEXT TO CONTINUE)
- #26 (CLICK NEXT TO CONTINUE)
- #27 (CLICK NEXT TO CONTINUE)
- #28 (CLICK NEXT TO CONTINUE)
- #29 (CLICK NEXT TO CONTINUE)
- #30 (CLICK NEXT TO CONTINUE)
- #31 (CLICK NEXT TO CONTINUE)
- #32 (CLICK NEXT TO CONTINUE)
- #33 (CLICK NEXT TO CONTINUE)
- #34 (CLICK NEXT TO CONTINUE)
- #35 (CLICK NEXT TO CONTINUE)
- #36 (CLICK NEXT TO CONTINUE)
- #37 (CLICK NEXT TO CONTINUE)
- #38 (CLICK NEXT TO CONTINUE)
- #39 (CLICK NEXT TO CONTINUE)
- #40 (CLICK NEXT TO CONTINUE)
- #41 (CLICK NEXT TO CONTINUE)
- #42 Another example? (CLICK NEXT TO CONTINUE)
- #43 (CLICK NEXT TO CONTINUE)
- #44 (CLICK NEXT TO CONTINUE)
- #45 (CLICK NEXT TO CONTINUE)
- #46 (CLICK NEXT TO CONTINUE)
- #47 (CLICK NEXT TO CONTINUE)
- #48 (CLICK NEXT TO CONTINUE)
- #49 (CLICK NEXT TO CONTINUE)
- #50 (CLICK NEXT TO CONTINUE)
- #51 (CLICK NEXT TO CONTINUE)
- #52 (CLICK NEXT TO CONTINUE)
- #53 (CLICK NEXT TO CONTINUE)
- #54 (CLICK NEXT TO CONTINUE)
- #55 (CLICK NEXT TO CONTINUE)
- #56 (CLICK NEXT TO CONTINUE)
- #57 Now if you want to check if your answer is correct you can check it. Using the other way. That is called (CLICK NEXT TO CONTINUE)
- #58 In order to do it the other way around, the expanded notation approach is used. In this approach, the position values of the original numeral are written out. Let us look at some examples. My 1st example in the decimal to binary is 20. (CLICK NEXT TO CONTINUE)
- #59 (CLICK NEXT TO CONTINUE)
- #60 (CLICK NEXT TO CONTINUE)
- #61 (CLICK NEXT TO CONTINUE)
- #62 (CLICK NEXT TO CONTINUE)
- #63 (CLICK NEXT TO CONTINUE)
- #64 (CLICK NEXT TO CONTINUE)
- #65 (CLICK NEXT TO CONTINUE)
- #66 (CLICK NEXT TO CONTINUE)
- #67 (CLICK NEXT TO CONTINUE)
- #68 (CLICK NEXT TO CONTINUE)
- #69 (CLICK NEXT TO CONTINUE)
- #70 (CLICK NEXT TO CONTINUE)
- #71 Gets? Or you want another example? (CLICK NEXT TO CONTINUE)
- #72 (CLICK NEXT TO CONTINUE)
- #73 (CLICK NEXT TO CONTINUE)
- #74 (CLICK NEXT TO CONTINUE)
- #75 (CLICK NEXT TO CONTINUE)
- #76 (CLICK NEXT TO CONTINUE)
- #77 (CLICK NEXT TO CONTINUE)
- #78 (CLICK NEXT TO CONTINUE)
- #79 (CLICK NEXT TO CONTINUE)
- #80 (CLICK NEXT TO CONTINUE)
- #81 (CLICK NEXT TO CONTINUE)
- #82 Question guys?? (CLICK NEXT TO CONTINUE)
- #83 Question guys?? (CLICK NEXT TO CONTINUE)
- #84 Question guys?? 1.) 11010111 2.) 101010000 3.) 111001001 4.) 101111111 5.) 1111000 ` (CLICK NEXT TO CONTINUE)