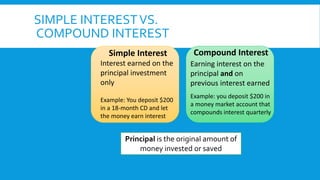
This document discusses the power of compound interest for savings and investments. It explains that compound interest is earned on both the principal amount and accumulated interest over time. This leads to much higher returns compared to simple interest, where interest is only earned on the principal. The document uses online calculators and examples to demonstrate how factors like investment amounts, interest rates, and length of time impact compound growth. It emphasizes that starting investments earlier and allowing interest to compound more frequently can significantly increase the total accumulated value of savings and retirement accounts.

1. SAVING AND
INVESTING
TARGET
EXPLAIN HOW SAVINGS AND
INVESTING CONTRIBUTETO
FINANCIALWELL-BEING,
BUILDING WEALTH, AND HELPING
MEET PERSONAL FINANCIAL
GOALS
USEAN ONLINECOMPOUND INTEREST
CALCULATORTO CALCULATETHETOTAL
AMOUNTAN INDIVIDUALWOULD HAVE IN A
SAVINGSOR RETIREMENT ACCOUNT
IDENTIFYWHAT FACTORS IMPACT
COMPOUNDING AND HOW
EXPLAIN WHY COMPOUNDING CAN BE A
POWERFUL SAVINGAND INVESTING
STRATEGY
Meet short-term
goals
Keep funds secure
while growing
Simple interest
 Plan for long-term goals
like retirement
 More risk for more return
on an investment
 Compound interest-
interest on initial principal
and all accumulated
interest
(I = P [(1 + i)n -1]

2. THETOTAL COST OF BORROWING: LOAN
BASICS
 Principal- the original amount of money
borrowed or that is still owed
 Interest- the price you are paying for
the use of someone else’s money,
typically expressed as a rate (%)
 APR- the interest rate on loans, credit,
etc., that reflects the annual cost of
borrowing money
 Loan term- the length of the loan

3. Simple Interest Compound Interest
SIMPLE INTERESTVS.
COMPOUND INTEREST
Interest earned on the
principal investment
only
Example: You deposit $200
in a 18-month CD and let
the money earn interest
Earning interest on the
principal and on
previous interest earned
Example: you deposit $200 in
a money market account that
compounds interest quarterly
Principal is the original amount of
money invested or saved

4. Simple Interest vs.
Compound Interest
• What is compound interest? How can you
use it to increase your savings?Watch this
video and then answer the following
questions.
• How does the age a person starts saving
at impact the amount they can earn in
compound interest?
• Today’s savings accounts do not offer
interest rates much higher than 1%. How
does this impact the power of
compounding?

5. Principal -How much was borrowed.
Time - How long it was borrowed for.
(in years)
Rate -
(annual % rate)
What interest was charged.
Amount to Payback = Principal + Interest
Interest = Principal  Rate  Time
I P r t
  
TheTotal Cost of Borrowing: Calculating Interest

6. Joe borrows $200 from the bank at 6% simple
interest for 3 years. What interest does he owe,
and what is his total balance (amount to payback)?
Interest Balance
I P r t
  
I  (200)(0.06)(3)
I 36

Interest owed $36

Balance = P + I
Balance = 200 + 36
Balance = 236
Balance = $236
P 200

r 6%
 0.06

t 3


7. Juan invests $5000 in bonds for 6 months at an
annual interest rate of 7%. How much interest
did he earn, and what is the balance in his account?
Interest Balance
I P r t
  
I (5000)(0.07)(0.5)
I 175

Interest owed $175

Balance = P + I
Balance = 5000 + 175
Balance = 5175
Balance = $5175
P 5000

r 7%
 0.07

t 6 months
 0.5 years


8. Compound Interest
for a Single Deposit
Investment = $1,402.55
Simple Interest =
$1,350.00
COMPARING SIMPLEVERSUS
COMPOUND INTEREST
Why are they different?
By reinvesting the interest earned,
the interest payment keeps growing
as interest is compounded on
interest

9. SMART INVESTING
Every variable
in the formula
impacts the
amount of
your return
P = Principal
The larger the principal
investment, the greater your return
R = Interest Rate
The higher the interest rate, the
greater your return
N = # ofTimes Interest is
Compounded perYear
The more often the interest is
compounded, the greater your
return.
T = Number ofYears
The longer you leave your money
in the investment, the greater your
return
Rule of Thumb:
The higher the variable, the
greater your return

10. “Compound interest is the 8th
wonder of the world. He who
understands it earns it. He
who doesn’t pays it.
Compound interest is the
most powerful force in the
universe.”
Albert Einstein

11. “How many millionaires do you know who
have become wealthy by investing in
savings accounts? I rest my case.”
-Robert G. Allen

12.  Starting at age 19, Ben invested $2,000 a
year for 8 years. ($16,000 total)
 Starting at age 27, Arthur invested $2,000
a year for the next 39 years. ($78,000)
THE STORY OF BEN
AND ARTHUR

13. COMPOUND INTEREST
 Number of times interest is compounded has effect on return
 Compounding more frequently equals higher returns
$1,000 invested at 7% for 5 years
Compounding
Method
Compounded
how often?
Amount
Investment is
Worth
Daily 365
Monthly 12
Quarterly 4
Semi-annually 2
Annually 1
$1,419.02
$1,417.63
$1,414.78
$1,410.60
$1,402.55
Click
Here