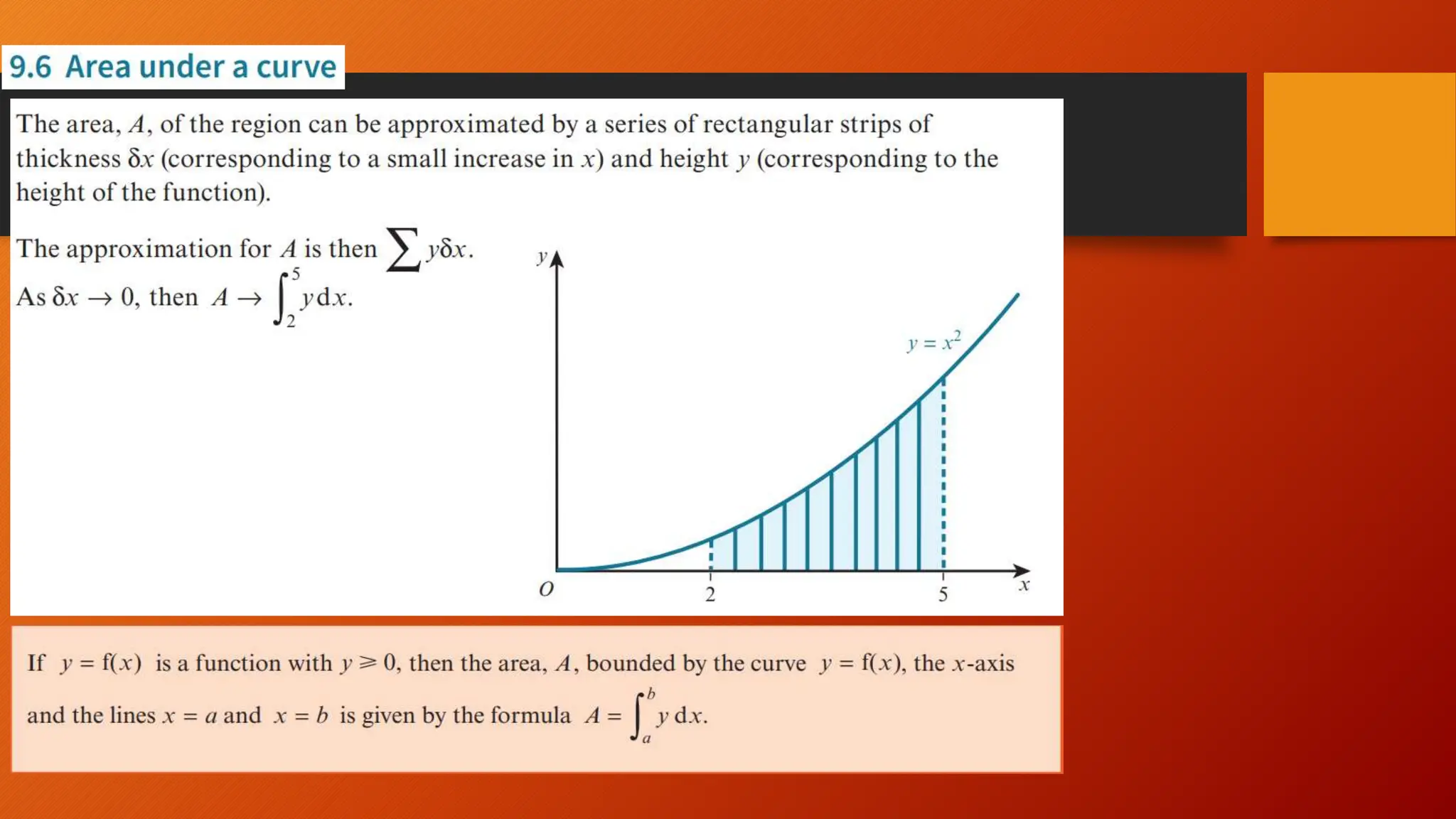
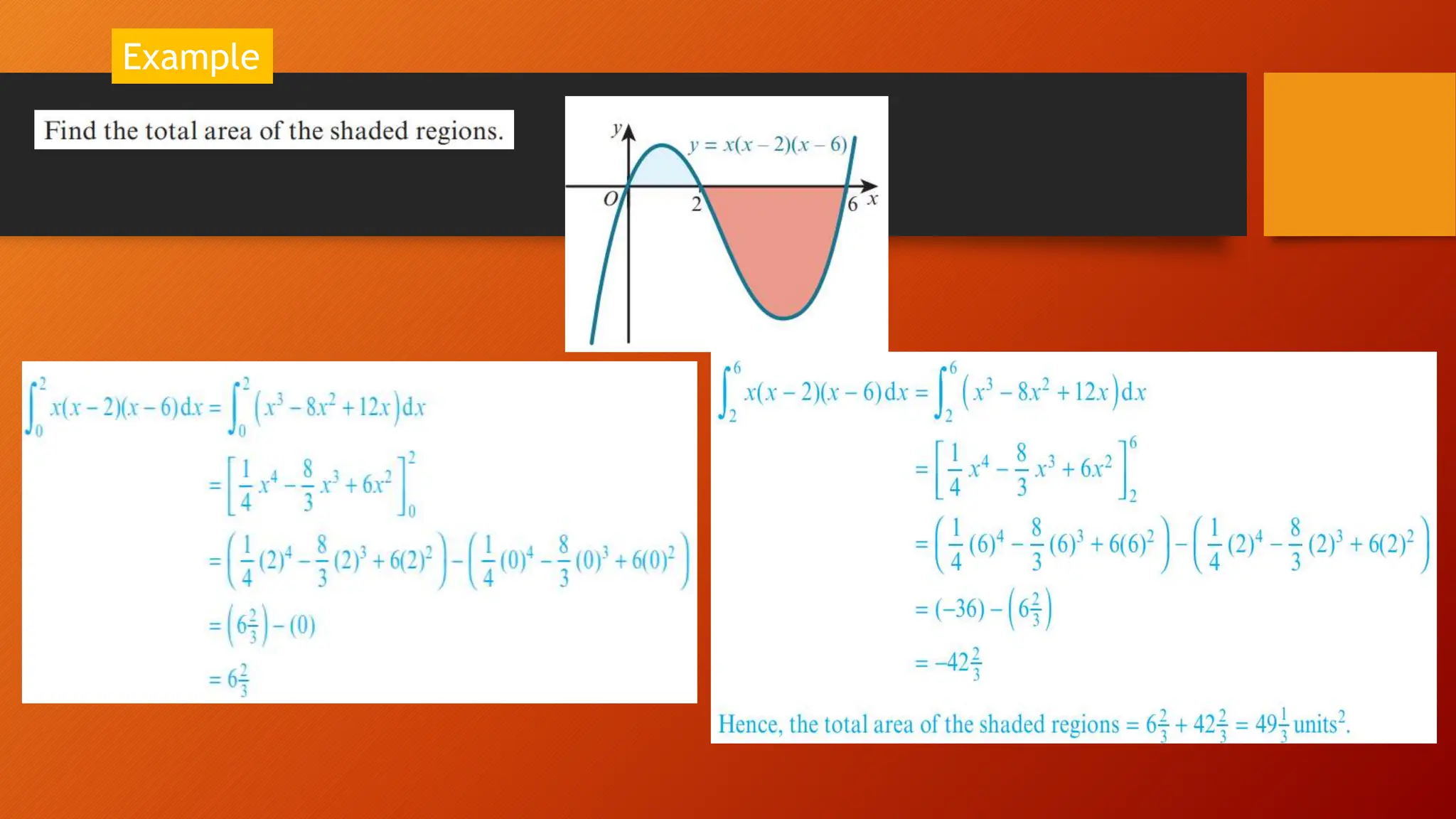
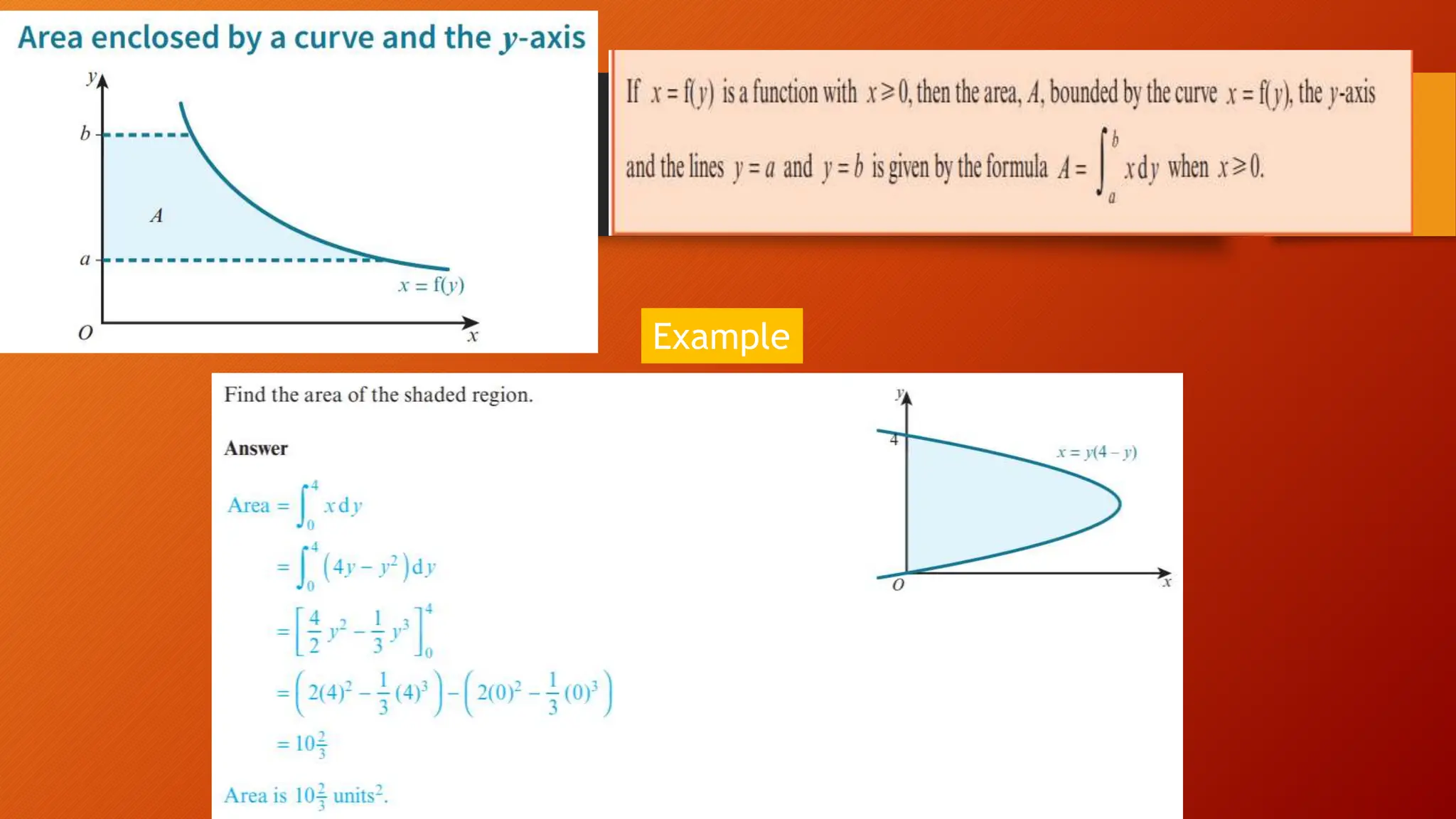
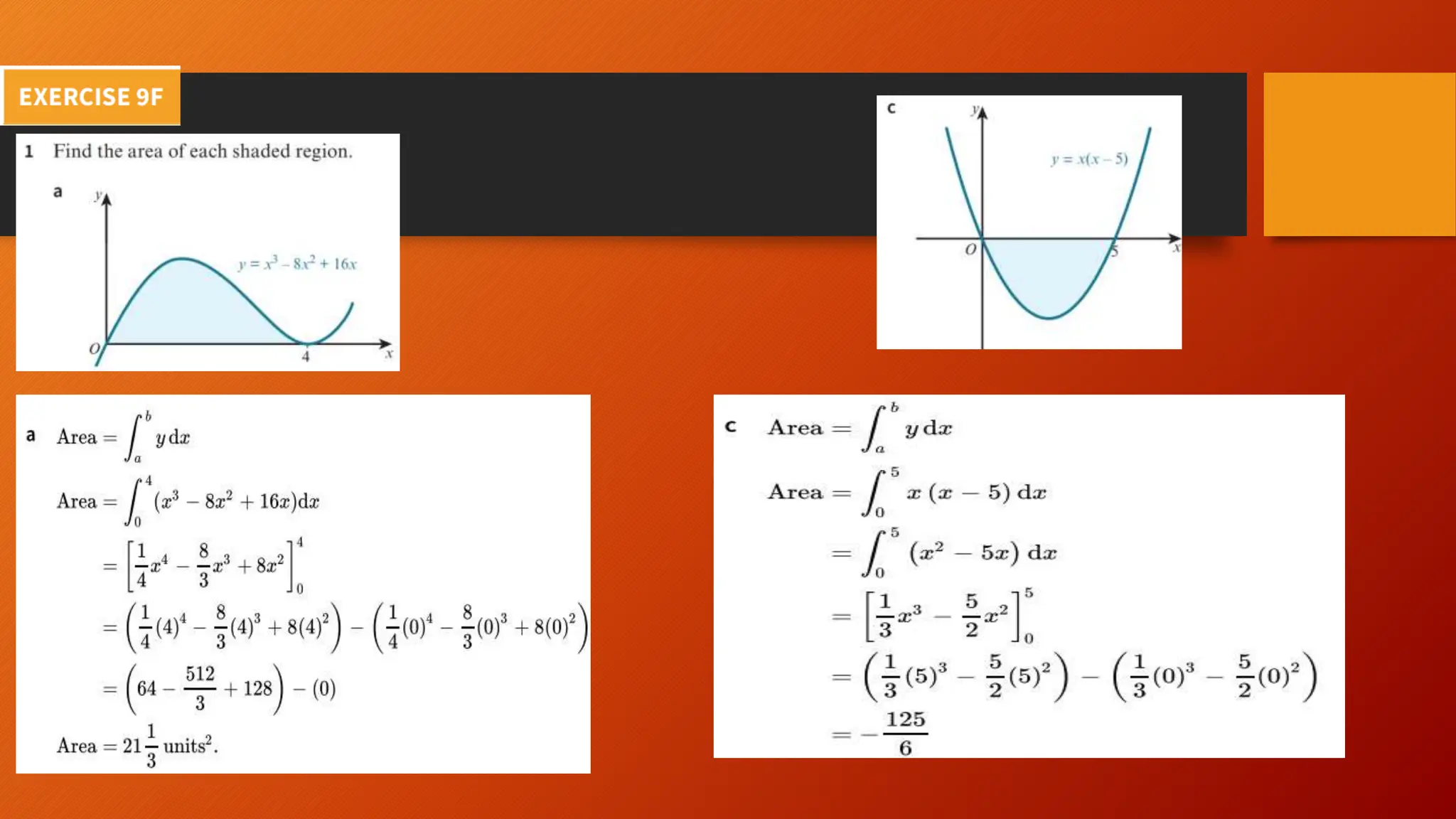
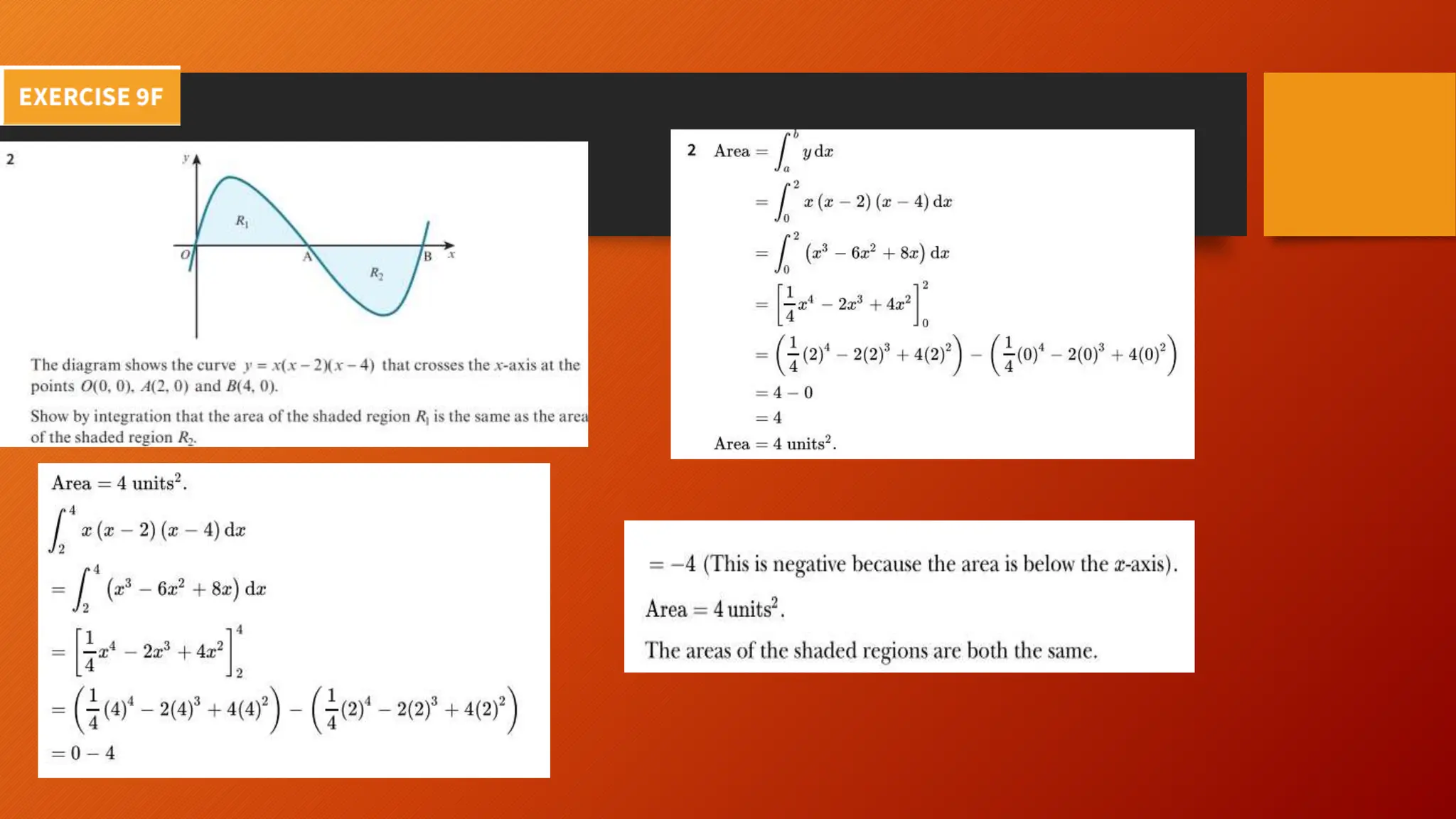
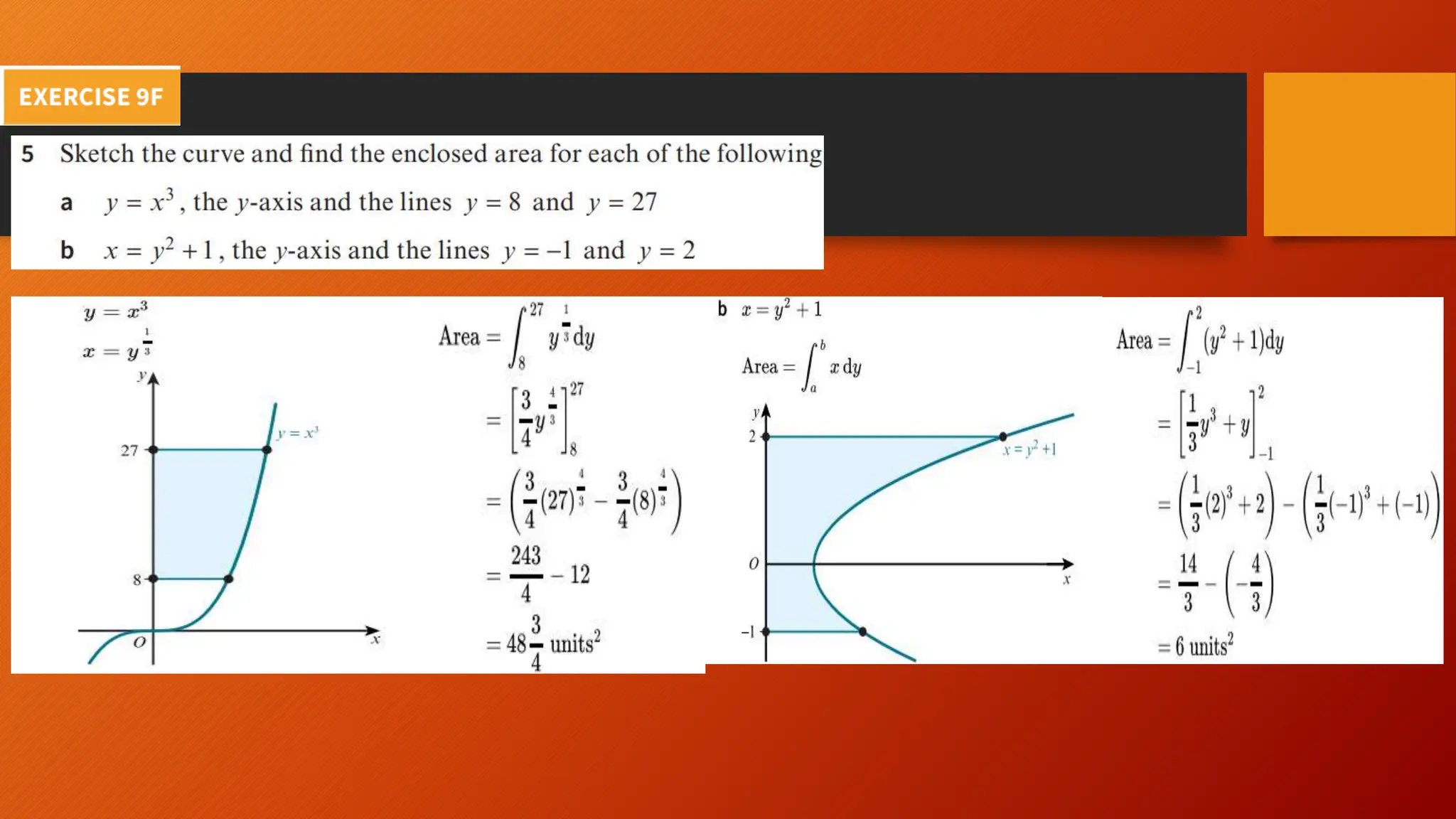
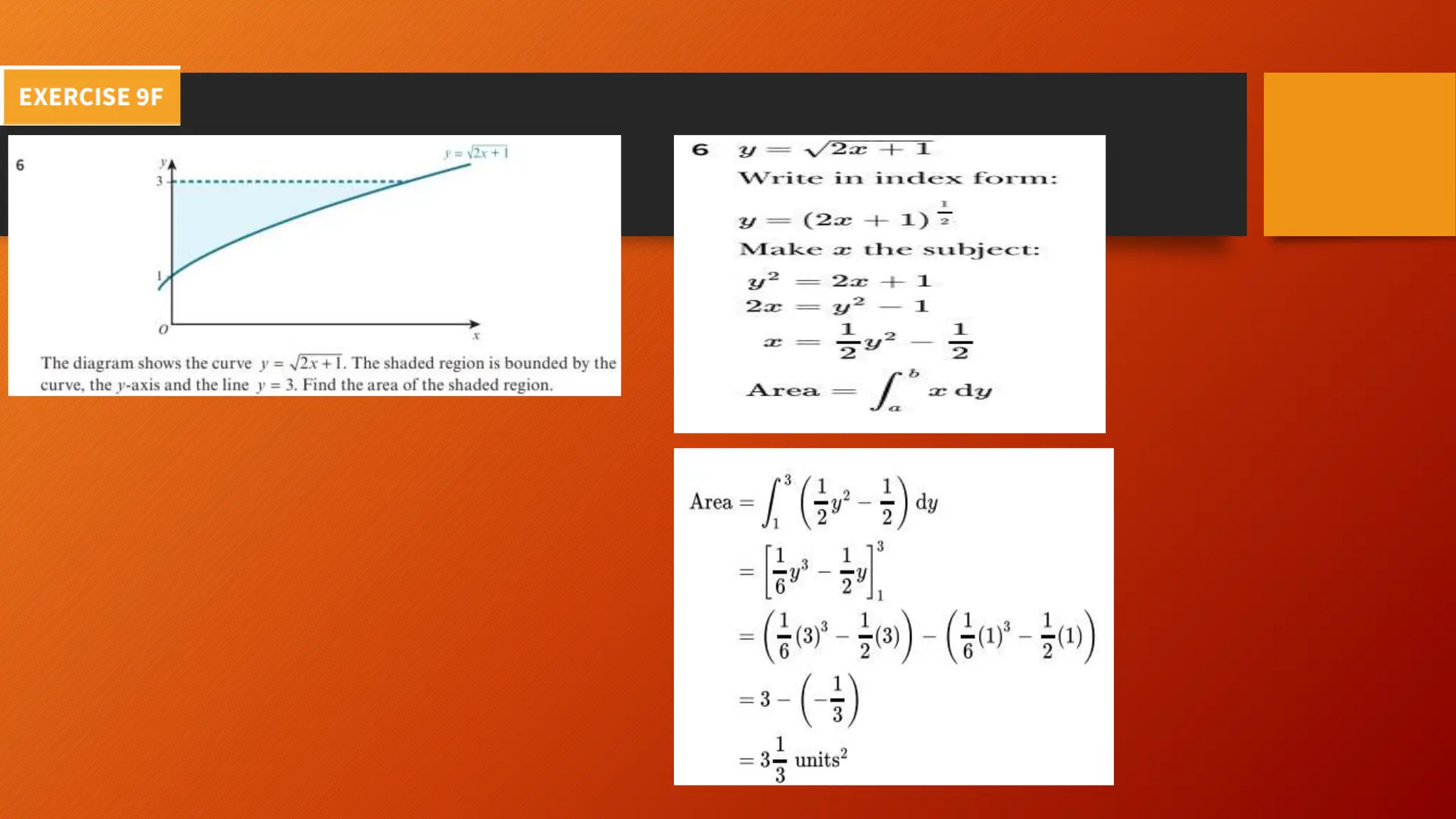
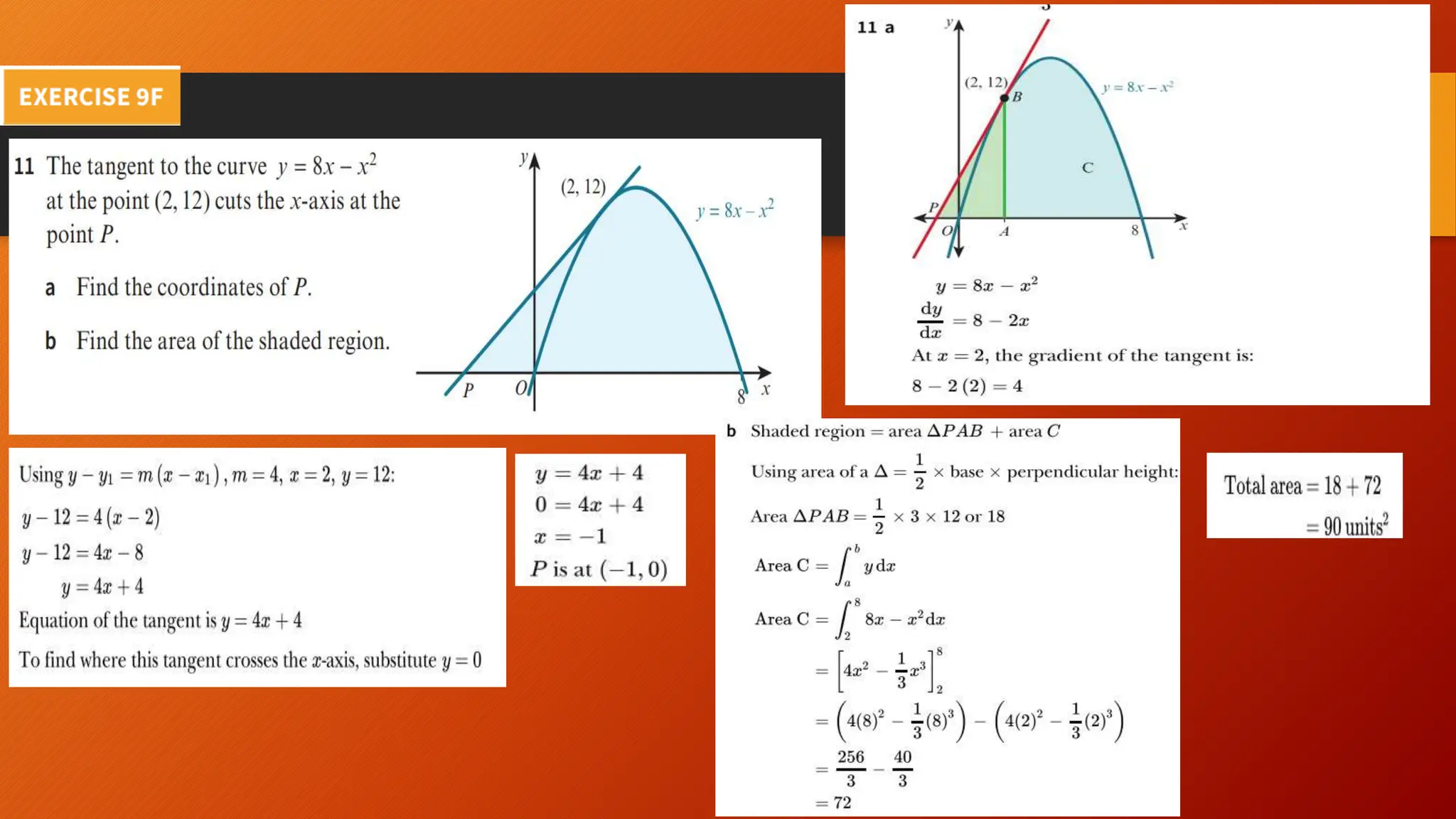
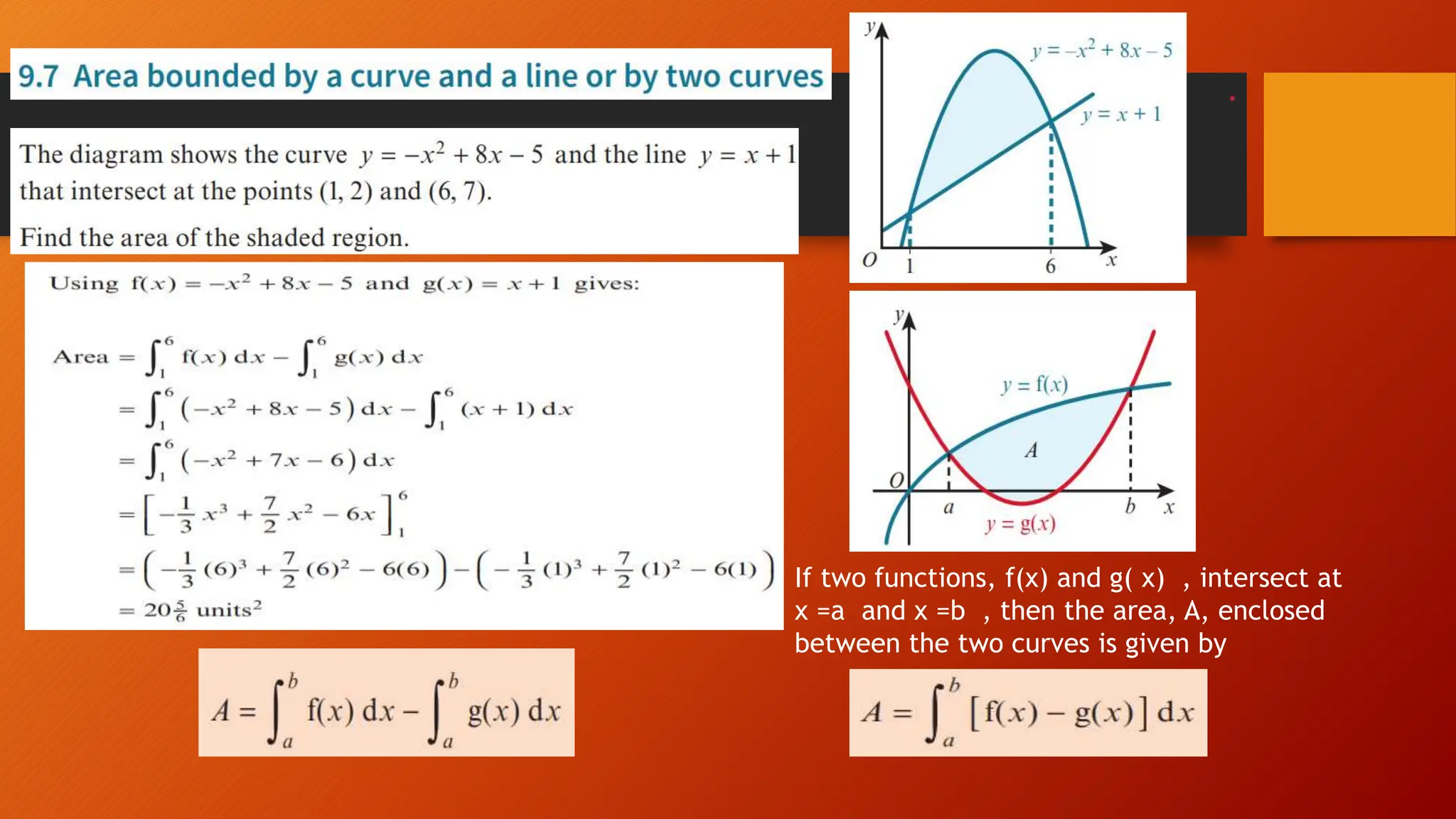
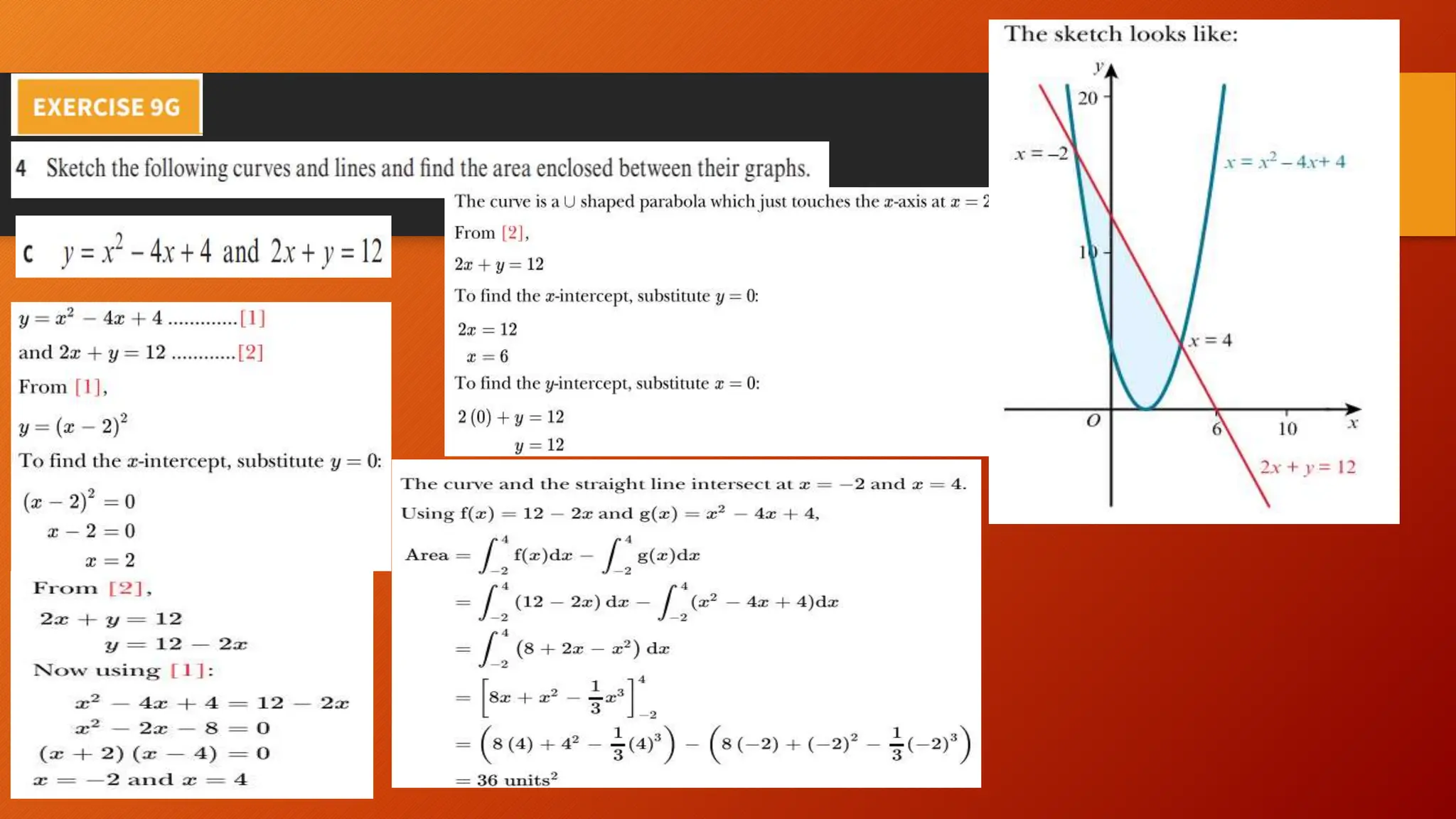
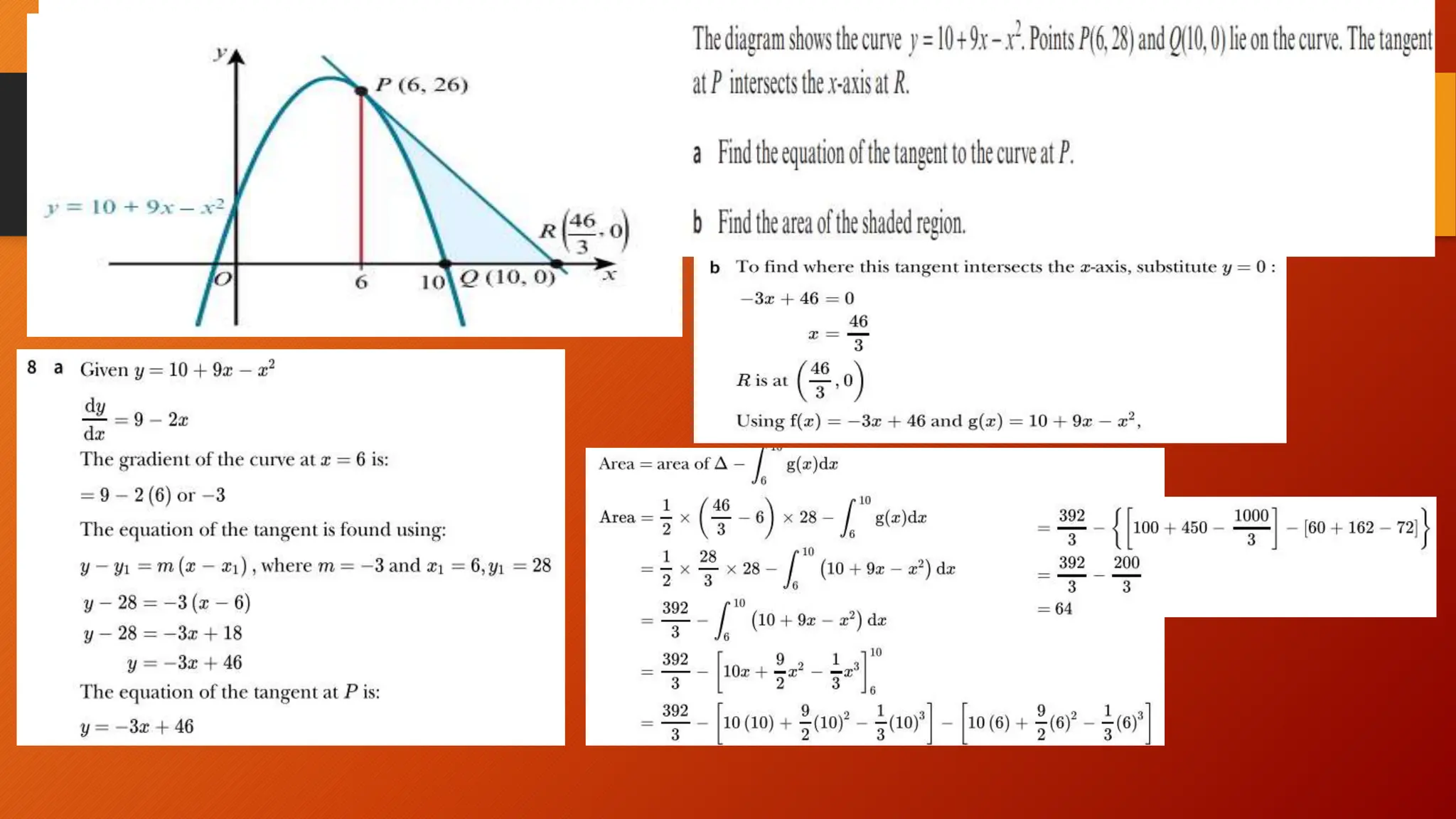
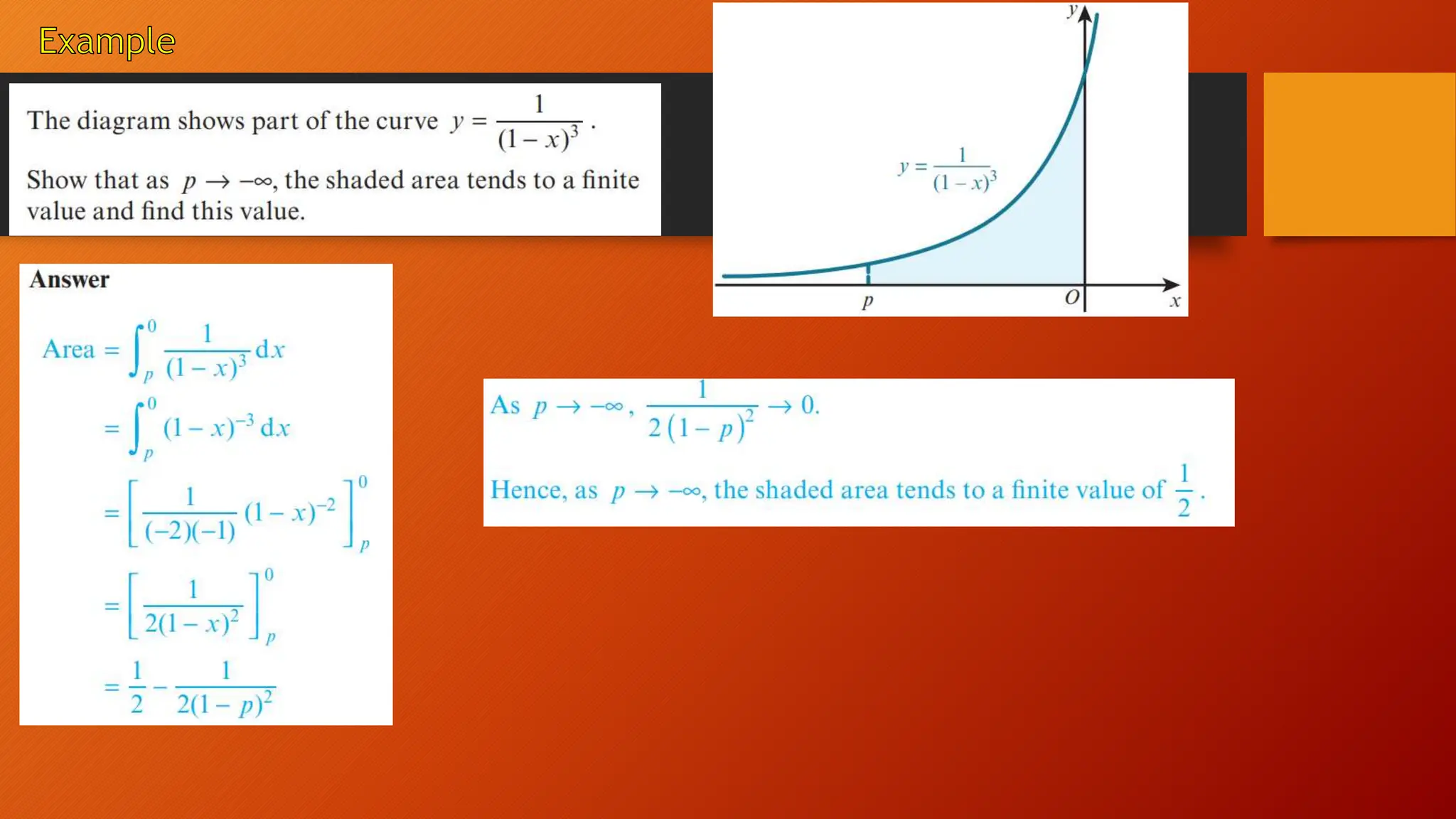
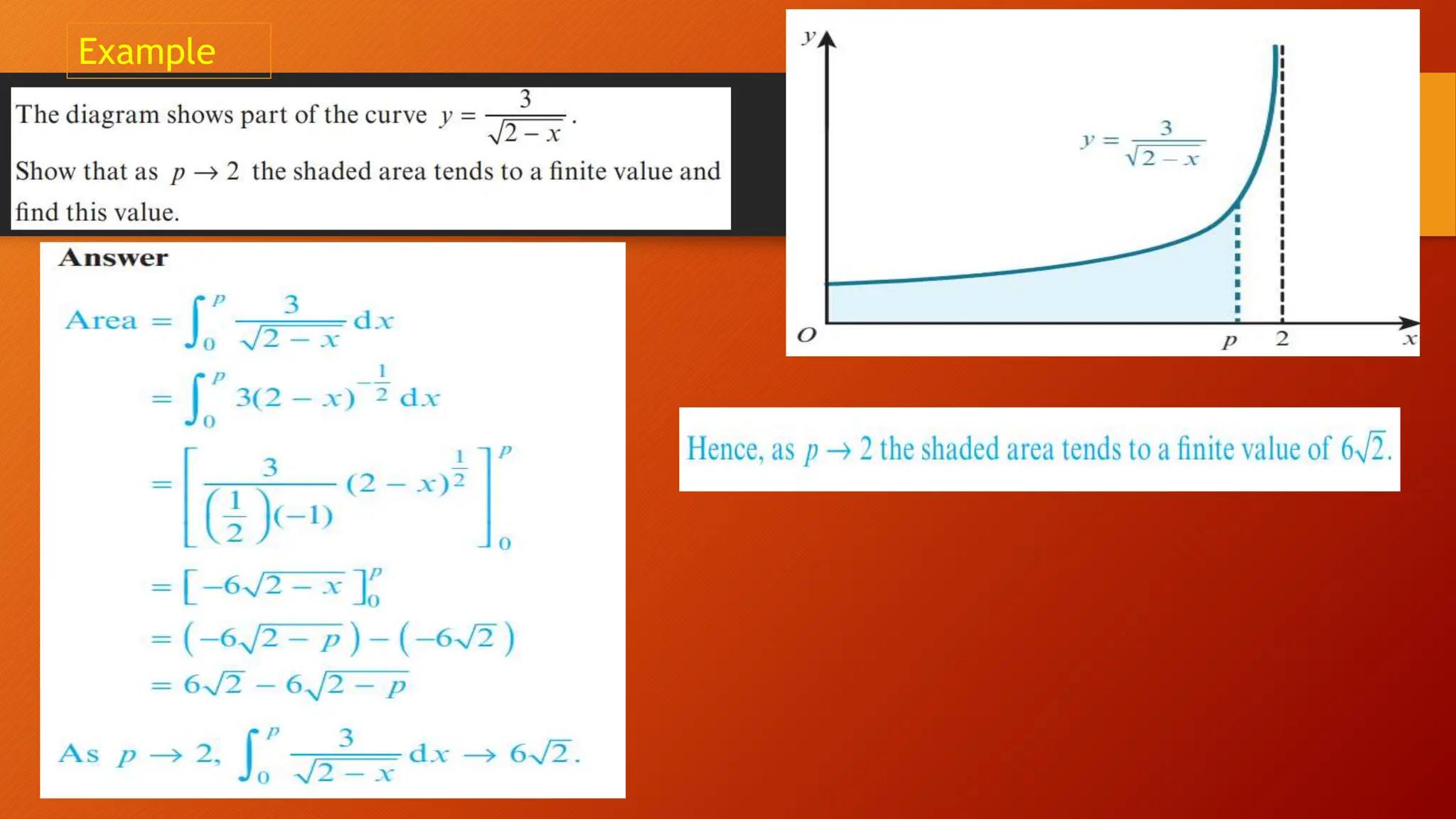
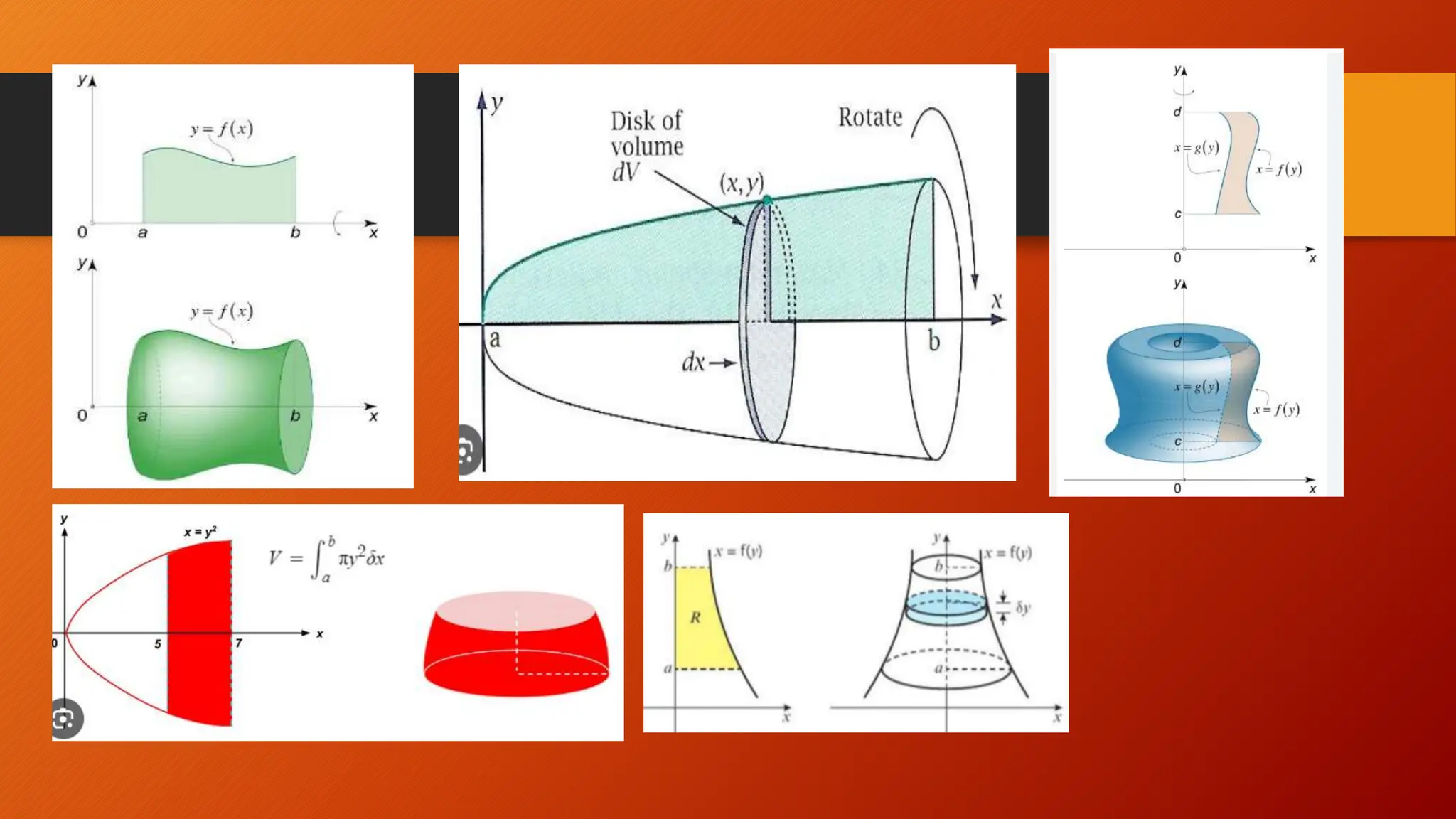
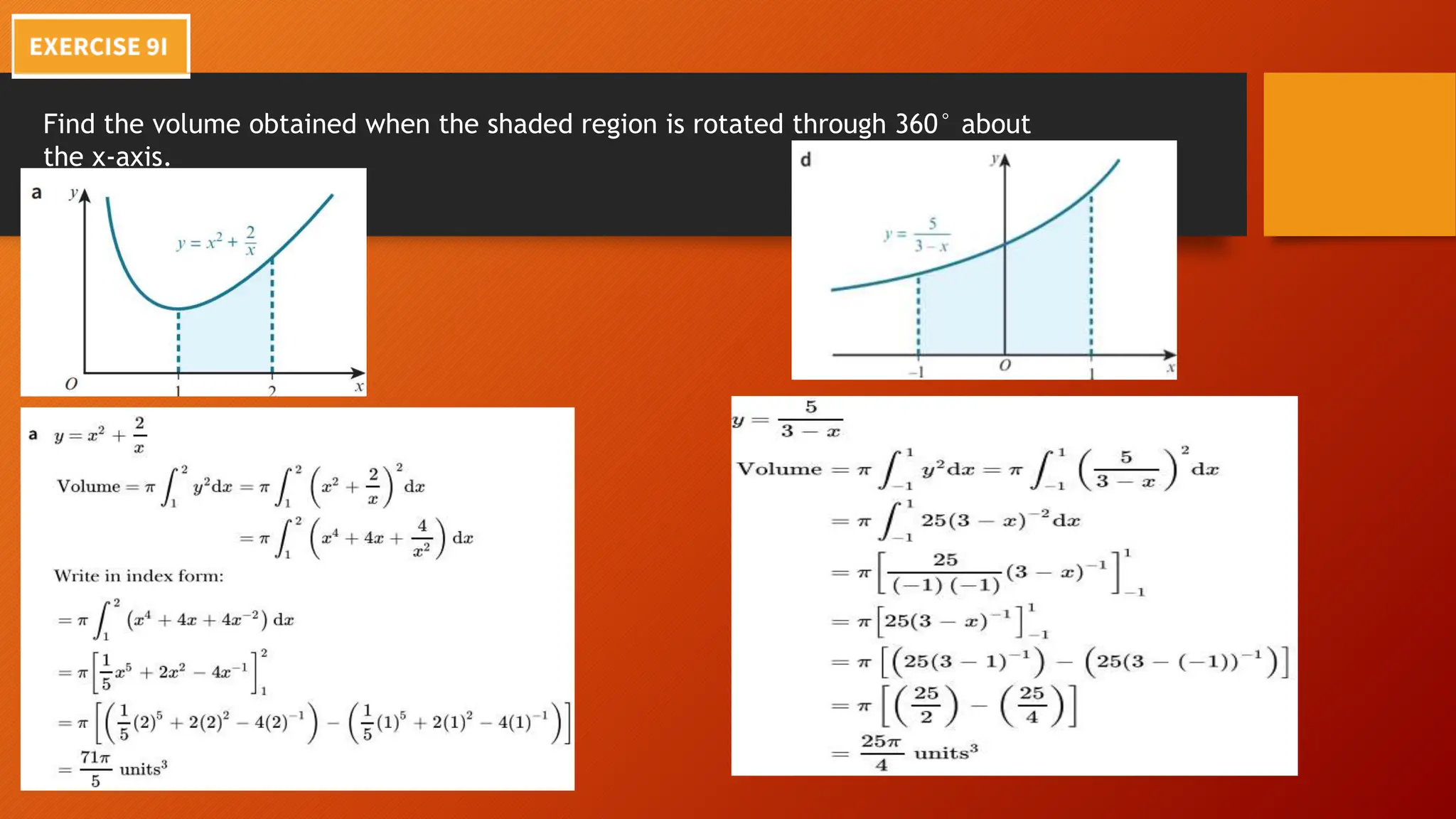
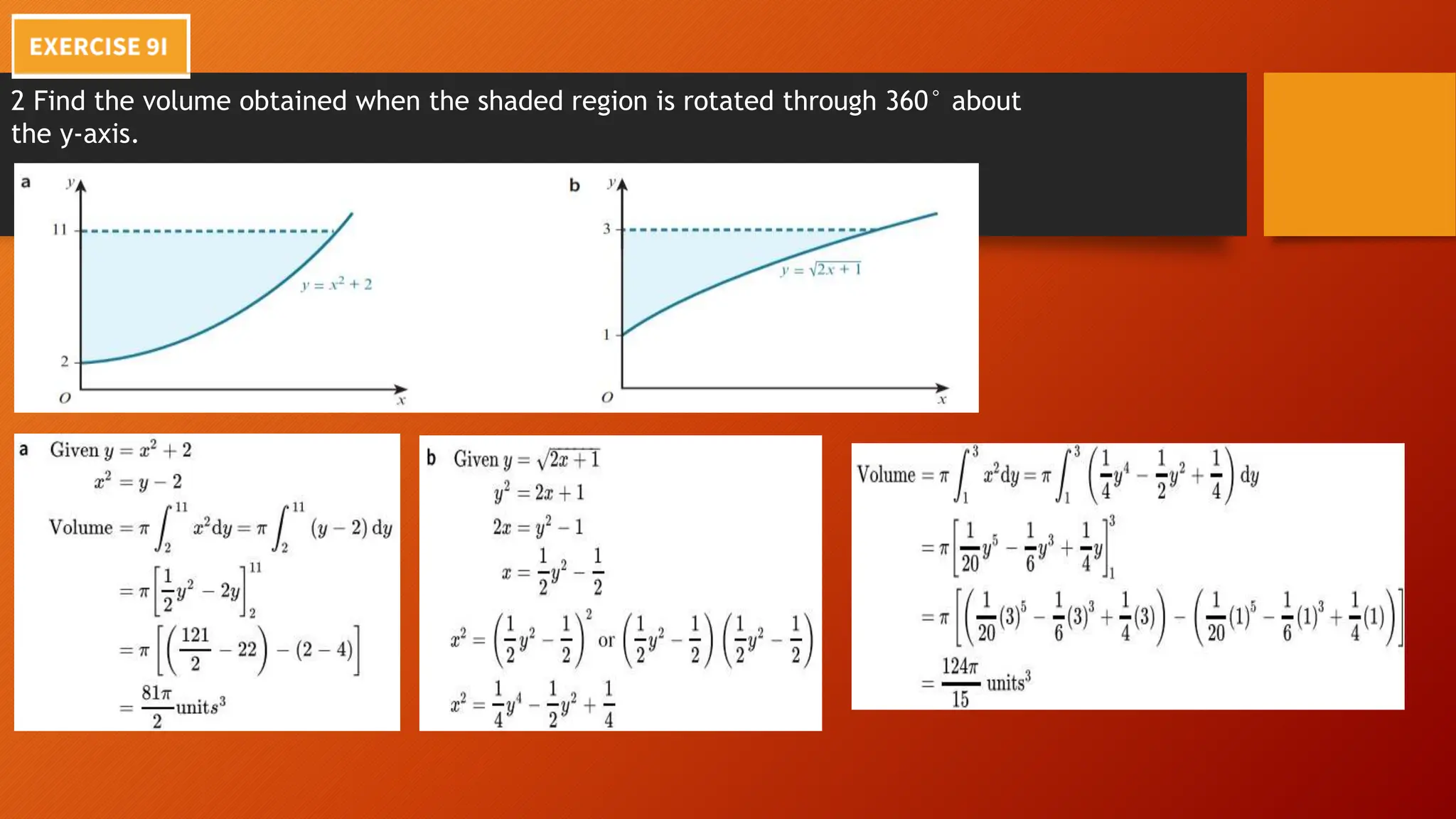
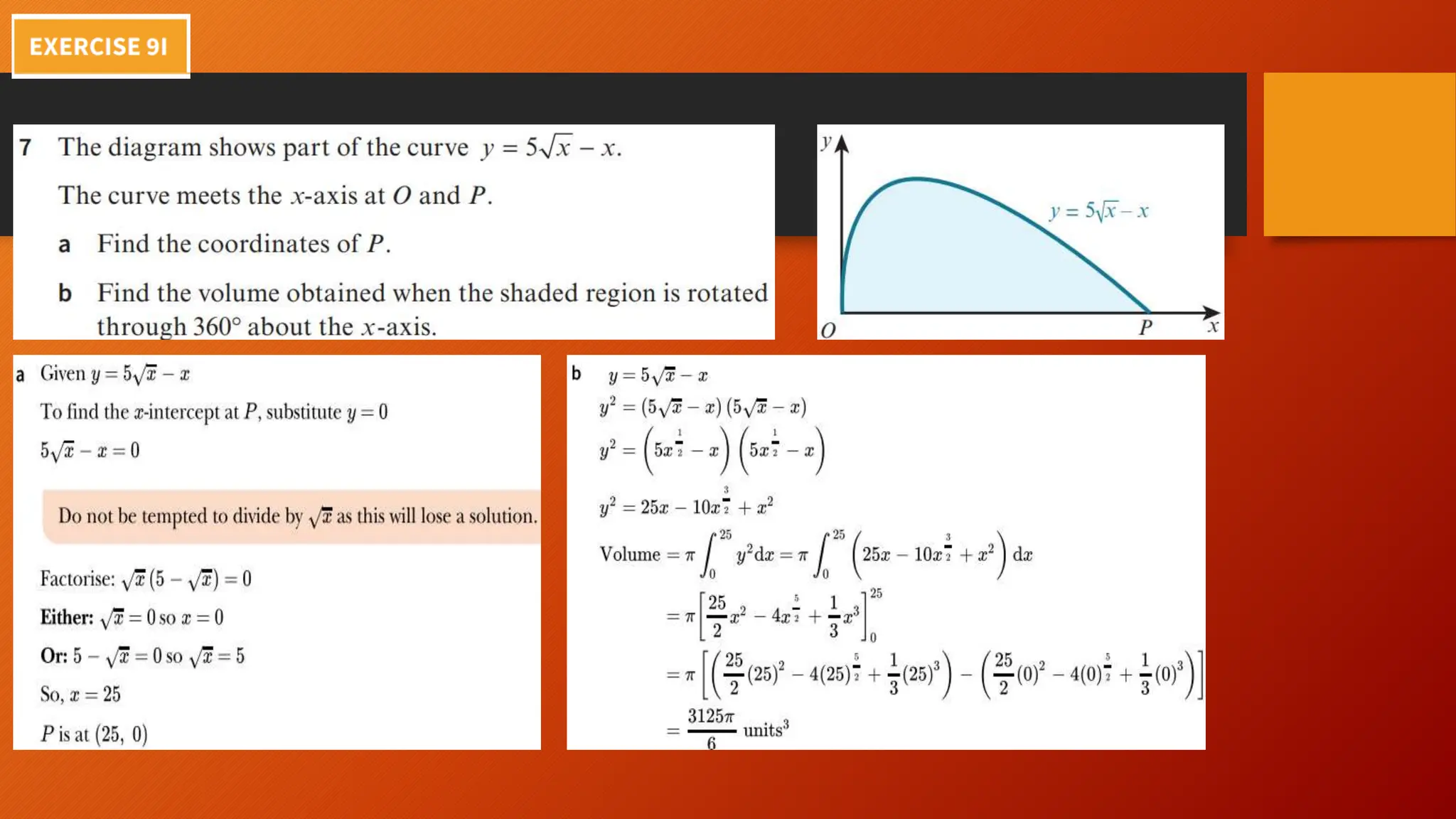
This document discusses the relationship between integration and differentiation in calculus, explaining that they are inverse operations. Differentiation measures how a function's output changes with respect to input, while integration finds the accumulated effect of these changes over an interval. The document also touches on improper integrals and solids of revolution in relation to these concepts.

1. INTEGRATION
CHAPTER 9

2. Why the Integration is inverse of
differentiation?
Integration and differentiation are two
fundamental operations in calculus that are
related to each other in a very important way.
Differentiation is the process of finding the rate
at which a quantity changes. It measures how a
function's output changes as its input changes.
Geometrically, differentiation gives the slope of
the tangent line to the curve representing the
function at any given point.
Integration, on the other hand, is essentially the
opposite process. It is used to find the
accumulated effect of a rate of change over a
given interval. It calculates the area under the
curve of a function between two points.
This theorem essentially tells us that integration and differentiation are
inverse operations of each other. When we differentiate a function f(x), we
are essentially finding the rate of change of some quantity represented by
that function. When we integrate the result of differentiation, we're finding
the accumulation of those changes, which brings us back to the original
quantity.
So, in summary, integration and differentiation are inverse operations
because they essentially "undo" each other. Differentiation measures the
rate of change, while integration computes the

3. Why the Integration is inverse of
differentiation?

9. Example

12. Example

13. Example

20. If two functions, f(x) and g( x) , intersect at
x =a and x =b , then the area, A, enclosed
between the two curves is given by

23. In this section, we will consider what happens if some part of a definite
integral becomes infinite. These are known as improper integrals, and we
will look at two different types.
These are definite integrals that have either one limit
infinite or both limits infinite
Type 1

24. Example

26. Type 2
These are integrals where the function to be integrated
approaches an infinite value (or approaches ± infinity) at
either or both end points in the interval (of integration)

27. Example

28. Show that each of the following improper integrals has a finite value and, in each case, find
this value

30. 3 Show that none of the following improper integrals exists

33. If a region in a plane is revolved around a line in that plane, the resulting
solid is called a solid of revolution, as shown in the following figure.

34. Example

35. Find the volume obtained when the shaded region is rotated through 360° about
the x-axis.

36. 2 Find the volume obtained when the shaded region is rotated through 360° about
the y-axis.