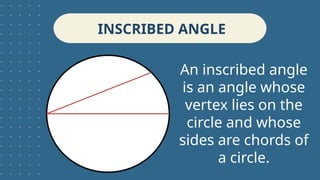
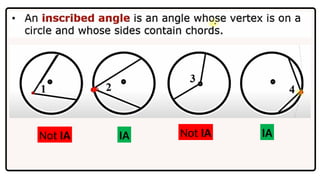
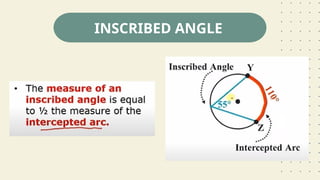
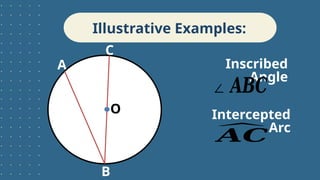
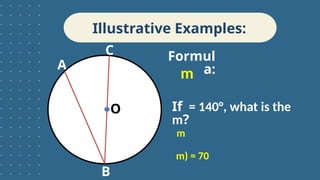
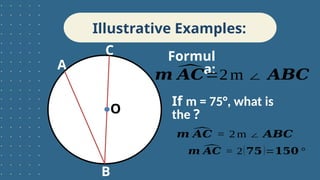
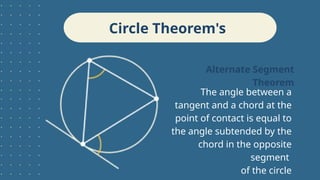
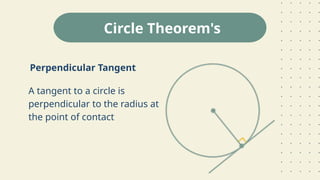
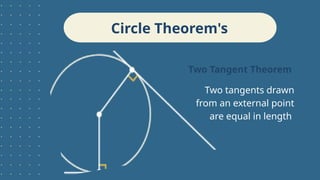
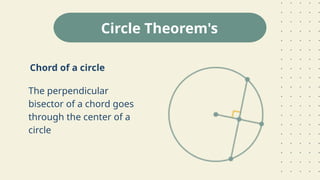
The document outlines learning objectives related to inscribed angles and intercepted arcs, including definitions, relationships, and methods for finding measures. It explains the concept of an inscribed angle and includes examples and formulas. Additionally, it covers several circle theorems, such as the perpendicular tangent theorem and properties of tangents and chords.

1. INSCRIBED ANGLES
and INTERCEPTED
ARCS

2. Learning Objectives:
• Define and illustrate
inscribed angles.
• Determine the relationship
between an inscribed
angle and its intercepted
arc.
• Find measures of inscribed
angles.

3. INSCRIBED ANGLE
An inscribed angle
is an angle whose
vertex lies on the
circle and whose
sides are chords of
a circle.

4. Not IA Not IA
IA IA

5. INSCRIBED ANGLE

6. A
Illustrative Examples:
B
C
O
Inscribed
Angle
∠ 𝑨𝑩𝑪
Intercepted
Arc
^
𝑨𝑪

7. A
Illustrative Examples:
B
C
O
Formul
a:
m
If = 140°, what is the
m?
m
m) = 70

8. A
Illustrative Examples:
B
C
O
Formul
a:
𝒎 ^
𝑨𝑪=2m ∠ 𝑨𝑩𝑪
If m = 75°, what is
the ?
𝒎 ^
𝑨𝑪 = 2 m ∠ 𝑨𝑩𝑪
𝒎 ^
𝑨𝑪 = 2(𝟕𝟓)=𝟏𝟓𝟎 °

9. A. Name all the inscribed
angles and their
corresponding intercepted
arcs.
CLASS ACTIVITY
Inscribed Angle Intercepted Arcs

10. Alternate Segment
Theorem
The angle between a
tangent and a chord at the
point of contact is equal to
the angle subtended by the
chord in the opposite
segment
of the circle
Circle Theorem's

11. Perpendicular Tangent
A tangent to a circle is
perpendicular to the radius at
the point of contact
Circle Theorem's

12. Two Tangent Theorem
Two tangents drawn
from an external point
are equal in length
Circle Theorem's

13. Chord of a circle
The perpendicular
bisector of a chord goes
through the center of a
circle
Circle Theorem's

14. Thank you for
listening!