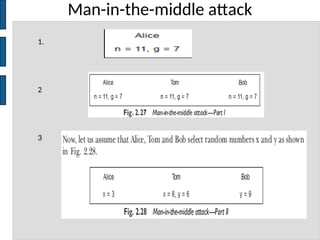
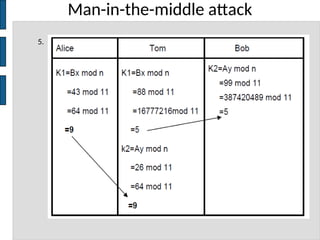
The document discusses key concepts in public key cryptography, including prime numbers, Euclid's algorithm, modular arithmetic, and the Diffie-Hellman key exchange algorithm. It explains the basis of public key algorithms in modular arithmetic and details the processes of key generation and agreement, along with potential vulnerabilities like the man-in-the-middle attack. Additionally, it compares symmetric and asymmetric encryption methods and introduces digital signatures and envelopes.

1. Public Key Cryptography
Prime Numbers
Euclid’s algorithm
Modular Arithmetic & Discrete Logarithms
Diffie-Hellman Key Exchange Algorithm
RSA algorithm
Symmetric vs Asymmetric
Digital Envelopes
Digital Signatures

2. PRIME NUMBERS
Prime number
a positive integer greater than 1, whose only
factors are 1 and itself.
cannot be divided by any number other than 1
and itself.
Ex:- 2,3,5,7,11,… Prime numbers
Relatively Prime
Two numbers are relatively prime when they
have no factors in common other than 1.
Ex:- gcd(21,44)=1 //21 & 44 are relatively prime
Ex:- gcd(21,45)// common factor is 3

3. Euclid’s Algorithm
Euclid’s Algorithm
A method to calculate GCD of two numbers.
Ex:- Trace the algorithm for x=21 and y=45
Table A.I Trace of the Euclid’s Algorithm
x y a
21 45 NA
3 21 21
0 3 3

4. Euclid’s Algorithm in C Language

5. Modular Arithmetic
• Most of the public key algorithms are based
on modular arithmetic.
• Modular Arithmetic uses non-negative
integers less than some positive integer n ,
performs ordinary arithmetic operations such
as addition, multiplication, and then replaces
the result with its remainder when divided by
n.
• When we write “x mod n”, we mean the
remainder of x when divided by n.

6. Modular Arithmetic
Modulo is the remainder left after an integer
division.
Ex:- 23 mod 11= 1 // 1 is remainder of 23/11
Modular arithmetic says that 23 & 11 are equivalent.
That is , 23 11(mod 1)
 The triple equal sign denotes congruence.

7. Modular Arithmetic
Examples:-
Mod 10 addition:- 3+5=8
7+6=13 =>3
5+5=10=>0
Mod 10 multiplication:- 3*2=6
5*5=25 =>5
7*6=42 =>2
Mod 10 exponentiation: x y
mod n
53
mod 10= 125 mod
10=>5

8. Diffie-Hellman Key
Exchange/Agreement Algorithm
• Key Exchange problem is solved in 1976 by
Diffie and Hellman
• The solution is called Diffie-Hellman Key
Exchange/Agreement Algorithm.
• Two parties who want to communicate
securely, can agree on a symmetric key using
this technique.
• This algorithm only used to key agreement,
but not for encryption or decryption.

9. Diffie-Hellman key exchange algorithm

10. Mathematical theory behind the
algorithm

11. Example of Diffie-Hellman Exchange

12. Problems with the algorithm
• Diffie-Hellman key exchange algorithm
– Can fall pray to the
– man-in-the-middle attack (or)
woman-in-the-middle-attack, (or)
bucket brigade attack.

13. Man-in-the-middle attack
1.
2
3

14. Man-in-the-middle attack
4.

15. Man-in-the-middle attack
5.