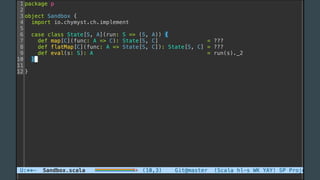
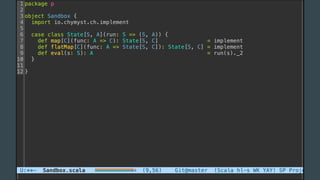
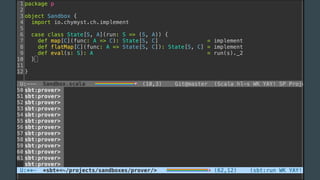
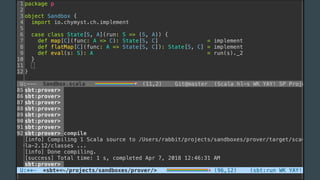
The document discusses the history of software engineering and early ideas in the field. It notes that the term "software engineering" was coined in 1968 to imply a more rigorous, engineering-based approach was needed for software development. Early conferences discussed ideas like integrating testing into design instead of after, and that small teams tend to be more successful than large ones. The document also examines some of the challenges faced and lessons learned over decades of software development.






























































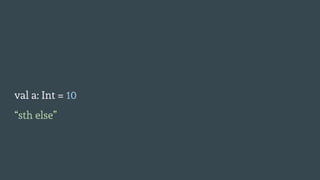

![trait Eq[A] {
def ===(a1: A)(a2: A): Boolean
}
val a: Int = 10
if(a == “10”) “ten” else “sth else”](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-66-320.jpg)
![trait Eq[A] {
def ===(a1: A)(a2: A): Boolean
}
val a: Int = 10
if(a === “10”) “ten” else “sth else”](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-67-320.jpg)
![trait Eq[A] {
def ===(a1: A)(a2: A): Boolean
}
val a: Int = 10
if(a === “10”) “ten” else “sth else”
Doesn’t
compile](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-68-320.jpg)
![trait Eq[A] {
def ===(a1: A)(a2: A): Boolean
}
val a: Int = 10
if(a === “10”) “ten” else “sth else”
Doesn’t
compile
and that’s a goodthing!](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-69-320.jpg)


![/** Concatenate two maps. Keys from both maps must be
* included. If keys collide, add values together. */
def concat(
map1: Map[String, Int],
map2: Map[String, Int]
): Map[String, Int] = ???](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-72-320.jpg)





![/** Concatenate two maps. Keys from both maps must be
* included. If keys collide, add values together. */
def concat(
map1: Map[String, Int],
map2: Map[String, Int]
): Map[String, Int] = ???](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-78-320.jpg)
![/** Concatenate two maps. Keys from both maps must be
* included. If keys collide, add values together. */
def concat(
map1: Map[String, Option[(Int, Option[FinancialReport])],
map2: Map[String, Option[(Int, Option[FinancialReport])]
): Map[String, Option[(Int, Option[FinancialReport])] = ???](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-79-320.jpg)




![trait Semigroup[A] {
def |+|(a1: A, a2: A): A
}](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-84-320.jpg)
![trait Semigroup[A] {
def |+|(a1: A, a2: A): A
}
trait Semigroup {
def pairS[A, B]: Semigroup[(A, B)] = ???
}](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-85-320.jpg)
![trait Semigroup[A] {
def |+|(a1: A, a2: A): A
}
trait Semigroup {
def pairS[A:Semigroup, B:Semigroup]: Semigroup[(A, B)] = ...
}](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-86-320.jpg)
![trait Semigroup[A] {
def |+|(a1: A, a2: A): A
}
trait Semigroup {
def pairS[A:Semigroup, B:Semigroup]: Semigroup[(A, B)] = ...
def optionS[A:Semigroup]: Semigroup[Option[A]] = ...
}](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-87-320.jpg)
![trait Semigroup[A] {
def |+|(a1: A, a2: A): A
}
trait Semigroup {
def pairS[A:Semigroup, B:Semigroup]: Semigroup[(A, B)] = ...
def optionS[A:Semigroup]: Semigroup[Option[A]] = ...
def mapS[A, B:Semigroup]: Semigroup[Map[A,B]] = ...
}](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-88-320.jpg)
![/** Concatenate two maps. Keys from both maps must be
* included. If keys collide, add values together. */
def concat(
m1: Map[String, Option[(Int, Option[FinancialReport])],
m2: Map[String, Option[(Int, Option[FinancialReport])]
): Map[String, Option[(Int, Option[FinancialReport])] = ???](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-89-320.jpg)
![/** Concatenate two maps. Keys from both maps must be
* included. If keys collide, add values together. */
def concat(
m1: Map[String, Option[(Int, Option[FinancialReport])],
m2: Map[String, Option[(Int, Option[FinancialReport])]
): Map[String, Option[(Int, Option[FinancialReport])] = m1 |+| m2](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-90-320.jpg)



















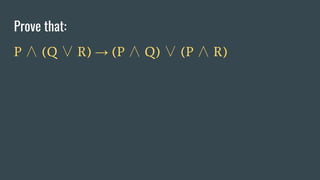

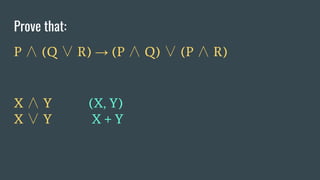
![Prove that:
P ∧ (Q ∨ R) → (P ∧ Q) ∨ (P ∧ R)
X ∧ Y (X, Y)
X ∨ Y Either[X, Y]](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-113-320.jpg)
![Prove that:
P ∧ (Q ∨ R) → (P ∧ Q) ∨ (P ∧ R)
X ∧ Y (X, Y)
X ∨ Y Either[X, Y]
X → Y X => Y](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-114-320.jpg)
![Prove that:
P ∧ (Q ∨ R) → (P ∧ Q) ∨ (P ∧ R)
def proof[P, Q, R]: (P, Either[Q, R]) => Either[(P, Q), (P, R)] = ???](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-115-320.jpg)
![Prove that:
P ∧ (Q ∨ R) → (P ∧ Q) ∨ (P ∧ R)
def proof[P, Q, R]: (P, Either[Q, R]) => Either[(P, Q), (P, R)] = ???](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-116-320.jpg)
![Prove that:
P ∧ (Q ∨ R) → (P ∧ Q) ∨ (P ∧ R)
def proof[P, Q, R]: (P, Either[Q, R]) => Either[(P, Q), (P, R)] = ???](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-117-320.jpg)
![Prove that:
P ∧ (Q ∨ R) → (P ∧ Q) ∨ (P ∧ R)
def proof[P, Q, R]: (P, Either[Q, R]) => Either[(P, Q), (P, R)] =
(input: (P, Either[Q, R])) => input match {
case (p, Left(q)) => Left((p, q))
case (p, Right(r)) => Right((p, r))
}](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-118-320.jpg)
![Prove that:
P ∧ (Q ∨ R) → (P ∧ Q) ∨ (P ∧ R)
def proof[P, Q, R]: (P, Either[Q, R]) => Either[(P, Q), (P, R)] =
(input: (P, Either[Q, R])) => input match {
case (p, Left(q)) => Left((p, q))
case (p, Right(r)) => Right((p, r))
}](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-119-320.jpg)



![So why can’t we prove?
P ∨ ¬P
¬P P => Nothing
def proof[P]: Either[P, P => Nothing] = ???](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-123-320.jpg)












: A = a](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-136-320.jpg)
![def willProveAnything[A]: A = ???](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-137-320.jpg)
![def willProveAnything[A]: A = null](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-138-320.jpg)
![def willProveAnything[A]: A = throw RuntimeException(“ha!”)](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-139-320.jpg)
![def willProveAnything[A]: A = willProveAnything](https://image.slidesharecdn.com/illogicalengineers-180906084301/85/Illogical-engineers-140-320.jpg)