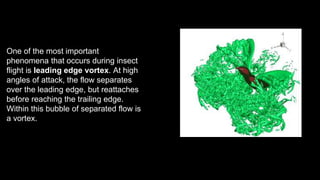
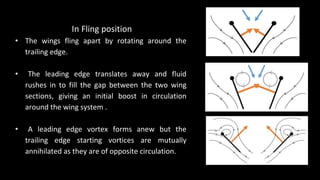
This document discusses how hummingbirds fly by flapping their wings through downstrokes and upstrokes. It explains that early theories assumed steady airflow over flapping wings, but researchers realized unsteady phenomena must provide aerodynamic forces since calculated lift was too small. A key phenomenon is leading edge vortices at high angles of attack that transfer momentum downward, creating more lift and drag. The document also discusses equations governing insect flight, hovering through rapid wing flapping, and the clap-and-fling mechanism where wings clap together then fling apart to boost circulation.

1. How do
Hummingbird
Fly?

2. Flapping wings
move through
two basic half-
strokes

3. The downstroke starts up and back
and is plunged downward and forward.
Then the wing is quickly
flipped over (supination)
so that the leading edge
is pointed backward.

4. The upstroke then pushes the wing upward
and backward. Then the wing
is flipped again (pronation)
and another downstroke
can occur.

5. The first attempts to understand flapping
wings assumed a quasi-steady state.
This means that the air flow
over the wing at any given
time was assumed to
be the same as how
the flow would
be over a non-flapping,
steady-state wing at
the same angle of attack.

6. By dividing the flapping wing into a large number
of motionless positions and then analyzing
each position, it would be possible
to create a timeline of the
instantaneous forces on the
wing at every moment.
The calculated lift was found
to be too small by a factor
of three, so researchers realized
that there must be unsteady
phenomena providing
aerodynamic forces.

7. The aerodynamic theory for
airplanes doesn’t work so
well in predicting the force
of lift for flapping wings

8. One of the most important
phenomena that occurs during insect
flight is leading edge vortex. At high
angles of attack, the flow separates
over the leading edge, but reattaches
before reaching the trailing edge.
Within this bubble of separated flow is
a vortex.

10. Because the angle of
attack is so high, a lot of
momentum is transferred
downward into the flow.
These two features create
a large amount of lift force
as well as some additional
drag.

13. Equations governing the Insect Flight:
Just like aircraft wings insect wings also experience fluid forces when moving through
air. The force that acts normal to the direction of flow relative to wing is called lift and the
force that acts along the direction of flow relative to wing is known as drag.
Dynamic pressure: ½(ρU^2)
Area of Wing: S
Therefore, unit of force: Dynamic Pressure * Area of Wing => ½(ρU^2*S)
Coefficient of lift(CL) and drag(CD):
CL(α) = 2L/(ρU^2*S) and CD(α) =
2D/(ρU^2*S)

14. ● CL and CD are constant in case of steady flow which happens when a special kind
of airfoil moves through a fluid at low angle attack.
● The corresponding lift is given by Bernoulli's principle:
CL = 2π sin(α) and CD = 0
● The flow around insect wings can be considered incompressible because of very
low mach number of around 1/300. Hence the governing equation is the Navier-
Stokes equation subject to no-slip boundary condition:
∂u/∂t + (u · ∇)u = −∇ p/ρ + ν∇2
u, (1)
∇ · u = 0,
(2)
ubd = us
(3)
● u(x,t)= Flow field , p= Pressure, ρ= Density of the fluid, ν= Kinematic viscosity,
ubd= Velocity at boundary layer, us= Velocity of the solid

15. Hovering in Insects:
● Insects can hover by flapping their wings rapidly resulting in sideways
stabilization as well as production of lift.
● We can calculate typical wing beat frequency necessary to maintain hover flight
by assuming constant lift in downstroke and zero lift in upstroke.
● During the time interval Δt of the upward wingbeat, the insect drops a distance h
under the influence of gravity: h = gΔt2/2
● Assuming insect’s vertical position does not changes by more than 0.1 mm,
maximum allowable free fall time: Δt = (2h/g)½ ~ 4.5*10-3
● Hence total period T as up and down movements take equal time = 9 *10-3
● Frequency = 1/T = 110Hz

16. Clap and Fling Mechanism
The clap-and-fling mechanism was first proposed
by Weis-Fogh (1973) to explain the high lift
generation and is sometimes also referred to as the
Weis-Fogh mechanism.

17. CFSection schematic of wings
approaching each other to clap.
Black lines show flow lines, and
dark blue arrows show induced
velocity.
Light blue arrows show net forces
acting on the airfoil.

18. Starting from the clap position
• •As the wings approach each other dorsally, their
leading edges touch initially and the wing rotates
around the leading edge.
• •Vorticity shed from the trailing edge rolls up in the
form of stopping vortices which dissipate into the
wake.
• •The leading edge vortices also lose strength. The
closing gap between the two wings pushes fluid
out, giving an additional thrust.

19. cdddddddDDIn Fling position
• The wings fling apart by rotating around the
trailing edge.
• •The leading edge translates away and fluid
rushes in to fill the gap between the two wing
sections, giving an initial boost in circulation
around the wing system .
• •A leading edge vortex forms anew but the
trailing edge starting vortices are mutually
annihilated as they are of opposite circulation.

20. Thankyou
Meet Our Group
Susanket Sarkar
Jagteshvar Singh Sahni
Aditya Kaushal
Rohit kumar
Mohd Gufran Ansari