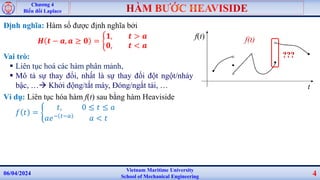
Tài liệu trình bày về biến đổi Laplace trong lĩnh vực kỹ thuật cơ khí, bao gồm định nghĩa và ứng dụng của hàm Heaviside để liên tục hóa các hàm phân mảnh. Nó cũng cung cấp các ví dụ giải phương trình vi phân bằng biến đổi Laplace và thảo luận về điều kiện đầu và ảnh hưởng của chúng trong giải pháp. Các phép biến đổi Laplace này được sử dụng để khảo sát động lực học của hệ thống trong miền tần số và trở về miền thời gian thực.

1. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 1
Chương 4
Biến đổi Laplace
1. Biến đổi Laplace
Xét hàm phân mảnh (liên tục từng đoạn) 𝑓(𝑡): 𝑓 𝑡 = 0
với 𝑡 < 0.
Biến đổi Laplace của 𝑓(𝑡) được định nghĩa bởi tích
phân:
𝑭 𝒔 = 𝑳 𝒇 𝒕 =
𝟎
∞
𝒇 𝒕 𝒆−𝒔𝒕𝒅𝒕
2. Biến đổi Laplace ngược
Biến đổi Laplace ngược của 𝐹(𝑠) được định nghĩa bởi
tích phân:
𝒇 𝒕 = 𝑳−𝟏{𝑭 𝒔 }
Mục đích: Trả lại kết quả khảo sát đặc tính động lực của
cơ hệ trong miền tần số 𝒔 về miền thời gian thực 𝒕, nhằm
thực hiện quá trình điều khiển/điều chỉnh cơ hệ.
f(t)
L-1{F(s)}
t s
F(s)
t s

2. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 2
Chương 4
Biến đổi Laplace
Ví dụ 1: Giải phương trình vi phân sau bằng biến đổi Laplace
𝑦′′ + 3𝑦′ + 2𝑦 = 𝑓 𝑡 , 𝑦 0 = 0, 𝑦′ 0 = 1.
Trong đó:
𝑓 𝑡 =
𝑡, 0 < 𝑡 < 1
0, 1 < 𝑡
Giải như thế nào?  Hàm bước Heaviside.

3. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 3
Chương 4
Biến đổi Laplace
f(t)
t
f(t)
Định nghĩa: Hàm số được định nghĩa bởi
𝑯 𝒕 − 𝒂, 𝒂 ≥ 𝟎 =
𝟏, 𝒕 > 𝒂
𝟎, 𝒕 < 𝒂
Vai trò:
 Liên tục hoá các hàm phân mảnh,
 Mô tả sự thay đổi, nhất là sự thay đổi đột ngột/nhảy
bậc, … Khởi động/tắt máy, Đóng/ngắt tải, …
Ví dụ:
Hàm 𝑓 𝑡 = 𝑔(𝑡) 𝐻 𝑡 − 𝑎 − 𝐻(𝑡 − 𝑏) mô tả hàm
phân mảnh sau:
𝑓 𝑡 =
0 𝑡 < 𝑎
𝑔 𝑡 𝑎 < 𝑡 < 𝑏
0 𝑡 > 𝑏
???
Hàm Heaviside step function
t
g(t)
a b
0

4. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 4
Chương 4
Biến đổi Laplace
f(t)
t
f(t)
Định nghĩa: Hàm số được định nghĩa bởi
𝑯 𝒕 − 𝒂, 𝒂 ≥ 𝟎 =
𝟏, 𝒕 > 𝒂
𝟎, 𝒕 < 𝒂
Vai trò:
 Liên tục hoá các hàm phân mảnh,
 Mô tả sự thay đổi, nhất là sự thay đổi đột ngột/nhảy
bậc, … Khởi động/tắt máy, Đóng/ngắt tải, …
Ví dụ: Liên tục hóa hàm f(t) sau bằng hàm Heaviside
𝑓 𝑡 =
𝑡, 0 ≤ 𝑡 ≤ 𝑎
𝑎𝑒− 𝑡−𝑎 𝑎 < 𝑡
???

5. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 5
Chương 4
Biến đổi Laplace
Định nghĩa: Hàm số được định nghĩa bởi
𝑯 𝒕 − 𝒂, 𝒂 ≥ 𝟎 =
𝟏, 𝒕 > 𝒂
𝟎, 𝒕 < 𝒂
Vai trò:
 Liên tục hoá các hàm phân mảnh,
 Mô tả sự thay đổi, nhất là sự thay đổi đột ngột/nhảy
bậc, … Khởi động/tắt máy, Đóng/ngắt tải, …
Ví dụ: Liên tục hóa hàm f(t) sau bằng hàm Heaviside
𝑓 𝑡 =
𝑓1(𝑡), 𝑡 < 𝑡0
0, 𝑡0 < 𝑡
→ 𝑓 𝑡 = 𝑓1 𝑡 1 − 𝐻(𝑡 − 𝑡0)
t
t0
0
f(t)
f1(t)

6. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 6
Chương 4
Biến đổi Laplace
Định nghĩa: Hàm số được định nghĩa bởi
𝑯 𝒕 − 𝒂, 𝒂 ≥ 𝟎 =
𝟏, 𝒕 > 𝒂
𝟎, 𝒕 < 𝒂
Vai trò:
 Liên tục hoá các hàm phân mảnh,
 Mô tả sự thay đổi, nhất là sự thay đổi đột ngột/nhảy
bậc, … Khởi động/tắt máy, Đóng/ngắt tải, …
Ví dụ: Liên tục hóa hàm f(t) sau bằng hàm Heaviside
𝑓 𝑡 =
0, 𝑡 < 𝑡0
𝑓2(𝑡), 𝑡0 < 𝑡
→ 𝑓 𝑡 = 𝑓2 𝑡 𝐻(𝑡 − 𝑡0)
t
t0
0
f(t)
f2(t)

7. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 7
Chương 4
Biến đổi Laplace
Định nghĩa: Hàm số được định nghĩa bởi
𝑯 𝒕 − 𝒂, 𝒂 ≥ 𝟎 =
𝟏, 𝒕 > 𝒂
𝟎, 𝒕 < 𝒂
Vai trò:
 Liên tục hoá các hàm phân mảnh,
 Mô tả sự thay đổi, nhất là sự thay đổi đột ngột/nhảy
bậc, … Khởi động/tắt máy, Đóng/ngắt tải, …
Ví dụ: Liên tục hóa hàm f(t) sau bằng hàm Heaviside
𝑓 𝑡 =
𝑓1(𝑡), 𝑡 < 𝑡0
𝑓2(𝑡), 𝑡0 < 𝑡
→ 𝑓 𝑡 = 𝑓1 𝑡 1 − 𝐻(𝑡 − 𝑡0) + 𝑓2 𝑡 𝐻(𝑡 − 𝑡0)
t
t0
0
f(t)
f1(t)
f2(t)

8. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 8
Chương 4
Biến đổi Laplace
Định nghĩa: Hàm số được định nghĩa bởi
𝑯 𝒕 − 𝒂, 𝒂 ≥ 𝟎 =
𝟏, 𝒕 > 𝒂
𝟎, 𝒕 < 𝒂
Vai trò:
 Liên tục hoá các hàm phân mảnh,
 Mô tả sự thay đổi, nhất là sự thay đổi đột ngột/nhảy
bậc, … Khởi động/tắt máy, Đóng/ngắt tải, …
Ví dụ: Liên tục hóa hàm f(t) sau bằng hàm Heaviside
𝑓 𝑡 =
𝑡, 0 ≤ 𝑡 ≤ 𝑎
𝑎𝑒− 𝑡−𝑎 𝑎 < 𝑡
→ 𝑓 𝑡 =
𝑓1 𝑡 = 𝑡, 0 ≤ 𝑡 ≤ 𝑎
𝑓2 𝑡 = 𝑎𝑒− 𝑡−𝑎 𝑎 < 𝑡
t
a
0
f(t)

9. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 9
Chương 4
Biến đổi Laplace
Định nghĩa: Hàm số được định nghĩa bởi
𝑯 𝒕 − 𝒂, 𝒂 ≥ 𝟎 =
𝟏, 𝒕 > 𝒂
𝟎, 𝒕 < 𝒂
Ví dụ: Liên tục hóa hàm f(t) sau bằng hàm Heaviside
𝑓 𝑡 =
𝑓1 𝑡 = 0 𝑡 < 0
𝑓2 𝑡 = 𝑡 0 ≤ 𝑡 ≤ 𝑎
𝑓3 𝑡 = 𝑎𝑒− 𝑡−𝑎 𝑎 < 𝑡
Tại t0 = a:
𝑓 𝑡 =
𝑓1 𝑡 = 𝑡 𝑡 < 𝑎
𝑓2 𝑡 = 𝑎𝑒− 𝑡−𝑎 𝑡 > 𝑎
→ 𝑓 𝑡 = 𝑓1 𝑡 1 − 𝐻(𝑡 − 𝑡0) + 𝑓2 𝑡 𝐻 𝑡 − 𝑡0
= 𝑡 1 − 𝐻 𝑡 − 𝑎 + 𝑎𝑒− 𝑡−𝑎
𝐻 𝑡 − 𝑎
= 𝑡 − 𝑡𝐻 𝑡 − 𝑎 + 𝑎𝑒− 𝑡−𝑎 𝐻(𝑡 − 𝑎)
t
a
0
f(t)

10. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 10
Chương 4
Biến đổi Laplace
Định nghĩa: Hàm số được định nghĩa bởi
𝑯 𝒕 − 𝒂, 𝒂 ≥ 𝟎 =
𝟏, 𝒕 > 𝒂
𝟎, 𝒕 < 𝒂
Ví dụ: Liên tục hóa hàm f(t) sau bằng hàm Heaviside
𝑓 𝑡 =
𝑓1 𝑡 𝑡 < 𝑎
𝑓2 𝑡 𝑎 ≤ 𝑡 ≤ 𝑏
𝑓3 𝑡 𝑏 < 𝑡
Tại t0 = a:
𝑓 𝑡 =
𝑓1 𝑡 𝑡 < 𝑎
𝑓2 𝑡 𝑡 > 𝑎
→ 𝑓 𝑡 = 𝑓1 𝑡 1 − 𝐻(𝑡 − 𝑎) + 𝑓2 𝑡 𝐻 𝑡 − 𝑎
Tại t0 = b:
𝑓 𝑡 =
𝑓2 𝑡 𝑡 < 𝑏
𝑓3 𝑡 𝑡 > 𝑏
→ 𝑓 𝑡 = 𝑓2 𝑡 1 − 𝐻(𝑡 − 𝑏) + 𝑓3 𝑡 𝐻 𝑡 − 𝑏
⇒ 𝒇 𝒕 = 𝒇𝟏 𝒕 𝟏 − 𝑯(𝒕 − 𝒂) + 𝒇𝟐 𝒕 𝑯 𝒕 − 𝒂 − 𝒇𝟐 𝒕 𝑯(𝒕 − 𝒃) + 𝒇𝟑 𝒕 𝑯 𝒕 − 𝒃
t
a
0
f(t)

11. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 11
Chương 4
Biến đổi Laplace
f(t)
t
f(t)
Định nghĩa: Hàm số được định nghĩa bởi
𝑯 𝒕 − 𝒂, 𝒂 ≥ 𝟎 =
𝟏, 𝒕 > 𝒂
𝟎, 𝒕 < 𝒂
Vai trò:
 Liên tục hoá các hàm phân mảnh,
 Mô tả sự thay đổi, nhất là sự thay đổi đột ngột/nhảy
bậc, … Khởi động/tắt máy, Đóng/ngắt tải, …
Biến đổi Laplace:
𝑳 𝑯 𝒕 − 𝒂 =
𝒂
∞
𝒆−𝒔𝒕
𝒅𝒕 =
𝒆−𝒂𝒔
𝒔
, 𝒔 > 𝟎
⇒ 𝑳 𝒇(𝒕 − 𝒂)𝑯 𝒕 − 𝒂 = 𝒆−𝒂𝒔
𝑭 𝒔 , 𝒔 > 𝒂 ≥ 𝟎
Biến đổi Laplace bằng MATLAB:
H = heaviside(x);  Tìm hàm Heaviside của x
L = laplace(heaviside(x)); Tìm ảnh Laplace của
H(x)
???
Hàm Heaviside step function
t
f(t)
a b
0

12. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 12
Chương 4
Biến đổi Laplace
f(t)
t
f(t)
Định nghĩa: Hàm số được định nghĩa bởi
𝑯 𝒕 − 𝒂, 𝒂 ≥ 𝟎 =
𝟏, 𝒕 > 𝒂
𝟎, 𝒕 < 𝒂
Vai trò:
 Liên tục hoá các hàm phân mảnh,
 Mô tả sự thay đổi, nhất là sự thay đổi đột ngột/nhảy
bậc, … Khởi động/tắt máy, Đóng/ngắt tải, …
Biến đổi Laplace:
𝑳 𝑯 𝒕 − 𝒂 =
𝒂
∞
𝒆−𝒔𝒕
𝒅𝒕 =
𝒆−𝒂𝒔
𝒔
, 𝒔 > 𝟎
⇒ 𝑳 𝒇(𝒕 − 𝒂)𝑯 𝒕 − 𝒂 = 𝒆−𝒂𝒔
𝑭 𝒔 , 𝒔 > 𝒂 ≥ 𝟎
Ví dụ: Tìm biến đổi Laplace của hàm sau
𝑓 𝑡 = 𝑡2 + 2 𝐻 𝑡 − 1 + 𝐻(𝑡 − 2)
???
Hàm Heaviside step function
t
f(t)
a b
0

13. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 13
Chương 4
Biến đổi Laplace
Ví dụ 2: Giải PTVP sau bằng biến đổi Laplace
𝑦′′ + 3𝑦′ + 2𝑦 =
𝑡, 0 < 𝑡 < 1
0, 1 < 𝑡
Thỏa mãn điều kiện: 𝑦 0 = 𝑦′
0 = 0.

14. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 14
Chương 4
Biến đổi Laplace
Ví dụ 2: Giải PTVP sau bằng biến đổi Laplace
𝑦′′ + 3𝑦′ + 2𝑦 =
𝑡, 0 < 𝑡 < 1
0, 1 < 𝑡
Thỏa mãn điều kiện: 𝑦 0 = 𝑦′ 0 = 0.
Bài giải:
Bước 1: Xét Vế phải:
𝑓 𝑡 =
𝑡, 0 < 𝑡 < 1
0, 1 < 𝑡
↔ 𝑓 𝑡 =
𝑓1 𝑡 = 𝑡, 0 < 𝑡 < 1
𝑓2 𝑡 = 0, 1 < 𝑡
Bước 2: Áp dụng hàm Heaviside cho vế phải, ta có:
𝑓 𝑡 = 𝑓1 𝑡 1 − 𝐻(𝑡 − 1) + 𝑓2 𝑡 𝐻 𝑡 − 1 = 𝑡 − 𝑡𝐻 𝑡 − 1
= 𝑡 − 𝑡 − 1 𝐻 𝑡 − 1 − 𝐻(𝑡 − 1)
Bước 3: Áp dụng biến đổi Laplace cho cả 2 vế và giải phương trình.
t
1
0
f(t)
1
f1(t)
f2(t)

15. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 15
Chương 4
Biến đổi Laplace
Ví dụ: Giải PTVP sau bằng biến đổi Laplace:
𝑦′′ + 4𝑦′ = cos 𝑡 − 3 + 4𝑡, 𝑦 3 = 0, 𝑦′ 3 = 7.
Bài giải:
Điều kiện đầu:
𝑦 3 = 0
𝑦′
3 = 7
⇒
𝑦 0 = ?
𝑦′
0 = ?
Đặt: 𝑥 = 𝑡 − 3 → 𝑡 = 𝑥 + 3 → 𝑦′′
(𝑥 + 3) + 4𝑦′
(𝑥 + 3) = 𝑐𝑜𝑠(𝑥) + 4(𝑥 + 3)
Mặt khác:
𝑢 𝑥 = 𝑦 𝑥 + 3 → 𝑢′ 𝑥 =
𝑑𝑢
𝑑𝑥
=
𝑑𝑦
𝑑𝑡
𝑑𝑡
𝑑𝑥
= 𝑦′(𝑥 + 3)
𝑢′′
𝑥 = 𝑦′′
(𝑥 + 3)
𝑢(0) = 𝑦(0 + 3) = 𝑦(3) = 0
𝑢′(0) = 𝑦′(0 + 3) = 𝑦′(3) = 7
⇒ 𝑦 =
1
2
𝑡2
−
1
4
𝑡 −
43
16
−
273
272
𝑒−4 𝑡−3
+
1
17
(4 sin 𝑡 − 3 − cos(𝑡 − 3))

16. Vietnam Maritime University
School of Mechanical Engineering
06/04/2024 16
Chương 4
Biến đổi Laplace
Đề bài: Giải PTVP sau bằng biến đổi Laplace
𝑦′′
+ 3𝑦′
+ 2𝑦 =
𝑡, 0 < 𝑡 < 2
2𝑒− 𝑡−2
, 2 < 𝑡
Thỏa mãn điều kiện: 𝑦 0 = 𝑦′
0 = 0.