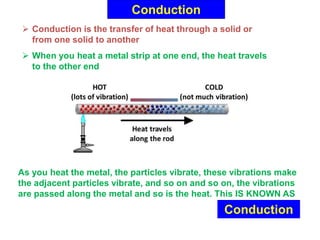
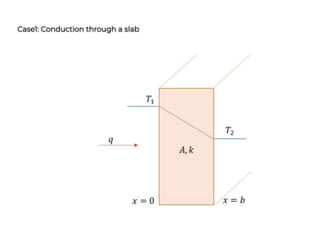
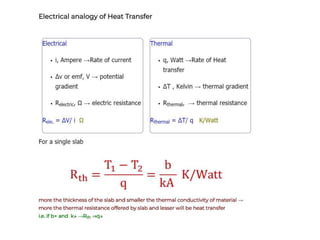
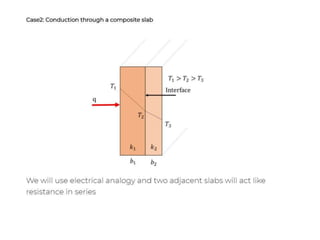
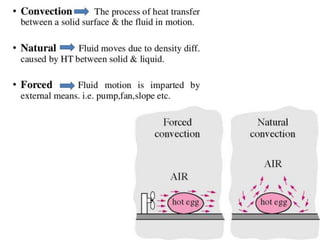
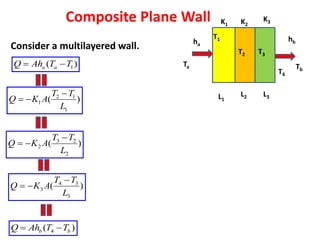
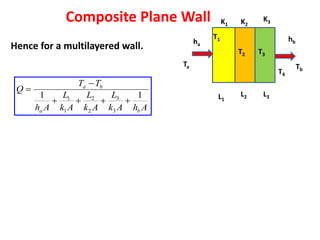
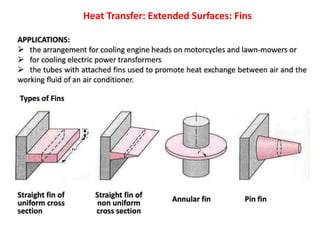
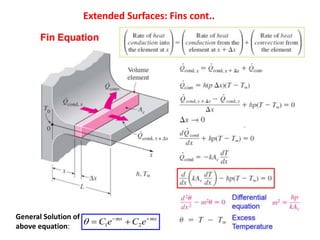
Heat transfer analysis is needed to optimally design heat exchangers and determine equipment sizes. It is essential for sizing nuclear reactor cores, aircraft performance, refrigeration applications, and solar equipment. Thermodynamic analysis determines the heat required for a state change, while heat transfer analysis evaluates the rate of heat transfer. The three methods of heat transfer are conduction through solids, convection through fluid movement, and radiation through electromagnetic waves. Extended surfaces like fins increase heat transfer area and rates.

1. HEAT TRANSFER
VED PRAKASH
Email id- vedprakash.sp@gmail.com
Mob-8698719509

2. Why do we need Heat transfer Analysis?
The optimal design of heat exchangers such as
boilers, heaters, refrigerators and radiators is a
detailed analysis of heat transfer.
This is essential to determine the feasibility and
cost of the undertaking, as well as the size of
equipment required to transfer a specified
amount of heat transfer in a given time.
Proper sizing of fuel elements in the nuclear
reactor cores to prevent burnout.

3. Performance of Aircraft
An accurate heat transfer analysis is necessary in
the refrigeration and air-conditioning
applications to calculate the heat loads, and to
determine the thickness of insulation to avoid
excess in heat gains or losses
Solar collectors and associated equipment

4. Heat
How much heat is required to bring a system
from one equilibrium state to another is the
main criteria in Thermodynamic analysis
In heat transfer analysis we evaluate how fast
the change of state occurs by calculating the
rate of heat transfer in joule/sec or watt
Thermodynamic analysis
( Q in joules)
Heat transfer Analysis
( Q in watt)

5. Heat Transfer Methods
• Heat transfers in three ways:
–Conduction
–Convection
–Radiation

6. Conduction
 Conduction is the transfer of heat through a solid or
from one solid to another
 When you heat a metal strip at one end, the heat travels
to the other end
As you heat the metal, the particles vibrate, these vibrations make
the adjacent particles vibrate, and so on and so on, the vibrations
are passed along the metal and so is the heat. This IS KNOWN AS
Conduction

13. Q1- A stainless steel plate 2 cm thick is maintained at
a temperature of 550°C at one face and 50°C on the
other. The thermal conductivity of stainless steel at
300°C is 19.1 W/mK. Compute the heat transferred
through the material per unit area.

14. 𝑄𝑥 =
𝐾𝐴
𝐿
(T1-T2)
𝑄𝑥
𝐴
=
𝐾
𝐿
(T1-T2) =
(19.1)
0.02
(550-50) = 477.5 kW/m2

15. Q2-

18. L1
L2 L3
K1 K2
K3
Ta Tb
ha
hb
T1
T4
T2 T3
Composite Plane Wall
Consider a multilayered wall.
1
( )
a a
Q Ah T T
 
2 1
1
1
( )
T T
Q K A
L

 
3 2
2
2
( )
T T
Q K A
L

 
4 3
3
3
( )
T T
Q K A
L

 
4
( )
b b
Q Ah T T
 

19. L1
L2 L3
K1 K2
K3
Ta Tb
ha
hb
T1
T4
T2 T3
Composite Plane Wall
Hence for a multilayered wall.
3
1 2
1 2 3
1 1
a b
a b
T T
Q
L
L L
h A k A k A k A h A


   

20. 1.

23. Heat Transfer: Extended Surfaces: Fins

24. Extended Surfaces: Fins cont..
General Solution of
above equation: 1 2
mx mx
C e C e
  
 

25. Extended Surfaces: Fins cont..
Case 1: Long Fins:
0
mx
T T
e
T T





  
0
Q hPkA T T
 
Case 2: Fins with insulated end:
 
 
0
cosh
cosh
m L x
T T
T T mL


 

  


   
0 tanh
Q hPkA T T mL

 
Case 3: Fins with Convection off the end: ( Uninsulated end)
Put L= Lc in Case2
Where, Lc = Corrected length
= L+ t/2 for Rectangular fin
= L+ d/4 for pin fin

26. Q1: A Rectangular fin of length 30cm, width 30cm and
thickness 2mm is attached to a surface at 300°C. The fin is
made of aluminium ( K= 204 w/mK ) and is exposed to air at
30°C . The fin end is uninsulated and can lose heat through its
end also. The convection heat transfer coefficient between
the fin surface and air is 15 w/m2K. Determine:
1- The rate of heat transfer from the fin
2- The temperature of the fin at 30cm from the base

27. Q2: A fin has 5mm dia and 100mm long. The
conductivity(K) of fin material is 400 w/mK. One end of the
fin is maintained at 130°C and its remaining surface is
exposed to ambient air at 30°C. If the convective heat
transfer coefficient is 40 w/m2K, the heat loss is watts from
the fin is?
Hint- Case2

28. Q3: An electronic semiconductor device generate heat equal
to 0.48 watt in order to keep the surface temperature at the
upper safe limit of 70°C, the generated heat has to be
dissipated to the surrounding which is at 30°C. To accomplish
this task, aluminium fins of 0.7mm square and 12mm long
are attached to the surface. The thermal conductivity of fin
material is 170 w/mK. If the heat transfer coefficient is 12
w/m2K, calculate the number of fins required . Assume no
heat loss from the tip of fins.

29. The third method of heat transfer
How does heat energy get from the
Sun to the Earth?
There are no particles between
the Sun and the Earth so it
CANNOT travel by conduction
or by convection.
?
RADIATION

31. Thank You