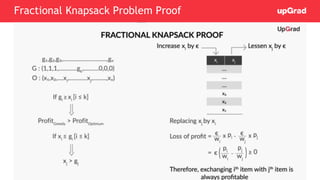
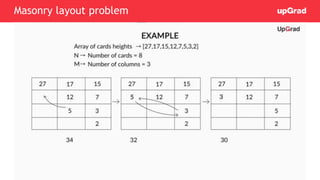
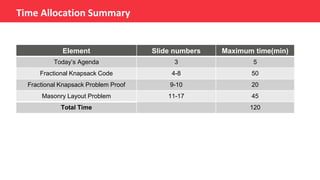
This document summarizes topics to be covered in a class on greedy algorithms, including the fractional knapsack problem, fractional knapsack problem proof, and masonry layout problem. It provides code for the fractional knapsack problem that implements a greedy approach of sorting items by value/weight ratio and filling the knapsack accordingly. It also discusses using a greedy approach for the masonry layout problem by keeping column lengths close to the average card size.

1. EditEdit
MasterMaster
texttext stylesstyles
Module Name - Greedy
Algorithms
Class - Day 3
Topic Name: Fractional
Knapsack Implementation,
Masonry Layout

2. Time Allocation Summary
Element Slide numbers Maximum time(min)
Today’s Agenda 3 5
Fractional Knapsack Code 4-8 50
Fractional Knapsack Problem Proof 9-10 20
Masonry Layout Problem 11-17 45
Total Time 120

3. ● Fractional Knapsack Problem
● Fractional Knapsack Problem Proof
● Masonry Layout Problem
Today’s Agenda

4. ● As expected, the greedy approach for fractional knapsack does not apply to
0-1 knapsack.
● Now that we know the working behind the fractional knapsack greedy
approach, let us write the code for it:
● Given weights and values of n items, we need to put these items in a
knapsack of capacity W to get the maximum total value in the knapsack.
● In the 0-1 Knapsack problem, we are not allowed to break items. We either
take the whole item or don’t take it.
Fractional Knapsack Problem

5. Input:
Items as (value, weight) pairs
arr[] = {{60, 10}, {100, 20}, {120, 30}}
Knapsack Capacity, W = 50;
Output:
Maximum possible value = 240
by taking items of weight 10 and 20 kg and 2/3 fraction
of 30 kg. Hence total price will be 60+100+(2/3)(120) = 240
● Calculate the ratio value/weight for each item and sort the item on basis of
this ratio.
● Take the item with the highest ratio and add them until we can’t add the next
item as a whole and at the end add the next item as much as we can which
will always be the optimal solution to this problem.
Fractional Knapsack Problem

6. public class FractionalKnapSack {
private static double getMaxValue(int[] wt, int[] val, int capacity)
{
ItemValue[] iVal = new ItemValue[wt.length];
for (int i = 0; i < wt.length; i++) {
iVal[i] = new ItemValue(wt[i], val[i], i);
}
Arrays.sort(iVal, new Comparator<ItemValue>() {
public int compare(ItemValue o1, ItemValue o2)
{
return o2.cost.compareTo(o1.cost);
}
});
double totalValue = 0d;
Fractional Knapsack Problem

7. for (ItemValue i : iVal) {
int curWt = (int)i.wt;
int curVal = (int)i.val;
if (capacity - curWt >= 0) {
capacity = capacity - curWt;
totalValue += curVal;
}
else {
double fraction = ((double)capacity / (double)curWt);
totalValue += (curVal * fraction);
capacity = (int) (capacity - (curWt * fraction));
break;
}
}
return totalValue;
}
Fractional Knapsack Problem

8. static class ItemValue { // item value class
Double cost;
double wt, val, ind;
public ItemValue(int wt, int val, int ind) {
this.wt = wt;
this.val = val;
this.ind = ind;
cost = new Double((double)val / (double)wt);
}
}
public static void main(String[] args){
int[] wt = { 10, 40, 20, 30 };
int[] val = { 60, 40, 100, 120 };
int capacity = 50;
double maxValue = getMaxValue(wt, val, capacity);
System.out.println("Maximum value we can obtain = " + maxValue);
}
}
Fractional Knapsack Problem

9. Let’s see if we can prove the correctness of our greedy approach.
Fractional Knapsack Problem Proof

10. Fractional Knapsack Problem Proof

11. We learnt that greedy algorithms can be used to solve a number of
problems optimally.
But greedy algorithms can be quite useful even for problems that they
can’t solve optimally.
In fact they give solutions close to optimal solution without much
complexity.
Let us understand this importance through an industrial problem called
masonry layout.
Masonry layout problem

12. Masonry layout problem

13. Websites like Pinterest try to increase the time users spend on their
pages by maximizing the images shown on screen.
Masonry layout problem

14. Masonry layout problem

15. What should be our greedy approach to solve this problem?
Here we would take average of card size from all the cards and try to
keep the length of each column to average.
We already talked that greedy approach might not give optimal results but
the solution can be close to optimal one.
Let us write the code for the same.
Masonry layout problem

16. Masonry layout problem

17. Here even though we know that our approach provides sub optimal
solution we still prefer the greedy approach.
This is because the approach for optimal solution is very complex and
takes much more time for the calculations.
Greedy algorithms on the other hand are easy to implement, fast and
provide close to optimal solutions.
Masonry layout problem

18. Thank You!
#LifeKoKaroLift