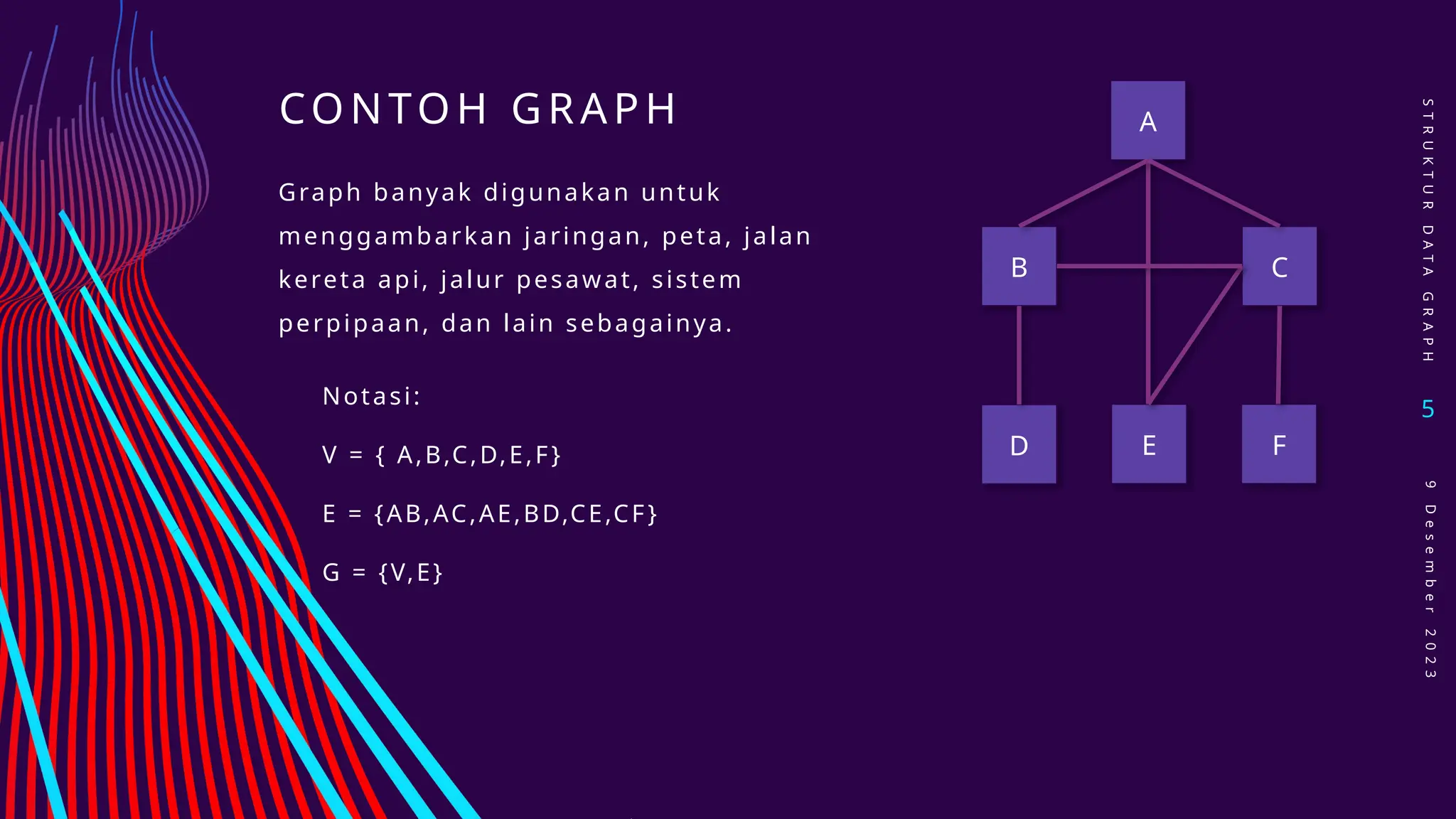
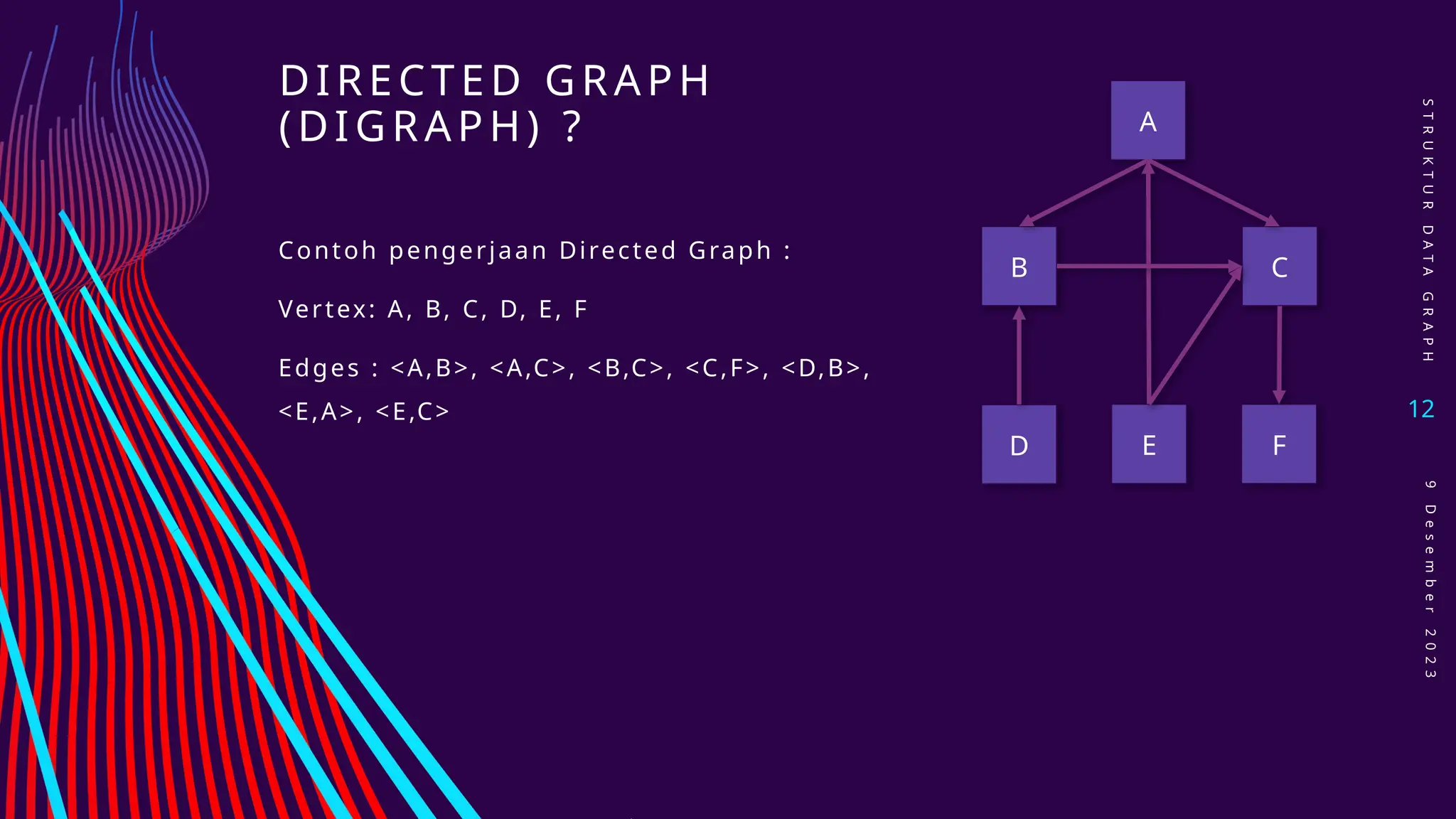
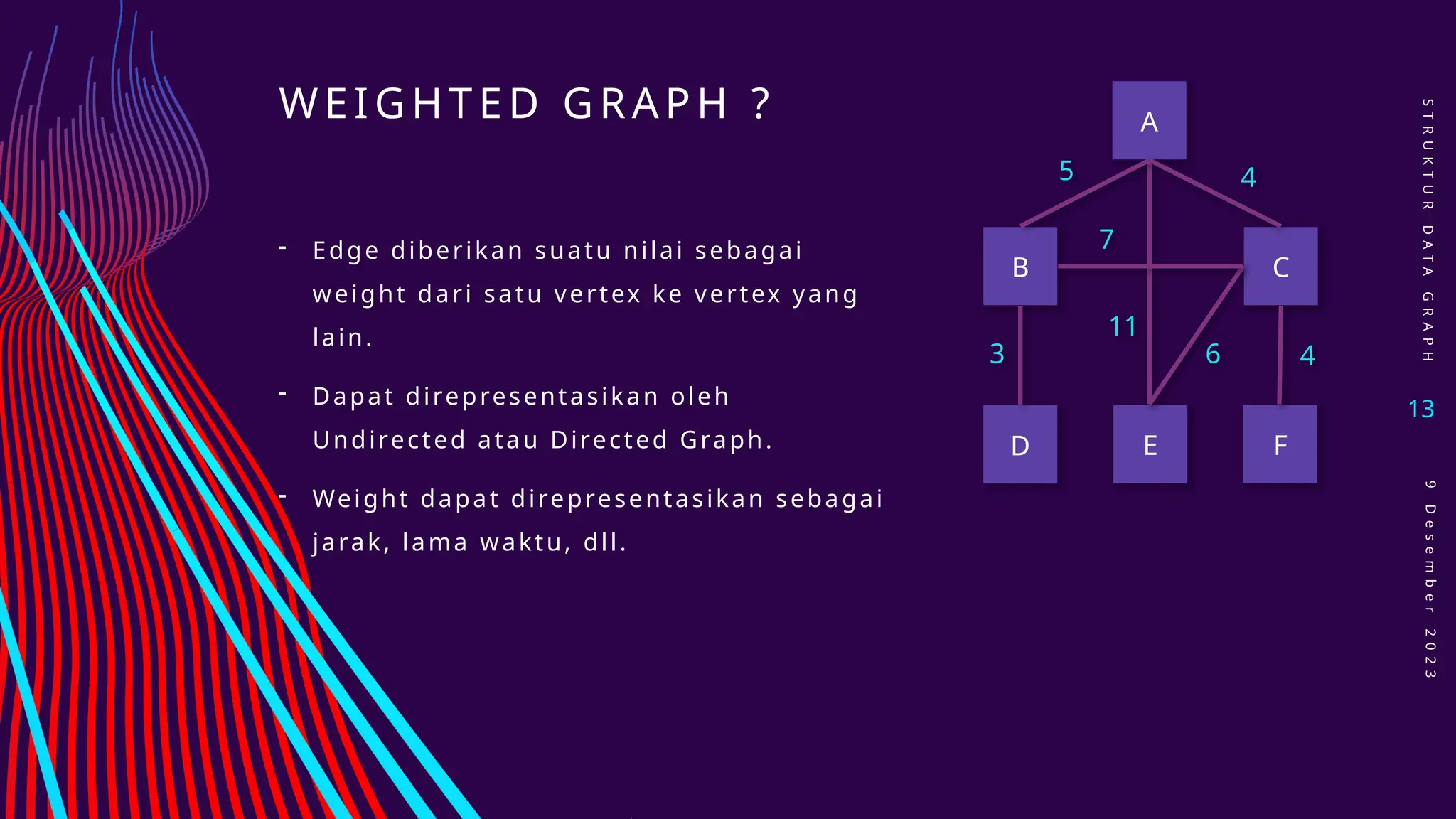
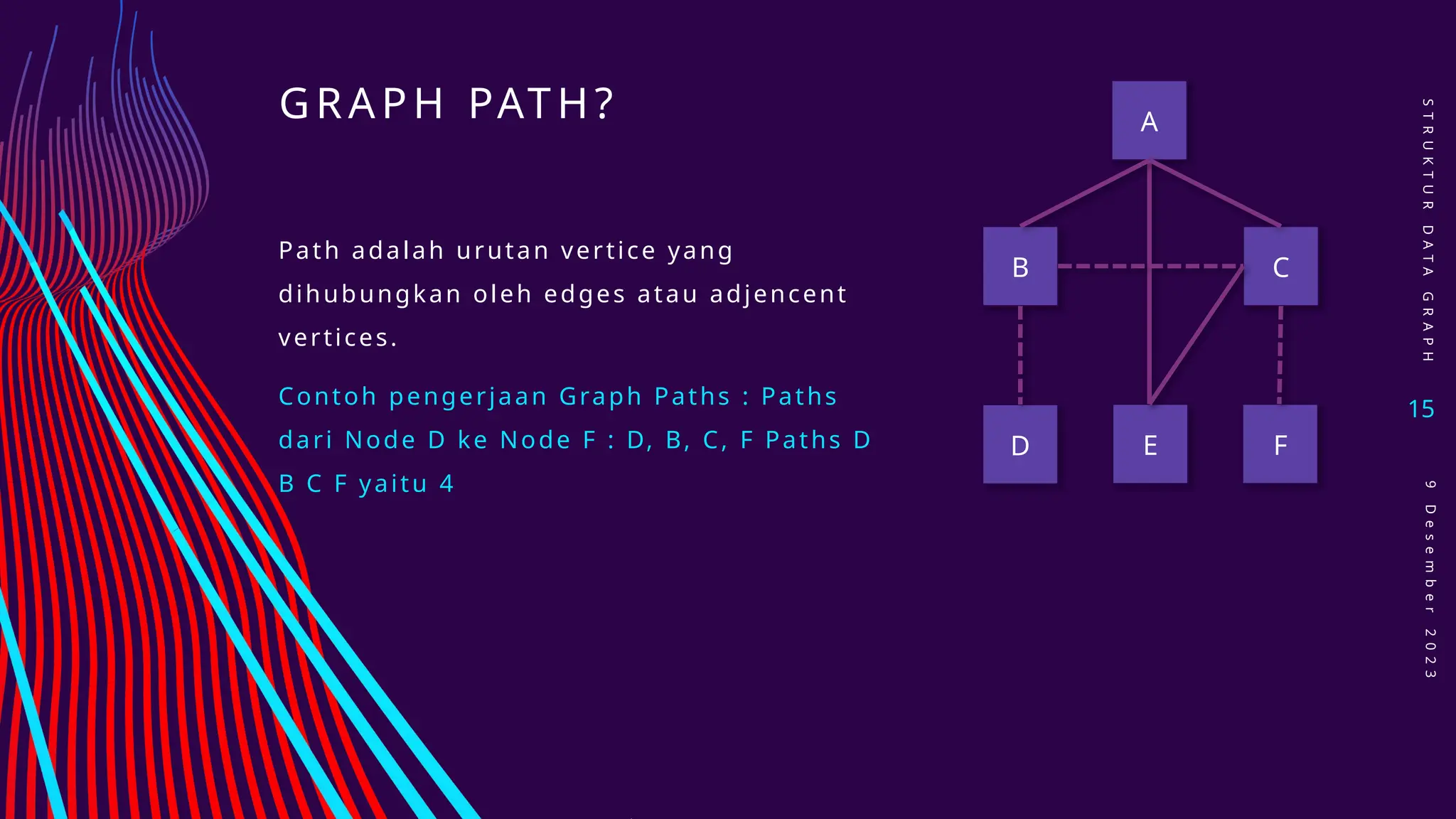
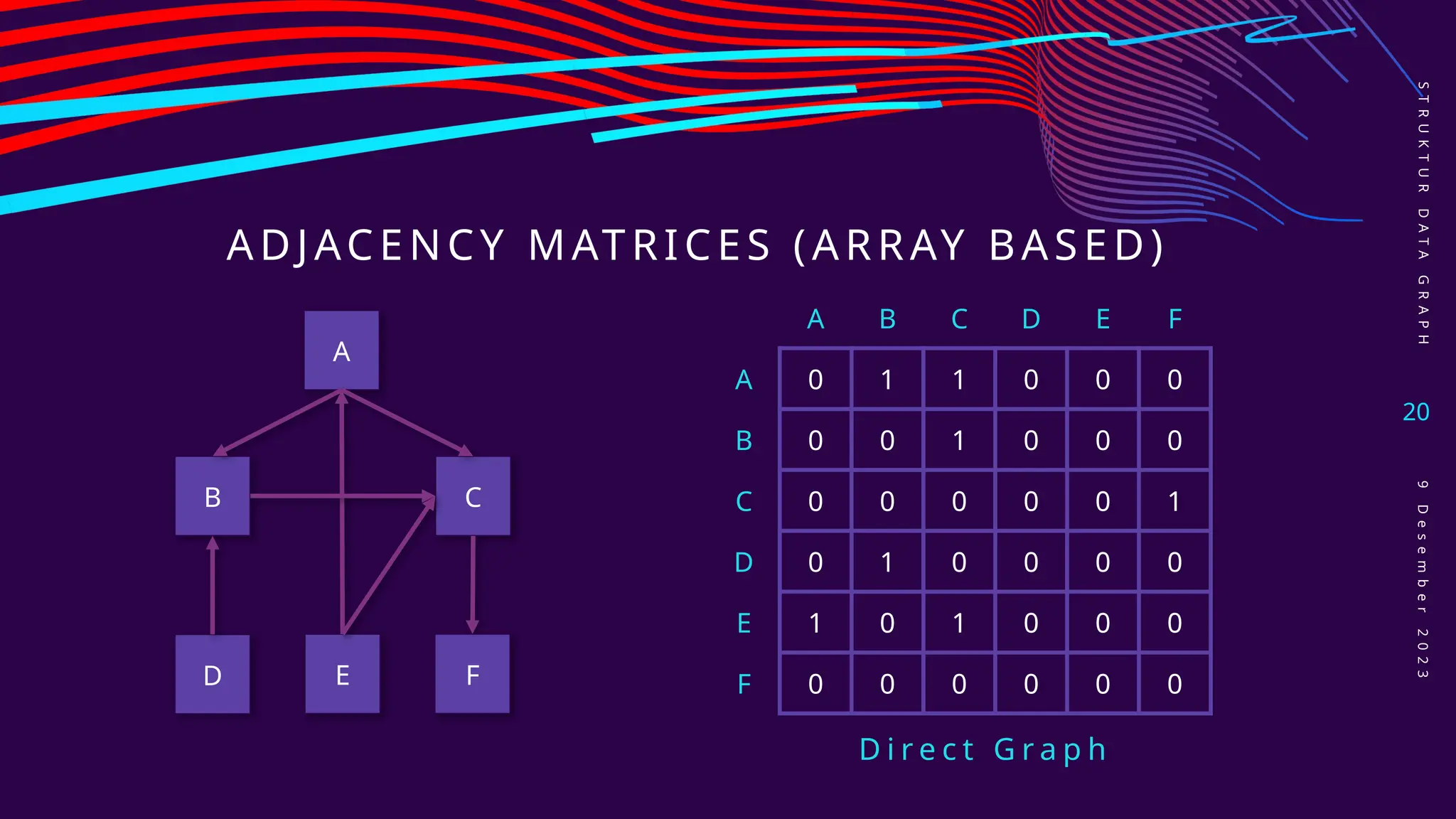
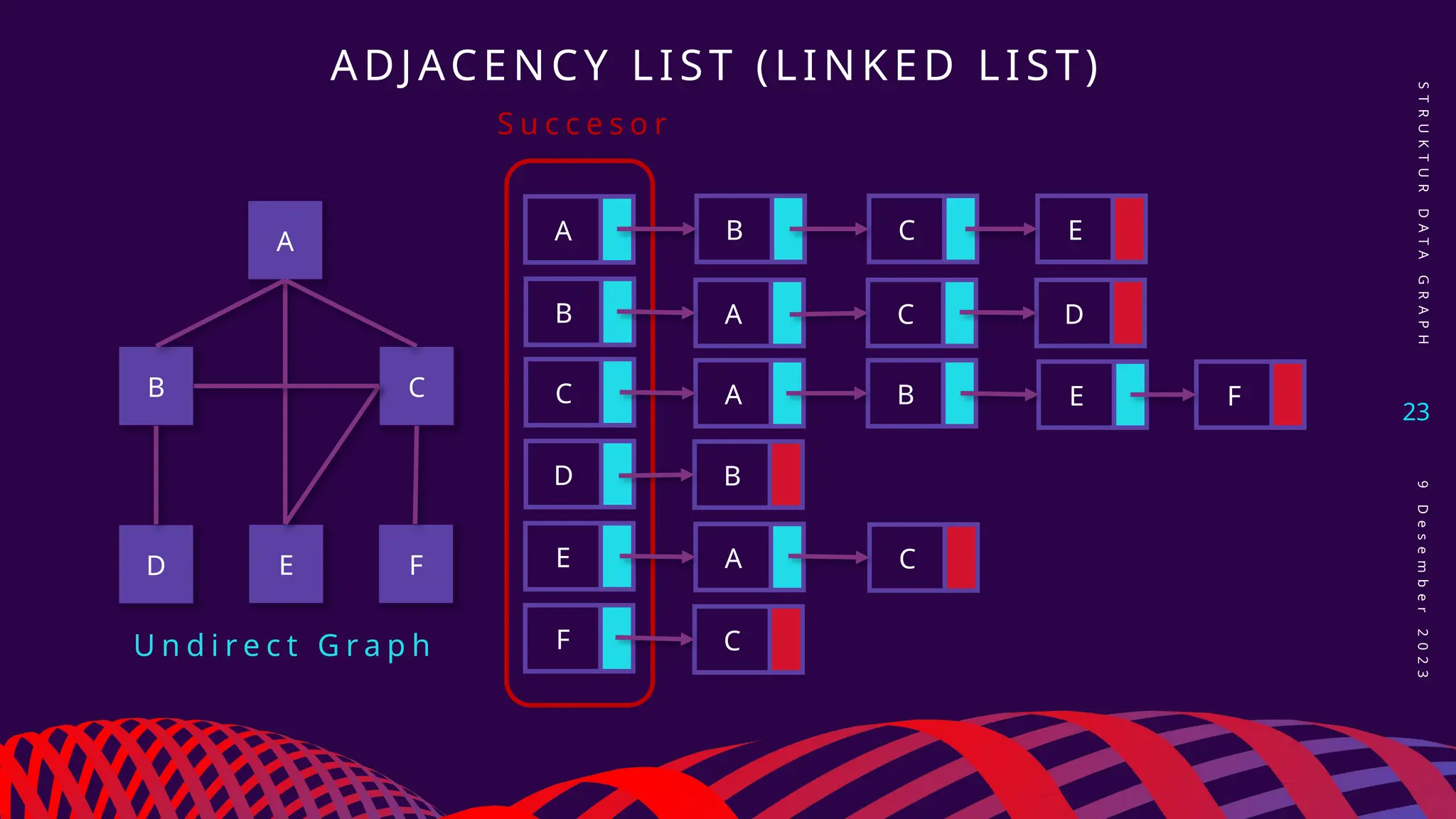
Dokumen ini membahas struktur data graph, termasuk konsep dasar, jenis-jenis graph seperti undirected, directed, dan weighted graph, serta berbagai metode implementasi seperti adjacency matrices dan adjacency lists. Selain itu, dijelaskan juga masalah-masalah yang berkaitan dengan graph, seperti shortest path problem dan minimum spanning tree problem. Terdapat juga penjelasan mengenai operasi yang dapat dilakukan pada graph, seperti menambah atau menghapus vertex dan edge.

1. GRAPH
STRUKTUR
DATA
Sabtu, 9 Desember 2023

2. KELOMPOK 6
Abdul Majid Tanjung
Aldin Noverman Telaumbanua
Iperusman Zai
Michael Laowo
Santi Trimurni Buulolo

3. YANG DI PELA JARI?
- Konsep Graph
- Masalah yang dihadapi Graph
- Jenis-Jenis Graph
- Struktur data Linear, Tree, Graph
- Operasi Graph
- Konsep Implementasi Graph
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
3
9
D
e
s
e
m
b
e
r
2
0
2
3

4. KONSEP GRAPH
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
4
9
D
e
s
e
m
b
e
r
2
0
2
3
- Konsep struktur data yang terdiri dari
Node(Vertex atau Vertices) dan Garis
penghubung(Arc atau Edge)
- Keterhubungan Graph dapat membentuk
relasi One-to-One, One-to-Many, Many-
to-One, dan Many-to-Many.
A
B C
F
E
D

5. CONTOH GRAPH
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
5
9
D
e
s
e
m
b
e
r
2
0
2
3
Graph banyak digunakan untuk
menggambarkan jaringan, peta, jalan
kereta api, jalur pesawat, sistem
perpipaan, dan lain sebagainya.
A
B C
F
E
D
Notasi:
V = { A,B,C,D,E,F}
E = {AB,AC,AE,BD,CE,CF}
G = {V,E}

6. MASALAH-MASALAH GRAPH
- Sho rtest P ath Problem (Masalah Patch
Minimum)
- Ma ximum Flow
Pro blem(Ma sala hAliranMaksimum)
- Gra ph Searching Problem (Ma salah
Penca ria n dalam Gra ph)
- To po logical Ordering P roblem (Ma sa lah
Pengurutan Topo logi)
- Task Network Pro blem (Masalah Jaringan
Tugas)
- Minimum Spanning Tree Pro blem (Ma sala h
Penca ria n Pohon RentangMinimum)
- Tra velling Sa lesperso n P roblem
- Four-color P roblem

7. S T R U K T U R DATA L I N E A R V S T R E E V S G R A P H
S
T
U
R
K
T
U
R
D
A
T
A
G
R
A
P
H
7
9
D
e
s
e
m
b
e
r
2
0
2
3
- Struktur Data Linear : Menyimpan elemen data secara berurutan, sehingga
setiap elemen memiliki posisi yang tetap dan unik.
- Struktur Data Tree : Menyimpan elemen data secara hierarkis, sehingga
setiap elemen memiliki hubungan induk-anak dengan elemen lain.
- Struktur Data Graph : Menyimpan elemen data secara tidak terbatas,
sehingga setiap elemen dapat memiliki hubungan apa pun dengan elemen
lain.

8. KATEGORI GRAPH
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
8
9
D
e
s
e
m
b
e
r
2
0
2
3
- Undirected Graph
- Directed Graph
- Weighted Graph
A
B C
F
E
D

9. UNDIRECTED GRAPH
(UNDIGRAPH) ?
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
9
9
D
e
s
e
m
b
e
r
2
0
2
3
- Edge tidak ada penugasan arah dari
satu vertex ke vertex yang lain.
- Digunakan untuk mempresentasikan
relasi One-to-One.
- Jika A dan B adalah vertex, maka edge
dapat mempresentasikan sebagai (A,B)
dan (B,A).
A
B C
F
E
D

10. UNDIRECTED GRAPH
(UNDIGRAPH) ?
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
10
9
D
e
s
e
m
b
e
r
2
0
2
3
Contoh pengerjaan Undirected Graph :
V : A, B, C, D, E, F
E : (A,B), (A,C), (A,E), (B,A), (B,C), (B,D),
(C,A), (C,B), (C,E), (C,F), (D,B), (E,A), (E,C),
(F,C)
A
B C
F
E
D

11. DIRECTED GRAPH
(DIGRAPH) ?
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
11
9
D
e
s
e
m
b
e
r
2
0
2
3
- Edge ada penugasan arah dari satu
vertex ke vertex yang lain.
- Edges antar Vertexs diwakilkan dengan
kurung sudut.
- Jika vertex A sebagai sumber dan
menunju ke vertex B sebagai tujuan,
maka edge dapat mempresentasikan
sebagai <A,B>
A
B C
F
E
D

12. DIRECTED GRAPH
(DIGRAPH) ?
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
12
9
D
e
s
e
m
b
e
r
2
0
2
3
Contoh pengerjaan Directed Graph :
Vertex: A, B, C, D, E, F
Edges : <A,B>, <A,C>, <B,C>, <C,F>, <D,B>,
<E,A>, <E,C>
A
B C
F
E
D

13. WEIGHTED GRAPH ?
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
13
9
D
e
s
e
m
b
e
r
2
0
2
3
- Edge diberikan suatu nilai sebagai
weight dari satu vertex ke vertex yang
lain.
- Dapat direpresentasikan oleh
Undirected atau Directed Graph.
- Weight dapat direpresentasikan sebagai
jarak, lama waktu, dll.
5 4
7
3
11
6 4
A
B C
F
E
D

14. WEIGHTED GRAPH ?
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
14
9
D
e
s
e
m
b
e
r
2
0
2
3
Contoh pengerjaan Undirected Weight
Graph :
Vertex: A, B, C, D, E, F
Edges : (A,B) = 5, (A,C) = 4, (A,E) = 11, (B,A)
= 5, (B,C) = 7, (B,D) = 3, (C,A) = 4, (C,B) = 7,
(C,E) = 6, (C,F) = 4, (D,B) = 3, (E,A) = 11,
(E,C) = 6, (F,C) = 4
5 4
7
3
11
6 4
A
B C
F
E
D

15. GRAPH PATH?
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
15
9
D
e
s
e
m
b
e
r
2
0
2
3
Path adalah urutan vertice yang
dihubungkan oleh edges atau adjencent
vertices.
Contoh pengerjaan Graph Paths : Paths
dari Node D ke Node F : D, B, C, F Paths D
B C F yaitu 4
A
B C
F
E
D

16. OPERASI PADA
GRAPH?
- Add Vertex : menambahvertex baruke dalamgraph.
- Delete Vertex : menghapus vertex tertentu disuatu graph.
- Add Edge : menambahedge baruyang menghubungkan
antarvertex disuatu graph.
- Delete Edge : menghapus suatu edge yang menghubungkan
antar vertex disuatu graph.
- Search Path : mencaripanjang paths darisuatu vertex ke
vertex yang lain.
- Tranversing : penelusuran dari vertex ke vertex lainnya
dengan penghubung edge

17. KONSEP IMPLEMENTASI GRAPH
17
- Adjacency Matrices (Array Based) :
implementasi menggunakan array
matriks.
- Adjecency List (Linked List) :
implementsi menggunakan linked list
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
9
D
e
s
e
m
b
e
r
2
0
2
3

18. ADJACENCY MATRICES (ARRAY
BASED)
18
- Representasinya dengan array 2 dimensi
atau matriks.
- Pada Undirect & Direct Graph 0 berarti
tidak ada relasi edge, sedangkan nilai 1
ada relasi edge.
- Pada Weighted Graph nilainya diisi nilai
beban edge nya
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
9
D
e
s
e
m
b
e
r
2
0
2
3

19. ADJACENCY MATRICES (ARRAY BASED)
19
A B C D E F
A 0 1 1 0 1 0
B 1 0 1 1 0 0
C 1 1 0 0 1 1
D 0 1 0 0 0 0
E 1 0 1 0 0 0
F 0 0 1 0 0 0
U n d i r e c t G r a p h
A
B C
F
E
D
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
9
D
e
s
e
m
b
e
r
2
0
2
3

20. ADJACENCY MATRICES (ARRAY BASED)
20
A B C D E F
A 0 1 1 0 0 0
B 0 0 1 0 0 0
C 0 0 0 0 0 1
D 0 1 0 0 0 0
E 1 0 1 0 0 0
F 0 0 0 0 0 0
D i r e c t G r a p h
A
B C
F
E
D
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
9
D
e
s
e
m
b
e
r
2
0
2
3

21. ADJACENCY MATRICES (ARRAY BASED)
21
A B C D E F
A 0 5 4 0 11 0
B 5 0 7 3 0 0
C 4 7 0 0 6 4
D 0 3 0 0 0 0
E 11 0 6 0 0 0
F 0 0 4 0 0 0
U n d i r e c t W i g h t e d G r a p h
5 4
7
3
11
6 4
A
B C
F
E
D
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
9
D
e
s
e
m
b
e
r
2
0
2
3

22. ADJACENCY LIST (LINKED LIST)
22
- epresentasinya dengan linked list.
- Node asal akan disebut Successor.
- Isi dari successor akan diisi list node
yang berkaitan, node terakhir akan diisi
pada nextnya.
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
9
D
e
s
e
m
b
e
r
2
0
2
3

23. 23
ADJACENCY LIST (LINKED LIST)
U n d i r e c t G r a p h
A
B C
F
E
D
A
B
C
D
E
F
B C E
A C D
A B F
A C
C
E
B
S u c c e s o r
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
9
D
e
s
e
m
b
e
r
2
0
2
3

24. 24
ADJACENCY LIST (LINKED LIST)
D i r e c t G r a p h
A
B
C
D
E
F
B C
D
F
A C
B
S u c c e s o r
A
B C
F
E
D
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
9
D
e
s
e
m
b
e
r
2
0
2
3

25. 25
ADJACENCY LIST (LINKED LIST)
U n d i r e c t W i g h t e d G r a p h
A
B
C
D
E
F
B(5) C(4) E(11)
A(5) C(7) D(3)
A(4) B(7) F(4)
A(11
)
C(6)
C(4)
E(6)
B(3)
S u c c e s o r
5 4
7
3
11
6 4
A
B C
F
E
D
S
T
R
U
K
T
U
R
D
A
T
A
G
R
A
P
H
9
D
e
s
e
m
b
e
r
2
0
2
3

26. THANK YOU