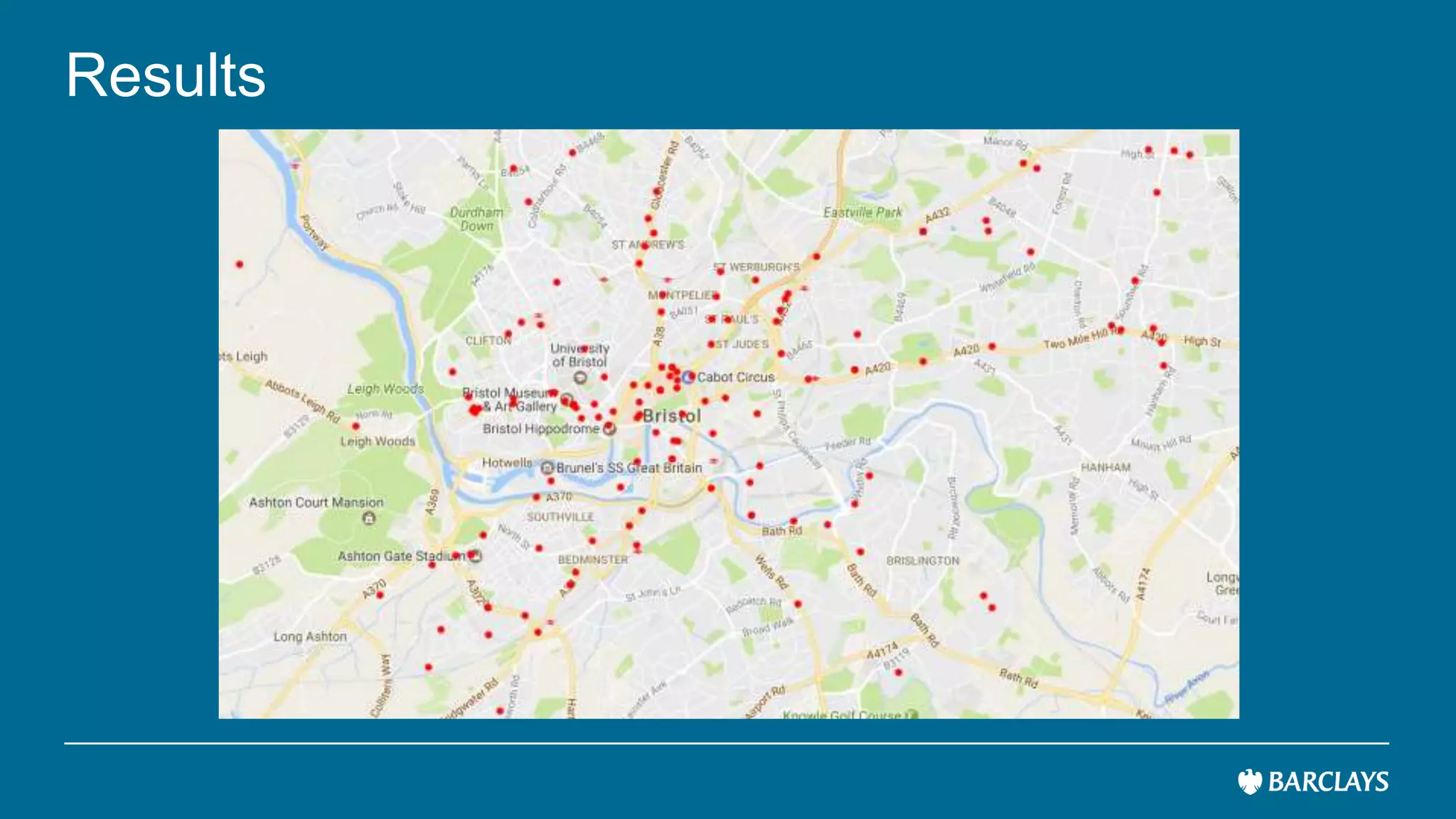
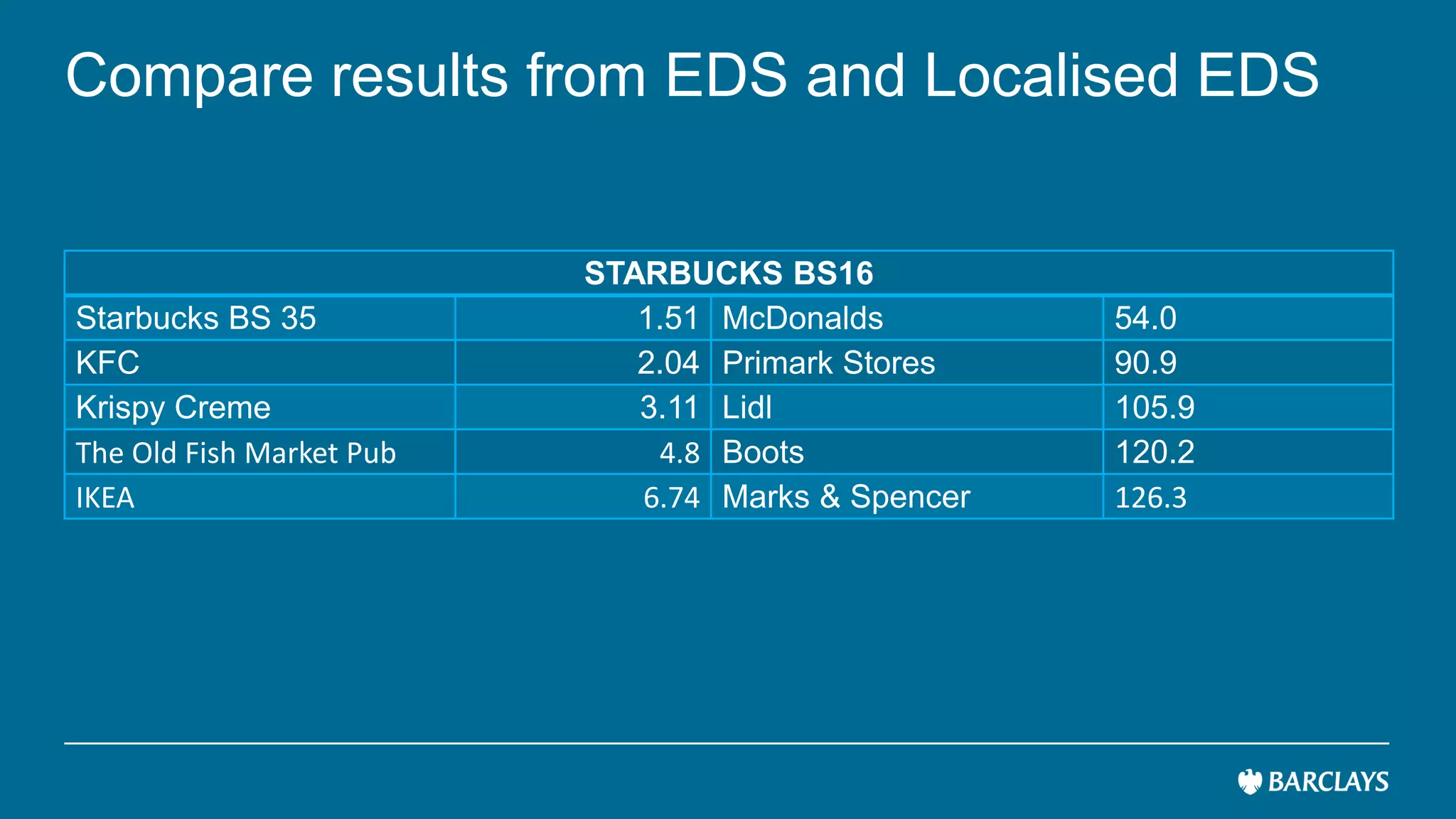
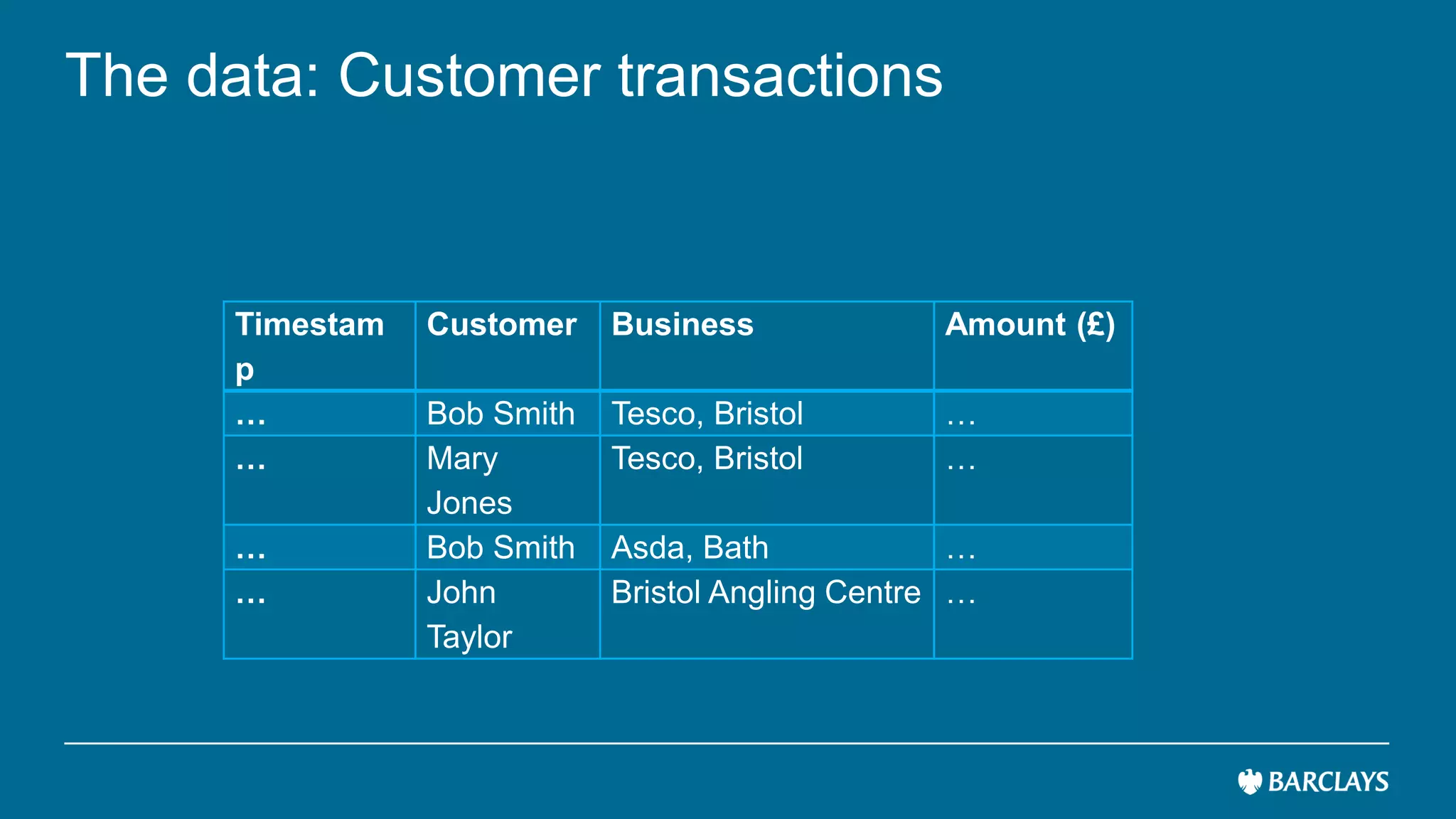
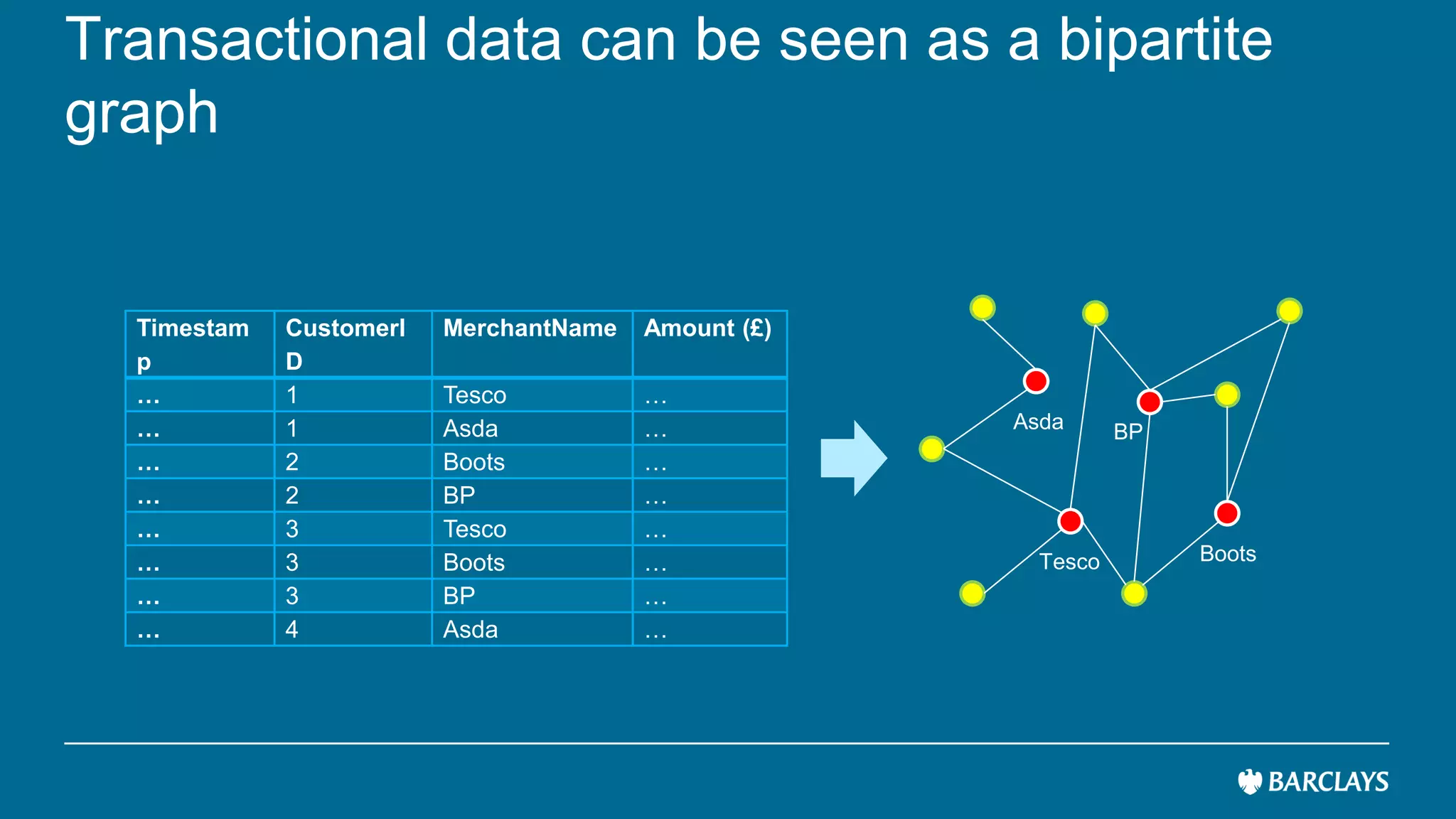
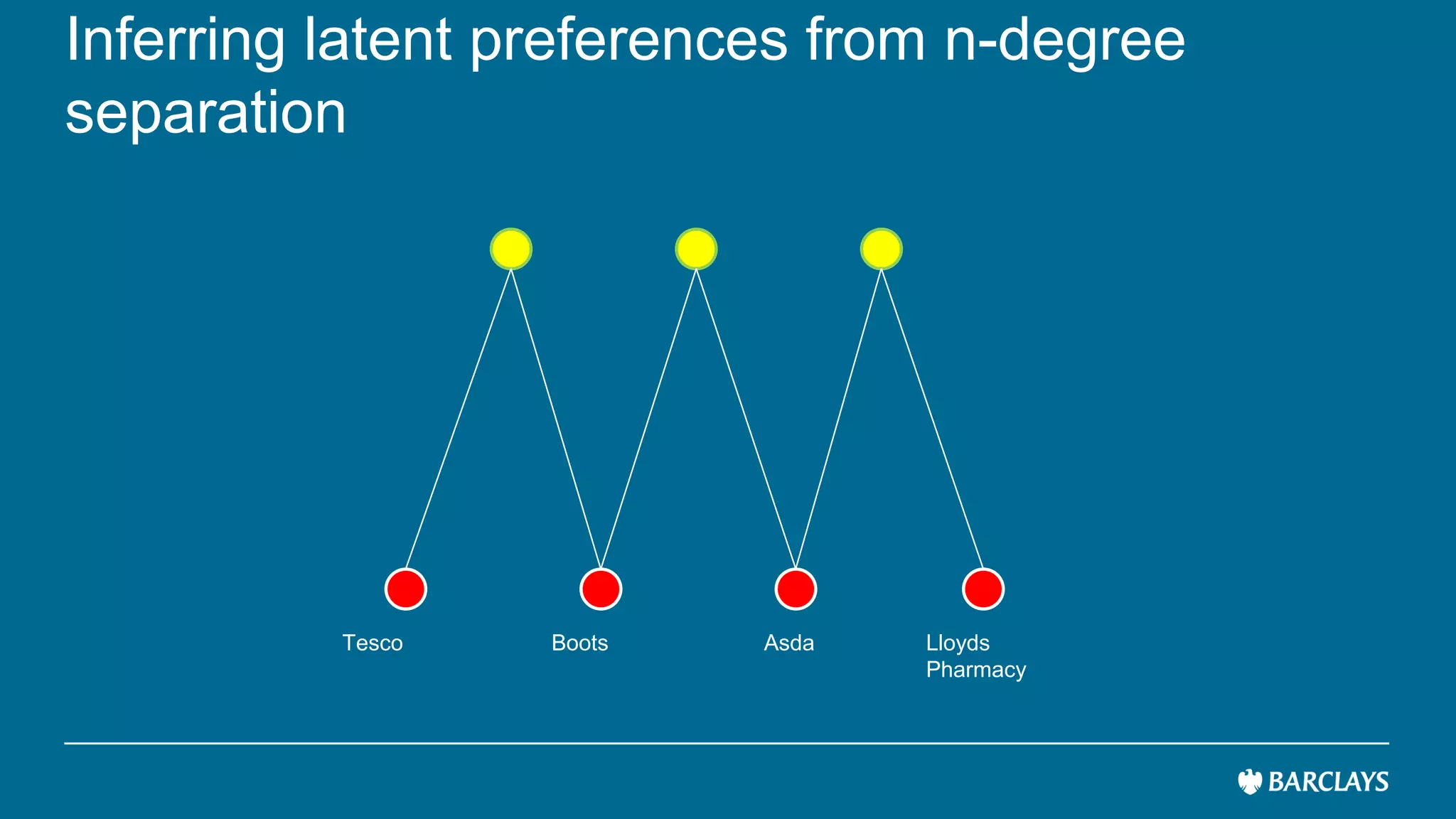
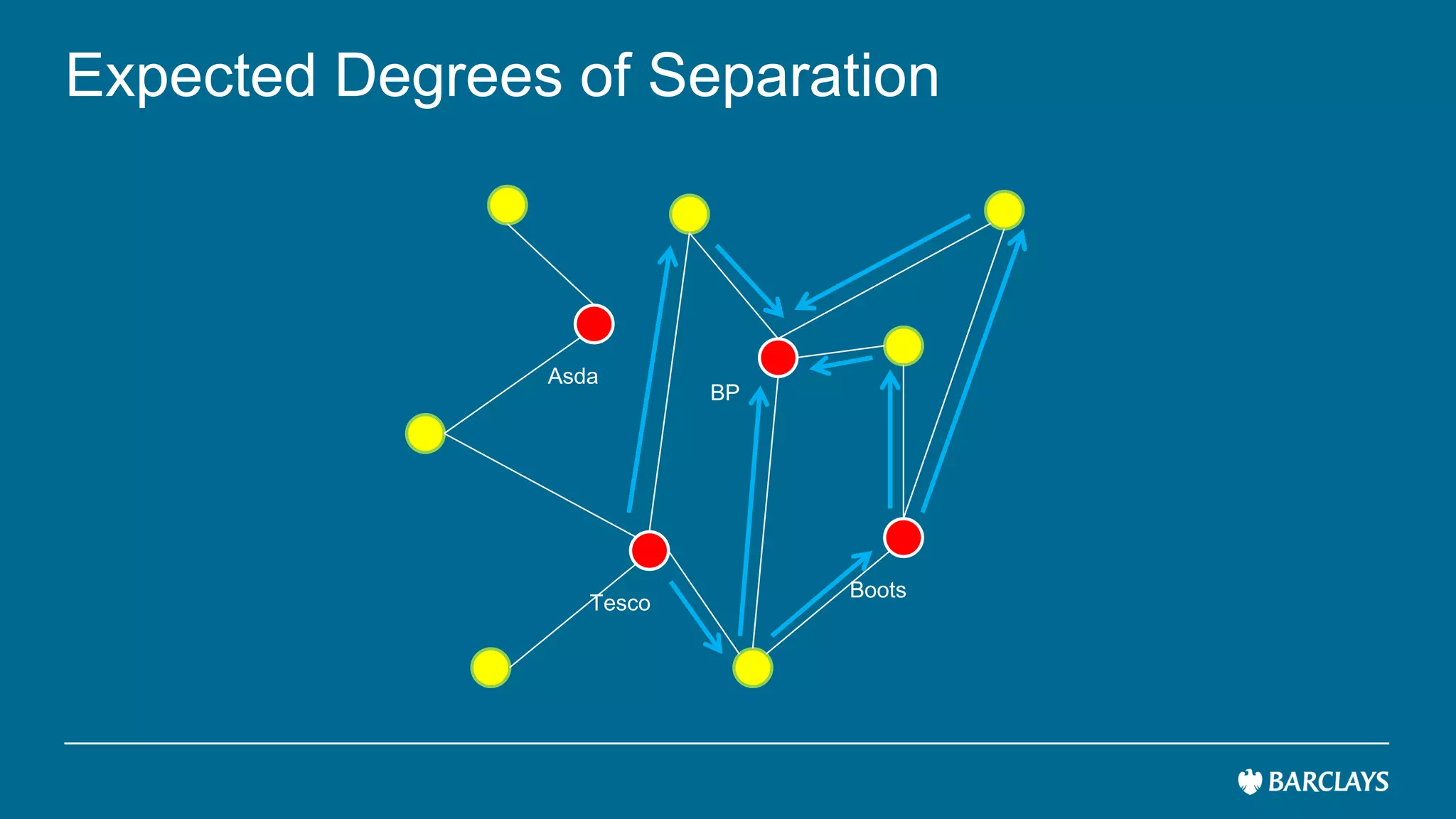
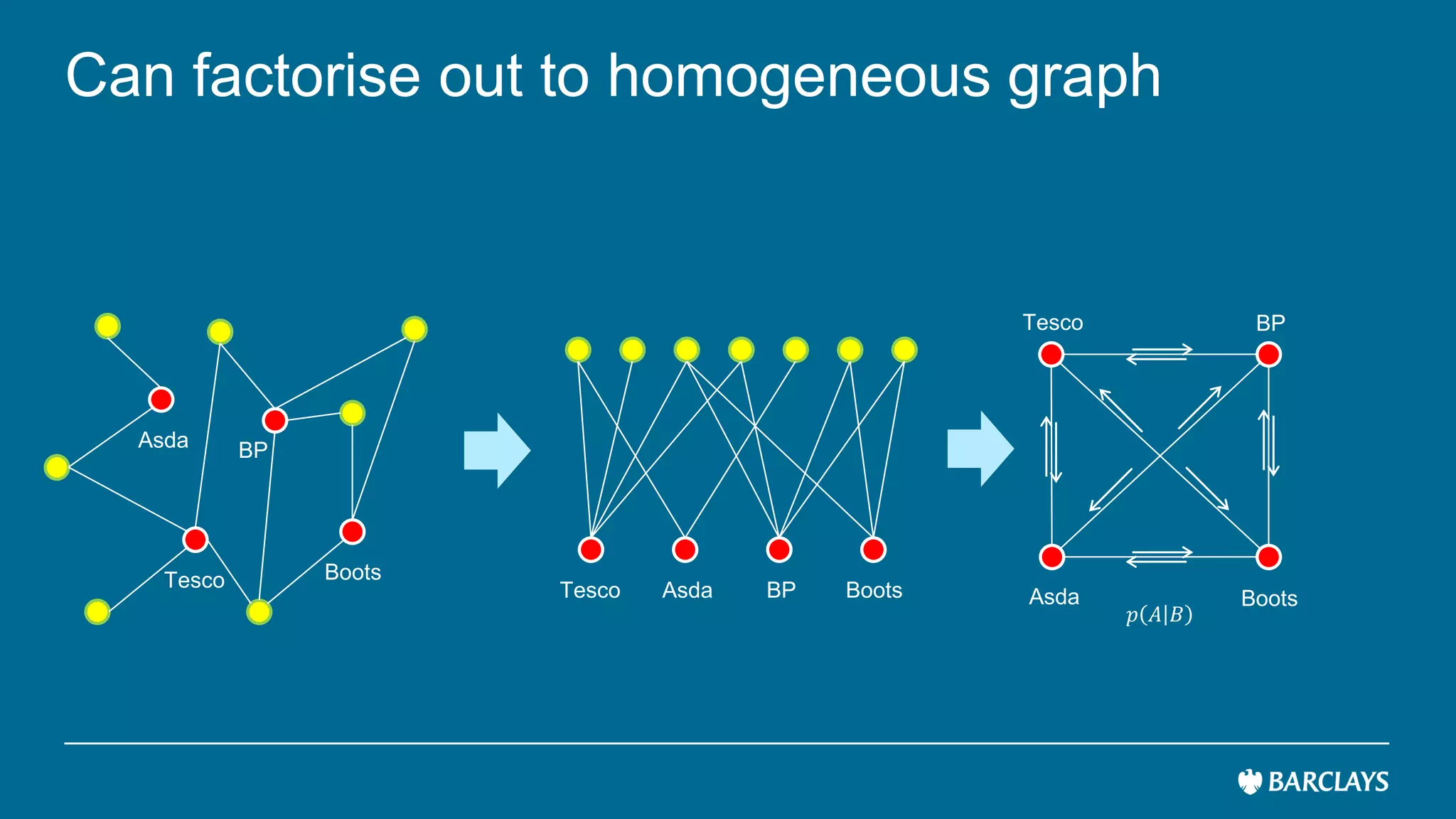
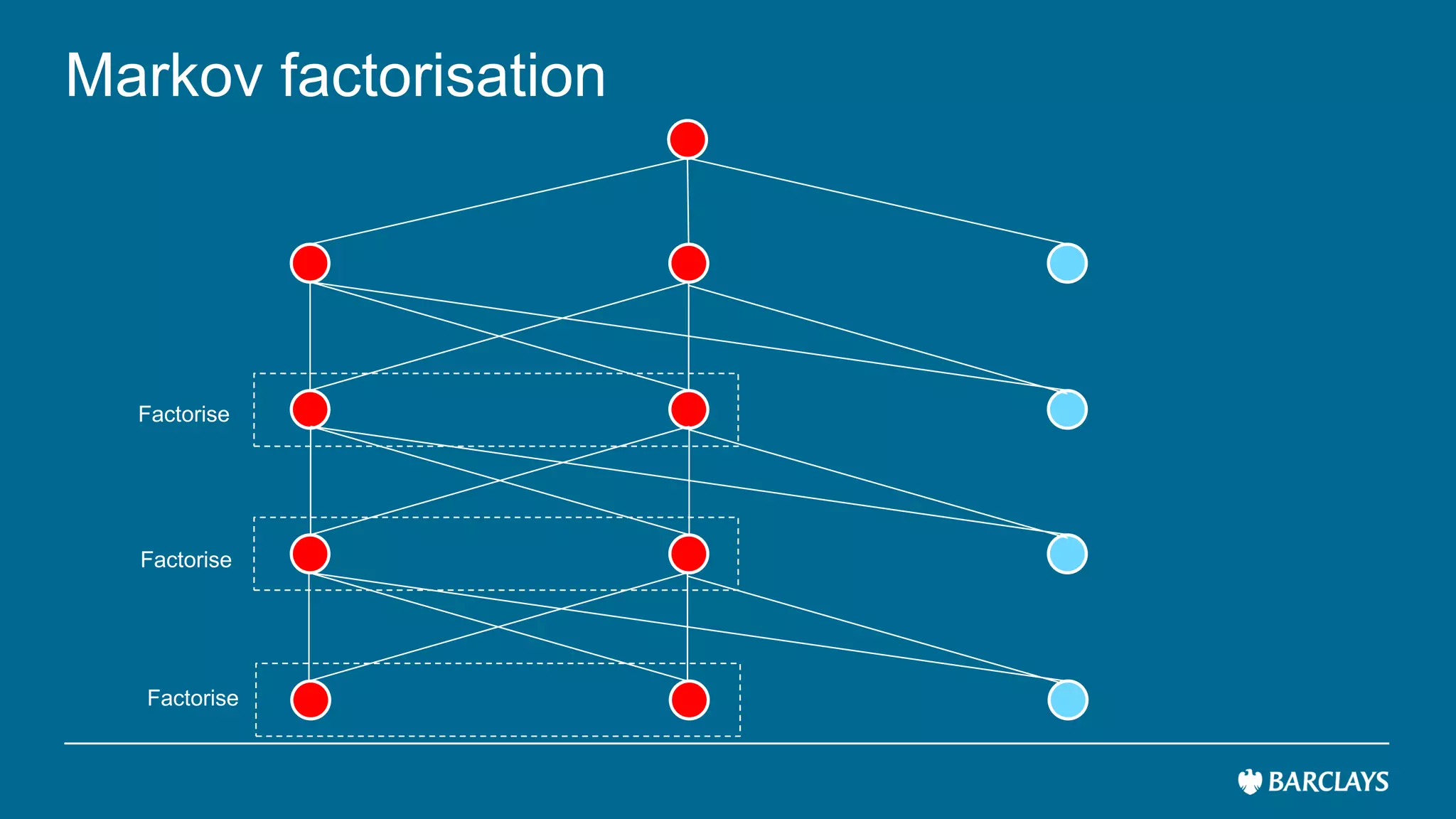
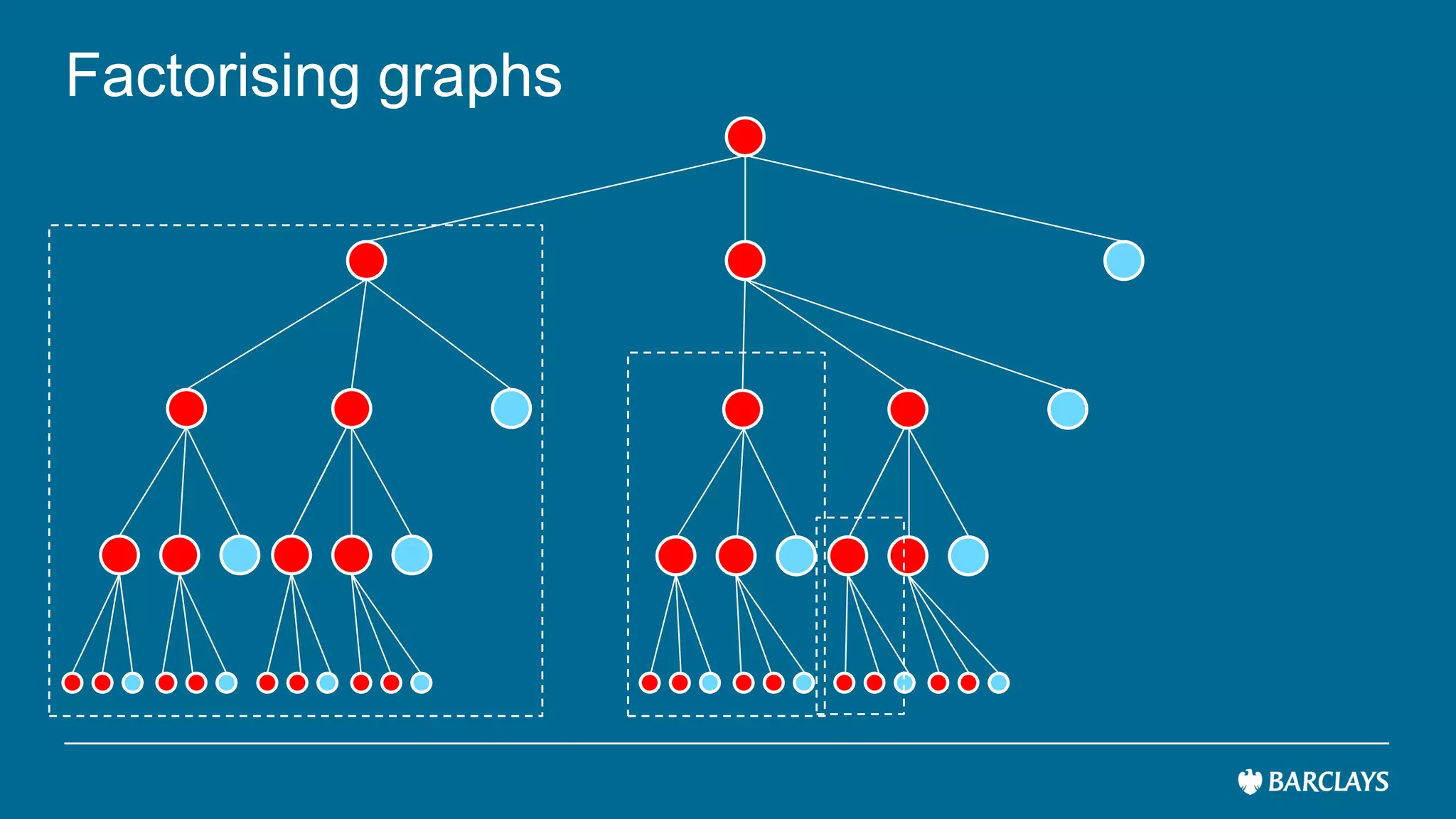
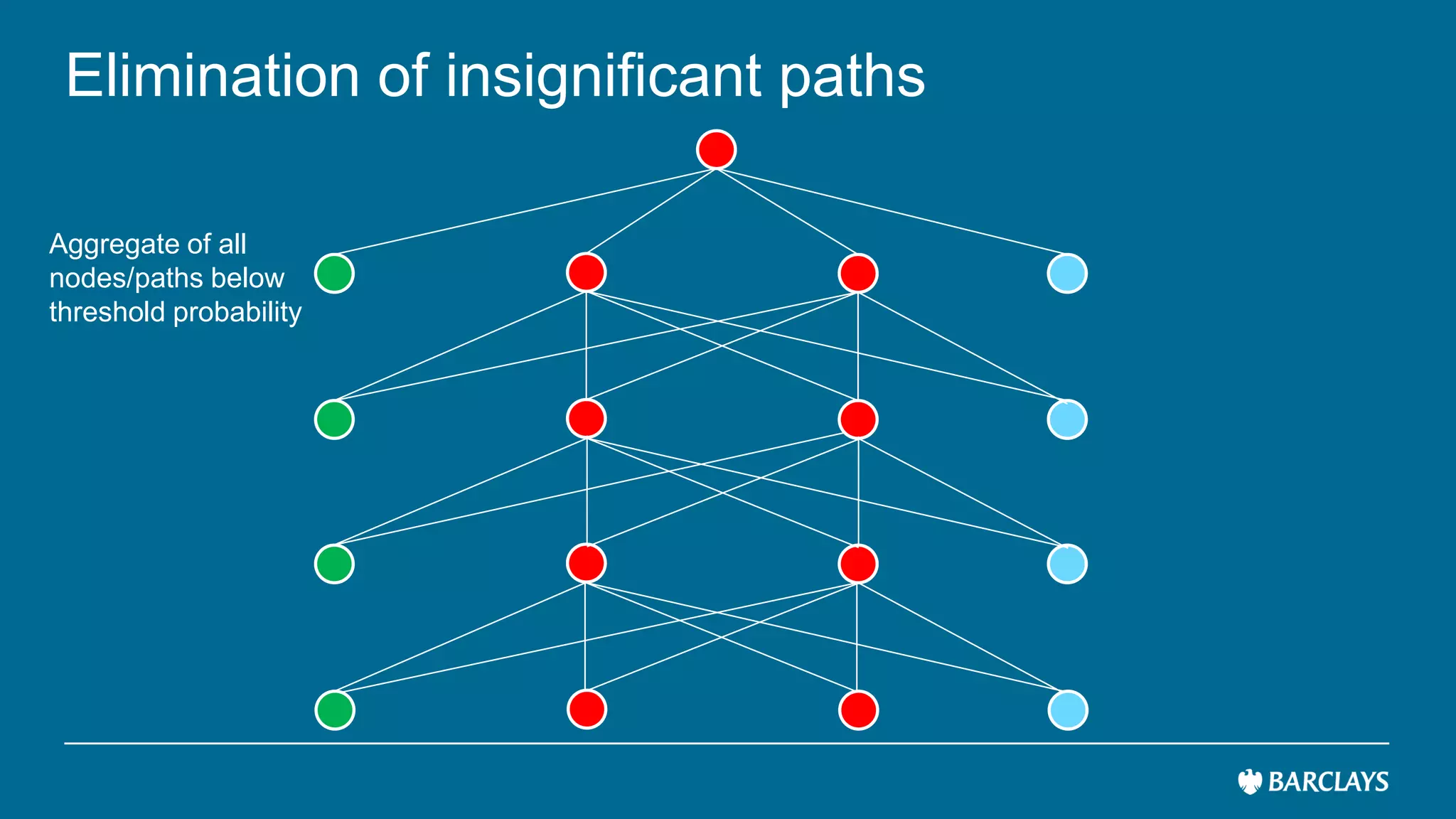
The document discusses the use of advanced data analytics to understand customer values and improve recommendation engines, highlighting the limitations of conventional similarity metrics in sparse and hub-centric networks. It reviews methods such as absorbing transition matrices and path sampling to estimate effective distances between businesses based on customer behavior, noting scalability challenges. The findings indicate that while probabilistic graph similarity metrics can enhance customer behavior characterization, further research is needed on their statistical properties and computational efficiency.

1. Graph Recommendations
Harry Powell & Raffael Strassnig
Advanced Data Analytics - Barclays

2. Customer values and recommendation engines
Understanding customer values is a similar problem to recommendation
– How is Tesco similar to Asda?
– How is Tesco in Bristol similar to Asda in Bath?
– How is Tesco in Bristol similar to Bristol Angling Centre?
Assume that the similarity of two businesses can be inferred by the extent
to which they share customers

3. The data: Customer transactions
Timestam
p
Customer Business Amount (£)
… Bob Smith Tesco, Bristol …
… Mary
Jones
Tesco, Bristol …
… Bob Smith Asda, Bath …
… John
Taylor
Bristol Angling Centre …

4. Transactional data can be seen as a bipartite
graph
Tesco
Asda BP
Boots
Timestam
p
CustomerI
D
MerchantName Amount (£)
… 1 Tesco …
… 1 Asda …
… 2 Boots …
… 2 BP …
… 3 Tesco …
… 3 Boots …
… 3 BP …
… 4 Asda …

5. Transactions imply customer preferences over
business values
Tesco

Price
Quality
Boots

Health
? Price ?
? Quality ?
Asda

Price
Customer
Business

6. Problems with conventional similarity metrics
Conventional recommenders (say Cosine similarity) are useless in
sparsely connected networks
𝐴𝑠𝑑𝑎 = 𝐀 = (1,1,1,0,1,1,0,0)
𝑇𝑒𝑠𝑐𝑜 = 𝐁 = 1,0,1,0,1,1,0,1
𝐀 ⋅ 𝐁 = 𝐀 𝐁 cos 𝜃
Customer Tesco Asda
Bob Smith Yes Yes
Mary Jones No Yes
John Taylor Yes Yes
Jane
Williams
No No
Gary Brown Yes Yes
Liz Davis Yes Yes
David Evans No No
Helen
Wilson
Yes No

7. Problems with conventional graph metrics
Conventional graph metrics (say minimum distance) are useless in
networks with significant hubs.

8. Inferring latent preferences from n-degree
separation
Tesco Boots Asda Lloyds
Pharmacy

9. Tesco
Asda
BP
Boots
Expected Degrees of Separation

10. Can factorise out to homogeneous graph
Tesco Asda BP BootsTesco
Asda BP
Boots
Tesco
Asda
BP
Boots
𝑝 𝐴 𝐵

11. Large number of paths
Each node has a few
thousand outgoing
edges
Destination
Business
a
d
aa
b c
bc d d

12. Markov factorisation
Factorise
Factorise
Factorise

13. Factorising graphs

14. Scalability problems with trees
Where 𝑛 = 1,000,000
Actually 𝑛 starts at a few thousand for low 𝑘, but quickly escalates
𝑛
𝑠𝑜𝑢𝑟𝑐𝑒
𝑛𝑜𝑑𝑒𝑠
× (𝑛 − 1)
𝑑𝑒𝑠𝑡𝑖𝑛𝑎𝑡𝑖𝑜𝑛
𝑛𝑜𝑑𝑒𝑠
× 𝑘
𝑑𝑒𝑝𝑡ℎ
× (𝑛 − 1)
𝑛𝑜𝑑𝑒𝑠 𝑎𝑡
𝑒𝑎𝑐ℎ 𝑠𝑡𝑒𝑝
⇒ 𝑂 𝑛3 𝑘

15. Elimination of insignificant paths
Aggregate of all
nodes/paths below
threshold probability

16. Comparing PageRank and Asymptotic EDS
PageRank: stationary distribution non-absorbing (eigenvector)
EDS: we would like to know how far we need to go (on average) to hit B
starting from A
Comment on ergodicity and teleporting
 Teleporting solely mechanism to get around non-ergodic graphs
 We assume a connected graph (eliminate graphs that only have
customers that solely shop with them) natural for retail not for websites.

17. Absorbing transition matrix
Discrete phase type distribution
– Computes EDS for all sources to single destination
– Gives exact results
𝑃 =
𝑇 𝑡
0 1
, 𝐸𝐷𝑆 = 𝐼 − 𝑇 −1

18. Spark implementation of Absorbing Transition
Matrix
[Spark code]
Has unacceptably high complexity (𝑂(𝑛4)) due to inverting large matrix

19. Estimating EDS using path sampling
An alternative is a sampling approach which is fully distributable
– Complexity = 𝑂(𝑛 × 𝑘 × 𝑙)
– Converges to analytical solution
Cautions
– Shorter path length can have high variance (𝑙 < 4)
– Signal dilution (applies to exact solution too)

20. Spark implementation of sampling methodology
Convergence fails when paths too long

21. Results

22. Results
MCDONALDS PRIMARK STORES LTD
PRIMARK STORES LTD 90.8 MCDONALDS 53.7
LIDL 105.3 LIDL 105.0
BOOTS 121.2 BOOTS 120.1
ALDI 123.2 ALDI 122.8
MARKS&SPENCER PLC 126.9 MARKS&SPENCER
PLC
126.2
POST OFFICE COUNTER 128.2 POST OFFICE
COUNTER
128.2
GREGGS PLC 154.1 GREGGS PLC 154.2

23. Results vs Pagerank
Pagerank EDS
SEVERN RIVER CROSSIN
PLC
MCDONALDS
MCDONALDS PRIMARK STORES LDT
POST OFFICE COUNTER LIDL
LIDL BOOTS
PRIMARK STORES ALDI
ALDI MARKS&SPENCER PLC
MARTIN MCCOLL POST OFFICE COUNTER
MARKS&SPENCER PLC GREGGS PLC

24. Results
Results aren’t much use because of low differentiation between shops
Once you have escaped vicinity of a shop reverts to random walk.
Certain nodes connect everything (MCDONALDS, IKEA)
Theoretically interesting metric – but not insightful

25. Localised EDS

26. Localised EDS
𝑃 =
𝑇 𝑡
0 1
We use that 𝑃 𝑘 which yields the results for the k-neighbourhood
Set k according to the problem at hand (eg. 5, 10, 20, …)

27. Spark implementation of Localised EDS

28. Brute force GPU implementation of Localised
EDS
Brute force matrix multiplication using GPUs
Parallelisation can be achieved by destination node
Sort-of scales (𝑂(𝑘 . 𝑛3
) ) as long as matrix fits into memory
Can be faster than Spark

29. Compare results from EDS and Localised EDS
STARBUCKS BS16
Starbucks BS 35 1.51 McDonalds 54.0
KFC 2.04 Primark Stores 90.9
Krispy Creme 3.11 Lidl 105.9
The Old Fish Market Pub 4.8 Boots 120.2
IKEA 6.74 Marks & Spencer 126.3

30. Summary
• We used a probabilistic graph similarity metric to derive a richer
characterisation of customer behaviour
• We implemented a number of approaches to estimate it
• All had complexity/scalability challenges
• Use it yourselves and share what you find!
Further work
• Derive the statistical properties of the EDS
• Explore methods for approximation of matrix multiplication

31. Data Science Section
….coming soon!