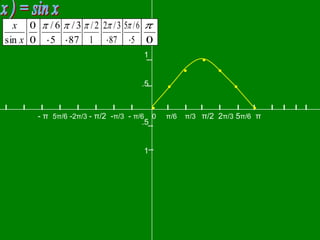
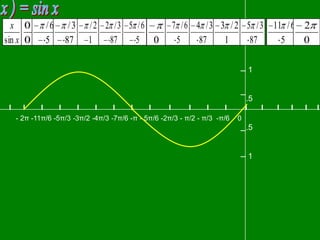
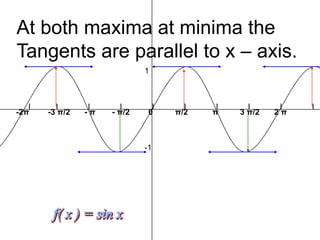
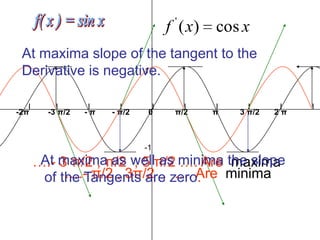
The document contains graphs of trigonometric functions such as sin(x), tan(x), and cot(x) with their domains and ranges. It also discusses properties of these functions including that they have: - Maxima and minima occurring at specific values of x where the derivative is zero and the tangent line is parallel to the x-axis. - The slope of the tangent line to the derivative is negative at maxima.

1. I
y = f ( x) = x y
I
I
I I I I I I I I I
x’
I
-4 -3 -2 -1 0 1 2 3 4
x
I
I
I
Y’
I

2. I
y = f ( x) = IxI y
I
I
I I I I I I I I I
I
x’ -4 -3 -2 -1 1 2 3 4
0 x
I
I
I
Y’
I

3. I
y
Y = f ( x) = 1/x
I
I
x’ I I I I I I I I I
I
-4 -3 -2 -1 0 1 2 3 4 x
I
I
I
Y’
I

4. I
y
Y = f ( x) =[ x ]
I
I
I I I I I I I I I
I
x’ -4 -3 -2 -1 1 2 3 4
0 x
I
I
I
Y’
I

5. I
y
I
I
I I I I I I I I I
x’
I
-4 -3 -2 -1 0 1 2 3 4
x
Y = f ( x) = x 2 I
I
I
Y’
I

6. x 0 / 6 / 3 /2 2 /3 5 /6
sin x 0 5 87 1 87 5 0
1
.5
I I I I I I I I I I I I I I I I I I
- π 5π/6 -2π/3 - π/2 -π/3 - π/6 0 π/6 π/3 π/2 2π/3 5π/6 π
.5
1

7. x 0 /6 /3 /2 2 /3 5 /6
sin x0 5 87 1 87 5 0
1
.5
I I I I I I I I I I I I I I I I I I
- π 5π/6 -2π/3 - π/2 -π/3 - π/6 0 π/6 π/3 π/2 2π/3 5π/6 π
.5
1

8. x 0 / 6 / 3 /2 2 /3 5 /6 7 / 6 4 / 3 3 / 2 5 / 3 11 / 6 2
sin x 0 5 87 1 87 5 0 5 87 1 87 5 0
1
I
I
.5
I I I I I I I I I I I I I I I I I I I
0 π/6 π/3 π/2 2π/3 5π/6 π 7π/6 4π/3 3π/2 5π/3 11π/6 2π
.5
I
1
I

9. x 0 /6 /3 /2 2 /3 5 /6 7 / 6 4 / 3 3 / 2 5 / 3 11 / 6 2
sin x 0 5 87 1 87 5 0 5 87 1 87 5 0
1
I
I
.5
I I I I I I I I I I I I I I I I I I I
- 2π -11π/6 -5π/3 -3π/2 -4π/3 -7π/6 -π - 5π/6 -2π/3 - π/2 - π/3 -π/6 0
.5
I
1
I

10. x 0 /6 /3 /2 2 /3 5 /6
sin x 1 87 5 0 5 87 1
1
.5
I I I I I I I I I I I I I I I I I I
- π 5π/6 -2π/3 - π/2 -π/3 - π/6 0 π/6 π/3 π/2 2π/3 5π/6 π
.5
1

11. x 0 /6 /3 /2 2 /3 5 /6
sin x 1 87 5 0 5 87 1
1
.5
I I I I I I I I I I I I I I I I I I
- π 5π/6 -2π/3 - π/2 -π/3 - π/6 0 π/6 π/3 π/2 2π/3 5π/6 π
.5
1

12. 1
I I I I I I I I I I
-2π -3 π/2 -π - π/2 0 π/2 π 3 π/2 2π
-1

13. x 0 / 6 / 3 /2 0 /2 0 2 /3 5 /6 7 / 6 4 / 3 3 / 2 0 3 / 2 0 5 / 3 11 / 6 2
tan x 0 58 1 73 1 73 58 0 58 1.73 1 73 58 0
1
I
I
.5
I I I I I I I I I I I I I I I I I I I
0 π/6 π/3 π/2 2π/3 5π/6 π 7π/6 4π/3 3π/2 5π/3 11π/6 2π 5π/2
.5
I
1
I

14. x 0
tan x 0
1
I
I
.5
I I I I I I I I I I
-2π -3 π/2 -π - π/2 0 π/2 π 3 π/2 2π
.5
I
1
I

15. x 0 /6 /3 /2 2 /3 5 / 6 0 0 7 / 6 4 / 3 3 / 2 5 / 3 11 / 6 2 0
cot x 1 73 58 0 58 1 73 1 73 .58 0 58 1 73
1
I
I
.5
I I I I I I I I I I I I I I I I I I I
0 π/6 π/3 π/2 2π/3 5π/6 π 7π/6 4π/3 3π/2 5π/3 11π/6 2π 5π/2
.5
I
1
I

16. 1
I
I
.5
I I I I I I I I I I
-2π -3 π/2 -π - π/2 0 π/2 π 3 π/2 2π
.5
I
1
I

17. -2π
I
Goes tp + infinity
I
-3 π/2
I
Goes tp + infinity
-π
Goes tp - infinity
I
- π/2
Goes tp - infinity
1
1
0
I
Goes tp + infinity
I
π/2
Goes tp + infinity
I
π
Goes tp - infinity
I
3 π/2
Goes tp - infinity
I
2π
I

18. Goes tp + infinity
-2π
II
Goes tp + infinity
-3 π/2
Goes tp - infinity
I
-π
Goes tp - infinity
I
- π/2
Goes tp + infinity
1
1
0
II
π/2
Goes tp + infinity
Goes tp - infinity
I
π
Goes tp - infinity Goes tp + infinity
I
3 π/2
I
2π
Goes tp + infinity
I

19. I
1
f ( x) sin x
I
I
I
I
I
I
I

20. I
y
f(x) = x
I
x
y e
I
I I I I I I I I I
I
x’ -4 -3 -2 -1 (1,0) 2 3 4
0 x
I
y log e x
I
I
Y’
I

21. I
y = f ( x) = x y
I
I
I I I I I I I I I
x’
I
-4 -3 -2 -1 0 1 2 3 4
x
When x increases f( x) also increases.
f(Y == x is=strictly increasing function
x) f( x) x is continuous function.
I
I
I
Y’
I

22. ….- 3 π/2 , π/2 , 5 π/2 …. Are maxima as at
these values of x ,f(x) is maximum.
1
I I I I I I I I I I
-2π -3 π/2 -π - π/2 0 π/2 π 3 π/2 2π 5π/2
-1
-

23. ….- π/2 , 3π/2 , …. are minima as at these
values of x, f(x) is minimum.
1
I I I I I I I I I I
-2π -3 π/2 -π - π/2 0 π/2 π 3 π/2 2π 5π/2
-1

24. At both maxima at minima the
Tangents are parallel to x – axis.
1
I I I I I I I I I I
-2π -3 π/2 -π - π/2 0 π/2 π 3 π/2 2π
-1

25. At both maxima at minima the Derivative
of the function is zero. Or f x 0
1
I I I I I I I I I I
-2π -3 π/2 -π - π/2 0 π/2 π 3 π/2 2π
f
-1

26. Slope of the tangent is zero of the tangent is zero
Slope
1
I I I I I I I I I I
-2π -3 π/2 -π - π/2 0 π/2 π 3 π/2 2π
-1
Slope of the tangent is zero

27. '
f ( x) cos x
At maxima slope of the tangent to the
Derivative is negative.
1
I I I I I I I I I I
-2π -3 π/2 -π - π/2 0 π/2 π 3 π/2 2π
-1
….- maxima as wellπ/2 minima the slope
At 3 π/2 , π/2 , 5 as …. Are maxima
….- π/2 , 3π/2 , …. Are minima
of the Tangents are zero.